基于软判决的(n,1,m)卷积码盲识别∗
2018-04-27蒋飘蓬
蒋飘蓬 刘 杰 马 超
(1.海军航空大学信息管理中心 烟台 264001)(2.海军航空大学信息融合研究所 烟台 264001)
1 引言
随着现代通信系统对图像、视频等数据传输需求的提升,信道编码技术得到了广泛的应用。在智能通信和通信对抗领域,为恢复原始信号,就必须先掌握对应的编码参数和传输协议。因此,信道编码盲识别技术迅速成为一个新的研究热点,并取得了丰硕的研究成果[1~2]。
(n,1,m) 卷积码是无线通信、卫星通信和深空通信等领域常见的一种编码方式,具有编码模型简单、纠错性能优良等特点。根据目前已公开发表的文献,常见的卷积码识别方法主要有基于矩阵分析的方法[3~6]、欧几里得算法[7~8]和基于沃尔什-阿达玛变换(Walsh-Hadamard Transform,WHT)的方法[9~10]。上述方法都基于解调后的硬判决0、1比特序列,在误码率较高时性能往往会受到限制。如果解调时匹配滤波器采用软判决,则由于输出没有经过量化,不仅能通过后续处理得到硬判决比特序列,还能获得每位比特对应的可靠性信息。
2 问题分析与识别模型
2.1 (n ,1,m )卷积码编码原理
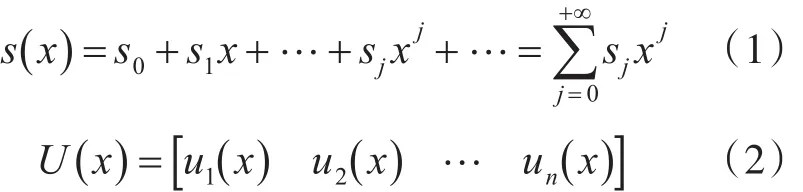
其中

设生成多项式矩阵为
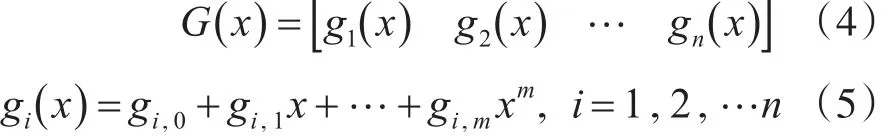
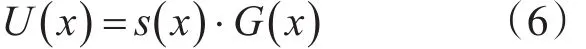
对应编码结构如图1所示,其中⊕表示二元域加法,⊗表示二元域加法,D表示移位寄存器。

图1 (n,1,m)卷积码编码结构
2.2 识别模型
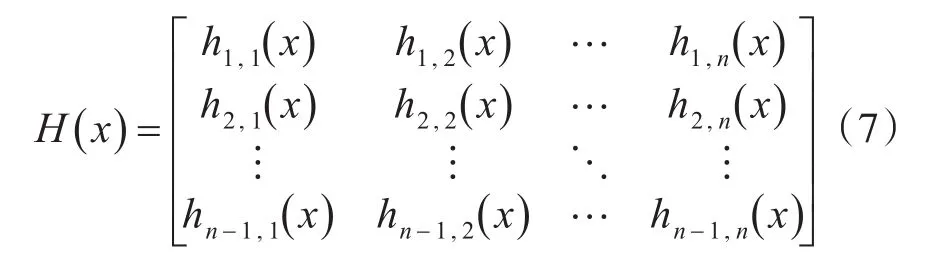
其中,
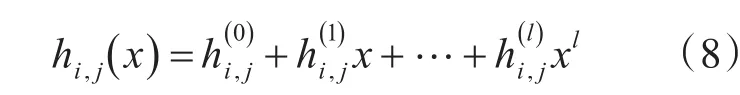
根据校验关系,有

式中,符号T表示转置,0表示零向量。联立式(6)和(9)得

根据表2中数据可知,当阳离子试剂与CHSOS的物质的量比低时,CHSOS的环氧值较大,CHSOS的产率较低,随着物质的量比增加,CHSOS的产率逐渐升高。由表2可明显看到,当阳离子试剂与CHSOS的物质的量比在0.9∶1~1.2∶1时,CHSOS的产率逐渐升高。当物质的量比大于 1.2∶1后,CHSOS的产率却降低。这是因为产物中除了CHSOS之外,还会产生大量三甲胺盐酸盐副产物,较难分离[20]。因此本实验选择阳离子试剂与ESESO的物质的量比为1.2∶1。
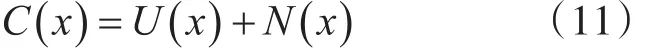
相应的,有
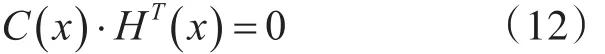
3 基于软判决的识别方法
由式(12)可得
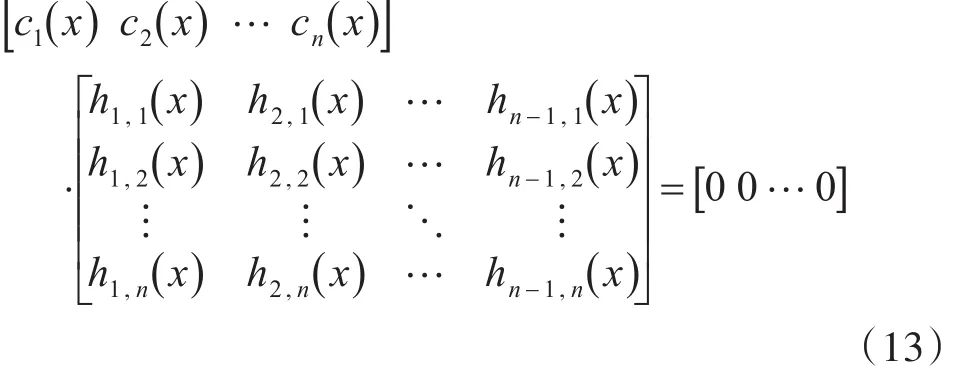
上式实际由n-1个方程构成,每个方程中包含个未知数。由于每个方程的系数均相同,因此只对其中一个研究即可,且其必然包含多组解。据此,有


其 中 ,,j和i,j分 别 表 示cr和hi中 第个元素。令


则Yi值越大,成立的概率越大,对应hi越可能是式(14)的解。因此,定义Yi为hi的符合度。根据文献[12]:

其中

假设调制方式为BPSK,传输信道为AWGN信道。设发送的二元信息序列为,对应信号经解调得到的软判决序列为,则
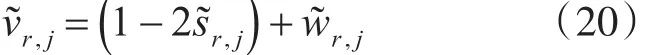
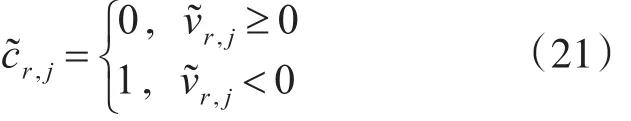
则与此硬判决相关的对数似然比(Log Likeli⁃hood Ratio,LLR)可表示为
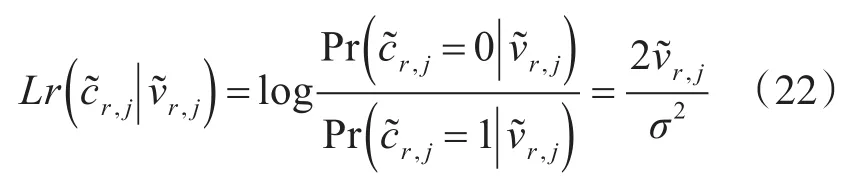
又

于是,



上式整理后左侧是一个包含未知数的多项式,令其所有系数为零,就可求得所有的系数,进而得到生成多项式矩阵。
4 仿真验证与性能分析
4.1 仿真验证

图2 校验向量识别结果
可以看出,极大值有7个,对应的校验向量分别为(000011100011),(011100011000),(01111111 1011),(101001000110),(101010100101),(1101010 11110),(110110111101)。按式(26)建立方程,有:

4.2 性能分析
下面分析不同参数下的识别性能。首先固定存储级数m=5,在码长n分别为2、3和4的情况下,识别概率随信噪比的变换曲线如图3所示;然后固定码长n=5,在存储级数m分别为3、4和5的情况下,识别概率随信噪比的变换曲线如图4所示。可以看出,在相同信噪比下,编码参数越大,识别概率越低,与实际相符。在信噪比大于2dB时,本文方法对仿真所采用的各种编码方式均能达到100%的识别概率。
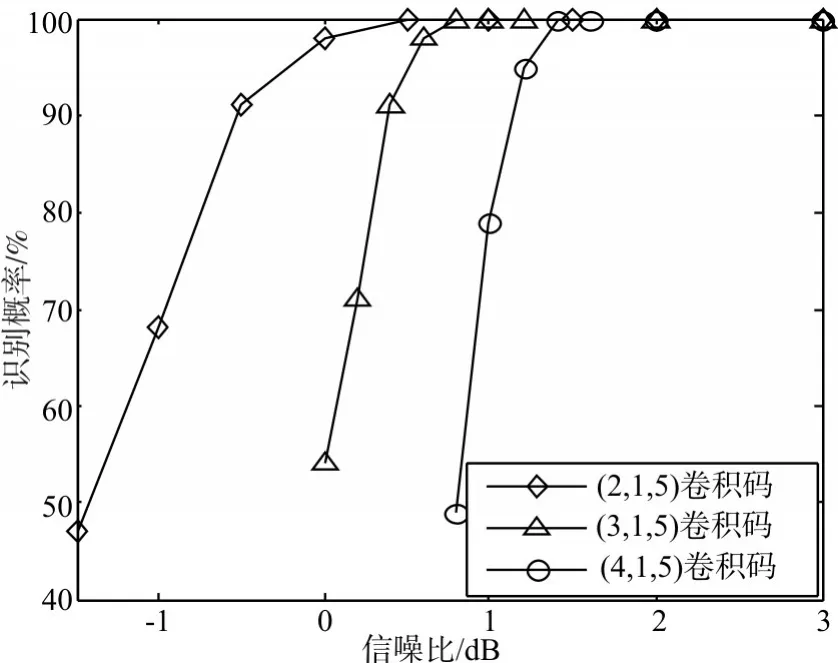
图3 不同码长下的识别结果
5 结语
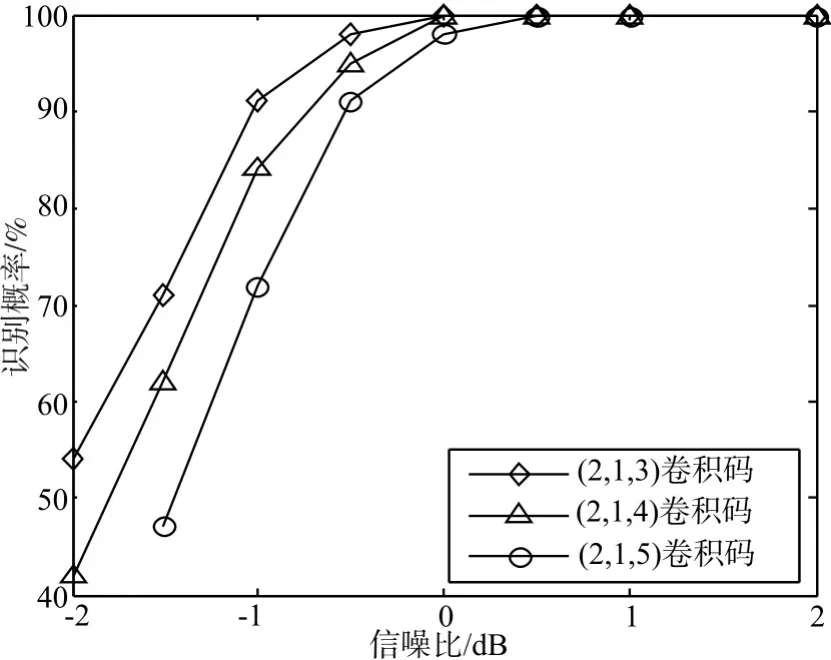
图4 不同存储级数下的识别结果
[1]YU Peidong,PENG Hua,and LI Jing.On blind recogni⁃tion of channel codes within a candidate set[J].IEEE Communications Letters,2016,20(4):736-739.
[2]MOOSAVI R and LARSSON E G.Fast blind recognition of channel codes[J].IEEE Transactions on Communica⁃tions,2014,62(5):1393-1405.
[3]薛国庆,常逢佳,柳卫平,等.1/n卷积码盲识别[J].无线通信技术,2009,18(3):38-42.
[4]王翼,汪立新.一种卷积码的盲识别技术研究[J].计算机安全,2012(10):20-22.
[5]刘建成,杨晓静.基于求解校验序列的(n,1,m)卷积码盲 识 别[J]. 电 子 与 信 息 学 报 , 2012,34(10):2363-2368.
[6]杨晓静,刘建成,张玉.基于求解校验序列的(n,k,m)卷积码盲识别[J].宇航学报,2013,34(4):568-573.
[7]刘建成,杨晓静,张玉.基于改进欧几里德算法的(n,1,m)卷积码识别[J].探测与控制学报,34(1),2012:64-68.
[8]解辉,王丰华,黄知涛,等.基于改进欧几里得算法的卷积码快速盲识别算法[J].国防科技大学学报,2012,34(6):158-162.
[9]刘健,王晓军,周希元.基于Walsh-Hadamard变换的卷积码盲识别[J]. 电子信息学报,2010,32(4):884-888.
[10]张岱,张玉,杨晓静,等.基于分段抽取软判决加权Walsh Hadamard变换的卷积码识别算法[J].兵工学报,2015,36(12):2298-2305.
[11]王新梅,肖国镇.纠错码原理与方法[M].西安:西安电子科技大学出版社,2011:378-415.
[12]刘骏,李静,彭华.基于校验方程平均符合度的Turbo码 交 织 器 估 计[J].电 子 学 报 ,44(5),2016:1213-1218.
