基于改进自适应Kalman滤波的地铁变形监测研究∗

钟 昆 高 嵩 黄姣茹

（西安工业大学自主系统与智能控制国际联合研究中心 西安 710021）

1 引言

鉴于涌入城市的人口数量逐年攀升，大力兴建城市地下铁路交通运行网，成为解决交通拥堵和市民出行难的一剂良方。然而，地铁普遍位于城市的繁华中心地段，加上地面建筑物和地下管线等地质条件会加重地铁隧道的自身负荷，导致隧道结构出现裂缝和沉降等形变，若不及时监测与修复，将会造成地面塌方甚至危及人身安全［1］。因此，对地铁隧道结构进行实时的、连续的、长期的变形监测便成为当前刻不容缓的任务［2］。

目前，地铁变形监测技术已经由传统的依靠人力与仪器监测转变为如今先进的智能全站仪（测量机器人）的自动化监测技术［3］，可以实现全自动观测并采集数据。由于可变因素影响，变形监测数据通常会包含各种误差与形变信息，仅从数据的表面，无法反映真实的信息。因此，如何及时有效地从繁多的变形监测信息中进行数据挖掘，提取关键性数据，并对此时变形情况进行合理分析的问题成为了关键［4］。

近年来，许多学者通过研究变形监测数据序列的结构与规律，建立动态模型来反映变形特征并推断变化趋势。文献［5］通过建立时间序列模型来近似模拟动态数据以达到预测的目的。但是该方法需要不断地根据新的观测数据建立新模型来求得结果，并且没有考虑观测数据含随机扰动的情况。文献［6］采用了灰色系统理论对监测数据进行建模分析，利用预测模型GM（1，1）［7］在一定程度上修正了传统模型的偏差。但仿真发现当观测结果含有随机扰动误差时，预测结果质量会降低。文献［5，6］虽能精准建立数据的动态模型，但均未解决监测数据存在随机噪声扰动的问题。文献［8］选用卡尔曼滤波算法［9］对监测数据进行滤波处理，有效剔除了随机扰动误差的影响。但是在采用卡尔曼滤波算法前，须了解系统噪声的先验知识以及对初始状态和方差的准确给定，否则会出现滤波发散［10］，导致决策者对变形监测趋势作出误判。文献［11］提出用自适应卡尔曼滤波［12］来解决，利用方差补偿的原理克服了由于噪声统计模型不准确而产生的滤波发散现象。但是会出现估计值发生振荡且收敛速度缓慢的现象，并不能达到理想效果。文献［8，11］虽能降低随机噪声的影响，但存在收敛速度慢甚至发散的现象，不能更好地应用在工程当中。

因此，本文提出一种改进自适应卡尔曼滤波算法，通过在一步预测方差阵的计算式中引入指数型衰减因子［13］，利用残差序列保持正交的特性推导出幂值表达式进行计算，不仅削弱了随机扰动噪声对估计的影响，而且克服了传统自适应卡尔曼滤波算法收敛速度缓慢甚至发散的现象。同时，极大程度上提高了利用该改进算法后得到的最优估计值的精确性与稳定性。

2 监测系统模型

由智能全站仪组成的地铁变形监测系统在获取监测点的初始位置信息后，能够自动完成数据采集、数据传输、数据处理、自动预警和成果输出等工作。全站仪具有自动测边和测角的能力，一台全站仪，采用极坐标测量法［14］就可获得被测点的二维坐标或者三维坐标，极坐标测量法示意图如图1。

如图1所示，以全站仪的设站点o点为原点，测站的铅垂线为z轴，以定向方向为x轴，建立左手直角坐标系o-xyz。设全站仪测量点的观测值分别为：水平角α，垂直角β，斜距S，则P点所示的测站坐标为

由此，可以通过独立坐标系下的坐标公式（1）计算出监测点的x方向的位置x(k)和y方向的位置y(k)。

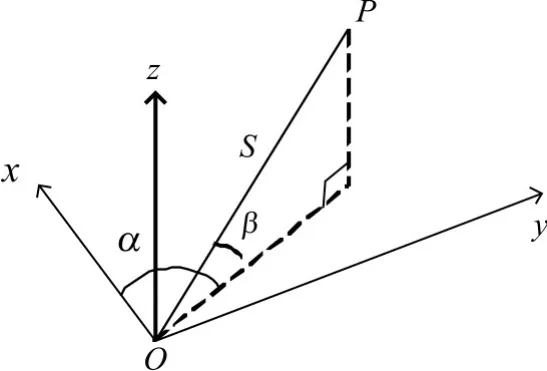
图1 极坐标测量法示意图

现在，面临的问题是如何根据采集到的原始数据进行处理，进而对变形体进行预报分析。常用的监测系统模型建立方法主要有常加速度模型、常速度模型以及随机游走模型［15］。本文选择常速度模型作为状态方程，随机游走模型作为观测方程。方法如下。

常速度模型是监测点的位移关于时间的一阶泰勒系数展开式，假设监测点的变形量近似看成典型的运动模型，只把变形的位移和速率作为状态参数，将监测点位移变化的加速率作为随机干扰项。由以下运动公式得到：

式中：由极坐标测量法得到变形监测点的位置，其运动状态包括X方向的位置x(k)、Y方向的位置y(k)、X方向的速度vx(k)和Y方向的速度vy(k)，T为采样时间，监测点位移变化的加速率w(k)作为随机扰动量。得到变形监测模型的状态方程为

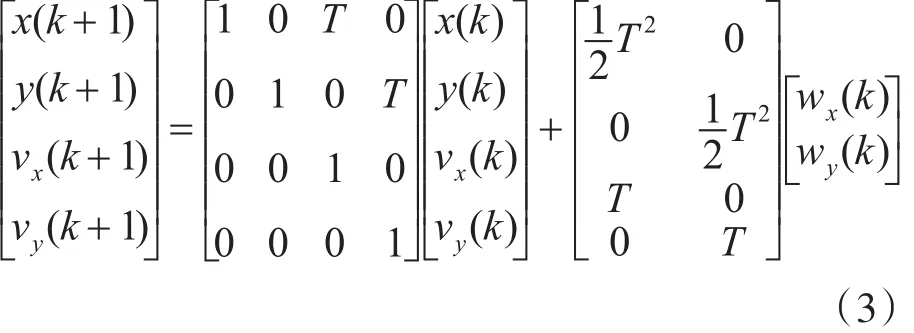
随机游走模型是仅考虑监测点的位置量，得到变形监测模型的观测方程为

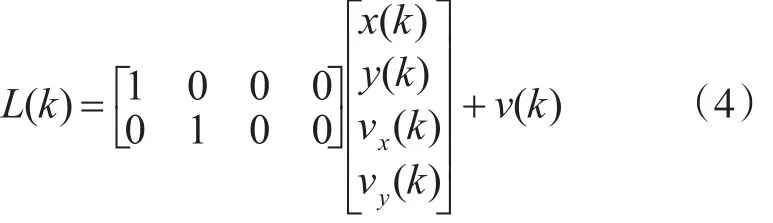
式中：L(k)表示第k期的观测值；v(k)表示观测系统噪声，包含了监测点的位移变化速率和加速率。

通过监测系统模型分析，得到状态方程式（3）与观测方程式（4），建立如下的系统模型［16～18］：

式中：k=1，2，3，…，N+；Xk-1、Xk分别为第k-1期、第k期的状态向量，Φk，k-1为第k-1期到第k期的状态转移矩阵，即

Ωk-1为第k-1期的系统动态噪声向量，即Ωk-1=w(k)，Γk-1为第k-1期动态噪声系数矩阵，即

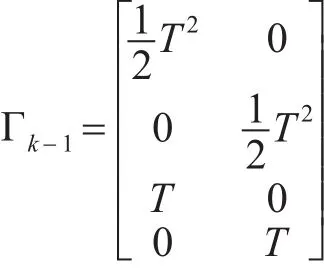
Lk为第k期的观测向量，Bk为第k期的观测向量系数矩阵，即，Δk为第k期的观测噪声向量，即Δk=v(k)。

对系统（5），当动态噪声和观测噪声服从高斯分布且统计特性已知时，采用经典卡尔曼滤波算法进行最优状态估计处理，得到的结果虽不能确切求出系统的真实状态，但是能够比用传统测量仪器测得的数据更加逼近于真实值；当噪声的统计特性不能准确给出且与实际有偏差时，则采用自适应卡尔曼滤波算法，可以对动态噪声协方差阵实时修正，降低偏差。但该方法在实际滤波中会出现收敛速度慢甚至发散的现象，本文提出的改进自适应卡尔曼滤波算法可以比传统算法更精准、更稳定地得出真实状态。

3 改进自适应卡尔曼滤波算法

自适应卡尔曼滤波算法主要特点在于能够在滤波过程中及时修正由于噪声或者模型参数不确定时的影响，其基本方程如下。

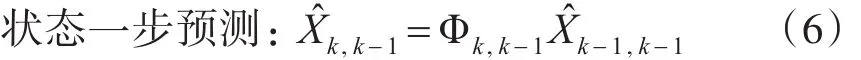
一步预测误差方差阵：

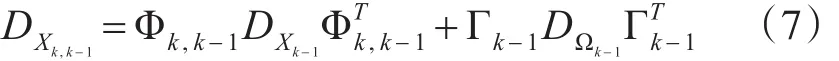
滤波增益矩阵：

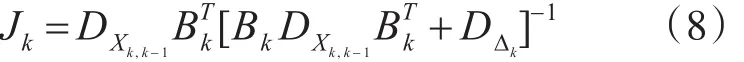
状态最优估计：

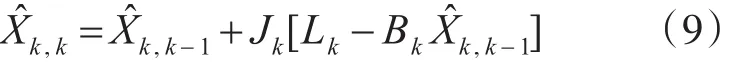
状态最优估计的误差方差阵：

动态噪声协方差阵估计：

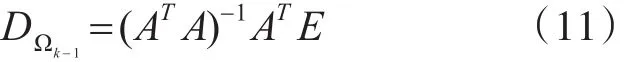
式（11）中：

其中，Lk表示为第k期的观测向量，为第k期的最佳预测值。推导过程在文献［11］中已详细列出。

然而，自适应卡尔曼滤波算法在实际工程应用中会出现收敛速度慢甚至发散的现象，本文在传统算法的基础上进行改进，对一步预测方差阵计算式（7）中增加一个指数型衰减因子，即

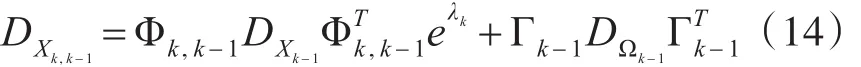
定理1 对于系统模型式（5），若采用如式（14）的含衰减因子的一步预测误差方差阵，则该系统具有抑制滤波发散特性的幂值满足下式：

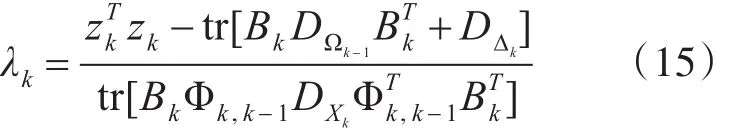
证明 首先，引入zk为残差序列（新息序列），且为高斯白序列，表达式为

得到协方差阵为

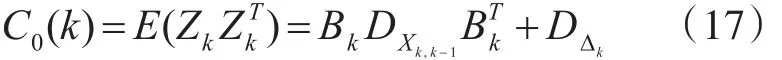
残差的自动协方差阵为

将式（8）和式（17）一并代入到式（18）中，得到

由此说明，当增益矩阵Jk为最优增益阵时，残差序列不相关，即残差序列处处保持正交。但是，由于模型存在误差，实际的残差协方差阵C0(k)与理论值存在差异。因此，Cj(k)不一定等于零。由式（18）可见，最后一项是共同项，若

则Jk是最优的，即：如果在线调整增益阵，迫使残差序列保持相互正交，那么式（20）成立。因此，定义：

则S(k)的最优值由下式决定：

式中：Sij(k)为S(k)的第i行第j列元素，f的值越小，滤波越接近最优。

根据发散判据：

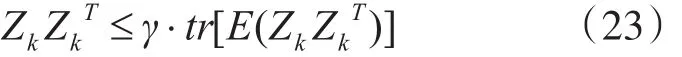
式中：γ为储备系数（γ＞1），当γ=1时是最严格的收敛判据条件。

采取严格的收敛判据条件，即

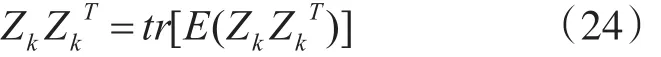
把式（14）和式（17）代入，并考虑λk是变量，得到：

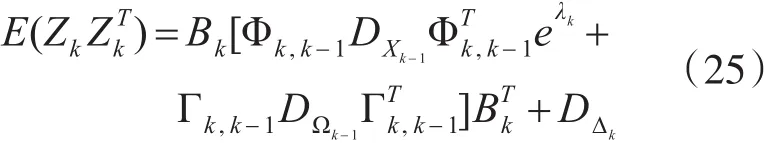
则抑制滤波发散的衰减因子为

证毕。

当加入了由定理1的幂值表达式得到的衰减因子后，通过在线调整滤波增益阵使其达到最优，再结合自适应卡尔曼滤波算法自身对动态噪声协方差阵实时修正的优势，使得不仅加快收敛速度和解决随机噪声对估计的影响，而且还提高了精确性和稳定性，这在接下来的应用仿真中得到证明。

4 应用仿真

针对某市在营运期间的某条地下铁路交通运输隧道中，利用监测设备对变形体进行监测工作，其中每隔两周对监测点进行一次数据记录，得到如下表1和表2中共10期的观测数据。现利用前文所述的监测系统模型式（5）建立离散型卡尔曼滤波模型，进行如下的仿真分析：

设变形监测点在X方向上和Y方向上的初始位置为 [x(0)，y(0)]T=[54.45，3.154]T，初始状态的误差方差阵，观测噪声初始方差，系统噪声初始方差（对于变形监测周期短的系统通常取噪声初始方差为单位阵），采样时间T为2。状态转移矩阵为，系统噪声的系数矩阵，观测向量的系数矩阵，其中I2表示为2阶的单位阵，02表示为2阶的零矩阵。根据以上值，对10期监测所得到数据分别进行经典卡尔曼滤波、自适应卡尔曼滤波和改进自适应卡尔曼滤波算法进行仿真计算［19-20］，结果见表1和表2。

其步骤可总结如下：

1）确定初始状态向量初值X(0)与Y(0)；

2）确定监测系统模型式（5）中的参数值及各系数矩阵常量；

3）利用改进自适应卡尔曼滤波算法计算公式［式（6）、式（8）～式（13）、式（14）、式（15）］进行最优滤波估计计算；

4）若估计值满足给定精度要求，退出滤波迭代过程，否则返回执行第3）步。

根据表1和表2的数据可以明显看出应用了改进自适应卡尔曼滤波算法得到的滤波值能够明显比其他两种算法更加接近于真实值。接下来，将表1和表2中的滤波值绘制成曲线图，分别如图2和图3所示，定量地比较三种滤波方法的效果。

从图2和图3看出，经典卡尔曼滤波结果在递推过程中与实测值的偏差越来越大，自适应卡尔曼滤波结果会在实测值附近不断产生振荡且速度缓慢。而含衰减因子的自适应卡尔曼滤波已显著的逼近实测值，并且随着时间的积累，没有出现明显的发散现象和振荡现象。

为了更加直观地比较三种滤波方法的精度和处理效果，绘制如图4和图5所示的误差分析图，定性地比较三种滤波方法的效果。

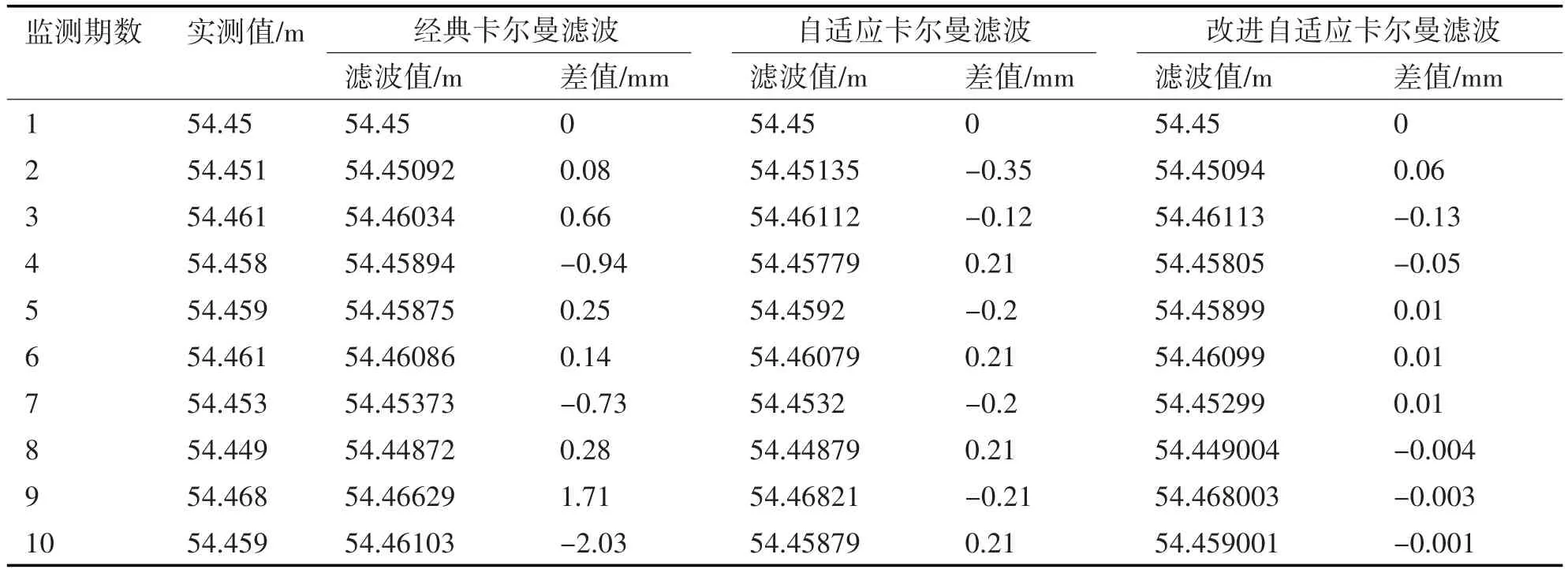
表1 监测点在X方向上的滤波值与实测值比较

表2 监测点在Y方向上的滤波值与实测值比较

图2 x方向上三种滤波方法的滤波值

图3 y方向上三种滤波方法的滤波值

由图4和图5明显看出，经典卡尔曼滤波在数据处理过程中所带来的偏差较大且不稳定，而改进自适应卡尔曼滤波方法收敛速度最快，并且能够精确地接近真实状态。图4中，经典卡尔曼滤波算法虽然在前8期数据之前误差都可以稳定在1个单位的误差范围，但在第9和第10期数据中，开始出现明显的发散现象，并且误差呈现增大的趋势，这在图5中也出现了相似的情况。在采用自适应卡尔曼滤波算法进行处理时，通过图4和图5看出，滤波效果有了很明显的改善，并且滤波值与实测值的误差逐渐缩小，能够稳定在0.5个单位的误差范围内，很好地解决了经典卡尔曼滤波法由于对系统模型不准确带来的滤波发散的问题，但滤波偏差值却出现了振荡现象，趋近于实测值的速度变慢了。

反观使用改进自适应卡尔曼滤波算法计算的误差，在前5期数据误差就已经降到0.3个单位的误差范围，之后偏差很快逼近于实测值，且整体变化平稳，收敛速度非常快。由此，验证了本文所述方法的有效性，在变形监测中达到了非常好的效果，其收敛速度和滤波精度都优于经典卡尔曼滤波算法和自适应卡尔曼滤波算法。

图4 x方向上三种滤波方法的误差对比

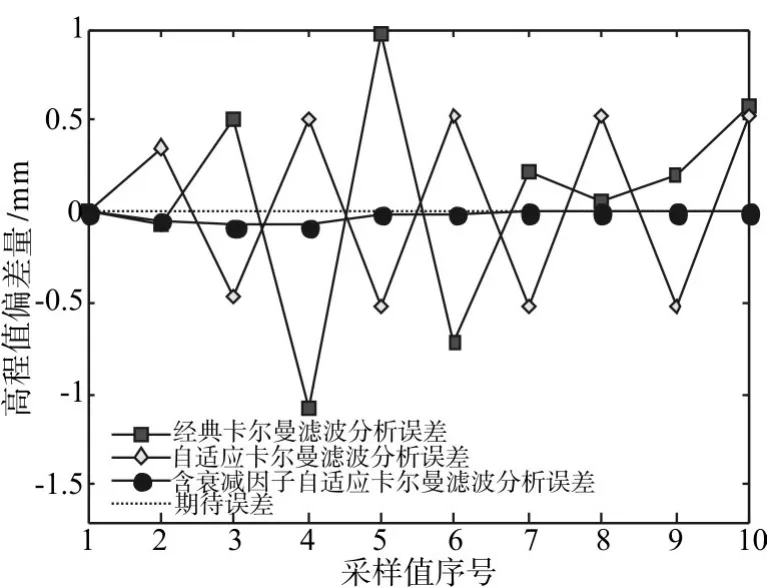
图5 y方向上三种滤波方法的误差对比

5 结语

针对地铁变形监测问题，考虑到自适应卡尔曼滤波算法出现收敛速度缓慢甚至发散的现象，本文在传统方法的基础上进行改进，引入指数型衰减因子，从而降低陈旧测量值对估计的影响，将推导出的衰减因子幂值表达式应用到改进算法中进行Matlab仿真。结果表明，相比较于未改进的算法，该方法能够较好地用来处理动态变形监测数据，具有收敛速度快、精度高、可靠性好等优势。

［1］LIU S T，YANG X M，LIANG Y B，et al.Applications of multimedia technology in deformation monitoring of sub⁃way tunnel［C］//IEEE Second International Conference on Multimedia and Information Technology，2010：47-50.

［2］BAI G B，ZHAO J，LIU L S.Deformation monitoring and data analysis for metro construction with mining method in Dalian［J］.Applied Mechanics&Materials，2013，356（3336）：1604-1608.

［3］刘绍堂，王果，潘洁晨.测量机器人隧道变形自动监测系统的研究进展［J］.测绘工程，2016，25（10）：42-48.

［4］ZHOU H M，HU J X，LIU X，et al.Ground deformation monitoring of Shenzhen metro area with Interferometric Point Target Analysis［C］//IEEE International Conference on Geoinformatics，2012：1-5.

［5］谢文国，高俊强，徐东风.时间序列在地铁隧道变形监测数据处理中的应用［J］.交通科技与经济，2015，17（4）：114-116.

［6］姜刚，杨志强，张贵刚.卡尔曼滤波算法的灰色理论模型在变形监测中的应用［J］.测绘科学，2011，36（4）：19-21.

［7］崔立志，刘思峰.基于数据变换技术的灰色预测模型［J］.系统工程，2010，28（5）：104-107.

［8］陈大勇，刘大伟.卡尔曼滤波法在城际高铁沉降变形监测与分析的应用［J］.测绘与空间地理信息，2015，38（6）：183-185.

［9］SU J Y，LI B B，CHEN W H.On existence，optimality and asymptotic stability of the Kalman filter with partially observed inputs［J］.Automatica，2015（53）：149-154.

［10］杨丹，曾以成，陈莉.抑制Kalman滤波发散的研究进展［J］.计算机工程与应用，2016，52（4）：13-18.

［11］王井利，张春哲.自适应卡尔曼滤波在地铁监测中的应用［J］.沈阳建筑大学学报（自然科学版），2014，30（2）：263-268.

［12］MAJA K，HU X M.An optimization approach to adap⁃tive Kalman filtering［J］.Automatica，2011（47）：1785-1793.

［13］夏启军，孙优贤.渐消卡尔曼滤波器的最佳自适应算法及其应用［J］.自动化学报，1990，16（3）：210-216.

［14］刘运明.自动极坐标实时差分监测技术在地铁隧道结构变形监测中的应用［J］.测绘通报，2016（1）：99-103.

［15］杜琨.变形监测数据处理的方法研究［D］.长沙：中南大学，2013：13-17.

［16］ZHANG W，FAN D L，YANG J Z.Adaptive Kalman fil⁃tering method to the data processing of GPS deformation monitoring［C］//IEEE Computer Society，International Forum on Information Technology and Applications，2010：288-292.

［17］潘娅，王姮，王牛.基于卡尔曼滤波的双闭环直流电机系统状态观测器［J］，信息与控制，2009，38（1）：15-23.

［18］GHALEB F A，ZAINAL A，RASSAM M，et al.Im⁃proved vehicle positioning algorithm using enhanced in⁃novation-based adaptive Kalman filter［J］.Pervasive&Mobile Computing，2017（40）：139-155.

［19］王志贤.最优状态估计与系统辨识［M］.西安：西北工业大学出版社，2004：109-112.

［20］黄小平，王岩.卡尔曼滤波原理及应用——Matlab仿真［M］.北京：电子工业出版社，2015：30-54.