基于PHD滤波的多目标跟踪及应用研究∗
2018-04-27齐海明张安清
齐海明 张安清
(1.海军大连舰艇学院研究生管理大队 大连 116018)(2.海军91202部队 葫芦岛 125004)(3.海军大连舰艇学院信息作战系 大连 116018)
1 引言
传统的多目标跟踪是通过数据关联技术来完成观测数据与目标间的分配,再通过滤波技术实现目标状态估计。典型的数据关联目标跟踪算法,如最近邻、联合概率数据关联以及多假设跟踪,这些算法主要存在两方面问题,一是核心过程数据关联运算时,随着目标数目增多,存在组合爆炸、计算量呈指数型增长等问题[1];二是进行多目标跟踪时,通常假设目标数目不变,而现实常常并不满足这个条件。
目前,Mahler提出的基于随机有限集(Random Finite Set,RFS)理论的多目标跟踪方法,因其能够有效避免传统数据关联存在的诸多问题,同时可以实现可变目标数的估计,已成为多目标跟踪技术发展的热门领域。2003年,Mahler首次提出了标准的PHD滤波,该方法具有坚实的数学基础,能更好反应目标跟踪问题的本质,在复杂的多目标跟踪中具有更小的计算复杂度,受到很多学者和工程技术人员的关注。
本文在回顾和介绍当前基于PHD滤波的多目标跟踪方法的研究现状与应用进展基础上,对未来该领域发展的几个重点方向提出了自己的设想。
2PHD滤波器
2.1 PHD滤波基本原理
PHD滤波算法实际是一种对后验多目标状态的一阶矩递推过程[2],由于其概率密度函数的积分步骤是在单个目标的运动状态上完成的,具有较小的运算量,相对Bayes滤波算法更容易处理。PHD滤波处理过程与传统Bayes滤波一样,也分为预测步和更新步,其核心思想流程如下[3]:
PHD滤波的预测方程为
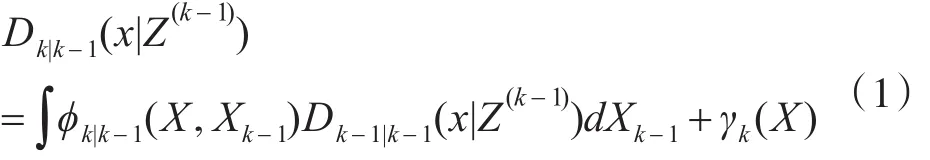
其中,ϕk|k-1(x,ξ)=bk|k-1(x|ξ)+ek|k-1(ξ)fk|k-1(x|ξ),这里,bk|k-1(·|ξ)表示衍生目标集Bk|k-1({ξ})的 PHD,ek|k-1(·)表示目标存在的概率,fk|k-1(·|·)表示单目标转移概率密度,γk(·)表示新生目标集Γk的PHD。
PHD滤波的更新方程为
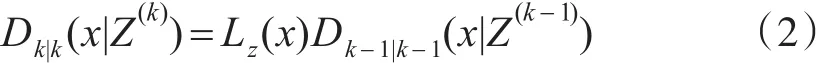
其中:
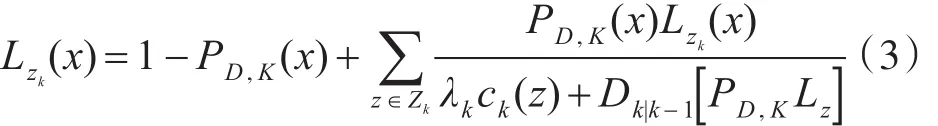
Lzk(x)表示单目标的观测似然函数,λk表示杂波强度,ck(z)表示杂波空间分布,λkck(z)表示杂波随机集的PHD。
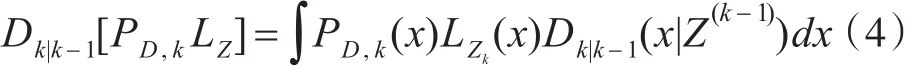
其中PD,k(·)表示检测概率。
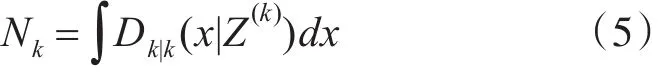
将最接近Nk的整数值作为k时刻的目标数的期望值,其目标数目估计值可表式为:峰值个数即表示目标个数。
2.2 PHD滤波器实现方法
PHD滤波更新过程中存在着复杂的积分运算,限制了PHD滤波的推广和应用。目前主要有两种实现方法,一是序贯蒙特卡洛法,即粒子滤波方法[2],Vo利用序贯蒙特卡洛法产生带有权值的随机粒子集,以粒子分布信息对PHD近似,提出序贯蒙特 卡 洛 PHD(SequentialMonteCarloPHD,SM-PHD)滤波算法,该算法优点是可以处理非线性非高斯问题,但同粒子滤波一样存在粒子退化的缺陷,同时还存在峰值提取困难的问题;二是高斯混合法,基于线性高斯的假设条件,Vo提出了高斯混合概率假设密度(Gaussian Mixture PHD,GM-PHD)滤波算法[4]。该算法以高斯和的形式来近似多目标PHD,假设检测概率和存活概率与状态无关,且衍生目标有限集和新生目标有限集的PHD均具有高斯和形式,则通过对PHD的预测更新可得到PHD递推公式的解析解。高斯混合方法在峰值提取方面易实现,较粒子滤波方法在工程实现方面要简单很多,计算量相对较小,计算复杂度为O(nm),其中n为目标数目;m为观测数目。
3 基于PHD滤波的多目标跟踪性能评估指标
性能评估指标对滤波算法的选取、分析和评估起着很重要的作用,在进行单目标跟踪时,我们可以用最小均方误差法评估单目标跟踪的性能,但对于多目标来说,由于要考虑到目标数目问题,这就需要对多目标跟踪算法选择更适合的评估办法。目前,用于评价多目标跟踪算法的性能评估方法主要有3种:Hausdorff距离,Wasserstein距离和最优子模型分配(Optimal Sub-pattern Assignment,OS⁃PA)距离。
Hausdorff距离对多集合之间存在的势差不敏感,不能获得满意的性能评价,并且Hausdorff距离存在局限性,要求在两个集合具有相同势的时候,才可以采用处理。Wasserstein距离是Hoffman和Mahler基于最小平均意义下的均方根误差距离,提出的一种优于Hausdorff距离的评价方法,但该方法存在无法处理随机集其中一个为空集时的情况。OSPA距离是Vo研究团队提出的一种最新评价方法,它是一种用集合间差异程度来进行衡量的误差距离[5]。相对Wasserstein距离,OSPA距离有了很大的改进,避开了Wasserstein存在的不足。
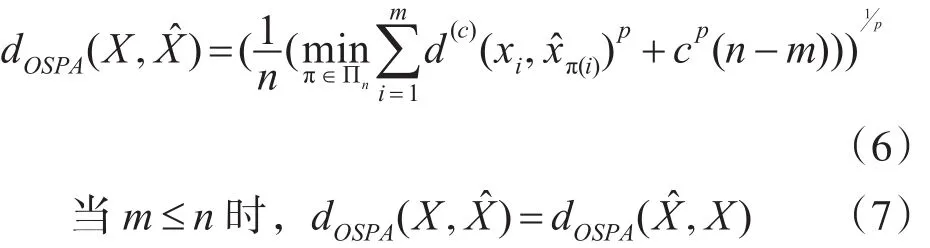
当m≥n时,
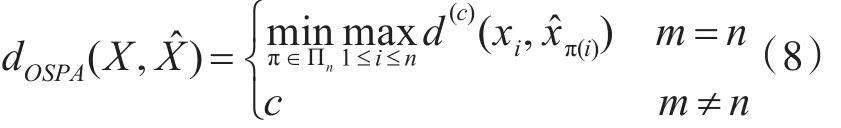
其中,d(c)(x,)=min(c,d(x,))表示x与之间的距离,c表示截取距离,p表示阶数,Πk表示排列组合的集合。
4 PHD滤波在多目标跟踪领域中的应用
近十几年,PHD滤波在以Mahler为代表的理论研究学者和以Vo为代表的工程技术人员的不断努力下,取得了大量研究成果。目前,PHD滤波技术已应用于很多领域的研究,如多机动目标跟踪、弱小目标检测前跟踪、扩展多目标跟踪、图像跟踪、群目标检测与跟踪、未知参数下的多目标跟踪和传感器管理等众多应用,接下来对在各应用领域的突出成果进行概述。
1)多机动目标跟踪:Vo将PHD滤波应用于多目标跟踪,提出一种多模型PHD滤波方法,采用粒子滤波方法进行近似求解,仿真表明该方法多目标跟踪明显优于单模型PHD滤波[6]。Pasha等同样将多模型方法引入到GM-PHD滤波方法中,同时考虑三种运动运动模型,在对机动目标跟踪中表现出比传统数据关联IMM-JPDA(Interacting Multiple Model JPDA)更好的性能[7]。
2)弱小目标检测前跟踪:Punithakumar等将PHD滤波引入到红外图像的多目标检测器跟踪中,利用粒子滤波方法实现对未知目标数的弱小多目标检测前跟踪[8],首次将PHD滤波思想应用于该领域研究,并通过粒子滤波实现方法验证了该方法的可行性。Tong等通过分析传统多目标跟踪问题中PHD滤波方法的适用模型与假设条件,建立了“标准”多目标观测模型,将噪声进行泊松化,解决了杂波数目服从泊松分布的问题,仿真表明,该方法在计算量和估计精度上都优于多目标粒子滤波[9]。
3)拓展多目标跟踪:Mahler在Gilholm等提出的量测空间模型基础上,将PGD滤波推广到拓展多目标跟踪,获得拓展目标PHD滤波器,推动了扩展多目标跟踪技术的发展,但该算法Mahler只是进行了理论推导,没有进行仿真实现[10]。2010年,在Vo提出的GM-PHD滤波器基础上,Granstrom等在线性高斯假设条件下给出了拓展多目标PHD滤波器的高斯混合实现形式,通过仿真验证了该滤波器的有效性[11]。王晓等在多模型方法启发下,提出了一种改进的MM-GM-PHD(MultipleModel GM-PHD)来处理机动扩展多目标跟踪的问题,取得了很好的效果[12]。
4)图像跟踪:Ikoma、Uchino和 Maeda将粒子PHD滤波器应用于时变光学图像特征点跟踪问题。Clark、Vo和Bell将GM-PHD滤波器应用于2维或3维的主动声纳图像跟踪问题,Wang等将粒子PHD滤波器应用于数字视频图像中的多目标跟踪问题[13]。
5)群目标检测与跟踪:瑞典国防研究局的研究团队在进行态势评估模拟器系统科研实践中,将PHD滤波器应用于PHD群目标跟踪通过一种基于多维分配方法的编队聚合算法对编队结构进行检测和分类,在每个编队结构上采用独立PHD滤波器进行群目标跟踪检测[14]。Clark等开展基于GM-PHD滤波方法的群目标跟踪问题研究,通过创建一个具有关联关系的目标估计状态图表来表示目标群,用来限制各目标高斯项在其对应的群中运动,并且通过PHD中航迹维持方法来识别目标群航迹[15]。
6)未知参数下的多目标跟踪:连峰等开展了未知杂波背景下的多目标跟踪研究,2009年,针对未知杂波环境问题提出一种利用有限混合模型(Fi⁃nite Mixture Models,FMM)和期望极大化算法对杂波模型进行估计的方法[16],2010年,提出一种对杂波分布满足静态条件的多目标跟踪方法[17]。周承兴针对未知测量噪声分布条件下提出一种基于风险评估的PHD滤波方法[18]。
7)传感器管理:Mahler提出了一种基于PHD滤波的多传感器多目标管理方法,该方法基于目标战术优先级进行相对排序,可以实现对重点目标的优先观测[19],EL-Fallah在研究中验证了该方法在简化仿真场景中,可以用粒子滤波方法实现。Mahler和EL-Fallah在研究PHD滤波器改进方法中,结合未知动态变化的杂波情形,提出了计算可行的后验期望目标数(Posterior Expected Number of Targets,PENT)公式,得到了一个统一未知动态杂波情形下的传感器管理方法[20]。
由于PHD滤波技术在解决多目标跟踪问题有着广泛的前景,在国外研究的推动下,国内越来越多的研究机构和人员开始从事该领域的研究探索,主要从事PHD滤波实现方式及PHD滤波器应用等方面研究。
5 PHD滤波技术展望
纵观上述内容,基于RFS理论的PHD滤波已经取得很多令人鼓舞的研究成果,着眼于PHD滤波的多目标跟踪研究,现将该领域研究存在的问题以及未来重点发展的几方面内容总结如下:
1)PHD滤波实现方法研究
目前PHD滤波的实现方法主要是序贯蒙特卡洛(粒子滤波)方法和高斯混合方法两种,但粒子滤波方法对密度函数的选择要求较高,同时该类函数难以确认,需要大量采样近似计算,计算能力要求较高,较难工程实现;高斯混合方法要进行线性高斯条件假设,目前虽然一些研究者采取近似方法可以处理非线性非高斯问题,但目标估计精度有所下降,有必要开展在计算复杂度和估计精度折中的算法研究。
2)多传感器多目标跟踪研究
目前基于PHD滤波的多传感器目标跟踪通常假设各传感器观测数据完全独立,采用序贯处理方式,计算复杂度小,但跟踪精度不高、稳定性较差。另一种是采用乘积多传感器PHD滤波方法,综合考虑多传感器观测信息,具有更好的跟踪精度和稳定性,但计算复杂度较高,难以实现。因此,如何实现精度更高、稳定更强同时易于工程实现的多传感器多目标跟踪是未来发展的方向。
3)多扩展目标跟踪方法研究
目前基于PHD滤波的多扩展目标跟踪方法大多是基于线性高斯模型的,具有一定的局限性,开展非线性非高斯的多扩展目标滤波方法研究更具有普适性,同时目前开展多扩展目标跟踪方法研究主要是二维模型,如果能够发展出扩展目标的三维扩展模型,则将能够更加准确和真实地描述目标,从而获得更多的扩展目标信息。
4)航迹生成方法研究
基于PHD滤波的多目标跟踪算法得到的是每一时刻目标数目和目标状态,相邻的目标状态之间没有航迹关联信息,并未给出连续时刻的目标间关系,未对所有目标的航迹进行估计。目前,基于PHD滤波的航迹生成方法主要是结合传统数据关联技术,将各离散时刻估计的多目标RFS视为“观测集合”,进而采用传统数据关联技术形成目标航迹,但该方法并没有考虑存在目标漏检和虚假估计的情况,将导致形成虚假航迹和一个目标会产生多条航迹,这将不利于监视场景的综合态势理解和分析。未来如何在PHD滤波框架下实现联合状态估计及航迹生成提取是值得研究的一个方向。
5)多目标联合检测、跟踪与分类方法研究
目前大多研究都将目标检测、跟踪与分类三个问题分开处理,然而这三个问题实际可以紧密耦合的,联合处理有望同时得到更优异的检测、跟踪与分类性能。现在关于目标联合跟踪与分类(Joint Target Tracking and Classification,JTC)和目标联合检测与跟踪(Joint Target Detection and Tracking,JDT)方面的研究有很多,但对目标联合检测、跟踪与分类(Joint Target Detection,Tracking and Classi⁃fication,JDTC)方法研究不多,主要原因是缺乏一种既有严格理论解释基础又存在有效实现途径的理论框架,但RFS理论的出现填补了这方面的空白,可以实现目标的检测、跟踪与分类同步处理,这将大大提高现代监视系统多目标信息的获取能力,具有更大的理论和现实意义。
6 结语
本文对基于PHD滤波的多目标跟踪发展和应用现状进行总结概述,对PHD滤波的基本原理和实现方法进行了介绍,并对未来该方法重点发展的几方面内容进行了展望,希望我们国内的科研人员未来在PHD滤波方面能取得更好的成就。
[1]杨峰,王永齐,梁彦等.基于概率假设密度滤波方法的多目标跟踪技术综述[J].自动化学报,2013,39(11):1944-1955.
[2]张洪建.基于有限集统计学的多目标跟踪算法研究[D].上海:上海交通大学,2009.31-32.
[3]李云湘.基于PHD滤波的多目标跟踪技术研究[D].长沙:国防科技大学,2012.33-35.
[4]Vo B-N.The Gaussian Probability Hypothesis Density Fil⁃ter[J].IEEE Transaction on Signal Processing,2006,54(11):4091-4104.
[5]张鹤冰.概率假设密度滤波算法及其在多目标跟踪中的应用[D].哈尔滨:哈尔滨工程大学,2012:28-29.
[6]Vo Ba-Tuong,Clark D-E,Vo Ba-Ngu.Bernoulli for⁃ward-backward smoothing for joint target detection and tracking[J].IEEE Trans on Signal Processing,2011,59(5):4473-4477.
[7]Pasha S-A,Vo B-N,Tuan H-D.A Gaussian mixture PHD filter for jump Markov system models[J].IEEE Transaction on Aerospace and Electronic Systems,2009,45(3):919-936.
[8]Punithakumar K,Kirubarajan T.A sequential Montel Car⁃lo probability hypothesis density algorithm for multitarget track-before-detect[C]//Proceedings of the 2005 SPIE,San Diego,California:SPIE,2005:587-594.
[9]Tong H-S,Zhang H,Meng H-D.Multitarget tracking be⁃fore detection via probability hypothesis density filter[C]//Proceedings of the 2010 International Conference on Elec⁃trical and Computer Engineering,Wuhan,China:IEEE,2010:1332-1335.
[10]Mahler R.PHD Filters for Nonstandard Targets,I:Ex⁃tended Targets[C]//The 12th International Conference on Information Fusion,Seattle,WA:IEEE,2009:915-921.
[11]Granstrom K,Lundquist C,Orguner U.Extended Target Tracking Using A Gaussian Mixture PHD Filter[J].IEEE Transactions on Aerospace and Electronic Sys⁃tems,2012,48(4):3268-3286.
[12]王晓,韩崇昭.用于机动目标跟踪的多模型概率假设密度滤波器[J].西安交通大学学报,2011,45(12):1-5.
[13]王晓.基于随机有限集的目标跟踪方法研究及最新进展[J].工程数学学报,2012,29(4):567-578.
[14]Ahlberg S,Horling P,Jored K.The IDF03 information fu⁃sion demonstrator[C]//Processing of the 7th Internation⁃al Conference on Information Fusion,Sunnyvale,CA:IEEE,2004:936-943.
[15]Clark D,Godsill S.Group target tracking with the Gauss⁃ian mixture probability hypothesis density filter[C]//Pro⁃ceedings of the 3rd International Conference on Intelli⁃gent Sensors,Sensor Networks and Information,Mel⁃bourne Qld:IEEE,2007:149-154.
[16]Lian F,Han C-Z,Liu W-F.Multitarget tarcking algo⁃rithm in unkown clutter[J].IEEE Transactions on Aero⁃space and Electronic Systems,2010,46(4):2066-2078.
[17]连峰,韩崇昭,刘伟峰.未知杂波环境下的多目标跟踪算法[J].自动化学报,2010,35(7):851-858.
[18]周承兴,刘喜贵.未知测量噪声分布下的多目标跟踪算法[J].航空学报,2010,31(11):2228-2237.
[19]R Mahler.Multitarget sensor management of dispersed mobile sensor[C]//Theory and Algorithms for Coopera⁃tiveSystems,Singapore:WorldScientic,2005:462-471.
[20]Mahler R,El-fallah A.Unified sensor management in un⁃kown dynamic clutter[C]//Proceedings of the 2010 Inter⁃national Society for Optics and Photonics,Orlando,FL:SPIE,2010:796-803.
