基于短时傅里叶变换的语音信号处理研究∗

赵晓雷

（渭南师范学院网络安全与信息化学院 渭南 714099）

1 引言

在人类生活中，信息交换的形式多种多样，而语音传递信息则成为交换信息的最有效、最常用的形式，由于在现实生活中获取语言时存在着各种各样的噪声，势必影响语音质量的高低。语音信号分析方法有多种，比如从时域方面进行分析，或者从频域这个方面进行分析，另外还有模型分析方法和非模型分析方法等等。傅立叶变换是将信号系统的时域和频域的特性联系起来的一种分析信号的方法，它不仅能够［1］用来分析信号中的成分，也可以将分析的成分再合成信号，同时，也可以利用其他形式的波比如方波等作为信号数据来使用。因此可以将傅里叶变换应用到语音信号处理上，在语音信号［2］处理上可以取得一定的效果。

2 语音信号分析

对语音信号分析是完成语音信号参数的特点分析，只有这样才有可能处理这些参数，比如语音通信、语音合成、语音识别等，而且，对音质而言，语音［3］由于采集过程中的限制和周围环境的影响也有好坏之分，比如识别率和影响率的大小，这些都会影响到分析出来语音信号的准确性和精确性。

语音分析无论是在选择使用的参数还是在分析方法上，都必须按帧［4］进行。“短时分析技术”它在整个语音信号的分析过程中都有贯穿，而且在整个过程中也是一个不平稳的过程。

2.1 语音信号的时域分析

时域分析顾名思义就是分析时域参数，语音信号的时域分析主要是通过对采集来的语音信号本身的时域参数进行分析［5］。进行语音分析时，时域波形是我们最能够直观看到的。从根本上讲语音信号的实质也就是一种时域，在进行语音信号分析时最常采用的方法就是时域分析法，也是应用与分析所采集信号的参数最基本的方法。

2.2 语音信号的频域分析

语音信号的频域分析是针对语音信号的频域特征进行分析。最常用的频域分析法有带通滤波器组法、傅里叶变换法、线性预测法［6］等。在用傅里叶变换表示语音信号之前，应先用短时傅里叶变换对语音信号的频谱进行分析，我们将所对应的频谱称为“短时谱”。

3 傅里叶变换

假设f(t)是t函数的一个周期，其中t需要满足一定条件，我们令其时间周期为两个时间单位，保持连续或者第一类间断点的各数为常数项，f(t)单调或可划分成有限单调区间，则F(t)以周期为2T的傅里叶级数收敛，和函数F(ω)也是一个以周期函数，周期为两个时间单位，并且在这些点上并不连续，这是一个有极限的函数，并且在一个固定周期里面，它的极值点个数也是常数有限，这就是达到狄里赫莱。

傅立叶变换公式：

3.1 FIR（Finite Impulse Response）滤波器

在音频信号的研究中，常常需要对信号进行滤波，去分析某一个频段的信号。我们经常使用的数字滤波器有两种，其中一种是FIR滤波器［7］，有限长单位冲激响应滤波器。它不但可以保证它的幅频特性，而且还具有严格的线性相位特性，而它的单位抽样响应的长度是有限的，所以滤波器是一种非常稳定的系统。另外一种是IIR滤波器，有延迟，不是线性相位的，同时其单位抽样响应是无限长的，所以两者相比，FIR有线性相位上的优势。但是实际运用中，FIR虽然是线性相位，但是也存在延迟，这样滤波后的信号总是有一定相位偏差，对信号分析造成很大干扰，即便是人为校正，也会带来很多工作量。实际应用中，我们需要的是一个零相移的滤波器［8］，这样在信号处理中，就能很好地保证我们非常关心的相位，而解决零相移问题，是可以实现的。在要求没有具体到滤波器的实时性的时候，我们将滤波器的相位频率特性设置为固定不变的0，从另外一个相对简单的思路来说，就是让一个信号序列在经过滤波器滤波后［9～10］，它的信号序列的相位没有发生任何变化，我们就将这种滤波器称之为零相移数字滤波器。

3.2 窗函数法设计FIR带通滤波器

窗函数法的设计思想：便是用窗函数法设计FIR滤波器在时域进行。窗函数法设计FIR滤波器的流程图如图1所示。

图1 窗函数法设计FIR滤波器的流程图

4 语音信号测试及分析

这里以一个语音信号为例子，采样时的频率为8000Hz。将在不同频带（对这段语音加入不同频段的噪声，加入噪声为高频余弦噪声振幅为0.3，频率为3000Hz，和高频率正弦噪声振幅为0.3，频率为10000 Hz，和低频正弦频率振幅为0.3，频率为10 Hz），使用汉明窗设计FIR和零相移FIR，分别滤波，滤波后计算两者的信噪比。通过对比它们滤波后的频谱和信噪比来判断滤波的好坏。

4.1 语音信号和混合噪声后的语言信号

语音信号进行采集的部分［11～12］，可以利用录音工具进行信号的采集，然后对音频格式进行转换音频格式，目的是为了使Matlab可以识别出来。

原始语音波形和频谱如图2，加入噪声后的语音波形和频谱图如图3所示。

4.2 FIR滤波器滤波后的信号

使用线性FIR滤波器对语音去噪得到波形图和频谱图，如图4。

使用线性相移FIR滤波后信噪比：-3.4388。

出现负数的原因是：FIR滤波后信号出现了相位延迟变化［13～14］，计算信噪比出现错位，得到负数，所以FIR滤波器对语音信号滤波会产生很大的相位缺信息丢失［15］，虽然频段上和幅值上基本符合要求，但是在加密水印等语音处理中，信号延迟，并且最后100个数据点丢掉了，意味着原始数据点信息的丢失。

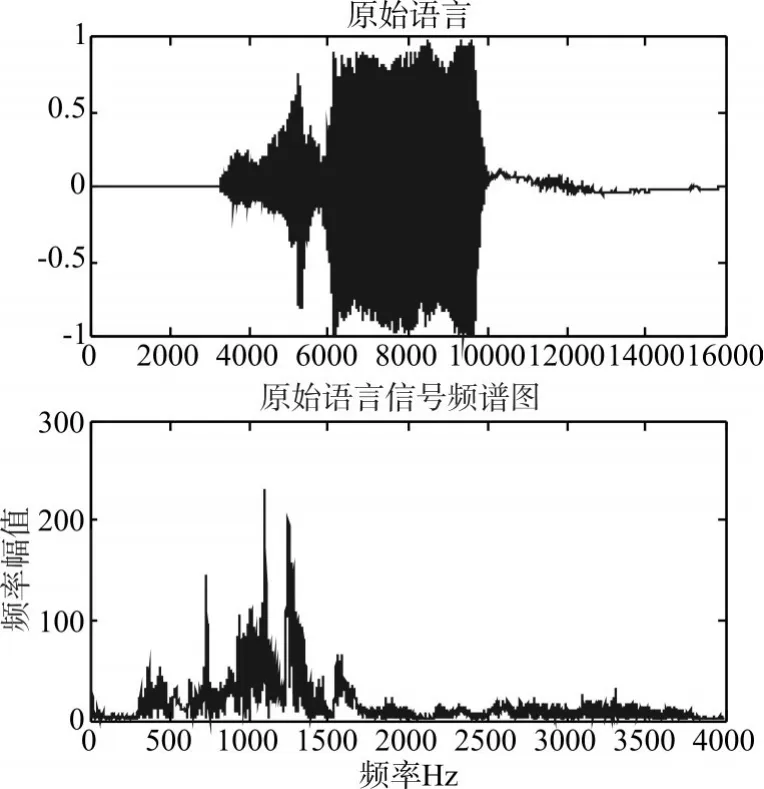
图2 原始语音波形和频谱出图

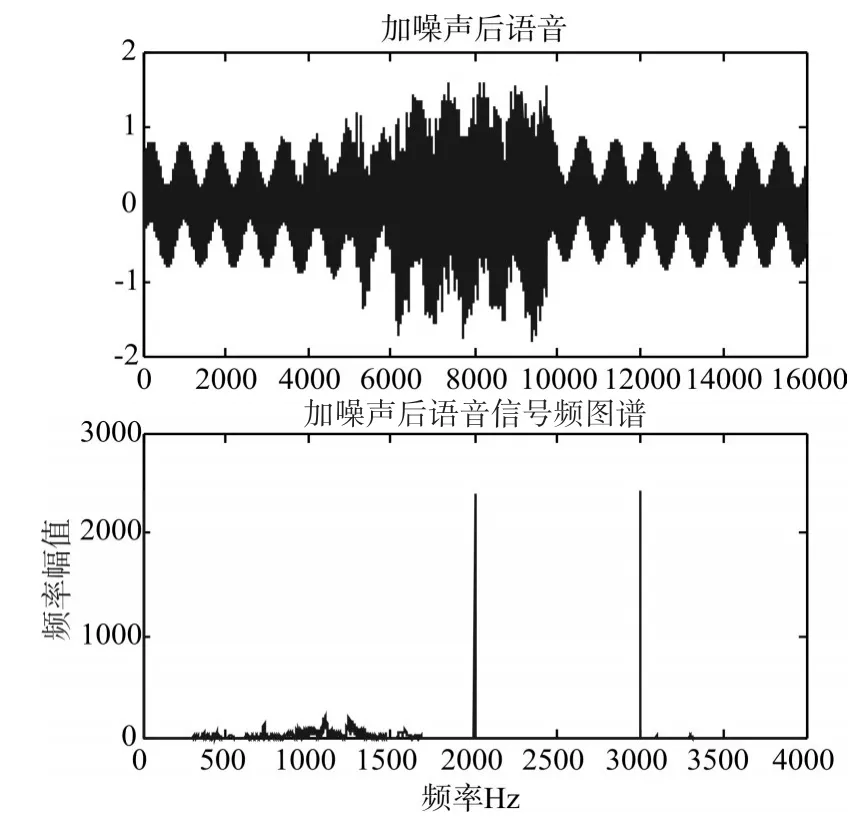
图3 加入噪声后语音波图和语音频谱图

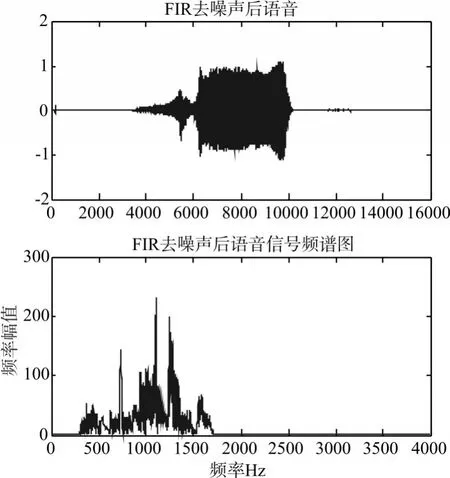
图4 去除噪音的波形图和频谱图

使用零相移FIR滤波器对信号滤波得到波形和频谱如图5，信噪比通过计算我们得到：加噪后信噪比：7.2679。

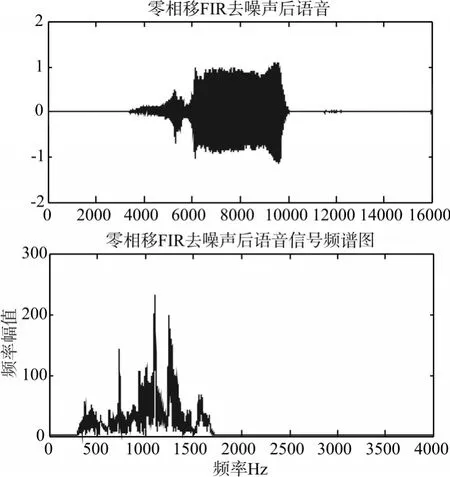
图5 零相移FIR滤波器对信号滤波波形图和频谱图

FIR去噪后信噪比：-3.4379。

零相移FIR去噪后信噪比：9.0203。

5 结语

在以上的实验中，相对普通滤波器使用零相移滤波器实现了信号的过滤，并且保留了很好的相位特性，零相移滤波器的过渡带衰减比较大。零相移滤波器的滤波结果既保持了滤波幅度和频域的特点，又很好地保留了相位信息，没有造成数据损失，所以零相移滤波器在语音滤波处理中拥有比线性FIR滤波器更多的优势。

［1］黄克武，陶然，吴葵，王越.分数阶傅里叶域与时域联合干扰抑制研究［J］. 中国科学：技术科学，2011（10）：1394-1404.

［2］Hong Kook Kim.Cepstrum-Domain Acoustic Feature Compensation Based on Decomposition of Speech and Noise for ASR in Noisy Environments［J］.IEEE Transac⁃tions on Speech and Audio Processing，2003，11（5）：435-446.

［3］Carrillo RE，Barner K E.Lorentzian based iterative hard thresholding for compressed sensing［C］//IEEE interna⁃tional Conference on Acoustics，Speech and Signal Pro⁃cessing.Prague，Czech Republic：IEEE Computer Soci⁃ety，2011：3664-3667.

［4］Carrillo RE，Barner K E.Lorentzian iterative hard thresh⁃olding：Robust compressed sensing with prior information［J］.IEEE Transactions on Signal Processing，2013：4822-4833.

［5］徐岩，孟静.基于粉红噪声的语音增强算法性能评价研究［J］.铁道学报，2011（04）：53-58.

［6］于永江，王菲.基于DSP的语音处理教学实验平台设计［J］. 电子测试，2016（17）100-101.

［7］刘少华.基于独立分量分析的语音信号分离及在数据采集卡上的实现［D］.南京：广西师范大学，2013.

［8］马春.基于压缩感知的语音信号重构方法研究［D］.合肥：安徽大学，2012.

［9］杨振，徐珑婷.语音信号处理中鲁棒性压缩感知关键技术［J］.数据采集与处理.2017（3）：232-245.

［10］孙林慧.语音压缩感知关键技术研究［D］.南京：南京邮电大学，2012.

［11］陆希玉，詹杰，唐昆，崔慧娟.低功耗通用语音处理平台的设计实现［J］.微型机与应用，2005（08）：16-19.

［12］周伟雄.语音信号的神经网络非线性分析模型及应用［D］.广州：华南理工大学，2010.

［13］Zhang Z，Rao B D.Recovery of block sparse signals using the framework of block sparse Bayesian learning［C］//IEEE international Conference on Acoustics，Speech and Signal Processing.Kyoto：IEEE，2012：3345-3348.

［14］刘鑫，金暄宏.基于LabVIEW的语音信号处理［J］.软件导报，2017（3）：135-137.

［15］SiggCD，Dikk T，Buhmann J M.Speech enhancement us⁃ing generative dictionary learing［J］.Audio，Speech，and Language Processing，IEEE Transactions on，2017，20（6）：1689-1712.