海洋集合预报中BGM型初始扰动生成及发展特征分析∗

刘敬一 过武宏 赵建昕

（海军潜艇学院 青岛 266100）

1 引言

目前模式的初值和模型本身存在误差，加上海洋本身是一个高度非线性的混沌系统，其中各个物理量具有强烈的时空易变性［1］，这导致单一的确定性预报结果的误差很大。针对确定性预报结果的不确定性问题，集合预报是一种有效的解决方法，它具体是通过一定的方法，获得具有某种概率密度分布特征的初值集合，分别对集合中的初值进行积分，得到预报结果的集合，据此分析预报系统概率密度分布随时间的发展演变情况。其中，每个初值均代表预报系统可能出现的真实情况。而初始扰动的生成作为集合预报中的一项重要技术，近年来得到广泛关注［2］。国内外学者针对不同的预报问题发展了不同的方法，目前主要有蒙特卡洛法（MC）［3］、增长模繁殖法（BGM）［4］、奇异向量法（SVs）［5～6］、变分同化法［7］、集合转换卡尔曼滤波法（ETKF）［8～10］以及条件非线性最优扰动法（CNOP）［11～12］等。

但是目前针对海洋集合预报初始扰动生成的研究还很不深入。本文主要利用区域海洋数值预报模式ROMS，基于BGM方法得到数值预报的初值集合，并就此分析初始扰动的发展特征，为研究扰动发展机理，进一步改善海洋数值预报初值质量，提高预报精度提供参考。

2 初始扰动方法介绍

BGM方法最初由美国国家环境预报中心（NECP）提出并投入业务化使用［13］，其具有明确的动力学意义，计算代价较低，预报效果较好。本文利用BGM产生初始扰动的主要步骤为［14］

1）在数值模式的初始分析场上加减同一个具有一定振幅大小的随机扰动，启动繁殖循环。该随机扰动由下式确定：

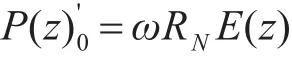
其中z代表模式的层数；是繁殖循环的初始扰动；ω是控制初始扰动的调整系数；E(z)是控制预报（没有初始扰动的预报）各层结果的均方根误差；RN是［-1，1］上的随机数，N为区域格点总数；

2）对加减扰动的初始场做固定时间间隔（如6h）的数值积分；

3）用加扰动预报结果减去减扰动预报结果，取其差值的1/2，得

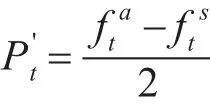
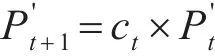
3ROMS模型配置与结果分析

3.1 模型配置

本文研究使用的区域海洋模式系统（Regional Ocean Modeling System，ROMS）是在近年的海洋科学研究中得到广泛应用的三维斜压环流模式，它采用了Boussinesq近似、流体静力近似和海水不可压缩近似，水平方向上采用正交曲线网格（Arakawa C），满足质量守恒，具有较高精度；垂直方向上采用非等比例分层的S坐标系，能够适当描述流场受地形的影响，对温跃层和底边界层等具有较高的解析度；

在本文研究中，ROMS的计算海区为东中国海（23.5°N～41.5°N，117°E～133°E），空间分辨率5km，计算网格点为372（经向）*506*（纬向）*32（垂向），其中在表层及底层做了适当的加密处理。模式的湍流封闭模型采用GLS垂向混合模型，侧边界采用辐射边界条件。模式所需的初始场及开边界条件数据取自HYCOM的模式结果；上表面的强迫场数据来源于NECP的CFSR再分析资料；地形数据使用的是NOAA提供的ETOPO2资料。

3.2 ROMS数值模拟结果分析

为消除不同资料之间的误差，获得稳定的初始场，以上述数据为初始、边界以及强迫条件，对研究海区积分3个模式年。此时，根据动能和势能随时间的变化曲线可以发现，模式结果已经基本稳定。再以ROMS稳定后的模式结果为初始条件，以HY⁃COM以及CFSR2006年1月的资料为边界及强迫场条件，对计算海区进行数值模拟。

3.2.1 温度场结果分析

图1表示，这种配置下模式的表层温度场预报结果（上）与同期AVHRR卫星遥感数据结果（下）比较，发现两者结果基本一致，验证了模式结果的可靠性。

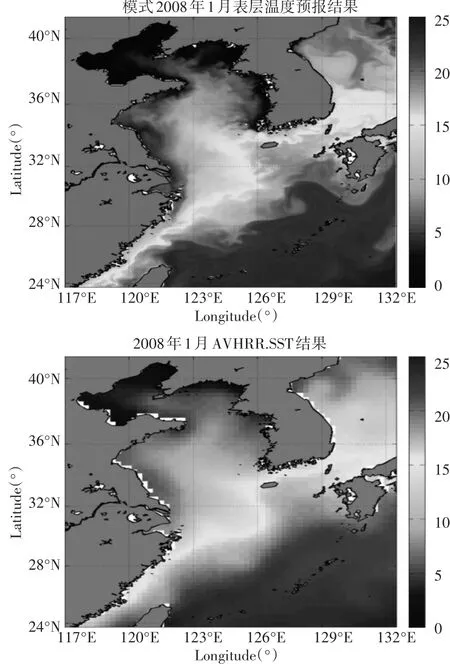
图1 数值模式预报结果与同期AVHRR卫星数据结果

3.2.2 流场结果分析

图2表示，这种配置下模式的表层流场预报结果（上）与同期卫星遥感资料结果（下）比较，发现模式基本预报出了区域内主要流场（如黑潮流系）以及其附近一些涡旋的特征，进一步验证了模式结果的可靠性。这里的卫星遥感资料指同期NOAA的OSCAR数据资料。

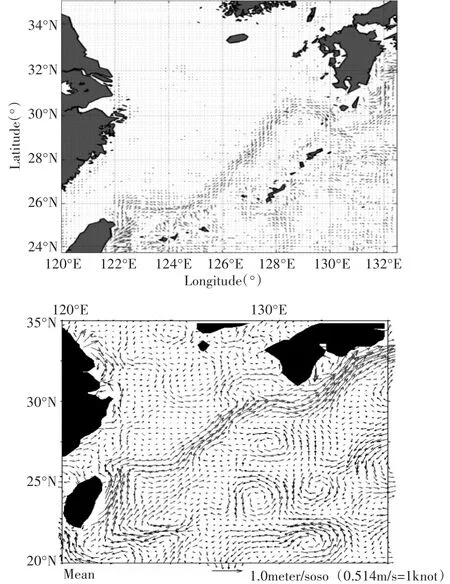
图2 数值模式预报结果与同期OSCAR卫星数据结果

4 扰动发展特征分析

4.1 试验方案

BGM集合预报试验方案的扰动初始模大小取模式24h温度场预报的均方根误差，空间上服从［-1，1］上的随机分布，将该初始模作为扰动叠加到分析场上进行繁殖，繁殖周期6h，经3天繁殖培养得BGM型的初始扰动，并作为一个集合预报初始扰动的成员，重复以上工作，得到一组成员数为16的初始扰动集合。最终将这16个成员的预报结果的等权平均作为BGM集合预报的预报结果。

4.2 扰动发展特征分析

试验结果表明，未经BGM培养的初始扰动在空间中无规则分布，这种扰动结构没有明确的物理意义；经BGM循环培养后（图3），初始扰动分布发生明显的变化，初始扰动在强斜压海区（如黑潮流域）及开边界处发展较快，而其他区域的初始扰动随繁殖过程被系统耗散，结果反映出初始扰动的发展受背景流场的影响，具有一定的动力学意义。

为进一步分析BGM型初始扰动的发展特征，选取台湾东北部初始扰动发展强弱不同的两块海区，其中扰动发展强区（25°N～27°N，121.5°E～123.5°E）、扰动发展弱区（29°N～31°N，123°E～125°E），检验初始扰动对预报结果影响的目标区位置为（27°N～29°N，125°E～127°E）。在模式稳定运行的基础上，以2006年1月1日HYCOM结果为基准初值，其他模式环境设置均相同，设计以下试验，观察各自对目标区（区域R3）未来14天温度场的预报误差发展：

1）初值中，没有初始扰动；

2）初值中，在初始扰动发展强的区域（区域R1）叠加随机扰动；

3）初值中，在初始扰动发展强的区域（区域R1）叠加BGM型扰动；

4）初值中，在初始扰动发展弱的区域（区域R2）叠加随机扰动。

需要特别说明的是，以上三种试验的随机扰动来源于同一个扰动种子，即随机扰动的模型及空间分布均一致，以此保证试验变量的唯一性。

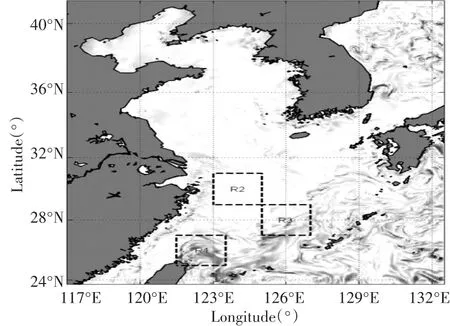
图3 BGM培养后的表层温度场初始扰动结构

分别将2、3、4试验结果与试验1结果比较得到预报误差，从预报检验区（区域R3）内表层温度场预报均方根误差结果来看：随预报时刻的增加，扰动发展强区（区域R1）初始扰动引起的预报均方根误差增长较快，其中具有BGM形态的初始扰动在预报检验时刻（第14天）的均方根误差是无空间形态的随机扰动误差的近三倍；而扰动发展弱区（区域R2）的初始扰动对预报检验区的温度场预报精度影响甚小，预报时刻的均方根误差仅为0.05°C。

由图4可见不同位置、不同形态上的初始扰动，对预报结果的影响差异很大，若提高在扰动发展强区中的初值质量，将有效改善预报效果。

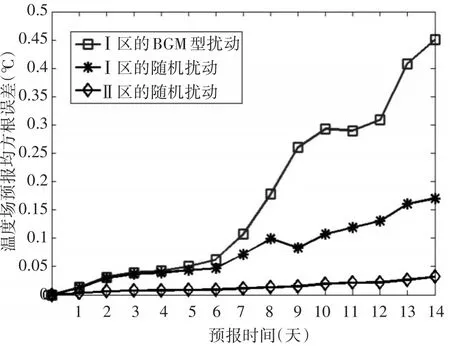
图4 预报检验区R3内表层温度场预报均方根误差

5 结语

本文基于BGM方法，结合ROMS海洋数值预报模式，研究了集合预报初始扰动的生成方法，给出了经BGM繁殖培养的初始扰动场，其表现出明显的时空特征，具有一定动力学意义。在此基础上，分别选取扰动发展强、弱两个区域做叠加不同形态初始扰动的对比试验，通过观测检验区内温度场预报的均方根误差大小发展情况，初步分析了初始扰动的发展特征，具有BGM型空间特征的初始扰动发展最强，在预报时刻对结果的影响远大于随机初始扰动的影响。

［1］王辉.海洋可预报性和集合预报研究综述［J］.地球科展，2014，29（11）：1212-1225.

［2］陈静，陈德辉，颜宏.集合数值预报发展与研究进展［J］.应用气象学报，2002，13（4），497-507.

［3］Leith C S.Theoretical skill of Monte Carlo forecasts［J］.Mon.Wea.Rev，1974，102：409-418.

［4］Toth Z，Kalney E.Ensemble forecasting at NMC：The gen⁃eration of perturbations［J］.Bull.Amer.Meteor.Soc. ，1993，74：2317-2330.

［5］Molteni F，Buizza R，et al.The ECMWF ensemble predic⁃tion system：methodology and validation［J］.Quart.J.Roy.Meteor.Soc.，1996，122：73-119.

［6］郑峰.集合预报初值扰动在天气预报中的应用研究进展［J］.科技导报，2008（26）：90-95.

［7］龚建东，李维京，丑纪范.集合预报最优初值形成的四维 变 分 同 化 方 法［J］.科 学 通 报 ，1999，44（10）：1113-1116.

［8］赵晓琳，朱国富，李泽椿.基于TIGGE资料识别适应性观测敏感区的应用研究［J］.应用气象学报，2010，21（4）：405-415.

［9］Petersen G N，S J Majumdar and A J Thorpe，The proper⁃ties of sensitivearea predictions based on the ensemble transform Kalmna filter（ETKF）［J］.Q.J.R.Meteor.Soc，2017（133）：697-710.

［10］马旭林，薛纪善，陆维松.GRAPES全球集合预报的集合卡尔曼变换初始扰动方案初步研究［J］.气象学报，2008，66（4）：526-536.

［11］穆穆，姜智娜.集合预报初始扰动产生的一个新方法：条件非线性最优扰动［J］.科学通报，2007，52（12）：1457-1462.

［12］姜智娜，穆穆，王东海.基于条件非线性最优扰动方法的集合预报试验［J］.中国科学D辑：地球科学，2008，38（11）：1444-1451.

［13］Toth Z，Kalney E.Ensemble forecasting at NECP and the breed method［J］.Monthly Weather Review，1997（125）：3297-3319.

［14］关吉平，张立凤，马环宇.基于增长模繁殖法的初始分析误差计算及集合预报试验［J］.气象科学，2009，29（3）：317-322.