基于稀疏样本选优的机载雷达动目标检测算法
2018-04-26龚清勇王成燕
龚清勇, 王成燕
(南京邮电大学通信与信息工程学院,江苏 南京 210003)
0 引 言
空时自适应处理(space-time adaptive processing,STAP)是机载雷达在强杂波环境中进行动目标检测的有效技术[1-4]。STAP的性能依赖于杂波协方差矩阵的构建精度。依据RMB准则[1],当用来估计杂波协方差矩阵的训练样本充足、满足独立同分布(independent and identically distributed,IID)时才不会影响动目标的检测性能。然而,机载雷达实际工作在非均匀环境中,上述条件很难满足。当训练样本中存在干扰目标时会引起信号相消,造成漏警,降低对动目标的检测性能。针对此问题,学者们提出利用非均匀检测器(nonhomogeneous detector,NHD)[5]来检测训练样本中是否含有干扰目标,对含有干扰目标的训练样本加以剔除。比较典型的NHD有:广义内积(generalized inner project,GIP)及其改进的算法、自适应功率剩余(adaptive power residual,APR)及其改进的算法等。
随着稀疏恢复和压缩感知技术的发展,基于稀疏空时谱恢复的STAP算法(STAP algorithm based on sparse recovery,SR-STAP)[6-9]成为近几年研究的热点。由于杂波谱在角度-多普勒频域具有稀疏性,利用稀疏恢复技术来估计高分辨率的空时二维杂波谱。比较典型的SR-STAP有:联合稀疏功率谱恢复的STAP算法[10]及其改进的算法[11]、直接数据域SR-STAP及其改进的算法[6]等。这些算法能够利用稀疏恢复技术对训练样本数据以及待检测距离单元的数据进行重构。为了提高对待检测单元杂波协方差矩阵的估计精度,文献[12]提出一种训练样本选优SR-STAP算法,选择与待检测距离单元的数据较相似的训练样本参与杂波协方差矩阵估计,从而利用较少的训练样本得到精度较高的杂波协方差矩阵,但该算法只适合均匀样本,当训练样本中存在干扰目标时会造成信号相消,影响动目标的检测性能。为了克服训练样本中的干扰目标,文献[10]提出基于联合稀疏功率谱恢复的STAP算法(STAP algorithm based on joint sparse recovery,JSR-STAP),利用训练样本中杂波与干扰目标稀疏恢复系数的不相关性,去除训练样本中的干扰目标,从而达到抑制干扰目标的目的,但是该算法在构建杂波协方差矩阵时没有加入待检测距离单元的数据也没有对训练样本进行选优,使得构建的杂波协方差矩阵精度下降,进而影响动目标的检测性能。
为了提高动目标的检测性能,本文提出一种基于稀疏样本选优的机载雷达动目标检测算法,该算法先对训练样本进行选优,再利用l2范数选择合适的稀疏恢复幅值,去除选优后训练样本和待检测距离单元中与杂波不相关的数据[10]。仿真验证了本文算法能够提高动目标的检测性能。
1 信号模型


图1 正侧视阵机载雷达几何模型Fig.1 Side looking array airborne radar geometric
由几何模型可知,第l个距离单元接收到的杂波加噪声信号[4]为
(1)
式中
Si(fdi,fsi)=Ssi(fsi)⊗Sti(fdi)
(2)
Ssi(fsi)=[1,exp(j2πfsi),…,exp(j2π(N-1)fsi)]T
(3)
(4)
(5)
(6)
式中,Nc为第l个距离环中杂波散射源的数量;σi为第l个距离环中第i个杂波散射源的幅度;nl为第l个距离环的噪声;Si(fdi,fsi)为第l个距离环中第i个杂波散射源的空时导向矢量;Ssi(fsi)为第l个距离环中第i个杂波散射源的空域导向矢量;Sti(fdi)为第l个距离环中第i个杂波散射源的时域导向矢量;⊗为Kronecker积;fdi/fr为第i个杂波散射源的归一化多普勒频率;fsi为第i个杂波散射源的空间频率。
2 基于稀疏的STAP算法
2.1 稀疏性分析

(7)
因此,杂波主要分布在由式(7)决定的杂波脊线上[13-15]。
将杂波所在的角度-多普勒频域进行离散化,空间角度域离散化程度为ρs(ρs≫1),多普勒域离散化程度为ρd(ρd≫1),即空间角度域划分为Ns=ρsN个离散点,多普勒域划分为Kd=ρdK个离散点,则第l个距离单元接收到的杂波加噪声信号可表示为
(8)
式中,σl为NsKd×1维(NsKd≫NK)第l个距离单元空时平面内的幅度。由上面分析知杂波主要分布在式(7)决定的杂波脊线上,因此σl是个稀疏向量。稀疏向量中非零的值对应显著分量(稀疏向量中除显著分量外,其他分量很小可以记为0),显著分量的个数等于稀疏度。稀疏度的选取方法[6]如下:
获得离散化后杂波脊线沿空间角度轴占据的格子数为

(9)

获得离散化后杂波脊线沿多普勒轴占据的格子数:

(10)
理论上,稀疏度的取值范围为

(11)
当ρs≫1,ρd≫1时,可以采用式(12)来估计稀疏度。


(12)
Φ是NK×NsKd维由空时导向矢量构成的冗余基矩阵,假设ΦnsKd+kd+1为Φ中第nsKd+kd+1列,则满足[16]
ΦnsKd+kd+1=

(13)
式中,ns=0,1,…,Ns-1;kd=0,1,…,Kd-1;Δωs为离散化后空时平面最小空域角频率间隔;Δωt为离散化后空时平面最小时域角频率间隔。
2.2 稀疏恢复
由第2.1节分析可知,σl具有稀疏性,可以依据稀疏恢复理论[17-20]求得
s.t.‖xl-Φσl‖2≤ε
(14)
式中,‖·‖p为lp范数;ε为稀疏恢复的误差容限(取值与噪声功率有关)[6,16]。
由于l0范数最小化优化问题计算量巨大,研究已证明,当σl足够稀疏时可以用l1范数代替l0范数[21],则式(14)可以表示为
s.t. ‖xl-Φσl‖2≤ε
(15)

2.3 基于稀疏杂波协方差矩阵的构建
由文献[12]可知,第l个距离环的杂波协方差矩阵可以表示为
(16)
式中
(17)
为了精确地估计杂波协方差矩阵,通常选择多个距离单元的训练样本,估计的杂波协方差矩阵可表示为
(18)
式中,L为参与构建杂波协方差矩阵的样本总数。
3 基于稀疏样本选优动目标检测
本文根据JSR-STAP算法和基于训练样本选优的SR-STAP算法,提出一种基于稀疏样本选优的机载雷达动目标检测算法。本文提出的算法与JSR-STAP算法相比,一方面能够对重构的训练样本进行选优,另一方面在构建杂波协方差矩阵时加入待检测距离单元的数据(准备两份待检测距离单元的数据,一份采用JSR-STAP算法去除待检测距离单元中的目标信号,用来参与杂波协方差矩阵的构建;另一份不做处理用来进行动目标的检测),提高了构建杂波协方差矩阵的精度,从而提高机载雷达动目标的检测性能;与基于训练样本选优的SR-STAP算法相比,能够利用l2范数选择合适的稀疏恢复幅值,去除选优后训练样本和待检测距离单元中与杂波不相关的数据,消除干扰目标对动目标检测性能的影响,从而提高机载雷达的动目标检测性能。算法实现步骤如下:

步骤2分别计算L-1个训练样本与待检测距离单元样本中显著分量具有相同位置的幅值的数量,标记为Nl,其中l=1,2,…,L-1。
步骤3对Nl按照降序进行排列。
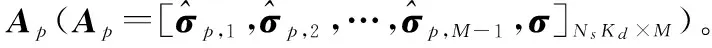
步骤5为了使M-1个训练样本和待检测距离单元之间的稀疏约束相互增强,对矩阵Ap按行求l2范数,即
(19)
将式(19)所得的列向量按元素值由大到小的顺序记录元素的位置,并构成位置集合Γ。
(20)
式中
(21)
(22)
(23)
步骤7如果满足Δm(i)<ε或者i=NsKd,进入步骤8,否则令i=i+1,返回到步骤6。
步骤8构建第m个距离单元的杂波协方差矩阵为
(24)
由式(24)可得M个距离单元联合处理后的杂波协方差矩阵可表示为
(25)
使用式(25)构建的杂波协方差矩阵进行STAP处理,可以达到稳健的动目标检测性能。
4 仿真实验
仿真场景为具有均匀线性阵列的正侧视机载相控阵雷达系统。阵元数N=10,脉冲数K=10,雷达工作波长λ=0.25 m,载机飞行的速度v=150 m/s,载机飞行的高度H=6×103m,阵元间距d=0.5λ,脉冲重复频率fr=2v/d,采样距离环间距ΔR=49 m,待检测距离单元(第81个距离单元)两侧分别取80个距离单元作为训练样本(即L-1=160),杂噪比为50 dB,选优后样本数M=71。第40、60、125、165个距离单元分别在方位角30°,fd/fr=0.125处加一个干扰目标,其信杂噪比(signal-to-clutter-noise ratio,SCNR)分别为-25 dB 、-10 dB 、0 dB 、-15 dB。图2给出了改善因子对比图,图3为距离单元输出功率,图4和图5为利用基于图像特征空时处理的地面动目标检测(image feature-based space-time processing,IFSTP)算法[27-28]进行的目标信号提取对比图。图中仿真都是100次独立实验的平均值。
在待检测距离单元加入一个位于方位角30°,fd/fr=0.125的运动目标。改善因子对比如图2所示。

图2 改善因子对比Fig.2 Improvement factor comparison
从图2可以看出,本文算法在主杂波处杂波凹口最窄,较其他两种算法本文算法不易造成漏警;本文算法在干扰目标所在的fd/fr=0.125处没有形成凹陷,不易造成虚警;本文算法相比训练样本选优SR-STAP算法平均改善8.25 dB,相比JSR-STAP算法平均改善1.55 dB。
在待检测距离单元分别加入一个SCNR为-10 dB和-25 dB,方位角为30°,fd/fr=0.125的运动目标。图3是第81~120个距离单元(第81个距离单元为待检测距离单元)的滤波输出功率。
为了验证所提出方案的可行性,制作了一台实验样机,输入电压为0~120 V;输出电压为380 V,额定功率1 000 W。
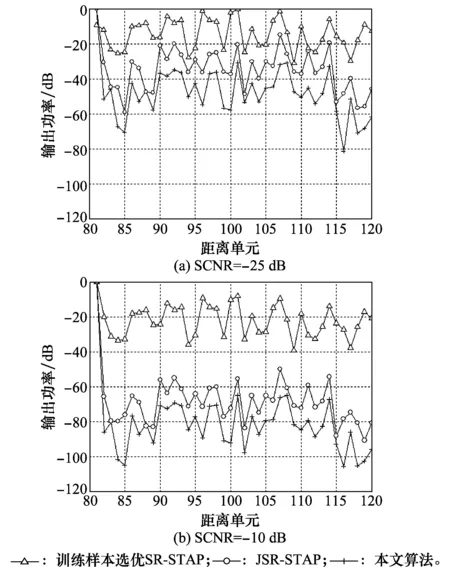
图3 距离单元输出功率Fig.3 Range cell output power
从图3(a)可以看出,SCNR=-25 dB时,本文算法效果最好。本文算法待检测距离单元的输出功率与其他距离单元中最大的输出功率差为30.7 dB,训练样本选优SR-STAP算法待检测距离单元的输出功率与其他距离单元中最大的输出功率差为-9.1 dB,JSR-STAP待检测距离单元的输出功率与其他距离单元中最大的输出功率差为14.7 dB。
从图3(b)可以看出,SCNR=-10 dB时,本文算法效果最好。本文算法待检测距离单元的输出功率与其他距离单元中最大的输出功率差为64.9 dB,训练样本选优SR-STAP算法待检测距离单元的输出功率与其他距离单元中最大的输出功率差为8.0 dB,JSR-STAP待检测距离单元的输出功率与其他距离单元中最大的输出功率差为49.7 dB。
在待检测距离单元加入一个位于方位角40°,fd/fr=0.15的运动目标。利用IFSTP算法,通过设定相同的增长距离,提取目标信息。图4是训练样本选优SR-STAP算法和本文算法的目标信号提取结果。
从图4(a)可以看出,当训练样本中存在干扰目标时,训练样本选优SR-STAP算法由于未对干扰目标进行剔除,在稀疏恢复空时谱时会包含干扰目标的信息从而影响动目标检测性能。因此在提取出位于方位角40°,fd/fr=0.15处的运动目标的同时,在方位角30°,fd/fr=0.125处也提取出目标(干扰目标)的信息,造成虚警;从图4(b)可以看出,本文算法能够正确提取出目标信息且没有造成虚警。

图4 目标信号提取ⅠFig.4 Target signal extraction Ⅰ
在待检测距离单元加入两个运动目标位于方位角40°,fd/fr=0.15和方位角55°,fd/fr=0.20处。图5是JSR-STAP算法和本文算法的目标信号提取结果。

图5 目标信号提取ⅡFig.5 Target signal extraction Ⅱ
从图5可以看出,JSR-STAP算法只是剔除了干扰目标未对训练样本进行选优,造成稀疏恢复的杂波空时谱较本文算法稀疏恢复的杂波空时谱宽,从而影响动目标的检测性能。由于JSR-STAP算法杂波空时谱较宽,图5(a)只提取出位于方位角40°,fd/fr=0.15处的目标,未提取出位于方位角55°,fd/fr=0.20处的目标,造成漏警。由图5(b)可以看出,本文算法能够正确提取出目标信息且没有造成漏警。仿真结果进一步证明了本文算法的有效性。
5 结 论
本文针对存在干扰目标的非均匀样本中动目标检测性能下降的问题提出一种基于稀疏训练样本选优的机载雷达动目标检测算法,利用杂波谱的稀疏恢复算法对接收到的数据进行重构,对训练样本进行选优,去除选优后训练样本中的干扰目标,从而提高机载雷达动目标检测性能。仿真结果表明,本文算法动目标检测的性能优于训练样本选优SR-STAP算法和JSR-STAP算法。
参考文献:
[1] WANG Y L,LIU W J,XIE W C. Research progress of space-time adaptive detection for airborne radars[J]. Journal of Radars,2014, 3(2):201-207.
[2] YANG Z, QUAN G, MA Y, et al. Compressive space-time adaptive processing airborne radar with random pulse repetition interval and random arrays[C]∥Proc.of the 4th IEEE International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar and Remote Sensing, 2016:247-251.
[3] ZHU Z, KAY S, COGUN F,et al. On detection of nonstationarity in radar signal processing[C]∥Proc.of the IEEE Radar Conference, 2016:1-4.
[4] WANG X R, ABOUTANIOS E, AMIN M G. Slow radar target detection in heterogeneous clutter using thinned space-time adaptive processing[J]. IET Radar, Sonar & Navigation, 2016, 10(4):726-734.
[5] 龚清勇. 非均匀环境下机载雷达STAP技术研究[D]. 南京:南京航空航天大学,2010.
GONG Q Y. Study on STAP methods for airborne radar in nonhomogeneous enviro nment[D].Nanjing: Nanjing University of Aeronautics and Astronautics,2010.
[6] 孙珂. 非均匀杂波环境下基于稀疏恢复的STAP技术研究[D]. 北京:清华大学,2011.
SUN K. STAP technique using sparse recovery in heterogeneous clutter scenario[D]. Beijing: Tsinghua University, 2011.
[7] MA Z, LIU Y, WANG X. Sparsity based space-time adaptive processing using message passing[C]∥Proc.of the 3rd IEEE International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar and Remote Sensing, 2015:258-262.
[8] SEN S. Sparsity-based space-time adaptive processing using OFDM radar[C]∥Proc.of the IEEE International Waveform Diversity & Design Conference, 2012:160-165.
[9] YANG Z, LI X, WANG H, et al. Sparsity-based space-time adaptive processing using complex-valued Homotopy technique for airborne radar[J]. IET Signal Processing, 2014, 8(5):552-564.
[10] 高志奇,陶海红,赵继超.基于联合稀疏功率谱恢复的机载雷达稳健STAP算法研究[J].电子学报,2016,44(11):2796-2801.
GAO Z Q, TAO H H, ZHAO J C. Robust STAP algorithm based on joint sparse recovery of clutter spectrum for airborne radar[J]. Acta Electronica Sinina, 2016,44(11):2796-2801.
[11] MA Z Q, LIU Y M, MENG H D, et al. Jointly sparse recovery of multiple snapshots in STAP[C]∥Proc.of the IEEE Radar Conference, 2013:1-4.
[12] HAN S D, FAN C Y, HUANG X T. A novel training sample selection method for STAP based on clutter sparse recovery[C]∥Proc.of the IEEE Progress in Electromagnetic Research Symposium, 2016:2275-2279.
[13] YANG Z C, LI X, WANG H Q,et al. On clutter sparsity analysis in space-time adaptive processing airborne radar[J]. IEEE Geoscience and Remote Sensing Letters,2013,10(5):1214-1218.
[14] YANG Z, LI X, WANG H, et al. Knowledge-aided STAP with sparse-recovery by exploiting spatiotemporal sparsity[J]. IET Signal Processing, 2016, 10(2):150-161.
[15] ZHU Y, YANG Z C, HUANG J J. Robust sparsity-based space-time adaptive processing considering array gain/phase errors[C]∥Proc.of the 13th IEEE International Conference on Signal Processing, 2016:1624-1628.
[16] 王伟伟,廖桂生,朱圣棋,等. 一种基于压缩感知的地面运动目标检测方法[J]. 电子与信息学报, 2012,34(8): 1872-1878.
WANG W W, LIAO G S, ZHU S Q, et al. A ground moving target indication method based on compressive sensing[J]. Journal of Electronics & Information Technology,2012,34(8):1872-1878.
[17] DONOHO D L, ELAD M, TEMLYAKOV V N. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Trans.on Information Theory, 2006, 52(1):6-18.
[18] SEN S. Low-rank matrix decomposition and spatio-temporal sparse recovery for stap radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8):1510-1523.
[19] QUAN G, YANG Z, HUANG J, et al. Sparsity-based space-time adaptive processing in random pulse repetition frequency and random arrays rada[C]∥Proc.of the IEEE 13th Interna-tional Conference on Signal Processing, 2016:1642-1646.
[20] ZHU Y, YANG Z, HUANG J. Sparsity-based space-time adaptive processing considering array gain/phase error[C]∥Proc.of the CIE International Conference on Radar, 2016:1-4.
[21] DONOHO D L, ELADAR M. Optimally sparse representation in general (nonort-hogonal) dictionaries via L1 minimization[J]. IEEE Trans.on Signal Processing, 2003,12 (6):197-220.
[22] HONG L W, SHU W. Adaptive sparsity matching pursuit algorithm for sparse reconstruction[J]. IEEE Signal Processing Letter, 2012, 19(8):471-474.
[23] HUANG W Q, ZHAO J L, LV Z Q, et al. Sparsity and step-size adaptive regularized matching pursuit algorithm for compressed sensing[C]∥Proc.of 7th IEEE Joint Internatinal Information Technology and Artificial Intelligence Conference, 2014:536-540.
[24] LONG X, HU X, SHAODONG L, et al. A fast multiple orthogonal matching pursuit algorithm for jointly sparse recovery[C]∥Proc.of the CIE International Conference on Radar, 2016:1-3.
[25] ZHANG X, ZHOU B. Fast iterative reweighted least squares algorithm for sparse signals recovery[C]∥Proc.of the IEEE International Conference on Digital Signal Processing, 2016:208-212.
[26] YANG X, SUN Y, ZENG T, et al. Iterative roubust sparse recoery method based on focuss for space-time adaptive processing[C]∥Proc.of the IET International Radar Conference, 2015:1-6.
[27] HAI D, BRAHAM H, MICHAEL C W. Image feature-based space-time processing for ground moving target detection[J]. IEEE Signal Processing Letter, 2006, 13(4): 216-219.
[28] GENG Z, DENG H. Performance evaluation of image feature-based space-time processing (IFSTP) for moving target detection[C]∥Proc.of the IEEE Antennas and Propagation Society International Symposium, 2013:1024-1025.
