竞争失效下多元退化建模的导弹贮存寿命评估
2018-04-26蔡忠义项华春王泽洲
蔡忠义, 项华春, 王 攀, 王泽洲, 李 超
(空军工程大学装备管理与安全工程学院, 陕西 西安 710051)
0 引 言
贮存寿命是导弹的一项重要战技指标,关系到导弹的战备完好性和快速反应能力。通常情况下,导弹在贮存期内发生的失效是弹上多部件退化失效和突发失效之间竞争的结果[1]。长期修理经验表明,贮存期内弹上关键部件的失效占导弹失效的比例很高。通过对弹上部件的性能参数进行定期测试、分析与评估,可以评估导弹的健康状态[2-3]。关于竞争失效下多元退化建模研究可分为两部分。
一是多元退化建模,即对多个性能参数的产品进行退化建模[4-5],常见的处理方法有两种。①将产品多个性能参数融合为一个可以描述产品一个整体退化状态的性能参数,一般可采用贝叶斯线性模型[6]、状态空间模型[7-8]、支持向量机[9-10]等,建立产品的整体退化状态与多个性能参数之间的关系模型。文献[6]采用贝叶斯线性模型,建立了多个测试参数与其累计退化量之间的线性关系,但对于多个参数与退化量之间的非线性关系就难以适用。②直接建立多个性能参数的联合寿命分布模型[11-12]。一般采用Copula函数[13-14]、多元正态分布[15]等,描述多个性能参数之间的相关性,Copula函数一般只适用于二元相关性退化建模。文献[15]采用多元正态分布来描述多个性能参数之间的相关性,但使用前提是各性能参数的边际分布为正态分布且存在线性相关性。
二是退化失效与突发失效之间的竞争失效建模[16]。按照这两种失效模式之间是否独立,可分为两种情况。一种是两种失效模式之间独立的研究[14,17],将产品的可靠性模型看作是简单的串联模型,会降低导弹贮存可靠性评估的准确性;另一种是产品的突发失效受其性能退化影响的研究,一般采用比例危险模型[18-19]、位置-尺度模型[20]、退化阈值-冲击(degradation threshold-shock,DTS)模型[21]等,描述性能退化对突发失效率的定量影响关系,进而建立退化失效与突发失效之间的相关性竞争模型。文献[21]采用DTS模型,建立了突发失效与性能退化、环境因素之间的定量关系模型,评估精度高,但建模过程较复杂。
因此,本文首先分析导弹失效模式,建立导弹竞争失效模型;然后引入状态空间模型,将弹上多个关键部件特征电压转化为一个整弹退化程度;最后采用多个随机过程模型,建立整弹退化程度数据的退化模型;采用比例危险模型,建立考虑性能退化影响的突发失效模型。
1 竞争失效建模
1.1 基本假设
(1) 导弹失效是多个关键部件退化失效与突发失效之间竞争的结果,多个关键部件退化数据可通过状态空间模型转化为整弹退化程度数据。
(2) 导弹在贮存期内定期进行测试时,激励信号无输出或超出规定范围,则判断为突发失效,此次测试时间记为突发失效时间。
(3) 导弹突发失效时间服从Weibull分布,突发失效率与当前时刻的退化程度有关。
1.2 竞争失效模型
导弹贮存期内失效是弹上多部件退化失效与突发失效相互竞争的结果。通过分析导弹返厂修理情况,发现导弹中的转换开关、稳压器、电源组件、陀螺仪等部件失效是整弹贮存失效的关键因素[22]。因此,选定这4个部件作为评估整弹健康状态的关键部件。根据电子产品技术特点,选定特征电压作为上述部件的关键性能参数。通过定期测试贮存期内导弹关键部件的特征电压来估计出整弹退化程度。因此,导弹的失效时间T可表示为
T=min{Td,Tr}
(1)
式中,Td为导弹退化失效时间,可通过整弹退化程度数据估计出;Tr为导弹突发失效时间。
则在退化失效与突发失效的相关性竞争失效场合下,贮存期(0,t]内导弹可靠度R(t)可表示为
R(t)=P{T>t}=P{Td>t,Tr>t}=
P{Tr>t|Td>t}·P{Td>t}=Rr|d(t)·Rd(t)
(2)
式中,Rr|d(t)表示未发生退化失效条件下Tr的条件可靠度;Rd(t)为Td的可靠度。
导弹平均寿命ξ可表示为

(3)
2 多元退化失效建模
用弹上多个关键部件特征电压数据来推断出整弹退化状态,可视为多元退化建模问题,其处理思路是先将多维部件特征电压转化为一个整弹退化参数,然后采用一元随机过程模型对转化后整弹退化程度数据进行退化建模。
2.1 将多部件特征电压转化为整弹退化参数
将引入状态空间模型[8],利用弹上关键部件的特征电压的定期测试数据来构建整弹状态特征矩阵,通过计算整弹正常状态与当前退化状态之间相似程度,得到整弹的退化程度。
(1)构建状态特征矩阵
将测试得到的弹上关键电子产品的特征电压作为其状态信息,构建特定状态下导弹的状态特征矩阵,表达式为
(4)
式中,X为状态特征矩阵;xj=(x1j,x2j…,xnj)T为特征矢量;xij为第i(i=1,2,…,n)个特征在时刻j(j=1,2,…,m)的状态数据;n为特征个数;m为测试点个数。
(2) 建立状态子空间
正常状态与退化状态下,导弹的状态特征矩阵所蕴含的状态信息不同,表现在两种状态下的导弹状态子空间存在一定的差异。采用核主成分分析法,从状态特征矩阵中建立状态子空间,具体如下:
利用非线性映射φ(·),将状态特征矩阵X映射到高维特征空间F中,即
Xaφ(·):
φ(X)=[φ(x1),φ(x2),…,φ(xm)]
(5)
式中,φ(X)表示F中状态特征矩阵;φ(xj)(j=1,2,…,m)表示对应于特征矢量xj的非线性特征矢量。
核主成分分析的特征方程为
mhα=Kα
(6)
式中,α为权向量;h为φ(X)的协方差矩阵C的特征值;K为核矩阵,其定义如下:
Kij=〈φ(xi),φ(xj)〉=k(xi,xj)
(7)
式中,i,j=1,2,…,m;k(·)为核函数。
本文采用高斯核函数,形式为
(8)
由式(6)计算出权向量α。
将协方差矩阵C的特征向量δ归一化处理,得到其正交基向量ω,表达式为
(9)
选择较大的特征值h所对应的ω,建立状态子空间S,即
S=span(ω1,ω1,…,ωr)
(10)
式中,r为状态子空间维数。
(3) 计算子空间主夹角
设正常状态下导弹的状态子空间为S0,退化状态下导弹的状态子空间为S1,则S0与S1之间的相似性可通过子空间正交基向量之间的主夹角表示。主夹角越大,两者之间的相似性越小。将基向量内积矩阵记为W,表示为
(11)
对(11)进行奇异值求解,得到d个特征值κ1,κ2,…,κd,则主夹角θi表示为
θi=arccosκi,i=1,2,…,d
(12)
(4) 计算整弹退化程度
由式(12)可知,θi∈[0,π/2],θi越大,说明S0与S1之间的相似性越小,导弹性能退化程度越大。由于最小的主夹角反映了两个子空间最主要的相似性信息,因此将整弹退化程度Y定义为最小主夹角的正弦值,表示为
Y=sin[min(θi)]
(13)
2.2 退化模型
将导弹的退化程度Y(t)看作成一个随机变量,拟采用一元Wiener、Gamma和Inverse-Gaussian过程进行退化建模。
假设Y(t)服从Wiener过程,即
Y(t)=Y(0)+uΛ(t)+σB(Λ(t))
(14)
式中,u为漂移系数;σ为扩散系数;B(·)为标准布朗运动;Λ(t)为时间t的函数,表征Y(t)在时间轴上的非线性特征;Y(0)为初始退化量,不失一般性情况下,令Y(0)=0。
根据Wiener过程性质,独立平稳增量ΔY(t)服从正态分布,即ΔY(t)~N(uΔΛ(t),σ2ΔΛ(t)),其中ΔY(t)=Y(t+Δt)-Y(t);ΔΛ(t)=Λ(t+Δt)-Λ(t),则Y(t)的概率密度函数(probability density function, PDF)为
(15)
设Y(t)退化失效阈值为D,Y(t)首次达到D的时间TD定义为TD=inf{t|Y(t)≥D},则TD服从Inverse-Gaussian分布,可推导出TD的可靠度函数为
(16)
当Y(t)服从Gamma过程,则ΔY(t)服从Gamma分布,即ΔY(t)~Ga(uΔΛ(t),σ),其中u,σ分别为形状参数和尺度参数,则Y(t)的概率密度函数为
(17)

同理推导出TD的可靠度函数为
(18)

当Y(t)服从Inverse-Gaussian过程,则ΔY(t)服从Inverse-Gaussian分布,即ΔY(t)~IG(uΔΛ(t),σΔΛ(t)2),其中u,σ分别为均值和尺度参数,则Y(t)的PDF为
(19)
同理推导出TD的可靠度函数为
(20)
2.3 参数估计
现有M枚导弹进行定期测试,测试时刻tij(i=1,2,…,M;j=1,2,…,Mi)处的退化程度记为Y(tij)。不失一般性情况下,令上述退化模型中Λ(t)=tc(c>0为待定常数),将未知参数集合记为θ1=(u,σ,c)。根据Y(t)的PDF,建立整弹退化程度数据样本的似然函数如下:
(21)
若Y(t)服从Wiener过程,将式(15)代入式(21),可得
(22)
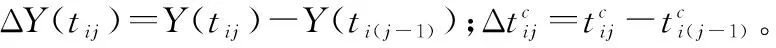
分别令式(22)关于u,σ2的一阶偏导数为零,求得u,σ2的极大似然估计:
(23)
(24)
由于式(23)、式(24)的求解依赖于c的取值,采用两步极大似然估计法[23],借助Matlab软件中的fminsearch函数可解决此问题。


当Y(t)服从Gamma过程和Inverse-Gaussian过程时,同理求解出θ1估计值以及对应的lnL(θ1)值。将赤池信息准则(Akaike information criterion,AIC)作为选择Y(t)的随机过程类型的判断准则,即将AIC取最小值所对应的随机过程作为Y(t)的最优随机过程类型。其计算公式为
AIC=2p-2lnL(·)
(25)
式中,p为未知参数个数。
3 突发失效建模
3.1 突发失效模型
导弹为典型的机电一体化产品,一般认为其突发失效时间Tr服从双参数威布尔分布,则不考虑性能退化影响的突发失效率函数λr0(t)为
(26)
式中,m为形状参数;η为尺度参数。
采用比例危险模型[19],描述突发失效率与时间、整弹退化程度之间的正相关函数关系。假设到时刻t时导弹仍未失效,此时导弹突发失效率记为λr[t,Y(t)],可表示为
λr[t,Y(t)]=λr0(t)·q(Y(t))
(27)
式中,λr0(t)为q(Y(t))=1时的标准危险函数;q(Y(t))≥1为比例系数,其常用函数形式为q(Y(t))=exp(βY(t)),其中β为待定系数。
为保证t时刻导弹不发生退化失效(即未达到失效阈值D),将式(27)改写为

(28)
在未发生退化失效条件下Tr的条件可靠度函数和条件PDF分别为

(29)
fr|d(t)=λr[t,Y(t)]·Rr|d(t)
(30)
3.2 参数估计
现有N枚导弹发生突发失效,突发失效时刻分别记为t1,t2,…,tN,对应的退化程度分别记为Y(t1),Y(t2),…,Y(tN)。将上述模型中未知参数集合记为θ2=(m,η,β)。根据fr|d(t),建立导弹突发失效样本的似然估计函数为
(31)
对于上述似然函数同样是采用两步极大似然估计法进行求解,即先确定β,再求解m,η。
4 实例分析
已知现有一批16枚某型导弹,贮存期为8年,每半年测试弹上转换开关、稳压器、电源组件、陀螺仪这4个关键产品的特征电压情况。其中,一组弹上关键部件特征电压数据如表1所示。根据导弹设计规范,当部件的特征电压值漂移量超过±10%时,则判定为退化失效;当部件的特征电压为0或者超过1倍,则判定导弹突发失效。
为便于对比分析,将本文提出的退化失效与突发失效之间相关的竞争建模方法记为M1;将退化失效与突发失效之间独立的竞争建模方法记为M2;将仅考虑退化失效建模方法记为M3。

表1 某导弹关键部件的特征电压值
4.1 整弹退化程度计算
根据失效判据可知,在测试期内这批导弹中有6枚导弹发生突发失效,采用状态空间模型,计算出突发时间时整弹退化程度值如表2所示。

表2 导弹突发失效时的退化程度
采用状态空间模型,计算出余下10枚整弹退化程度数据如图1所示。根据退化失效判据,计算出导弹退化失效时的整弹退化程度值为4.120,即失效阈值D。由此可知,这10枚导弹中有3枚导弹退化失效(图1中蓝线退化轨迹),失效时间分别为7、8、8年。

图1 10枚整弹退化程度数值曲线Fig.1 Ten missiles degradation degree value curves
4.2 参数估计结果
依据10枚整弹退化程度数据,给定θ1中参数c的初值为1.10,利用fminsearch函数,对式(21)进行遍历搜索,得到参数估计结果如表3所示。

表3 退化模型参数估计结果
由表3可以看出,Y(t)服从Wiener过程时,计算出的AIC值最小,说明Y(t)最优随机过程类型是Wiener过程。经置信水平为0.95的正态分布假设检验,接受整弹退化程度增量ΔY(t)服从正态分布的结论,进一步说明整弹退化程度服从Wiener过程是可信的。
依据6枚导弹突发失效时间及对应的退化程度数据,给定θ2中参数β的初值为0.25,利用fminsearch函数,对式(31)进行遍历搜索,得到参数估计结果为
(32)
经置信水平为0.95的威布尔分布假设检验,接受导弹突发失效时间服从威布尔分布的结论。
4.3 贮存寿命评估分析
根据上述参数估计值,由式(2)计算出竞争失效场合下导弹贮存可靠性函数R(t),绘制出不同方法下导弹贮存可靠度曲线如图2所示。与M2、M3的可靠度曲线相比,M1的可靠度曲线偏保守,符合工程上的做法。

图2 3种方法下可靠度曲线Fig.2 Reliability curve by three methods
根据这批导弹所记录的失效时间或截尾时间,计算出这批导弹的贮存寿命统计值,即
式中,Tr,Td,tn分别为突发失效时间、退化失效时间、测试截止时间;rr,rd分别为突发、退化失效数。
实际上,由于导弹失效时间应该是介于当前测试失效时间与上一次测试时刻之间,因此ξ*值应在[12.61,13.11]。
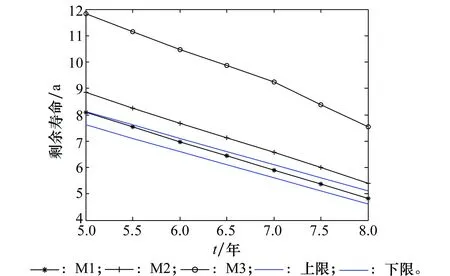
图3 不同方法下导弹贮存剩余寿命值Fig.3 Missile storage remaining life by different methods
5 结 论
(1)引入状态空间模型,将多维部件特征电压转化为一维整弹退化参数,采用多个随机过程模型对整弹退化程度数据进行拟合,将AIC值最小所对应的随机过程模型作为其最优选择,能较好地拟合整弹退化程度的退化特征;
(2)采用比例危险模型,建立了考虑整弹退化程度影响的导弹突发失效模型,能客观描述导弹性能退化对其突发失效的影响;
(3)采用两步极大似然估计法,借助fminsearch函数,求解出模型中多个参数估计值,为解决参数个数多于方程组个数的参数估计问题提供了一种可行途径。
(4)结合某批次导弹贮存实例,评估了导弹的平均寿命与剩余寿命值,并与现有方法的评估结果进行了对比分析,进一步证实了本文所提出方法具有较好的评估精度,具有一定的工程应用价值。
参考文献:
[1] 罗湘勇,黄小凯.基于多机理竞争退化的导弹贮存可靠性分析[J].北京航空航天大学学报,2013, 39(5): 701-705.
LUO X Y, HUANG X K. Storage reliability analysis of missile based on multi-mechanism competition degradation method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 701-705.
[2] LUO W, ZHANG C H, CHEN X, et al. Accelerated reliability demonstration under competing failure modes[J]. Reliability Engineering and System Safety, 2015, 136: 75-84.
[3] CHEN Y, ZHANG Q, CAI Z, et al. Storage reliability assessment model based on competition failure of multi-components in missile[J]. Journal of Systems Engineering and Electronics, 2017, 28(3): 606-616.
[4] WANG X L, BALAKRISHNAN N, GUO B, et al. Residual life estimation based on bivariate non-stationary Gamma degradation process[J]. Journal of Statistical Computation and Simulation, 2015, 85(2): 405-421.
[5] WANG X L, GUO B, CHENG Z J, et al. Residual life estimation based on bivariate wiener degradation process with measurement errors[J]. Journal of Central South University, 2013, 20(7): 1844-1851.
[6] 王华伟, 高军, 吴海桥. 基于竞争失效的航空发动机剩余寿命预测[J]. 机械工程学报, 2014, 50(6): 197-204.
WANG H W, GAO J, WU H Q. Residual remaining life prediction based on competing failures for aircraft engines[J]. Journal of Mechanical Engineering, 2014, 50(6): 197-204.
[7] 王浩伟, 奚文骏, 冯玉光. 基于退化失效与突发失效竞争的导弹剩余寿命预测[J]. 航空学报, 2016, 37(4): 1240-1248.
WANG H W, XI W J, FENG Y G. Remaining life prediction based on competing risks of degradation failure and traumatic failure for missiles[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1240-1248.
[8] 孙闯, 何正嘉, 张周锁, 等. 基于状态信息的航空发动机运行可靠性评估[J]. 机械工程学报, 2013, 49(6): 30-37.
SUN C, HE Z J, ZHANG Z S, et al. Operating reliability assessment for aero-engine based on condition monitoring information[J]. Journal of Mechanical Engineering, 2013, 49(6): 30-37.
[9] CONG H, WU G P, FENG F Z. Reliability assessment of a certain diesel engine with multi-parameter degradation based on SVM[J].Advanced Materials Research,2011,291(7):2164-2167.
[10] LOUTAS T H, ROULIAS D, GEORGOULAS G. Remaining useful life estimation in rolling bearings utilizing data-driven probabilistic e-support vectors regression[J]. IEEE Trans.on Reliability, 2013, 62(4): 821-832.
[11] PAN Z Q, BALAKRISHNAN N, SUN Q, et al. Bivariate degradation analysis of products based on Wiener processes and copula[J]. Journal of Statistical Computation and Simulation, 2013, 83(7): 1316-1329.
[12] ZHANG X P, SHANG J Z, CHEN X, et al. Statistical inference of accelerated life testing with dependent competing failure based on copula theory[J]. IEEE Trans.on Reliability, 2014, 63(3): 764-778.
[13] PAN Z Q, BALAKRISHNAN N, SUN Q, et al. Bivariate degradation analysis of products based on Wiener processes and copulas[J]. Journal of Statistical Computation and Simulation, 2013, 83(7): 1316-1329.
[14] 王浩伟,滕克难,李军亮.随机环境冲击下基于多参数相关退化的导弹部件寿命预测[J].航空学报,2016,37(11):3404-3412.
WANG H W, TENG K N, LI J L. lifetime prediction for missile components based on multiple parameters correlative degradation with random shocks of environmental stresses[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3404-3412.
[15] 钟强晖, 张志华, 梁胜杰. 基于多元退化数据的可靠性分析方法[J]. 系统工程理论与实践, 2011, 31(3): 544-551.
ZHONG Q H, ZHANG Z H, LIANG S J. Reliability analysis approach based on multivariate degradation data[J]. Systems Engineering Theory & Practice, 2011, 31(3): 544-551.
[16] JIANG L, FENG Q, COIT D W. Reliability and maintenance modeling for dependent competing failure processes with shifting failure thresholds[J].IEEE Trans.on Reliability,2012,61(4): 932-948.
[17] SU C, QU Z Z, HAO H B. Reliability assessment considering dependent competing failure process and shifting-threshold[J]. Journal of Southeast University, 2013, 29(1): 52-56.
[18] SU C, ZHANG Y, ZHANG H. Product reliability assessment based on proportional hazard degradation model[J]. Journal of Southeast University, 2010, 26(3): 480-483.
[19] 蔡忠义,陈云翔,张诤敏,等.基于比例失效率退化模型的可靠性评估方法[J].系统工程与电子技术,2015,37(8):1943-1947.
CAI Z Y, CHEN Y X, ZHANG Z M, et al. Method on reliability assessment based on proportional failure rate degradation model[J]. Systems Engineering and Electronics, 2015, 37(8): 1943-1947.
[20] 丛林虎,徐廷学,王骞,等.基于退化数据与故障数据的导弹竞争故障预测[J].北京航空航天大学学报,2016,42(3):522-531.
CONG L H, XU T X, WANG Q, et al. Missile competing fault prediction based on degradation data and fault data[J]. Journal Beijing University of Aeronautics and Astronautics, 2016, 42(3): 522-531.
[21] LEHMANN A. Joint modeling of degradation and failure time data[J]. Journal of Statistical and Inference, 2009, 139(5): 1693-1706.
[22] 孟涛,张仕念,易当祥,等.导弹贮存延寿技术概念[M].北京:中国宇航出版社,2013:45-50.
MENG T, ZHANG S N, YI D X, et al. Life extension technology generality of missile storage[M]. Beijing: China Aerospace Press, 2013: 45-50.
[23] CAI Z Y, CHEN Y X, ZHANG Q, et al. Residual lifetime prediction of nonlinear step-stress accelerated degradation data with measurement error[J]. Journal of Systems Engineering and Electronics, 2017, 28(5): 1028-1038.
