现代有轨电车与常规公交运营组织协调策略

陈维亚，巩宇鹏，陈治亚，宋晓东

(中南大学 交通运输工程学院，湖南 长沙 410075)

现代有轨电车以其投资省、建设快、中运量、亲环境、灵活性较大等特点重新进入现代城市公共交通系统，并与常规公交组合发展成为一种新的公交系统模式[1]。在该系统模式下，现代有轨电车与常规公交运营组织的协调优化问题成为重要的研究内容[2]。针对现代有轨电车与常规公交的协调优化主要包括二者的规划设计协调和运营组织协调两个方面。前者主要关注有轨电车与常规公交线网的规划设计协调，胡军红等[3]针对城市新区有轨电车线网的规划设计；后者主要关注有轨电车与常规公交的运营调度协调，它是保证系统运行目标的主要技术。当前针对轨道交通(如地铁)与常规公交运营调度协调的研究较多，提出的研究方法主要是解决如何建立协调时刻表问题[4−9]，而专门针对现代有轨电车与常规公交运营调度协调的研究正在逐步深入[10−11]。现代有轨电车与地铁等其他城市轨道交通系统在运营组织上具有差异性(如路权专有性)，因此，本文专门针对现代有轨电车与常规公交的调度协调问题，提出了一种基于换乘的现代有轨电车与常规公交的运营调度协调策略模型。通过模型，可获得现代有轨电车与常规公交的协调策略参数及最优系统行车间隔。

1 问题分析

1.1 现代有轨电车与常规公交调度协调的内涵

根据公共交通运营调度控制理论[12]，多种运输模式或多条线路运营组织的调度协调可分为静态调度协调和动态调度协调2个层面。静态调度协调，即行车计划协调，或称静态时刻表协调；动态调度协调，主要是选择并实施动态协调控制策略或参数。不管是静态还是动态调度协调，多种模式或多条线路之间的协调落脚点是运能匹配下的换乘协调问题[13]。

基于换乘的现代有轨电车与常规公交的调度协调问题可描述为在运能匹配等约束条件下，在保障系统运行目标的前提下，实现乘客在有轨电车与常规公交中的换乘连续性和顺畅性。此处，换乘的连续和顺畅是指乘客在由一种交通方式到达换乘站后，在短时间内可以换乘至另一种交通方式[5]。相较于常规公交，现代有轨电车具有运量较大但线路灵活性较低的特点。因此，常规公交通常发挥为现代有轨电车集散乘客的作用，在进行两者的协调调度时，需要使得常规公交调度尽量配合有轨电车行车计划，以降低换乘乘客的换乘时间和等候时间，确保乘客换乘的顺畅性和连续性。

1.2 现代有轨电车与常规公交的换乘协调关系

在现代有轨电车与常规公交的系统中，乘客在换乘站的换乘时间受到线路交叉形式、有轨电车线路敷设方式、有轨电车及常规公交到站时间分布、个人行走习惯等因素的影响。不失一般性，本文研究一条有轨电车线路与多条常规公交线路呈穿越式布局的公共交通系统，有轨电车线路敷设方式为半独立路权路中布局及路肩两侧布局混合式。与地下轨道交通方式不同，现代有轨电车占用道路资源，无完全独立路权情况下有轨电车车辆到站时间具有不确定性，本文假设有轨电车到站服从正态分布ftram(atram)。

常规公交作为接运公交，发挥为有轨电车集散乘客功能。但常规公交运行受道路交通状况影响更为显著。本文假设常规公交到站服从正态分布fBi(aBi)。在研究有轨电车与常规公交的运营组织协调时，本文定义有轨电车与常规公交到站时间间隔为φi，两者运营组织协调策略参数为ξi，且。即对有轨电车与常规公交的到站时间间隔参数进行控制，通过该参数可使得常规公交相较于有轨电车提前或推后一段时间到站，以保证乘客可以顺畅换乘。

以下针对不同敷设方式条件下有轨电车与常规公交的换乘关系进行具体分析。

1.2.1 路中布局式有轨电车与常规公交的换乘

在半独立路权的有轨电车系统中，路中布局方式是指现代有轨电车双线集中敷设于道路中央，利用中央分隔带及机动车道改造而成，机动车及非机动车道布设于有轨电车两侧[14]，如图1所示。

路中布局方式现代有轨电车与常规公交之间的换乘关系如图2所示。

图1 现代有轨电车路中布局方式示意图Fig. 1 Road-middle designed modern tram

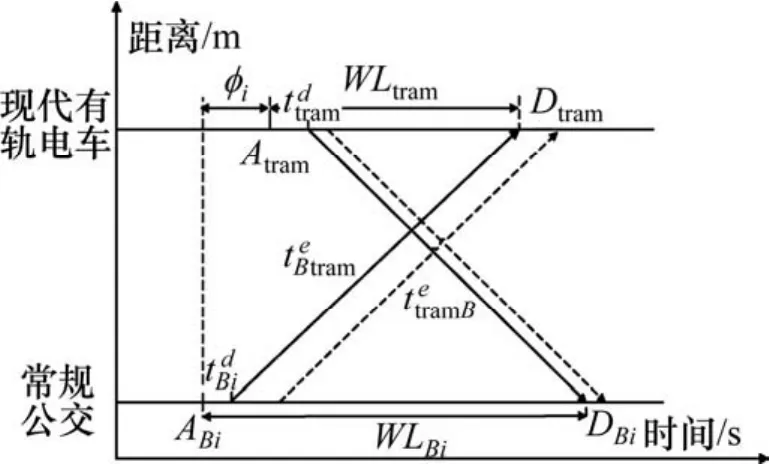
图2 路中布局式现代有轨电车与常规公交换乘时空示意图Fig. 2 Transfer rule of time and space for the road-middle tram and the bus

图2 中，常规公交在期望时间ABi到站，有轨电车在期望时间Atram到站，两者到站间时间间隔为φ。乘客通过td走下常规公交，并通过时间换乘至有轨电车车站，若此时现代有轨电车尚未驶离车站，乘客可顺利登上有轨电车，此时称之为常规公交换乘有轨电车换乘成功，否则成为换乘失败。同理可得有轨电车乘客换乘常规公交时换乘成功和失败的条件。因此，路中式现代有轨电车与常规公交换乘协调关系可总结如表1所示。

表1 路中式现代有轨电车与常规公交换乘关系Table 1 Transfer-rule for the road-middle tram and the bus

1.2.2 路肩两侧式布局方式有轨电车与常规公交的换乘关系

相比于路中式，路肩两侧布局方式是指有轨电车设于道路两侧边缘的机动车道上，站台置于机动车道与非机动车道的分隔带上[14]，如图3所示。

路肩两侧布局方有轨电车与常规公交之间的换乘关系如图4所示。

图3 现代有轨电车路肩两侧布局方式示意图Fig. 3 Road-shoulder designed modern tram

图4 路肩两侧式现代有轨电车与常规公交换乘时空示意图Fig. 4 Transfer rule of time and space for the road-shoulder tram and the bus

图4 中，两者客流直接汇集于换乘站台。对于有轨电车换乘常规公交的乘客，有轨电车在常规公交离站前到达，即可实现换乘成功，反之则换乘失败；对于常规公交换乘有轨电车的乘客，常规公交在有轨电车离站前到达，即可实现换乘成功，反之则换乘失败。路肩两侧式现代有轨电车与常规公交(共站)的换乘协调关系如表2所示。

表2 路肩两侧式现代有轨电车与常规公交换乘协调关系Table 2 Transfer-rule for the road-shoulder tram and the bus

根据有轨电车与常规公交换乘成功的条件可知，有轨电车与常规公交的实际到站时间是换乘成功的关键。因此，在调度协调下，可通过对两者的到站时间间隔进行控制，即通过决策协调策略参数iξ，以增加乘客换乘成功的概率。但协调策略参数iξ可能会造成公交车辆的停站时间过长，使非换乘乘客的出行时间成本增加。同时，还可能带来因公交车辆周转时间的增大而带来运营成本的增加。因此，必须在考虑运营成本的前提下，合理设置两者运营组织协调控制参数。

2 现代有轨电车与常规公交运营组织协调模型

2.1 模型目标及参数

现代有轨电车与常规公交的运营组织协调最终目的在于提高系统协调运行效率，降低系统成本。因此，本文所构建的有轨电车与常规公交运营组织协调模型的目标是在有轨电车与常规公交的运能匹配约束下，保证乘客协调换乘情况下实现系统成本最小，并可通过模型获得协调控制参数值和最优行车间隔。

本文研究的系统成本为系统广义成本，包括乘客出行成本和系统运营成本[6−9]。其中，乘客出行成本主要指乘客的步行时间成本、候车时间成本、在车时间成本和换乘时间成本。系统运营成本主要指在满足相关目标运输能力约束下的有轨电车和常规公交的运营成本。系统广义成本表示如下：

式中：C，Co和Cu分别为系统广义成本、运营成本和乘客出行成本，α和β为权重系数。

2.1.1 乘客出行成本

乘客出行成本理论上包括乘客的步行时间成本、候车时间成本、在车时间成本和换乘时间成本。乘客的步行时间成本受到乘客起讫点与公共交通车站距离的影响。在公共交通系统规划设计过程中，针对某特定公共交通车站，其覆盖半径固定，因此乘客出行起讫点至公共交通车站的平均用时可认定为常量；同时，假定公交运行的平均速度也不发生显著改变的情况下，乘客的在车时间成本也可视为常量，不影响系统成本的优化。因此，本文所考虑的乘客出行成本主要是指乘客的候车时间成本和换乘时间成本，即：

其中：Cuh和Cue分别表示乘客候车时间成本和乘客换乘时间成本(元)，它们受到是否采取有轨电车与常规公交协调运营组织策略的影响。乘客候车时间成本Cuh指乘客在选乘公共交通工具出行时，第一次登上公共交通工具前所需的等待时间。需要明确的是，此部分候车时间不包括乘客在换乘公共交通工具时所用等待时间。在本文研究范围内，乘客候车时间包括乘客第一次到达有轨电车站后等待时间 Thtram和第一次到达常规公共交通车站后等待时间ThB。即可表示为：

式中：Cuh为乘客候车总时间成本，元；Chtram为有轨电车乘客候车时间成本，元；ChB为常规公交乘客候车时间成本，元；为有轨电车在方向 d站点 j的候车客流，人/h；为常规公交线路 i在有轨电车站点j的候车客流，人/h；θj为有轨电车线路在方向 d站点 j上车的非换乘乘客比例；θBij为常规公交线路i在站点j上车的非换乘乘客比例；Thtram为有轨电车乘客在站点的平均等候时间，min；ThBi为常规公交线路i乘客在站点的平均等待时间，min；μp为乘客出行时间价值系数，元/min；m为常规公交线路数；n为有轨电车车站数。

其中，乘客在公共交通站点的平均等待时间按照 Welding提出的平均候车时间计算方法[15]计算，即：

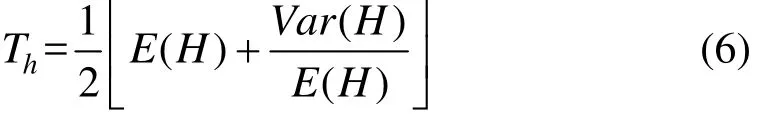
式中：E(H)为公共交通工具发车间隔均值，min；Var(H)为公共交通工具发车间隔方差，min。

乘客换乘时间成本Cue是有轨电车与常规公交运营组织协调的重点参数。在换乘站，有轨电车与常规公交可能存在多种换乘形式，即乘客在有轨电车之间、有轨电车与常规公交之间和常规公交之间的换乘。与此同时，有轨电车与常规公交是否进行运营组织协调直接影响乘客换乘成本的大小。本文研究为单条有轨电车线与多条常规公交线在不同换乘站的运营组织协调优化，因此，主要考虑乘客在有轨电车与常规公交之间的换乘成本。按照未实施运营组织协调和实施运营组织协调2种情况进行分析。

1) 未实施运营组织协调情况

在有轨电车与常规公交运营组织中未实施协调的情况下，乘客的换乘时间成本为：

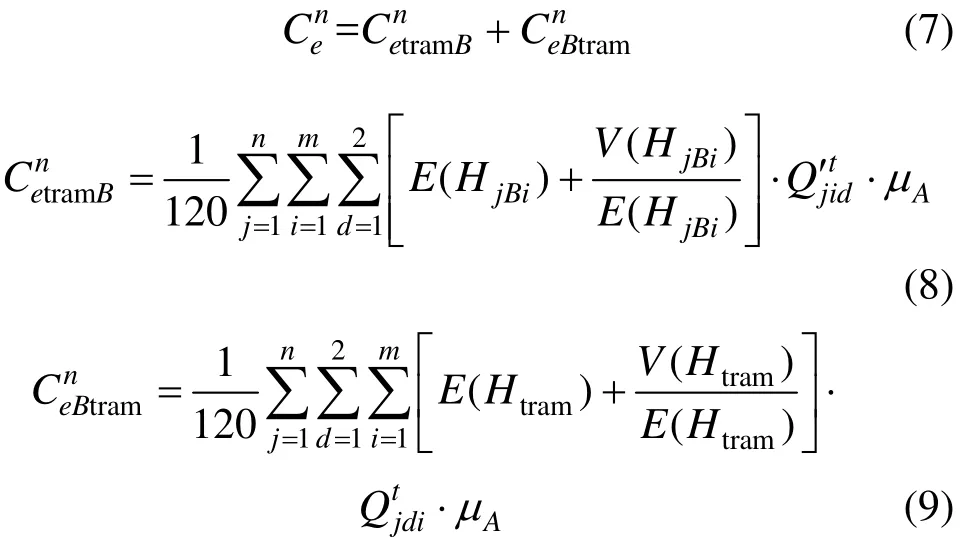
2) 实施有轨电车与常规公交运营组织协调

如前所述，运营组织协调主要通过协调参数iξ进行控制。在有轨电车与常规公交协调运营组织条件下，有轨电车与常规公交的换乘成功是指乘客在换乘站可以顺利换乘至当班公共交通车辆上。有轨电车与常规公交换乘时间成本可以表示为:

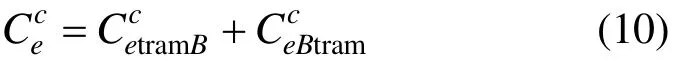
根据前文换乘关系分析，常规公交换乘有轨电车的时间成本可表示为式(11)，但是有轨电车乘客换乘常规公交的最小换乘时间需根据有轨电车线路敷设方式的不同进行个别计算，分别表示为式(12)和(13)。

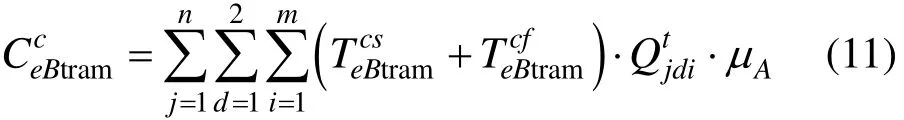
常规公交换乘路中式现代有轨电车的最小换乘时间为：

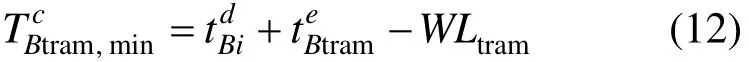
常规公交换乘路肩两侧式现代有轨电车(共站)的最小换乘时间为：

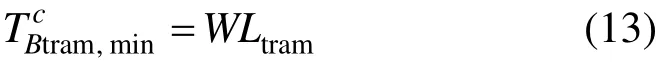
则此条件下常规公交换乘现代有轨电车成功及失败的期望换乘时间为：

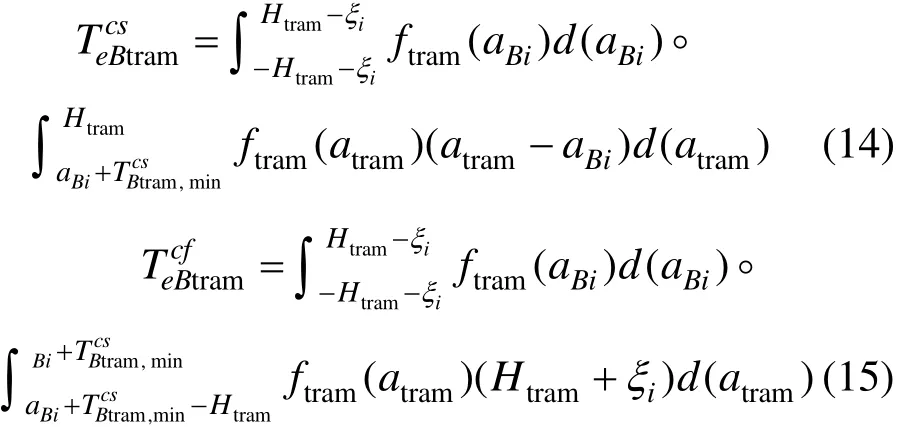
同理，有轨电车换乘常规公交的时间成本可表示为式(16)。

路中式现代有轨电车换乘常规公交的最小换乘时间为：

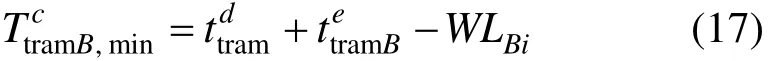
路肩两侧式现代有轨电车(共站)换乘常规公交的最小换乘时间为：

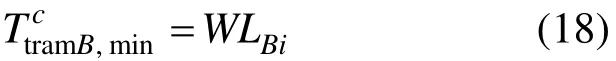
则此条件下现代有轨电车换乘常规公交成功及失败的期望换乘时间为：

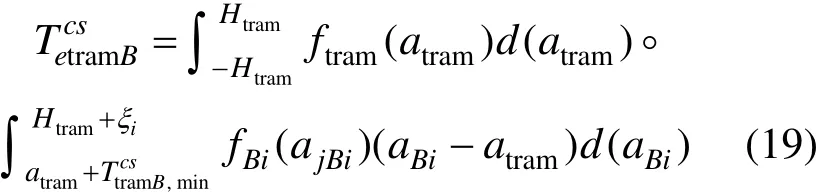
2.1.2 系统运营成本

系统运营成本包含车辆运营维护、人员管理等多方面成本。为了简化问题且不失一般性，将各类成本折算为公共交通车辆运营的单位距离成本，并将其视为定值。此时，系统运营成本将主要受到投入运营的车辆数和实际运行距离等因素相关，而投入运营的车辆数主要受到运能的约束，分析如下。

满足客流需求的有轨电车及常规公交车辆配置数为：

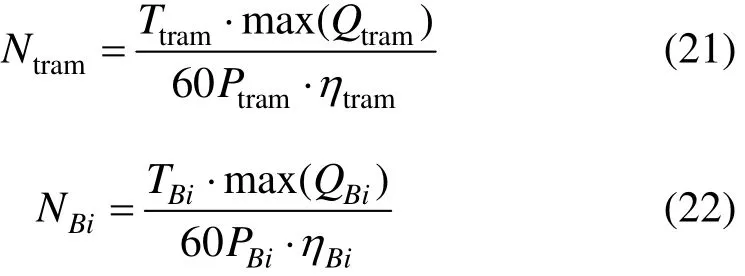
式中：Ttram和TBi为有轨电车线路及常规公交线路i全程运行损耗时间，min；Qtram和QBi为有轨电车线路及常规公交线路 i单向断面客流量，人；Ptram，PBi为有轨电车车辆及常规公交车辆的单列(辆)定员人数，人；ηtram和ηBi为有轨电车线路及常规公交线路i的计划满载率。

当考虑有轨电车与常规公交协调运营组织时，两者的运能必须匹配，常规公交车辆数量还需满足：

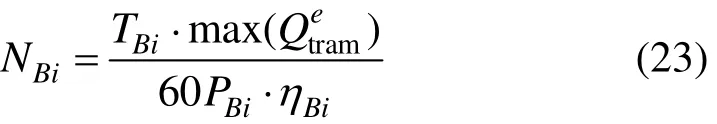
因此，有轨电车和常规公交的运营成本可以表示为：

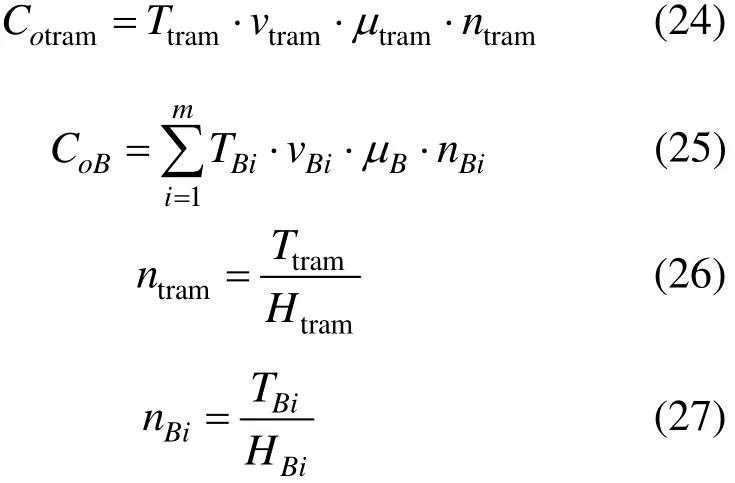
式中：ntram和nBi为有轨电车及常规公交的车辆数，辆；vtram和vBi为有轨电车及常规公交线路i的平均运行速度，km/h；μtram和μB为有轨电车及常规公交的单位距离运营成本系数，元/km；其中，ntram和nBi需要分别满足各自客流需求且不高于实际运营车辆配置数和，即：

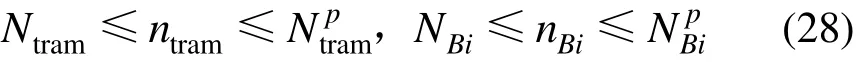
由此可得，考虑运能情况下的Htram和HBi约束条件：

2.2 优化模型

由以上分析可知，由于是否采取协调策略对成本的计算有差异，因此，有轨电车与常规公交运营组织优化模型需根据是否采用协调策略而有所区别。

1) 未采用运营组织协调策略

该优化模型是以发车间隔为单一变量的优化问题，模型可表示为：

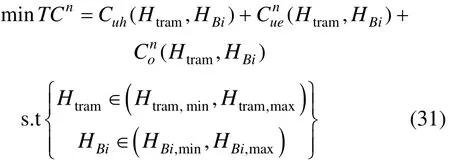
2) 采用运营组织协调策略

该模型是以系统发车间隔及运营组织协调控制参数为变量的多约束优化问题，模型可表示为：

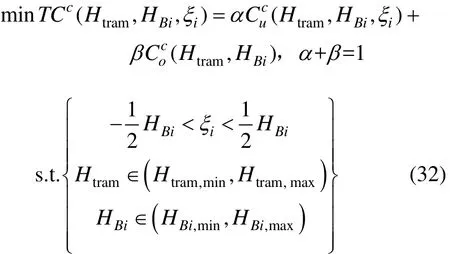
其中：对于实施运营组织协调的常规公交线路，HBi= Htram= H 。满足客流需求的有轨电车及常规公交线路车辆配置数量根据车辆定员和一定范围内的公共交通车辆满载率进行确定。通常，公共交通满载率取值区间为[0.7，1.2]，一列现代有轨电车定员为200~330人，常规公交按照90人/辆定员。

3 算例分析

3.1 算例数据

分析算例为一条有轨电车线路与多条穿越型常规公交线路所组成的公共交通系统。其中，有轨电车线路敷设方式为半独立路权下路中布局方式和路肩两侧布局方式混合型。即，有轨电车线路在部分路段为路中布局方式，在部分路段为路肩两侧布局方式并与常规公交并站。1~8站为有轨电车车站，其中2，4，6和8为有轨电车与常规公交换乘站，1~3站为有轨电车路肩两侧线路敷设方式，有轨电车与常规公交共站；4~8站为有轨电车路中布局线路敷设方式。算例线网如图5所示。

在参考相关城市实际运营统计数据的基础上，算例输入包括客流量、公共交通车辆站点停站时间等参数。具体见表3。

图5 有轨电车与常规公交线网算例示意图Fig. 5 Net-work of the modern tram and bus in the numerical example

表3 算例输入参数Table 3 Input of the numerical example

3.2 算例结果与分析

1) 未实施有轨电车与常规公交运营组织协调的优化结果

未实施有轨电车与常规公交运营组织协调条件下的系统模型为有轨电车和常规公交的发车间隔为变量的优化问题，用解析的方法求解模型。即求解：

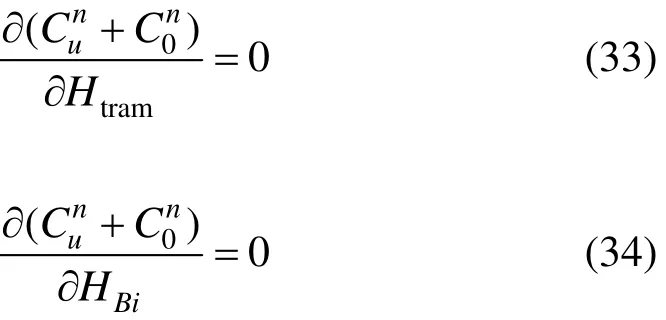
从模型的计算结果来看，实施有轨电车与常规公交运营组织协调可显著降低乘客的换乘成本，其次是候车成本，同时，因为对有轨电车与常规公交实施协调控制，导致运营成本小幅度增加，但二者所组成的系统成本降低，有轨电车与常规公交运营组织协调起到预期效果。

由此可解得未采用运营组织协调策略条件下的系统最优发车间隔如表4所示。

2) 实施有轨电车与常规公交运营组织协调的优化结果

实施有轨电车与常规公交运营组织协调模型为多变量优化问题，本文采用基于小生境思想的优化粒子群算法[16]对模型进行求解。由此求得有轨电车与常规公交运营组织协调控制参数iξ以及两者的最优发车间隔，如表4所示。

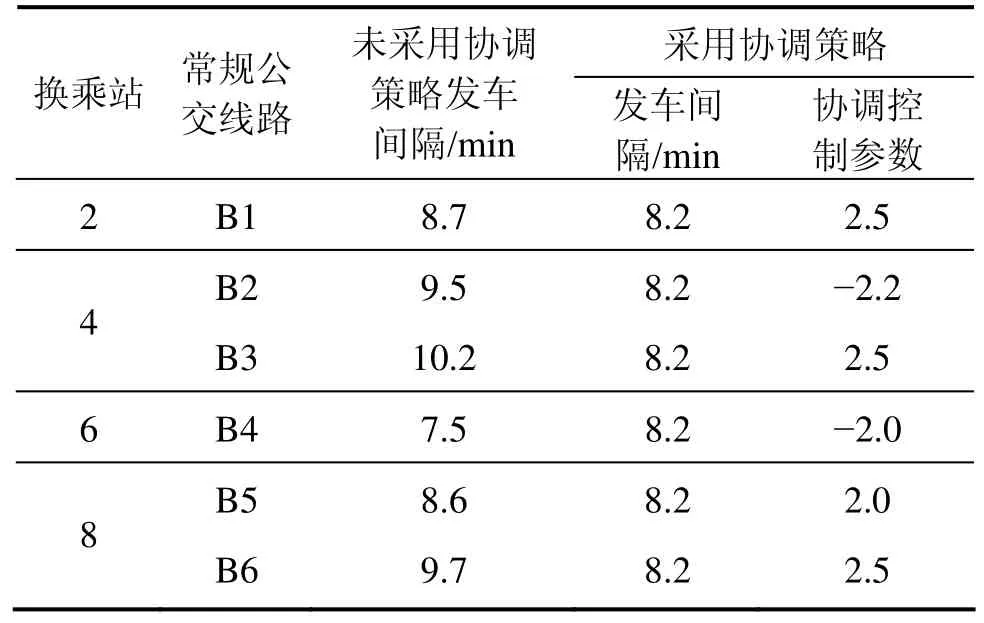
表4 采用/未采用协调控制策略条件下的最优解Table 4 Optimal solution under coordination operation strategy used/not used condition

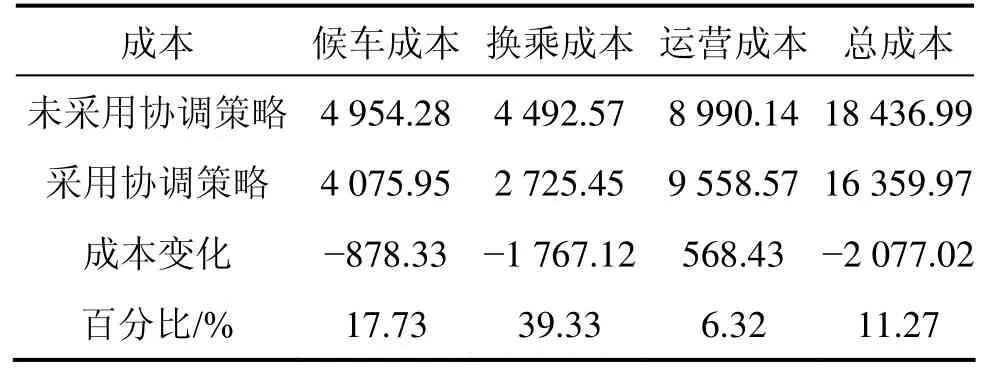
表5 未采用/采用协调策略下的公交系统广义成本对比Table 5 Compared general-cost of the transit system under coordination operation strategy used/not used condition 元

4 结论

1) 基于现代有轨电车及常规公交的技术经济特征，分析了现代有轨电车与常规公交所组成的新型城市公共交通系统运营组织协调的内涵，以换乘协调为落脚点，分析了路中式与路侧式2种敷设条件下的现代有轨电车与常规公交换乘协调关系。

2) 考虑系统运能匹配及约束，建立以有轨电车与常规公交系统总成本最小为目标的有轨电车与常规公交运营组织协调优化模型，通过解析求解可获得协调运营策略参数和系统最优行车间隔。

3) 基于换乘协调的有轨电车与常规公交运营组织协调策略参数可作为静态和动态协调调度的决策变量，为后期实现基于实时数据的协调调度控制提供决策基础。

参考文献：

[1] 赵野, 朱志国. 我国现代有轨电车功能定位的初探[J].交通运输工程与信息学报, 2016, 14(1): 70−75.ZHAO Ye, ZHU Zhiguo. Exploration on the modern tram function in our country[J]. Journal of Transportation Engineering and Information, 2016, 14(1): 70−75.

[2] 张海军, 胡军红, 杨敏, 等. 现代有轨电车最小发车间隔及相关指标研究[J]. 南京工业大学学报(自然科学版), 2016, 38(3): 107−113.ZHANG Haijun, HU Junhong, YANG Min, et al. Study on the minimum departure interval and relevant indexes of modern tram[J]. Journal of Nanjing Tech University(Natural Science Edition), 2016, 38(3): 107−113.

[3] 胡军红, 过秀成. 城市新区现代有轨电车线网规划方法研究——以南京河西新城为例[J]. 现代城市研究,2016(10): 73−78, 126.HU Junhong, GUO Xiucheng. Research on the planning method of modern tram network in new urban district: a case study of Nanjing Hexi new town[J]. Modern Urban Research, 2016(10): 73−78, 126.

[4] Mcbrayer D. Blurring the light rail transit-bus rapid transit boundaries[C]// 9th National Light Rail Transit Conference, 2003: 133−148.

[5] 何波. 城市轨道交通与常规公交运营协调优化技术研究[D]. 北京: 北京交通大学, 2009.HE Bo. Study on the coordination technology between urban rail system and bus system[D]. Beijing: Beijing Jiaotong University, 2009.

[6] Chien S, Schonfeld P. Joint optimization of a rail transit line and its feeder bus system[J]. Journal of Advanced Transportation, 1997, 31(3): 251−284.

[7] Ching J, Schonfeld P. Schedule coordination in a multiple hub transit network[J]. ASCE Journal of Urban Planning and Development, 2005, 131(2): 112−124.

[8] 林国鑫, 陈旭梅. 城市轨道交通与常规公交系统协调评价探讨[J]. 交通运输系统工程与信息, 2006, 6(3):89−92.LIN Guoxin, CHEN Xumei. Study on the evaluation of coordination between urban rail system and bus system[J]. Journal of Transportation Systems Engineering and Information Technology, 2006, 6(3): 89−92.

[9] Chien S. Optimization of coordinate intermodal transit networks[D]. Maryland: Maryland College Park, 1995.

[10] 卫超. 现代有轨电车的适用性研究[D]. 上海: 同济大学, 2008.WEI Chao. The study of modern tram system adaptability[D]. Shanghai: Tongji University, 2008.

[11] 张翔. 现代有轨电车适用性及其线网方案优选研究[D].北京: 北京交通大学, 2016.ZHANG Xiang. Study on the applicability of modern tram and its optimal selection of its network[D]. Beijing:Beijing Jiaotong University, 2016.

[12] 陈维亚. 基于智能技术的城市公交服务可靠性研究[D].长沙: 中南大学, 2010.CHEN Weiya. Transit service reliability under the framework of intelligent technologies[D]. Changsha:Central South University, 2010.

[13] 邓连波, 高伟, 赖天珍, 等. 基于换乘网络的城市轨道交通关联公交接驳线网优化[J]. 铁道科学与工程学报,2012, 9(6): 77−83.DENG Lianbo, GAO Wei, LAI Tianzhen, et al. Optimal design of feeder-bus network related to urban rail transit based on transfer network[J]. Journal of Railway Science and Engineering, 2012, 9(6): 77−83.

[14] 薛洪峰. 现代有轨电车信号控制关键技术研究[D]. 北京: 北京交通大学, 2013.XUE Hongfeng. Research on key technology of modern tram signal control[D]. Beijing: Beijing Jiaotong University, 2013.

[15] Welding P I. The instability of close interval service[J].Operation Research Quarterly, 1957, 8(3): 133−148.

[16] 王俊年, 申群太, 沈洪远, 等. 一种改进的小生境微粒群算法[J]. 山东大学学报(工学版), 2005, 35(3): 98−102.WANG Junnian, SHEN Quntai, SHEN Hongyuan, et al.A modified niching particle swarm optimization algorithm[J]. Journal of Shandong University(Engineering), 2005, 35(3): 98−102.