基于动态间隔时间的列车追踪策略研究

郑维耀，李茂青，江娜

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

列车自动驾驶系统(Automatic Train Operation ATO)要实现列车根据获得的线路信息和运营要求，结合列车实际的运行状态，自动调整列车的牵引/制动力，保证列车安全、高效运行。目前，通过ATO实现列车追踪运行，速度调整的思想为：由 ATO先生成一条平滑的速度期望曲线，再通过控制器采用智能算法控制列车按期望曲线运行。列车追踪运行策略反映在其速度调整时的期望曲线上。为此，有学者对ATO期望曲线的生成及优化进行了研究：Willian等[1]分析了目前 CBTC(Communications-Based Train Control)系统中能耗较大，并提出了一种模糊算法，利用惰行命令来提高列车运行的节能性，该方法只适用与地铁中；林颖等[2]从列车整个运行过程考虑，根据不同的运行指标给出了不同的ATO运行等级曲线，列车运行中根据不同的运行需求在不同的等级曲线间切换，实现了列车运行期望曲线的在线计算与优化，但该文献只考虑了一列车单独运行的情况，期望曲线的优化中没有考虑到线路中其他车辆对期望曲线的影响；GU等[3]考虑了追踪情况下列车能耗问题，提出了一个基于多模型的开关优化框架，以减少能源消耗；王鹏玲等[4]考虑了列车追踪时的安全因素，采用基于预测控制的分层控制来控制列车安全运行，上层控制器根据追踪运行状态生成期望加速度，下层控制器控制列车运行，使实际加速度和期望加速度保持一致，但该研究只考虑了当列车间间隔小于安全要求时后车采取相应策略，并未考虑让列车保持一定的追踪间隔运行；潘登等[5]根据公路跟驰模型的研究对铁路列车追踪问题进行了研究，根据速差和车距运用petri网对列车运行状态及行为进行调整，该研究通过频繁调整后行列车来保证列车的安全性和高效性，但没考虑线路数据对列车追踪的影响，会出现有些情况下高效性无法达到的情况。目前学者对控制器中智能算法的应用及改进关注较多。唐涛等[6]分析总结了一些控制方法在ATO中的应用；随着预测控制的发展，因其实时在线优化调整，具有较好的鲁棒性等优点满足ATO的需求，使预测控制及其改进算法、组合控制在ATO中的应用得到人们的广泛关注；杨辉等[7]采用聚类减法算法得到多个预测模型，提高了控制模型的精确度；衷陆生等[8]采用可变遗忘因子对控制模型进行辨识，提高了预测控制器的抗干扰能力，李中奇等[9]在预测控制的基础上，自适应调节优化时域、控制时域，提高了输出结果对期望曲线的跟踪特性；WANG等[10]针对列车自动驾驶系统中的速度和位移跟踪问题提出迭代学习控制方法，该方法充分利用先前有用的信息来调整当前的操纵策略；SUN等[11]考虑了超速防护的情况，对迭代学习控制方法进行了严格的约束，提高了运行的安全性；LI等[12]在此基础上进一步考虑变参数情况下迭代学习方法，提高了不同工况下列车控制精度，但高精度跟踪效果的实现需要进行足够多次的迭代学习，实时性不好。本文在前人研究探索的基础上对列车追踪进行了研究，提出了追踪动态间隔时间指标，并分析了该指标在列车追踪过程中的变化情况，找到了一种基于列车间实时通信的列车追踪策略。该策略通过保证列车在不利情况下的安全运行，减少在一般情况下的安全余量来缩短追踪间隔时间，实现了追踪列车保持合适的间隔运行，提高了运行效率。

1 列车追踪运行特性

位于同一条线路上，同方向运行的相邻的两列车才考虑列车追踪，因此列车追踪运行是从后车出站信号开放开始，到后车进站时进站信号开放为止。

列车在区间追踪运行时一般情况按运营要求的最高允许速度运行，进入限速区时要进行速度调整，限速值越低，对列车追踪运行影响越大。临时限速服务器规定了CTCS-2级列控系统中限速值分为5档：45，60，80，120和160 km/h。同时查阅了相关规定[13]，发现线路固定限速一般也按此5档设置，因此本文以列车正常运行时会出现的最低限速值为45 km/h研究列车追踪策略。对于事故情况下限速值小于45 km/h时列车追踪运行的情况，本文暂不考虑。

列车间实时通信可以将前车实时的运行信息传送到后车，有利于安全高效运行。目前高铁上采用GSM-R通信的技术比较成熟，并在逐步完善，并且有学者对列车在无地面设施的情况下采用车载设备进行直接通信[14−15]的技术进行了研究。因此本文考虑实现列车间实时通信条件下的列车追踪的策略。

列车追踪间隔时间是列车追踪运行的一项重要指标，该指标在一定程度上体现了列车追踪的安全风险。目前列车追踪间隔时间主要应用于运行图的编制中，为实现处于追踪状态的2列车都按运行图运行，应尽量避免前车对后车的运行造成影响，致使后车偏离运行图运行。通过计算列车发车、区间恒速运行、通过、到站间隔时间，取其中最大值为列车追踪间隔时间。本文将运行图确定的追踪间隔时间称为图定追踪间隔时间Tj。

由于 Tj的分析计算考虑的是列车的整个运行过程[16−17]，是一给定的常数值，而实际情况中，追踪列车进行速度调整时，其追踪间隔时间是在不断变化的，因此现有图定追踪间隔时间指标Tj不适用于列车实时追踪控制，为此本文提出列车追踪动态间隔时间 tj，在速度调整过程中该指标不断变化，是时变指标。最小值为最小追踪动态间隔时间mintj，mintj越小安全风险越大。

式中：sj为列车间动态追踪间隔距离；v为后车实时速度；tj反映追踪间隔时间实时的情况。

2 列车追踪策略分析

列车追踪动态间隔时间tj的变化主要发生在过限速区时速度调整的过程。考虑到一般情况下列车出限速区时，前车先出清限速区，然后尽快加速到最大，恒速运行，后车出清后才开始加速，此过程相当于列车都在按线路数据运行，tj先增大后减小，最终与列车在限速区内运行的追踪间隔时间一致。因此，在列车进限速区时要实现进限速区之前与完全进入后追踪间隔时间一致，否则，出限速区要再进行调整。追踪列车整体减速进限速区时，要考虑安全问题，情况比较复杂，因此针对追踪列车进限速区的情况，本文提出了一种在列车间实时通信满足的条件下可行的方案，与现有列车追踪方案进行对比分析。

根据相关文献[1−3]的分析，在列车按线路数据运行时，本文采用在牵引时以较大的加速度进行牵引，区间按允许速度高速运行，尽量延长牵引—惰行时间的节能策略运行。

方案 1：以图定的追踪间隔时间运行，确保在最不利情况下前车不会影响后车按图运行。

两列车过限速区时，前车先按线路数据减速，后车大致经过一个图定追踪间隔时间 Tj后按线路数据减速。该方案下列车追踪运行情况如图1所示，该方案采用目前列车追踪的思想，表面上列车按一定间隔时间追踪运行，实质是考虑在列车追踪过程中最不利的情况下，给定足够安全的图定追踪间隔时间Tj，保证前车不会影响后车，实现两列车都按线路数据运行。

图1 方案1追踪运行v-t图Fig. 1 V-t chart of train tracking operation according plan 1

图1 为从前车开始减速的时刻开始，两列车速度随时间的变化情况，v1为本分区最高允许速度；v2为限速区最高允许速度；t1是列车以常用制动ac从v1减到v2用的时间；前车减速完后经过t2后车开始减速(t2=Tj−t1)。整个减速过程，后车速度(实线)一直高于前车速度(虚线)，两车间的距离一直在缩小，2条线围成的面积为整体减速前后两列车追踪间隔距离的变化量Δs。

优点：该方案可以实现调速前后追踪间隔时间一致，追踪过程中列车始终按线路数据运行，保证追踪运行的两列车按运行图运行。

缺点：列车按该方案追踪运行时，图定追踪间隔时间 Tj到最小追踪间隔时间的 mintj的变化量较大，mintj越小，列车追踪运行的安全风险越大。

该方案下追踪列车减速过程中，在t1和t2阶段，后车速度不变，追踪间隔距离在快速减小，t2阶段结束后后车速度才迅速减小，整个过程相当于先把距离减小再去减小速度，导致该方案下tj的变化率和变化量都较大，即Tj到 mintj的变化量较大，当mintj固定时Tj的取值较大。

为减小追踪列车减速调整时Tj到mintj的变化量本文提出方案2。

3 方案2分析与确定

方案 2：调整前后车，让后车滞后前车一定时间t0后，以目标点为限速区起点减速度为a0开始减速。t0，a0的取值需要分析它们与mintj关系确定，该方案具体参数取值要根据实际运行数据确定。

3.1 方案2追踪过程分析

经过理论分析可知，采用方案2后，列车追踪运行情况如图2所示。

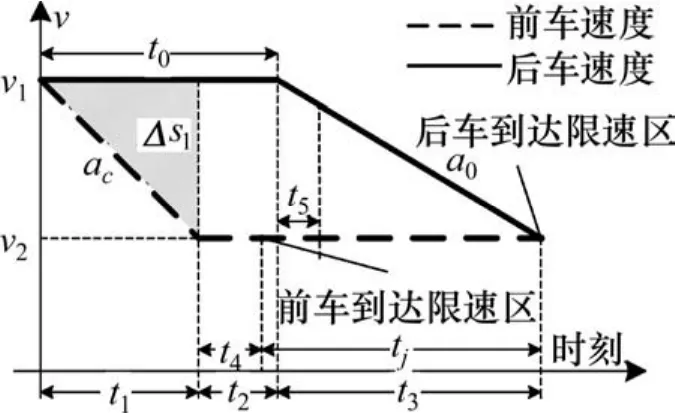
图2 方案2追踪运行v-t图Fig. 2 V-t chart of train tracking operation according plan 2

图2 中：v1，v2，t1，t2，Δs和ac与图1含义相同；Δs1为t1时间内两车间隔距离的变化量；t3是后车以a0由从v1减到v2用的时间；t0为后车滞后前车减速的时间。由图可知追踪列车整体减速过程分为t1，t2和 t33 个阶段，此时 0≤t2≤Tj−t1。

为保证列车进入限速区前后追踪间隔时间一致，必须满足进入限速区前后间隔距离变化量Δs=Δv·Tj，要保持Δs不变，即四边形面积不变，当后车滞后前车t0时间减速时，由于四边形上边由Tj减到t0，因此下边应适当增加一段时间t4，即将限速区起点位置向列车所在的区间移了一段距离。

本文通过v-t图分析了该方案下tj的变化过程，由此确定mintj与各参数关系。由四边形面积公式求该方案下Δs。

由：

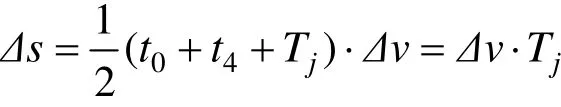
得：

由于t1的值相对较小，假设t0大于t1，由图2可知：

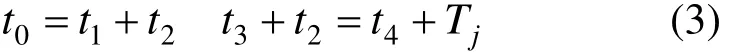
后车采用与前车不同的减速度a0，由于a0的取值与目前列车各制动等级对应减速度不同，因此需要对列车自动驾驶技术做进一步研究，实现列车按期望曲线运行。结合式(2)和(3)得a0计算公式如下：

当 Δv确定后t1就确定，列车滞后减速时间t0可用t2代换，分析 mintj随 t2变化情况。mintj可能在t2阶段结束时取到，也可能在t3阶段取到，因此要分情况考虑。

情况1：mintj在t2结束取到，其计算公式如下：

式中：s1=v1·Tj，是前车开始减速前两车间隔距离。

情况2：mintj在t3阶段运行t5时间后取到，在t3阶段时tj的计算如下：

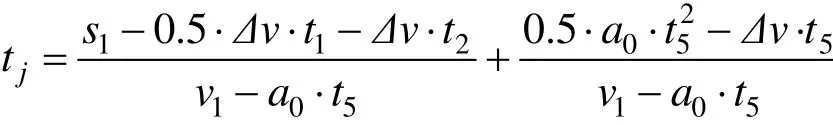
对tj求一阶导得：

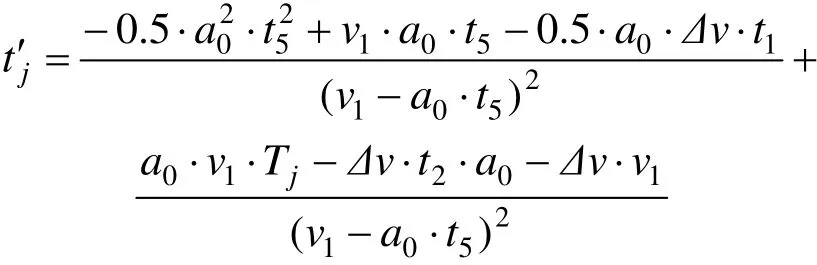
令 tj一阶导为 0，可求得 tj取得极小值时 t5的值：

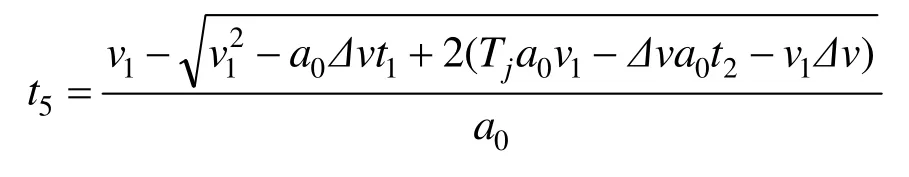
若计算得t5大于0则mintj可在t3阶段取得，否则要按情况1计算。

将求得的t5带入tj计算式得到极小值，即mintj。该值与 v1，Δv，Tj，a0，t2，t1均有关，其中 v1，Tj，Δv可通过线路信息获得，通过实时通信可获得前车信息ac，结合线路信息可确定t1取值。当v1，Δv，Tj，t1确定后，a0只与 t2有关，因此 mintj仅随 t2变化。

3.2 增大mintj的措施

Tj相同时，mintj越大说明对应方案安全风险越小。当各参数给定值不同时，mintj随t2变化的曲线不同。考虑到 t3阶段 mintj计算公式较为复杂，本文运用 matlab仿真得到 Tj，Δv为几种不同给定值时mintj随t2变化的曲线，计算结果如图3所示。2种情况下变化曲线相切，t2取值大于切点对应时间时，t5小于 0，实际按情况 1变化，否则按情况 2变化。

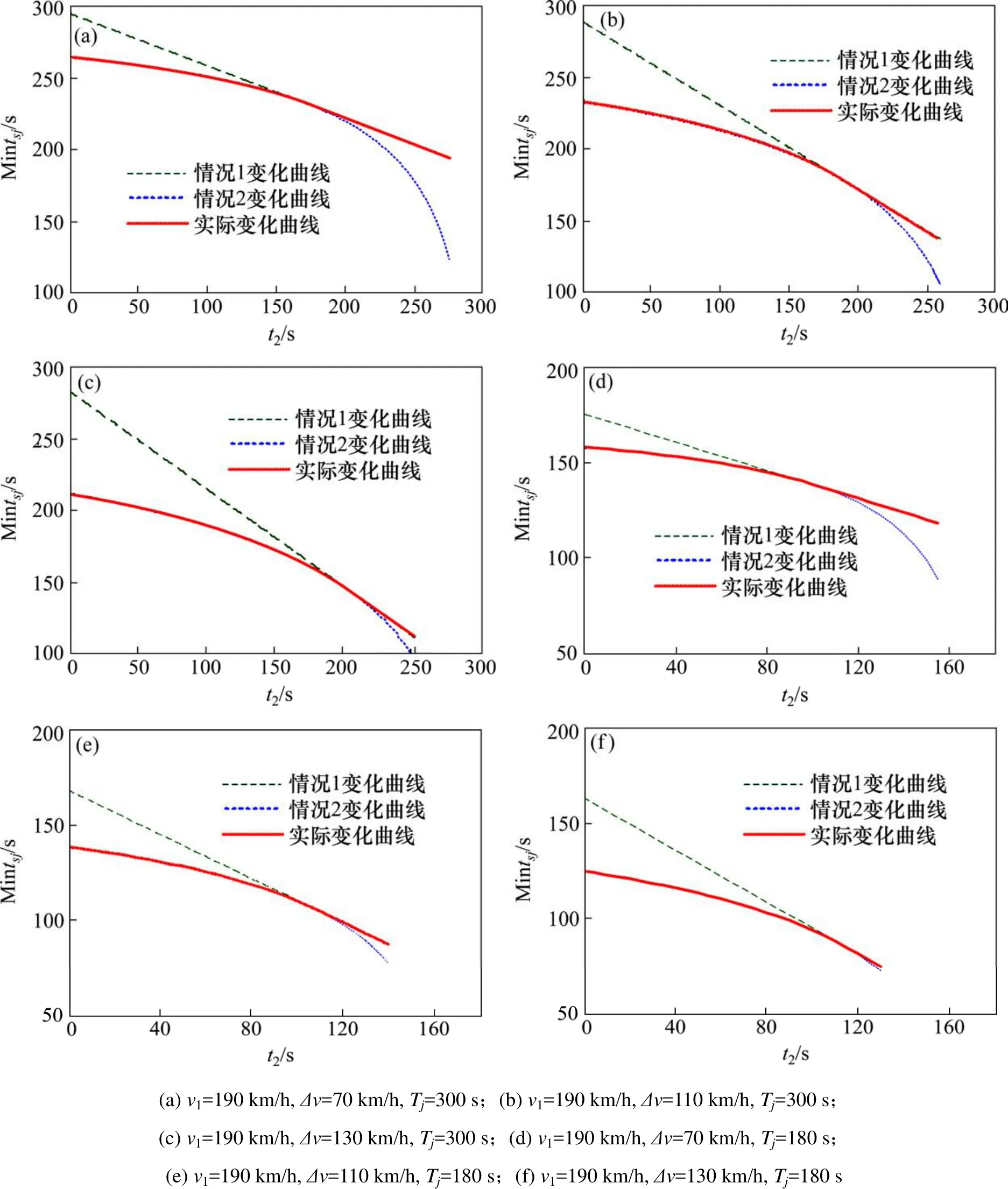
图3 不同情况下mintj随t2变化的曲线Fig. 3 Curves of mintj change with t2 in different condition

由单个图中曲线变化情况可知，随 t2的减小mintj逐渐增大；通过纵向对比可以发现 mintj随Tj的减小而整体减小；通过横向对比可以发现 Δv越大，即情况越不利时，mintj的变化率越大。由此可以得出增大mintj，减小追踪安全风险的措施：1)减小t2；2)增大Tj；3)尽量避免Δv过大的情况。

3.3 滞后时间t0取值分析

列车追踪运行必须满足最不利情况下的安全要求，而该情况下Δv较大，mintj的整体变化率较大，减小 t2对增大 mintj效果明显，而在 t2接近 0时变化率逐渐减小，对增大mintj的效果降低，因此t2取值应再0~60 s之间适当选取。t2确定后可由式(2)和(3)求得 t0。

3.4 方案2运行效率的分析

当t2取值较小时，列车追踪运行的安全风险有了较大改善，但前车减速完成后经过t4才能到达限速区，致使整体进入限速区的时间比方案1长，效率会有所下降。为此本文在保证安全的前提下适当减小Tj，提高效率。Tj确定后，结合实际，综合考虑可确定t2取值，本文实例中t2取值为20 s。

方案2最终策略为：前车提前减速，减速完成后经过t4到达限速区，前车开始减速一段时间t0后，后车开始减速，以限速区起点为目标点a0为减速度减速，在保证列车运行安全的前提下适当减小Tj，保证整体的运行效率。

由于实际情况中的 Tj是在保证安全的前提下适当选取，并留有一定余量保证准点性。因此确定方案2取值时应先取t2最小值为0时，分析Tj不同时该方案下mintj，并与方案1对比确定Tj，在充分保证安全运行的同时Tj取值应尽量小，缩短发车间隔；然后再分析 t2不同时 mintj的值，适当增大t2(0~60 s)，牺牲部分安全余量来缩短整体调整时间，当 t2和 Tj确定时，结合式(2)，(3)和(4)可求得a0，t4和t0的值。

4 各方案对比及仿真分析

为分析方案2在实际情况中的是否可行，本文结合实际，理论分析了各方案追踪效果。本文以200 km/h为线路最高限速，考虑各等级防护曲线与测速误差的影响，设计列车以 190 km/h运行，限速为45 km/h时列车按40 km/h运行，追踪过程中最不利情况为190~40 km/h调速阶段；取紧急制动为1.12 m/s2，常用制动ac为0.78 m/s2，对该过程方案1与方案2的追踪情况进行对比分析。

由mintj随t2变化曲线图可知，采用方案1时，即 t2取最大值时，mintj在 t2阶段取得，将 t2=Tj−t1代入式(5)，即可求得采用方案1时mintj的值；当t2取20 s时，mintj在t3阶段取得，由上述分析计算可得方案2时mintj。对同条件下方案1与方案2的计算结果进行对比分析。结果如表1所示：

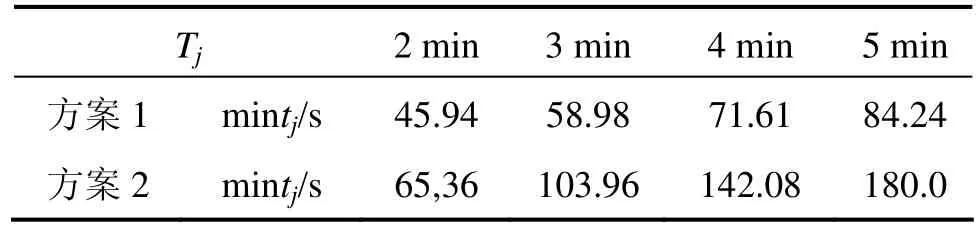
表1 190~40 km/h追踪过程中mintjTable 1 Mintj of trains tracking operation from 190 km/h to 40 km/h

文献[16]和[17]中分析给出允许速度为 200 km/h时，3 min追踪间隔时间可以满足列车发车、区间恒速运行、通过、到站追踪时的需求，但没考虑追踪列车减速进限速区追踪间隔时间实时变化的情况，本文对此进行了考虑，得出方案1按3 min追踪时，在该情况下追踪间隔会缩短为58.98 s，安全风险比方案2大。

而目前实际情况中，列车采用方案1按5 min追踪运行，由表中分析结果可知，方案2按3 min追踪时计算得到的mintj大于方案1按5 min追踪时求得的值，即采用方案2按3 min追踪的策略可以保障追踪列车安全运行。

方案2与方案1比较整体速度调整所需时间的差值Δt计算公式如下：

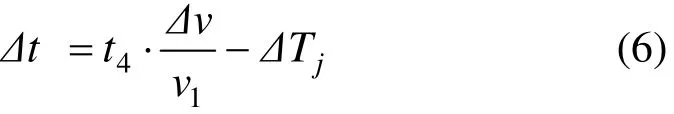
式中：ΔTj为方案2与方案1相比图定追踪间隔时间Tj的减小量，若Δt为正值，则方案2整体通过时间比方案1大，效率较差，反之则好。

若采用方案2按5 min追踪运行时，整体通过时间变化量由式(6)求得：

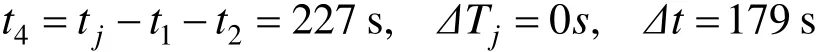
整体过限速的时间明显增大，影响列车运行效率。若按3 min追踪运行时其整体通过时间由式(6)求得为：

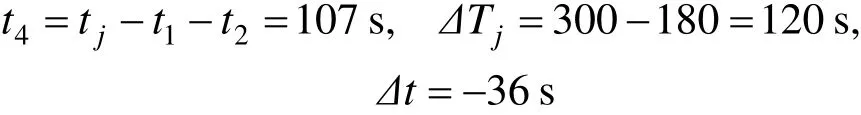
由计算结果可知，t2取20 s时，该方案在不利情况下对整体通过限速的时间缩短，效率好于方案1。当t2取值不同时，方案2按3 min追踪运行的mintj与效率会逐渐变化，其计算结果如表2所示。

由于本文对列车运行方案的计算与研究都是采用期望曲线进行理论分析的，因此通过控制器保证列车较好的跟踪期望曲线十分必要，为此本文设计了模糊预测分层控制器，控制列车按方案2追踪运行。

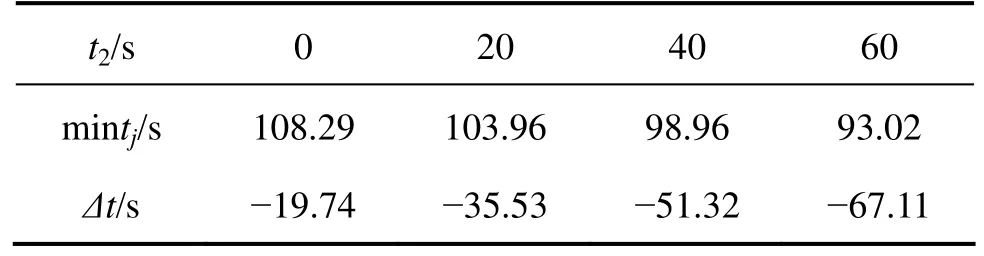
表2 方案2 3 min追踪t2取值不同时运行结果Table 2 Different results of trains tracking operation according plan 2 when Tj is 3 min

本文通过 matlab对各方案追踪运行进行了仿真分析。采用2列CRH2A重联列车过同一段限速区，分别以方案1按5 min追踪和以方案2按3 min追踪，考虑最不利追踪情况，线路限速为 200~45 km/h，列车允许速度为190~40 km/h。

仿真结果如图4~9所示。

表3 CRH2A列车相关数据Table 3 Train date of CRH2A

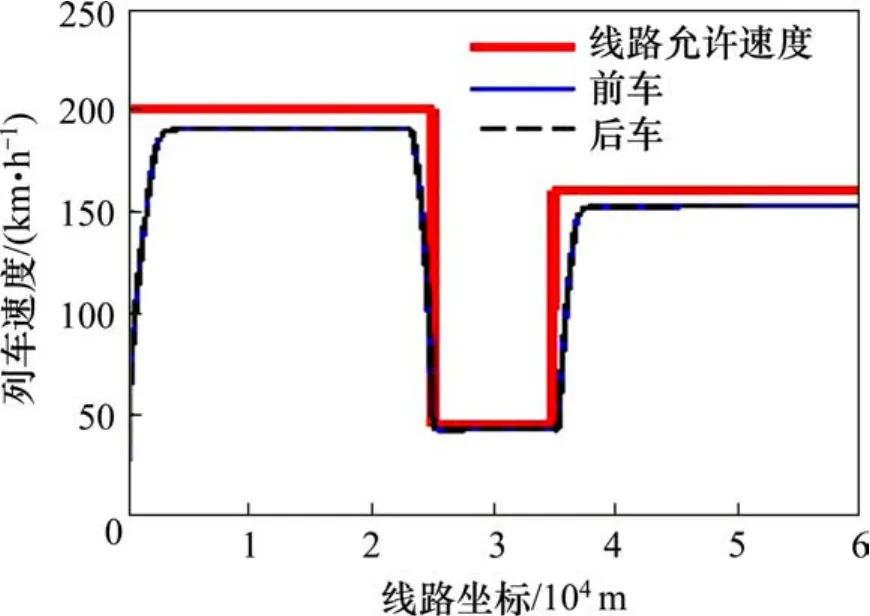
图4 方案1追踪运行v-s图Fig. 4 V-s chart of train tracking operation according plan 1

由仿真图可以看出，从前车发车到后车达到限速恒速运行的过程，前车速度一直高于后车，2车间间隔距离不断增大，而后车速度很低，tj由无穷大逐渐减小，2列车恒速追踪时 tj不在变化，此时tj与Tj相等，出限速时与此情况相同，进限速时按各追踪方案运行。

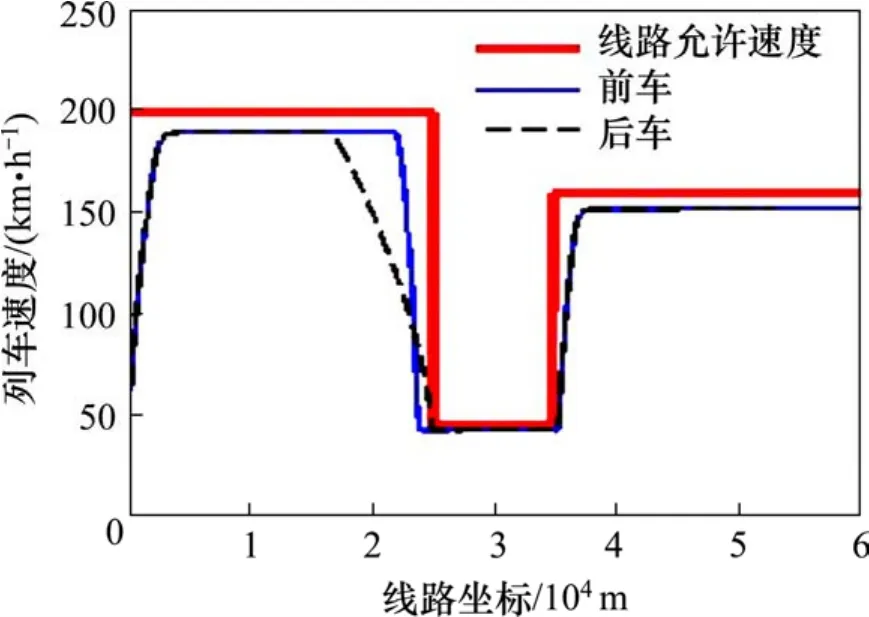
图5 方案2追踪运行v-s图Fig. 5 V-s chart of train tracking operation according plan 2

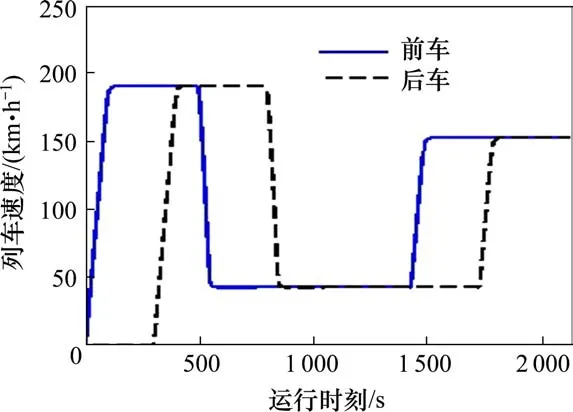
图6 方案1追踪运行v-t图Fig. 6 V-t chart of train tracking operation according plan 1

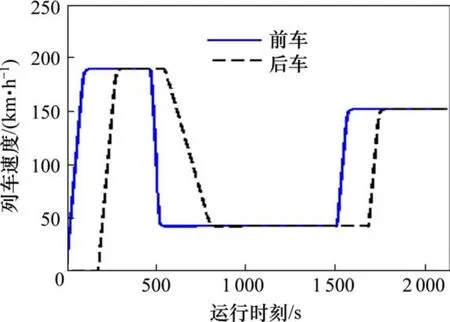
图7 方案2追踪运行v-t图Fig. 7 V-t chart of train tracking operation according plan 2

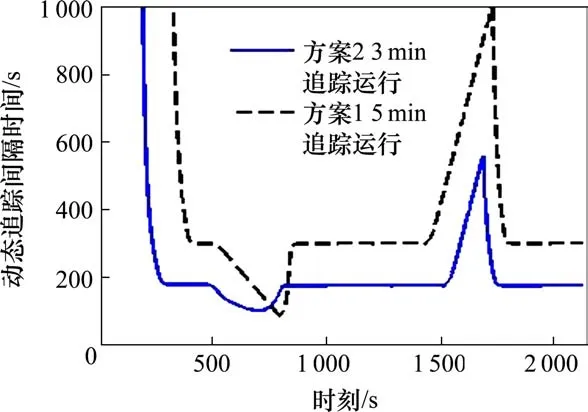
图8 动态追踪间隔距离变化情况Fig. 8 Situation of dynamic tracking distance change with time

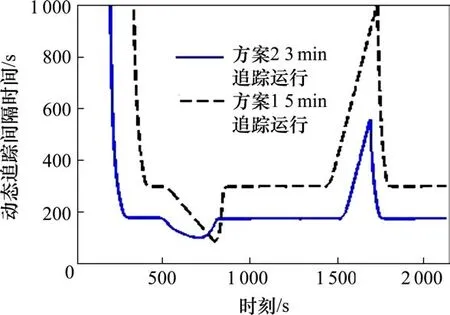
图9 追踪运行tj-t图Fig. 9 tj-t chart of train tracking operation

方案1按5 min追踪运行是目前普遍采用的追踪方案，由各方案仿真对比可以看出，列车采用方案2按3 min追踪运行可以达到采用方案1按5min追踪运行的效果，安全风险较低，整体通过效率较好，与理论分析结果一致。因此方案2按3 min追踪适用整个追踪过程。

5 结论

1) 通过引入列车追踪动态间隔时间指标tj，并以该指标分析列车追踪过程中追踪间隔时间实时变化情况，得出在追踪列车减速调整过程中改变追踪策略，实现在列车间距减小的同时减小后车速度可以有效增大最小追踪间隔时间，明显减小列车追踪的安全风险。

2) 为实现追踪列车减速调整过程中在列车间距减小的同时减小后车速度，结合铁路相关运营要求，本文提出了方案2列车追踪策略，可以在保证追踪安全的前提下缩小图定追踪间隔时间，从而提高行车密度，提高运营效率。

参考文献：

[1] William C C, Asunción P C, Antonio Fernández-Cardador.Fuzzy train tracking algorithm for the energy efficient operation of CBTC equipped metro lines[J]. Engineering Applications of Artificial Intelligence, 2016(53): 19−31.

[2] 林颖, 王长林. 车载 ATO运行等级模式曲线的计算模型研究[J]. 铁道学报, 2013, 35(7): 50−56.LING Ying, WANG Changlin. Computational model of operation level type profile of onboard ATO[J]. Journal of the China Railway Society, 2013, 35(7): 50−56.

[3] GU Qing, TANG Tao, MA Fei. Energy-efficient train tracking operation based on multiple optimization models[J]. Intelligent Transportation Systems, 2016, 17(3): 882−892.

[4] 王鹏玲, 王青元, 崔恒斌, 等. 考虑列车追踪的自动驾驶控制算法[J]. 西南交通大学学报, 2013, 48(6): 1045−1051.WANG Pengling, WANG Qingyuan, CUI Henbin, et al.Automatic train control algorithm for train tracking[J].Journal of Southwest Jiaotong University, 2013, 48(6):1045−1051.

[5] 潘登, 郑应平. 高速列车追踪运行的控制机理研究[J].铁道学报, 2013, 35(3): 53−61.PAN Deng, ZHENG Yingping. Study on the mechanism of high-speed train following operation control[J].Journal of the China Railway Society, 2013, 35(3): 53−61.

[6] 唐涛, 黄良骥. 列车自动驾驶系统控制算法综述[J].铁道学报, 2003, 25(2): 98−102.TANG Tao, HUANG Liangji. A survey of control algorithm for automatic train operation[J]. Journal of the China Railway Society, 2003, 25(2): 98−102.

[7] 杨辉, 张坤鹏, 王昕, 等. 高速列车多模型广义预测控制方法[J]. 铁道学报, 2011, 33(8): 81−87.YANG Hui, ZHANG Kunpeng, WANG Xin, et al.Generalized multiple-model predictive control method of high-speed train[J]. Journal of the China Railway Society,2011, 33(8): 81−87.

[8] 衷陆生, 颜真, 龚锦红, 等. 时变遗忘因子的高速列车自适应子空间预测控制[J]. 铁道学报, 2013, 35(3):54−61.ZHONG Lusheng, YAN Zhen, GONG Jinhong, et al.Adaptive subspace predictive control of high-speed train based on time-varying forgetting factors[J]. Journal of the China Railway Society, 2013, 35(3): 54−61.

[9] 李中奇, 杨振村, 杨辉, 等. 高速列车双自适应广义预测控制方法[J]. 中国铁道科学, 2015, 36(6): 120−127.LI Zhongqi, YANG Zhencun, YANG Hui, et al.Generalized predictive control with dual adaptation method of high-speed train[J]. China Railway Science,2015, 36(6): 120−127.

[10] WANG Yi, HOU Zhongsheng, LI Xingyi. A novel automatic train operation algorithm based on iterative learning control theory[C]// Proc1 IEEE Conf1Service Operations, Logis-tics and Informatics, 2008: 1766−17701.

[11] SUN Heqing, HOU Zhongsheng, LI Dayou. Coordinated iterative learning control schemes for train trajectory tracking with overspeed protection[J]. Automation Science and Engineering, 2013, 10(2): 323−333.

[12] LI Zhenxuan, HOU Zhongsheng, YIN Chenkun. Iterative learning control for train trajectory tracking under speed constrains with iteration-varying parameter[J].Transactions of the Institute of Measurement and Control,2015, 37(4): 495−493.

[13] 中国铁路总公司. 铁路技术管理规程[S].China Railway Corporation. Train traffic regulations[S].

[14] 陈启香, 李茂青, 林俊亭. 基于超短波的列车间直接通信技术的研[J]. 计算机工程, 2013, 39(12): 5−10.CHEN Qixiang, LI Maoqing, LIN Junting. Research on train-to-train direct communication technology based on ultrashort wave[J]. Computer Engineering, 2013, 39(12):5−10.

[15] 李淑娟, 李茂青, 高云波, 等. 列车间多频段直接通信系统设计及性能分析[J/OL]. 计算机工程与应用, 2017,53(13): 104−112.LI Shujuan, LI Maoqing, GAO Yunbo, et al. Performance analysis of multiband direct communication between trains in tunnel[J]. Computer Engineering and Applications, 2017, 53(13): 104−112.

[16] 田长海, 张守帅, 张岳松, 等. 高速铁路列车追踪间隔时间研究[J]. 铁道学报, 2015, 37(10): 1−6.TIAN Changhai, ZHANG Shoushuai, ZHANG Yuesong,et al. Study on the train headway on automatic block sections of high speed railway[J]. Journal of the China Railway Society, 2015, 37(10): 1−6.

[17] 韩兰奎, 李茂青, 董昱, 等. 列车编队运行方式研究[J].兰州交通大学学报, 2015, 34(3): 66−74.HAN Lankui, LI Maoqing, DONG Yu, et al. Research on the formation mode of train operation[J]. Journal of Lanzhou Jiaotong University, 2015, 34(3): 66−74.