链码跟踪在矩形检测中的应用∗

袁铸 张毅

（河南工业职业技术学院 南阳 473000）

1 引言

几何图形的识别是计算机视觉领域的重要任务之一，它主要应用于设计自动化、深海探测及国防建设等。就矩形检测问题而言，国内外学者对矩形检测研究做了不少工作并取得了不少实际应用，如低温电子显微镜图像中提取矩形状的棵粒物，图像和视频中的车牌提取，建筑知识图和布局设计知识图求解，卫星图片建筑物提取，公路监视系统车牌检测。迄今为止，已提出了许多矩形检测方法，可主要分为如下几类：

1）基于Hough变换及其改进的算法：标准Hough变换最初使用于直线检测，因其具有良好的抗噪性，现已广泛运用于具有线性特征的物体检测。矩形是具有优良几何性质的线性图形，其每条边均可用Hough变换检测出。但因Hough变换检测直线时，丢失了直线端点信息，为恢复直线的端点无疑要增加算法的计算复杂度，故一些学者对Hough变换进行改进以适用于矩形检测。Zhu［1］等研究出检测矩形的Hough变换用于在低温电子显微镜图像中检测近似矩形的尘埃粒子的检测，该方法通过采样估计出近似矩形的尘埃粒子的长和宽后，先利用图像边缘局部信息和2-D累加器检测出矩形的中心坐标，再用一个1-D累加器检测出矩形的方向。该方法检测速度快，但精度过低。Claudio等［2］提出了窗口化的Hough变换矩形检测方法，该方法将矩形四条边进行Hough变换后参数空间对应峰值点的性质确定侯选矩形中心坐标（x0，y0），然后对以该中心为圆心，包含该侯选矩形最小圆和不与该侯选矩形相交的最大圆组成的圆环区域进行Hough变换以确定侯选矩形的长a，宽b和方向角3个参数。该方法的优点是抗噪声能力强，图像边缘可以不连续；缺点是由于采用的是STH，故有较大的计算量。

2）基于直线组合的方法：因矩形是由互相垂直的两组平行直线组成。一些学者提出可利用直线检测的结果判断图象中是否存在矩形并确定其参数。Lagunovsky［3］等提出一种基于直线基元检测的矩形检测方法。该方法首先从图像中检测所有直线并且在已检测的每条直线中找出线段；接着通过比较线段的长度和方向确定出四边形并按矩形的定义确认出真矩形。Lin［4］等研究出基于直线检测的矩形检测算法，用于航空拍摄的建筑图像检测问题。其思路是在直线检测时找出某一长度范围的线段，对每一条线段，搜索出与之垂直的线段并检测出对应的矩形。Tao［5～7］等使用分裂算法提取被检测图像中的边缘线段。利用线段的基本信息（起点、终点坐标和斜率）找出并行线段组。将并行线组构成矩形基元后合并成矩形。这些方法的检测效率一方面直接依赖于检测直线的效率，另一方面在图像中若矩形的个数很多时，还产生大量的无效线段组合，检测效率将进一步降低。

作者研究的是复杂布局设计中图形的检测。如图1（a）所示的卫星舱布局求解问题［8～9］的二维问题，可归结为在一个圆容器中布置若干圆形、矩形待布物的带性能约束（如动力约束）复杂布局设计问题（如图1（b）所示），而对图像空间的多个矩形的检测是该布局设计中待解决的问题之一。对于前两类方法检测矩形，显然，第一类方法由于采用的是标准Hough变换的投票机制，故必须花费较多的检测时间。第二类方法的检测效率和检测精度依赖于直线检测算法和直线数目。因此，它们难以实现复杂布局图形的多矩形检测。

图1 卫星舱的布局图及平面布局图

对于边缘连续的矩形检测问题，如果能找出每一个候选矩形的链码，就能快速找出该候选矩形的四个顶点，根据矩形的定义就能快速确认出该候选矩形是否是真矩形。根据这一思想，文献［10］提出基于广义Hough变换的快速多矩形检测方法。但它只能检测不相交的多个矩形，对于相交或被遮挡的情形仍然有待研究。为解决该问题，本文提出了一种可较好地应用于相交矩形的检测算法。实验结果表明，该算法有检测精度高、速度快的优点，能较好地应用于复杂布局设计中矩形检测。

2 相关定义及理论

本文中所处理的图像均为二值化图像，如果图像中不为二值图可通过阈值变换将其转换为二值图像。关于图像点、非图像点、孤立噪声点、半连续噪声点的定义请参考文献［11］。

设矩阵A=［aij］H×W表示图像空间的0，1数字化信息（图像点值为1，非图像点值为0）。其中W为图像空间的宽度，H为高度，i为图像中象素的y坐标值，j为x坐标值。

定义1 设在直角坐标系中，矩形的左下角顶点坐标为（x1，y1），右下角顶点坐标为（x2，y2），右上角顶点坐标为（x3，y3），左上角顶点坐标为（x4，y4），则该矩形记为R（x1，y1，x2，y2，x3，y3，x4，y4）。

两平行矩形相交有以下几种可能：1）一矩形分裂成两新的小矩形。如图2（a）所示，矩形R1、R2相交后演变为三矩形 R1、R21、R22。2）产生一新的矩形。如图2（b）所示，矩形R1、R2相交后演变为三矩形 R1、R2、R12。3）其中一矩形的一边被遮挡而无法求解该矩形。如图2（c）所示，矩形R1、R2相交后演变为矩形R1。为避免前两种情形发生，且能较好地符合视觉习惯，本文规定所求解矩形需符合规则1：

图2 两平行的矩形相交

规则1 数字图像中直线段最多只能属于一个矩形，且优先属于大矩形。

定理1 在数字图像中，设其最短连续曲线长为l，则图像点P是连续曲线上的点的必要条件是以P为中心、边长为2r+1的正方形区域中图像点个数不小于 r+1（r+1＜l）。

证明：反证法。假设P是连续曲线上一点，以P为中心的边长为2r+1的正方形区域中图像点个数NP＜r+1。由最短连续曲线长为l可知，若P是连续曲线上一点，则在以P为中心、边长为2l+1的正方形区域中至少存在一图像点个数不小于l的连通图像点区域；由连续曲线的生成算法可知，在以P为中心、边长为2r+1的正方形区域中至少存在r+1个图像点（r+1＜l）。故NP ≥ l＞r成立，这与假设中NP＜r+1矛盾，因此假设不成立，定理得证。

证毕

定义2 数字图像中孤立和半连续噪声点及不满足定理1的图像点称为第一类非曲线噪声点；除第一类非曲线噪声点外的不在曲线上的图像点称为第二类非曲线噪声点。

由定理1知，不满足定理1的图像点必不在连续曲线上。故在检测前，可剔除第一类非曲线噪声点来提高图像质量以利于检测。图3（b）为剔除图像中第一类非曲线噪声点后的效果图（其中l=5），可以看到经此处理后绝大部分噪声点被剔除。

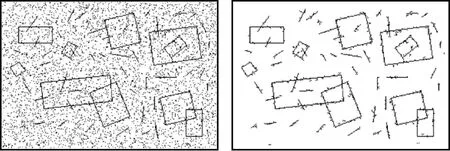
图3 预处理效果图

3 算法思想

3.1 数据结构

3.2 不相交封闭图形的链码跟踪思想

设当前点为P（x，y），将其8个邻接点按图4所示进行编码，可通过如下步骤实现对不相交封闭图形的链码跟踪：

1）从左到右、从下到上地搜索。将第一个图像点作为图形的起点Ps，并将其记为当前点PCur，搜索下一个图像点。

2）搜索当前点PCur的八邻域中未跟踪过的图像点数NP，将当前点PCur信息（followLink-＞node⁃Num，followLink-＞x，followLink-＞y，followLink-＞neighborsNum）插入到跟踪链表中，并将当前点PCur标记为已跟踪，再根据NP来选择下一跟踪点：若NP=1，直接将该图像点作为下一跟踪点PNext；若NP＞1，从图4所示的链码方向中优先选择链码方向值小的图像点作为下一跟踪点PNext；若NP=0，则回退到跟踪链表中的前一NP＞1的结点处（即followLink-＞NeighborsNum＞1）。并将PCur其设置为PNext。

图4 链码方向

3）重复第二步直至|PsPCur|＜wd（wd为不封闭的阈值），若跟踪链表中结点个数（即followLink-＞nodeNum）大于最小图形周长阈值Lw，则跟踪结果为封闭图形；否则，跟踪结果不为封闭图形，清空跟踪链表来跟踪下一个封闭图形。

3.3 相交矩形的轮廓跟踪

3.2节所述的轮廓跟踪方法可适用于不相交图形的跟踪，但难以适用于相交图形（如图5（b）所示）。根据矩形的几何性质，本文将轮廓跟踪法加以了改进以适用于矩形跟踪：

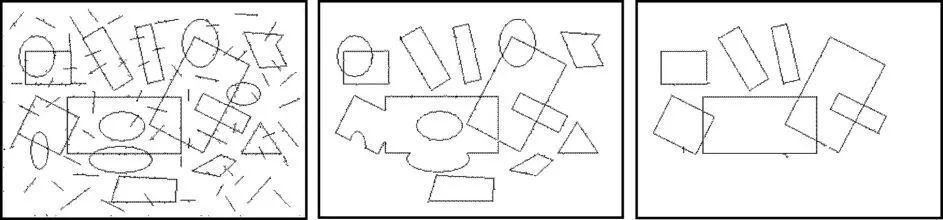
图5 轮廓跟踪效果对比

1）在跟踪过程中将跟踪点存入到局部跟踪点集合SegmentSet中，并计算这段拟和直线段的角度。根据拟和直线的角度差可排除直线和相交矩形的干扰。

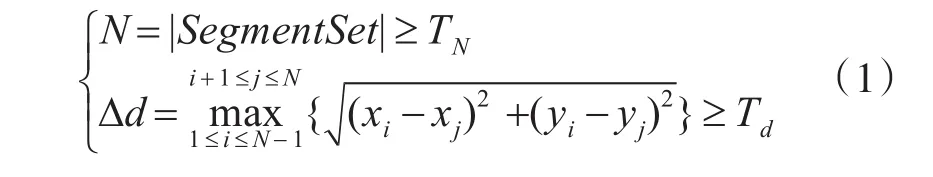
在跟踪过程中将当前点存到集合SegmentSet中，若集合SegmentSet不满足式（1），则继续下一图像点的跟踪；否则，对其用最小二乘法作拟和直线l：ay+bx+c=0，其中直线参数可由式（2）求出。

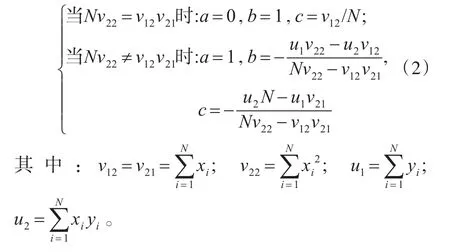
求得拟和直线参数后，可由式（3）求得该拟和直线的倾斜角度θk。

再利用SegmentSet中起点（x1，y1）和终点（xN，yN）信息，由式（4）求得该拟和直线段的角度θt，将θt及SegmentSet中点的坐标存入拟和直线段链表angleLink，再将集合SegmentSet清空。

其中：情形1：θk＞0&&xN ≥ x1&&yN ≥ y1；情形2：θk＞0&&xN ≤ x1&&yN ≤ y1；情形 3：θk＜0&&xN ≤x1&&yN ≥ y1；情形 4：θk＜0&&xN ≥ x1&&yN ≤ y1；情形5：θk=0，xN＞x1；情形6：θk=0，xN＜x1。

在求得当前拟和直线段的角度θtn后，根据式（5）计算该拟和直线段的角度与前n-1段拟和直线段（θt1，θt1…）的夹角和 sumθtn和夹角平均值aveθtn。

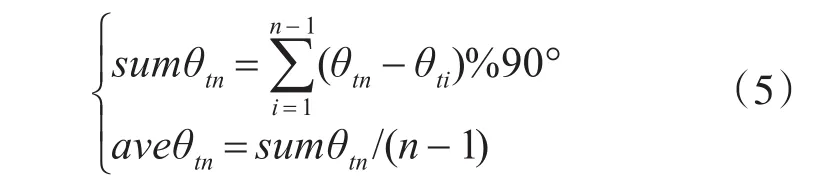
设定阈值 Tw ，若 aveθtn＜Tw ，置angleLink-＞flag为0。若 aveθtn≥Tw ，置angleLink-＞flag为1；若aveθtn连续两次大于Tw，将拟和直线段链表an⁃gleLinks上对应于这两段拟和直线段的结点的flag置为2，并回退至跟踪链表followLink中上一neigh⁃borsNum＞1的结点处。如此，可排除大部分直线段和相交矩形（倾斜角相差较大）的干扰。

2）在多岔口处优先跟踪拟和直线段方向以加快检测速度。

若当前点存在多个后继点时，需从中选择一点来作为下一跟踪点。本文利用当前点的前一拟和直线段的角度θ来确定主方向和次方向，并优先考虑主方向和次方向。在主方向和次方向上都不存在图像点时，按图4所示的链码方向从小到大来选择图像点作为下一跟踪点。其中，主方向为方向序号为偶数（0，2，4，6）且与 θ 最为靠近的方向，次方向为方向序号为奇数（1，3，5，7）且与θ最为靠近的方向。

3）如果当前点八邻域中没有未跟踪的图像点，则在以该点为中心，长为2Lw+1的正方形区域D中搜索未跟踪的图像点作为下一跟踪点。如果D中仍无未跟踪的图像点，则回退到跟踪链表中上一neighborsNum＞1的结点处。

3.4 矩形顶点计算及真矩形确认

通过以上算法可跟踪得到图像中近似于矩形的图形（如图5（c）），称其为候选矩形。

将拟和直线段li按式（6）分为四类：

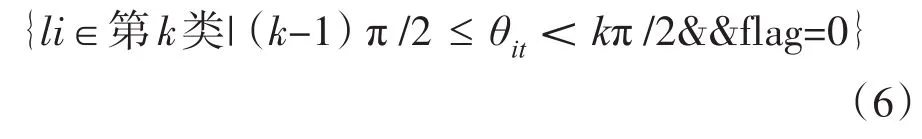
分类后，第k类拟和直线段在候选矩形的第k边。将第k类拟和直线段上所有点用最小二乘法求解所得的拟和直线方程，即为矩形第k边的直线方程lrk：aky+bkx+ck=0。将矩形两邻边的直线方程联立得式（7）：

其中，n=（m+1）%4（m=0，1，2，3）。

由式（8）可求解得候选矩形两邻边的交点，即候选矩形的顶点（xm，ym）：

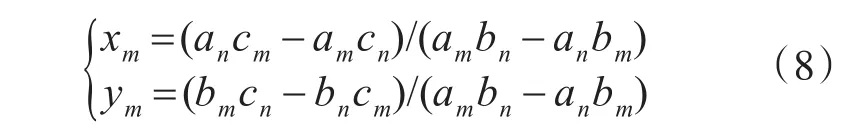
计算得候选矩形顶点P0（x0，y0），P1（x1，y1），P2（x2，y2），P3（x3，y3）后，若落在候选矩形R（x0，y0，x1，y1，x2，y2，x3，y3）各边上的点数 Mic（i=0，1，2，3）均大于该边长度的w倍（w为比例系数，w＜1&&w＞0），则为真矩形；否则，为虚假矩形。

4 数值实验与讨论

以下实验是在4GB内存的双核i3 3.4 GHz计算机上用VC++6.0编程实现的。在待检测图中，坐标原点规定为矩形左下角，坐标轴分别平行于矩形的两相邻边。在本文中，将文献［5］中算法称为Tao算法。

实验1 图形检测实例

为验证、对比算法的检测性能，做了如下两组实验：1）只含噪声点干扰；2）含噪声点和线条干扰。

图6（a）为含7个矩形、6个椭圆、4个多边形的331×234的图像空间。在第一组实验中，我们对图6（a）增加不同程度的噪声点，噪声点个数为图像空间像素点个数的1%～10%（如图6（b）所示）。在第二组实验中，我们对图6（a）增加干扰线条和噪声点，干扰线条条数为0～60，噪声点个数为图像空间像素点个数的0%～3%（如图6（c）所示）。

图6 多种图形中矩形检测实例

本文算法对6（a），6（b），6（c）检测结果基本相同且与精确值相差不超过两个像素（如表1所示），如图6（d）所示为对6（a），6（b），6（c）的检测效果最差的图。

表1 本文算法对图6（b）的检测结果

表2为第一组实验中，Tao算法和本文算法的检测性能对比。其中，对图6（b），Tao算法的平均检测时间为0.09s，本文算法的平均检测时间为1.36s。

表3为第二组实验中，Tao算法和本文算法的检测性能对比。其中，对图6（c），Tao算法的平均检测时间为0.11s，本文算法的平均检测时间为1.33s。

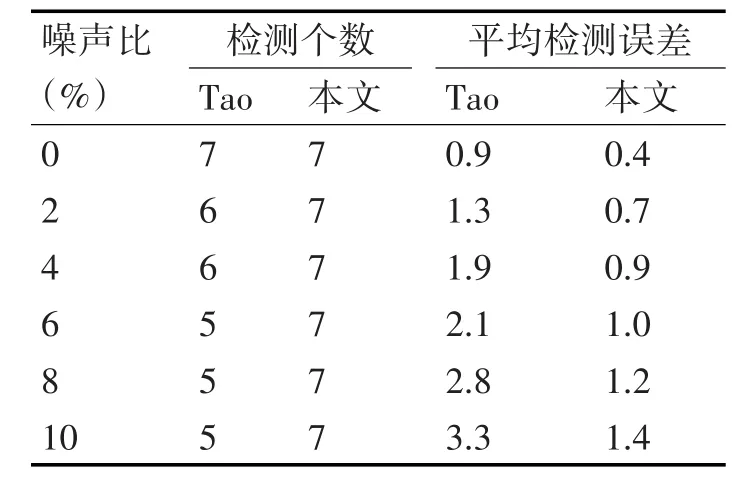
表2 实验1中第一组实验的算法检测性能对比表

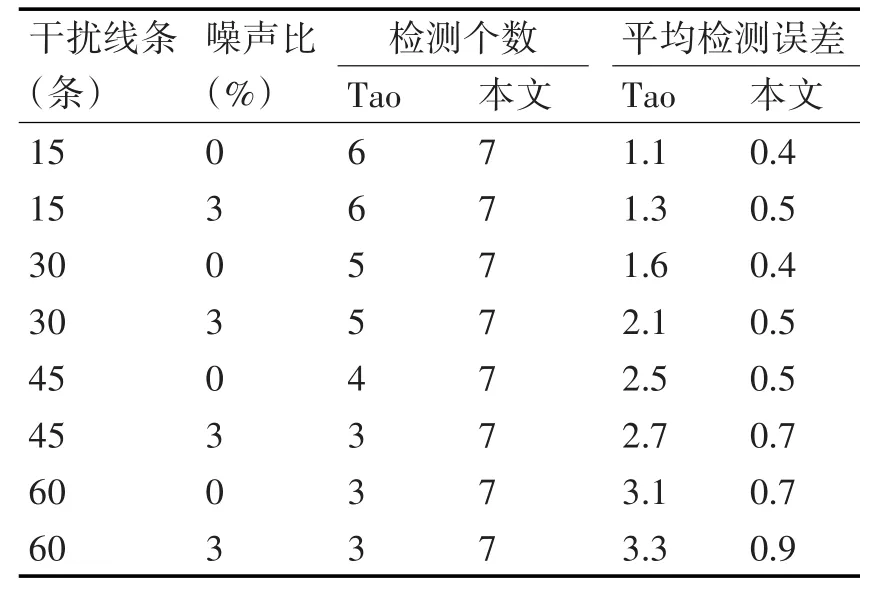
表3 实验1中第二组实验的算法检测性能对比表

虽然Tao算法的检测速度要比本文算法快，但该算法的检测精度要低于本文算法，且误检率和漏检率均要高于本文算法。其原因如下：1）随噪声点及干扰线条增加，Tao算法所采用的直线检测算法检测所得的直线段多为短直线，这使得在短直线合并过程中出错率增大，而造成无法检测出矩形。2）Tao算法将直线按倾斜角度分类并将其角度调整为同一角度，大大地降低了检测精度。

另外，作者采用文献［2］、文献［10］中算法进行本实验的检测，实验结果表明：在本实验中，这两种算法性能不佳。

实验2 图像检测实例

图7（a）为某卫星舱的布局扫描图，其大小为280×280，共含五个矩形和六个圆。对该图提取轮廓后如图7（b），再用本文算法来检测矩形，检测结果如图7（c）所示，检测时间为1.9s。因为该图像较为简单，采用Tao算法和文献［10］中算法均能检测到两个矩形，虽然这两种算法的检测速度要略快于本文算法，但两者的检测精度均要比本文算法低。

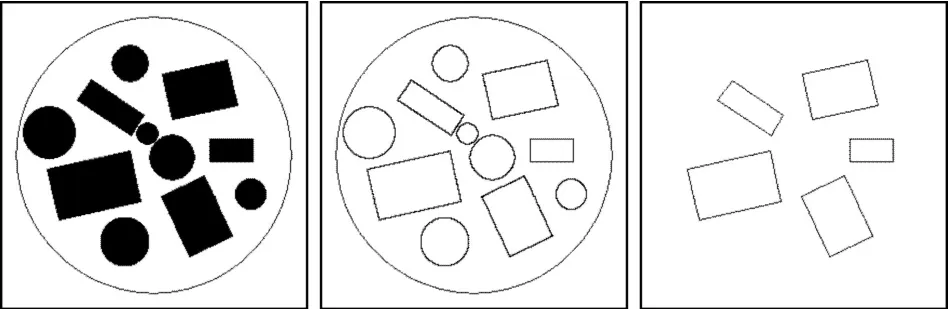
图7 图像检测实例

5 结语

针对矩形检测问题，本文提出了一种基于链码跟踪的矩形检测算法，该算法能较好地适应图像空间较复杂的情形（如矩形相交、杂乱线条较多、其他图形干扰较为严重等）。数值实验结果表明：本文算法具有较快的检测速度，可满足实时要求；并具有很高的检测精度，可满足精度要求。

［1］Zhu Y，Carragher B，Mouche F，Potter C.Automatic par⁃ticle detection through efficient Hough transforms［J］.IEEE Transactions on Medical Imaging，2003，22（9）：1053-1062.

［2］Clàudio Rosito Jung，Rodrigo Schramm.Rectangle Detec⁃tion based on a Windowed Hough Transform［J］.Proceed⁃ing of the XVII Brazilian Symposium on Computer Graph⁃ics and image Processing（SIBGRAPI'04）.

［3］Lagunovsky D，Ablameyko S.Straight-line-based primi⁃tive extraction in grey-scale object recognition［J］.Pat⁃tern Recognition Letters，1999，20（10）：1005-1014.

［4］Lin C，Nevatia R.Building detection and description from a single intensity image.Computer Vision and Image Understanding，1998，72（2）：101-121.

［5］Tao Wen-bing，Tian Jin-wen，Liu Jian.A new approach to extract rectangle building form aerial urban images［C］//In International Conference on Signal Processing，pages 143-146，2002.

［6］王佳，李波，徐其志.边缘检测中局部区域的动态阈值选取方法［J］.计算机应用研究，2010，27（2）：772-774.WANG Jia，LI Bo，XU Qizhi.Dynamic threshod selection based on local region in edge detection［J］.Application Research of Computers，2010，27（2）：772-774.

［7］覃勋辉，马戎，付维平，等.一种基于梯度的直线段检测算法［J］.光子学报，2012，41（2）：205-209.QIN Xunhui，MA Rong，FU Weiping，et al.A Line Seg⁃ment Detection Algorithm Based on Grad［J］.Acta Photon⁃ica Sinica，2012，41（2）：205-209.

［8］Grompone von Gioi R，Jakubowicz J，Morel JM，Randall G.，LSD：A Fast Line Segment Detector with a False Detec⁃tion Controll［C］//IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32（4）：722-732.

［9］刘景发，黄娟，蒋宇聪，等.基于Wang-Landau抽样的带静不平衡约束的简化卫星舱布局方法［J］.计算机科学.2016，12：287-292.LIU Jingfa，HUANG Juan，JIANG Yucong，et al.Packing Method Based on Wang-Landau Samplified Satellite Mod⁃ule With Static Non-equilibrium Constraints［J］.Comput⁃er Science，2016，12：287-292.

［10］ Zi-qiang Li.Generalized Hough Transform Fast Detec⁃tion for Hybrid Multi-Circle and Multi-Rectangle［C］//Proceedings of the 6thWorld Congress on control and Au⁃tomation， June 21-23， 2006， Dalian， China.10130-10134.

［11］王新，张元东，王莉.一种随机Hough变换检测圆的优化方法［J］.测控技术，2016，06：112-116.WANG Xin，ZHANG Yuandong，WANG Li.Optimiza⁃tion Method of Randomized Hough Transform to Detect Circle［J］.Measurement&Control Technology，2016，06：112-116.