化静为动 展开想象 提升学力——《三角形的认识》单元练习教学设计与说明

黄伟红

（本文作者系朱乐平名师工作站“一课研究”组成员）

【教学内容】

人教版四年级下册第五单元。

【教学过程】

一、连点成线，进一步理解三角形的意义

师：大家看，老师这里有两个点，把它们连起来会是什么图形？

生：一条线段。

师：如果再放上一点C，把它们连起来会是什么图形？

生：三角形。

师：你是怎么想的？

生：由三条线段围成的图形是三角形。

师：老师把点C放上去了，大家仔细看。（放在点AB之间）

生：不是三角形。

（教师继续放，把点C放在线段AB的延长线上）

生：不是三角形。

生：点C不能放在AB所在的直线上。

师：从点的角度看，怎样的三个点可以构成三角形？

生：不在同一条直线上的三个点可以构成三角形。

师：会形成什么样的三角形？

生：直角三角形、锐角三角形、钝角三角形、等边三角形、等腰三角形。

师：现在请你选其中一种三角形，去研究点C的位置。

【说明：给出两点，接着再增加一点，学生都认为是三角形，这是学生通过已有的知识与经验作出的思考，但发现同一直线上的点C摆放后并没有形成三角形，造成学生思维冲突，让学生自主感悟与体验连点成线，连线成面，进一步巩固“由三条线段围成的图形是三角形”这一概念，同时在思维冲突中进一步体会从点的角度描述三角形的意义，即“不在同一条直线上的三个点可以构成三角形”，这是学生在先前的学习中所没有接触的，让学生感悟可以从不同角度描述三角形的意义。】

二、动态变化，进一步体验各类三角形的特征与变换

（学生试画、交流、汇报）

1.直角三角形。

师：你画的是什么三角形？

生：直角三角形。

师：你把点C放在哪里了？

生：点A的正上方或正下方。

师：这样的点多吗？把这些密密的点连起来会是一条（直线）。

师：这条直线和AB是什么关系？（互相垂直）

师：点B这边呢？（同A）

师：要构成直角三角形，点C还可以放在哪里？

生1：三角板上的直角在这里（如下图），所以点C放在这里也是一个直角三角形。

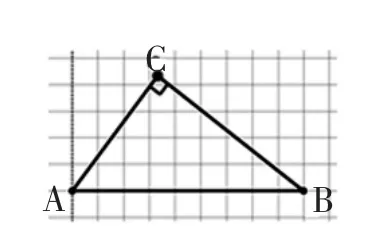
生2：是的，把三角板翻过来直角就在右边了，这样的点C左、右都会有很多。

师：大家观察一下，把这些点连起来好像是一条（圆弧）。

（课件呈现半圆形，并拖动点C，不断呈现直角三角形）

师：谁能用一句话归纳点C放在哪里可以构成直角三角形？

生：点C只要放在过点A或过点B垂直于AB所在的直线上（不包括点A和点B），或者放在圆弧上，就可以和AB构成一个直角三角形。

2.锐角三角形。

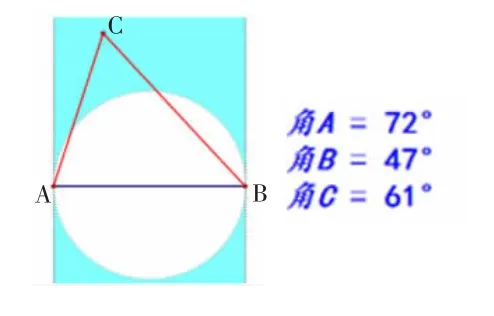
师：点C放在哪里可以构成锐角三角形？

生1：只要在圆弧的外面。（课件显示阴影区域。拖动点C在阴影区域的位置，显示△ABC三个角的度数，验证阴影部分的点C与AB确实构成锐角三角形）

3.钝角三角形。

师：点C放在哪里可以构成钝角三角形？

生：点C在白色区域中都可以。（课件演示。拖动点C在白色区域的位置，显示△ABC三个角的度数，验证白色部分的点C与AB确实构成钝角三角形）

4.等腰三角形。

师：如果要画出等腰三角形，点C又该放在哪里？

生：只要过AB中点作垂线，垂线上的每个点（除AB的中点）和AB连起来都是等腰三角形。

师：刚才我们把AB作为等腰三角形的底边，如果把AB作为等腰三角形的腰，另一条腰可以在哪里？（课件演示）

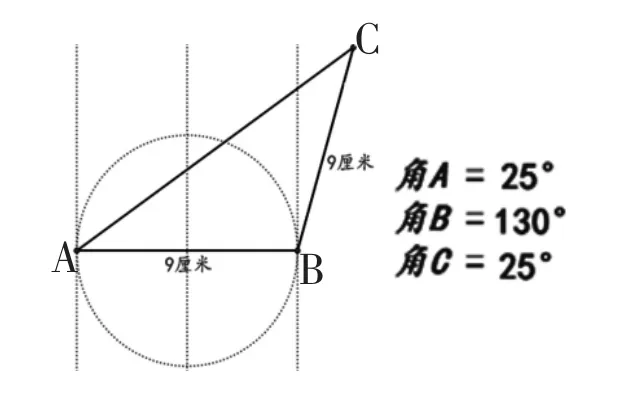
师：当AB作腰时，另一条腰BC可以在上面或下面。如果把点C画在左边也是同样情况。

5.等边三角形。

师：等边三角形有什么要求？（三边相等，每个角都是60°）

师：所以我们说等边三角形是特殊的等腰三角形。

【说明：给出固定两点，通过第三点的运动，让学生进一步感知各类三角形的特征及相互之间的关系，特别是几何画板的有效运用，让静态的点不断运动变化，让学生自主感悟出阴影区域的点和AB构成锐角三角形，白色区域的点和AB构成钝角三角形，而白色和阴影区域交界的点和AB构成直角三角形，体验了图形之间的变换，体会图形直观的研究方法、渗透分类思想、集合思想，同时让各部分独立知识连成片、结成网，进一步内化对三角形的认识。】

三、思维辨证，进一步深化三角形三边关系

师：刚才我们用三个点研究了构成三角形的各种情况，现在换个形式，如果给你两根小棒，能不能构成三角形？（出示两根小棒，分别长12厘米和14厘米）

师：用什么办法？（剪）怎么剪？（剪14厘米的）

师：为什么不剪12厘米的？

生：两边之和要大于第三边。

师：把14厘米剪成整厘米的两段你有多少种剪法？

反馈：1、13；2、12；3、11；4、10；5、9；6、8；7、7。

生：剪成1厘米和13厘米的不可以，因为两短边1厘米和12厘米之和是13厘米，而另一条长边也是13厘米。（课件演示）

师：刚才我们都是把14厘米的小棒剪成整厘米数的两段，还有其他剪法吗？（剪成小数）

师：这样也会有很多种剪法，如果我们把这么多种剪法拼成的三角形都放在一起会出现怎样的图形？课件呈现：

师：把这些三角形上面的顶点连起来，你看看像什么？

生：像国家大剧院，很美。

【说明：把两根小棒通过剪拼的方法拼成三角形，并在“剪哪一段”“怎么剪”“能否拼成”等不断辨析中，深化对三边关系的认识，同时渗透无限思想，并联系实际，把众多搭成的三角形叠放在一起，在欣赏国家大剧院的图片中感受数学的美，体会数学与生活的联系，感受数学的魅力。】

四、延伸拓展，进一步探究三角形角的知识

师：有一只瓢虫沿着三角形的边爬行，它怎么停下来了？

生：再爬下去的话就要出去了。

师：所以它在思考怎么办？（转身）它身体转过了哪个角？它又要转过哪个角？……

想一想：瓢虫沿着三角形边缘爬一周，身体一共旋转多少度？

生1：旋转一周就是360°。

师：你们发现它旋转一周又回到原来的位置与方向，所以是360°。还有其他方法吗？

生 2：180°×3-180°=360°，因为一个内角与瓢虫爬过的角合起来是180°，这样就有三个180°，减去三角形内角和180°，就是瓢虫身体旋转的度数。

生3：把这三个角剪下来能拼成一个圆。（课件演示）

师：你知道刚才瓢虫爬的是三角形的什么吗？（外角和）

【说明：通过瓢虫爬三角形的边这样一个富有童趣的问题，让学生猜想瓢虫转身的角度，在讨论、交流与辨析中，利用平角、周角、内角和等知识解决新问题，在加深原有知识的同时，拓展对三角形外角和这一新知的认识。】