自主探索为基石 方法引领为阶梯
——《梯形面积》教学实录与评析
2018-04-25执教赵姝蓉指导姜荣富
执教/赵姝蓉 指导/姜荣富
【教学内容】
浙教版五年级。
【教学过程】
一、回顾旧知,引入新知
师:还记得我们是用什么方法研究平行四边形面积的计算公式吗?那么三角形面积该怎么研究呢?
师:如果将三角形面积的研究方法分为两类,可以怎么分?
生:分为倍拼和割补两类。

师:虽然转化的方法不同,但都是转化成学过的平行四边形或长方形来研究的。
师:(出示一般梯形)今天我们一起来学习《梯形面积》一课,根据你们以往的学习经验,可以把梯形转化成什么图形?
(学生独立思考,发言)
【评析:导入部分回顾了平行四边形和三角形面积计算公式的探究方法,一方面梯形面积计算推导时要用到平行四边形和三角形的面积计算公式;另一方面,“转化”的思想是一脉相承的。将三角形面积探究的方法类化为倍拼和割补两种方法,“类化”对于梯形面积计算公式的探究是重要的铺垫。通过知识联系和方法类化,为后继学习积累经验,打好基础。】
二、动手操作,自主探究
1.独立操作,教师巡视。
师:老师在材料包里准备了一些梯形,请根据自己的想法转化成学过的图形。
(学生独立剪拼研究)
2.小组交流,准备汇报。
(1)说说自己是怎样转化的。
(2)补充别人没有的方法。
(3)推选代表进行汇报。
3.汇报方法,全班展示。
(学生展示剪拼的方法)
预设:②③④⑥⑧这些方法是学生比较容易出现的;没有出现的①⑤⑦⑨这些方法,可以电脑展示。
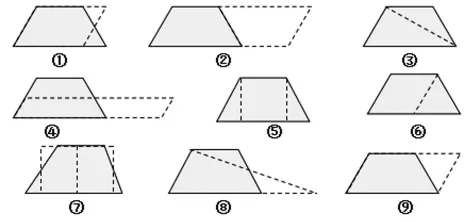
师:转化后图形的面积和原来梯形的面积有什么关系?
(倍拼的面积是原来梯形面积的两倍,其余的和原梯形面积一样,第9种例外)
师:转化后的哪一种图形最容易算出它的面积?
生:倍拼的图形最容易。
【评析:在这个环节,不给出具体的数据更加能突出图形转化的重点,学生通过独立操作,研究、展示出各种转化方法。其中一部分是很容易看出如何转化的,也有一部分是不容易看出来的。对于不容易看出来的,请学生谈谈想法,相互交流,互相启发,使其方法多样化。】
4.计算面积,归纳公式。
师:你能算出②号平行四边形的面积吗?
生:不能,没有数据。
师:如果只给你梯形的数据,行吗?(行)那你们觉得需要梯形的哪些数据呢?
(教师给出数据:上底3、下底 7、高 4和腰 5)
师:现在怎样计算平行四边形的面积?怎样计算梯形的面积?
板书:S梯=(3+7)×4÷2=20
师:这个算式里的各部分分别表示转化后图形的哪个部分?
生:3+7表示转化后平行四边形的底,4表示转化后平行四边形的高。
师:请从剩余的转化方法中,选一种求转化后的图形面积。
(1)学生选择数据,计算转化后图形的面积。
(2)反馈梯形面积计算的算式和结果。
师:观察②④⑧这三种图形的计算算式有什么共同点?
生:都可以整理成为S梯=(3+7)×4÷2=20。
师:通过转化和计算发现梯形的面积与什么有关?
生:上底、下底和高。
师:通过刚才的活动,可以总结出怎样计算梯形的面积?
生:S梯=(上底+下底)×高÷2。
师:观察③,因为转化后图形的面积也是20,说明你们的方法都是正确的,只是每种算式的表达形式不同,你们能整理成这样的表达方式吗?
师:那么这里的(3+7)表示什么?
生:上底加下底。
师:看样子在计算梯形面积的时候和什么无关?
生:和两个腰无关。
(3)如果我们现在用a来表示上底、b表示下底、h表示高,你能用算式来表示梯形的面积吗?
学生尝试用字母表示:S=(a+b)×h÷2
(4)课外补充:展示学生没有讨论到的推理方法,鼓励学生课后继续研究。
【评析:给出梯形的上底、下底、两腰和高的完整数据,由学生自己选择有用的数据计算转化后图形的面积,这样的经历让学生充分感受到梯形的面积计算公式与上底、下底和高有关。整体呈现转化图形和相应的面积算法,引导学生归纳、概括出梯形面积计算公式:S=(上底+下底)×高÷2。其中分割成两个三角形的转换方法,分割很容易,但是算式推导对学生有些困难,因为这里需要用到乘法分配律来提取公因数(高)。因此,我们把两个三角形的转换放在最后展开:第一,有了前面几种的归纳和结果的相等,学生必然会有所猜想;第二,通过计算结果相等,也方便学生验证推理。在学生转化和推导的基础上,水到渠成地提出用a来表示上底、b表示下底、h表示高,从而得到S=(a+b)×h÷2。】
三、应用公式,梳理沟通
1.出示各种梯形,填表练习。

(1)独立完成后,集体反馈。
(2)总结,强化梯形面积的计算公式。
(学生如有困惑,可以任选一个通过数方格验证)
2.对三角形、梯形、平行四边形面积公式进行沟通联系。
师:今天我们研究了梯形的面积计算公式,之前我们还学习了三角形和平行四边形的面积计算公式。它们之间有什么联系?
(课件演示,引导学生直观理解当 b=0 时,S=ah÷2)
师:梯形的面积计算公式和平行四边形的面积计算公式有什么联系?
(课件演示,引导学生直观理解当 a=b 时,S=ah)
【评析:最后的环节没有设计应用公式解决实际问题,还是放在数学情境内,主要是“直接应用公式”和“梳理沟通公式”。第一,应用公式求取方格图中的梯形面积,一方面可以巩固梯形公式,另一方面方格有助于学生将面积计算公式和面积的本义(单位面积的个数)联系起来;第二,将平行四边形、三角形和梯形的公式进行沟通,不仅对于单元课之间有所呼应,更重要的是,这样的梳理沟通蕴含着“极限”的思想,为后继学习圆面积公式的推导做准备,较好地发展了学生的空间观念。】
【课例综述】
虽然从整体上看这节课并没有跳脱图形课从问题情境——推导公式——应用公式的传统模式,但从细节上看这节课每个环节的设计都有独特的理解和理念在支撑,特别是充分展开公式的推导过程,甚至在练习中强调对于公式的多样化的理解,值得品味。
1.图形联系,巧妙回顾。从回顾平行四边形面积和三角形面积的探究方法引入本课,到让学生类化三角形面积的探究方法,一方面避免了简单的再认回忆,另一方面在众多的方法中进行分类是一种更高层次的思维方式。这种对知识的回顾是有一定的教学增量的,也为后继的学习做好充分的准备。
2.探索方法,分层推导。在梯形面积推导的过程中,经历用分、合、移、补等方法探索梯形面积计算方法的过程,让学生经历方法的交流诠释、转化沟通、抽象概括过程,培养学生的逻辑思维能力,发展学生的空间观念。对于多样的转化方法,从学生的角度考虑,有意识分层、分类交流与推进,很好地处理了学生自主学习和教师主导深入之间的关系。各种方法显得多而不乱,既概括共性,生成普遍的算法 S=(a+b)h÷2,又张扬个性,不同的人对公式有不同的理解。
3.极限思想,整合沟通。通过动态的多媒体演示,渗透极限思想,把平行四边形、三角形和梯形面积计算公式沟通整合:当b=0时,梯形转变为三角形,面积公式为 S=ah÷2;当 a=b时,梯形转变为平行四边形,面积公式为S=ah。这一联系打通了三种图形面积之间的隔阂,沟通了算法联系,给学生新鲜的经验和角度。而这种用联系的观点看问题的思想、理念,也为学生后续的学习,特别是形成良好的认知结构奠定了基础。
