基于Lyapunov直接法差动驱动机器人控制算法研究

，，

(上海工程技术大学 机械工程学院，上海 201620)

0 引言

近年来，非完整移动机器人的运动控制技术已经成为机器人领域的研究热点，是实现轮式机器人智能化可靠行驶的重要保证，也是实现自主导航的前提和基础，具有广阔的应用前景和市场价值。根据控制方法不同分为点镇定控制[1]和跟踪控制[2-3]，点镇定控制是为机器人系统设计控制律，使其能够到达运动平面上任意给定目标点，并且能够以预期的姿态稳定在该目标点；跟踪控制所设计的控制律可以使机器人能够到达并以一个给定的速度跟踪平面上某条轨迹。镇定控制与跟踪控制原理不同，因此在实际应用中常根据不同的问题来设计不同的控制器。

以步进电机驱动的差动驱动轮式机器人为研究对象，首先建立运动学模型和动力学模型，设计了一种基于Lyapunov直接法的运动学轨迹跟踪控制器；然后根据动力学模型引入速度、加速度限制策略；仿真结果证明该控制器具有较快的收敛速度和较高的稳定性，在轨迹发生变化时也能迅速做出调整；最后将控制算法的脉冲参数编译下载到STM32F407进行实验，获得了较好的结果。

1 轮式机器人数学模型

1.1 运动学模型

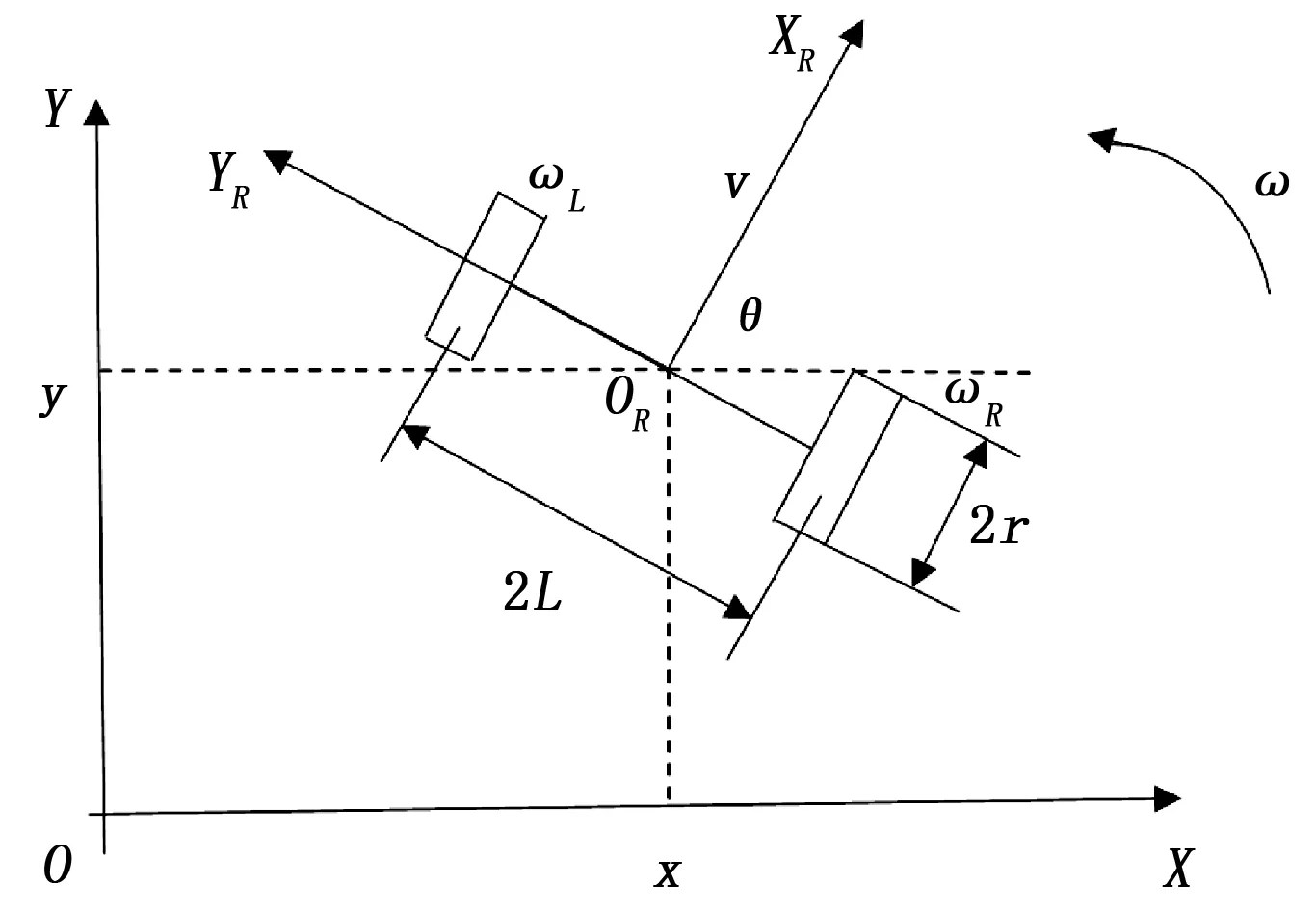
图1 运动学示意图

(1)

由约束方程(1)可知，不能通过积分得到x，y与θ的关系，这是典型的非完整约束系统。

根据运动学原理还可以得到：

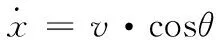
(2)

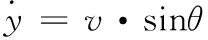
(3)

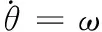
(4)

(5)

(6)

由式(2)～(6)可以建立非完整移动机器人的运动学模型：

(7)

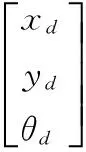
(8)

结合公式(2)(3)(4)，经过推导可得到机器人位姿误差的微分方程：

(9)

1.2 动力学模型

一般情况下，具有n维系统状态移动机器人模型可以用非完整约束的广义力学系统来描述，根据拉格朗日力学分析方法，建立动力学模型[4]：

(10)

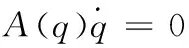
(11)

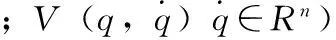
(12)

设机器人的质量为m，机器人相对于点OR的转动惯量为J，左右两驱动轮的驱动力矩分别为TL、TR，令驱动轮向机器人前进方向转动时驱动力矩为正，向机器人后退方向转动时驱动力矩为负。对图1进行受力分析，得到点OR处的广义驱动力向量：

(13)

公式(13)中fx为驱动力在X轴向分量，fy为驱动力在Y轴向分量，fθ为使机器人旋转的力矩。当ω>0时，机器人由于离心力的作用有向轴负向ORYR发生侧滑的趋势，因此约束力λ指向ORYR轴正方向，根据牛顿第二定律建立系统动力学方程：

(14)

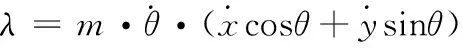
(15)

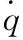
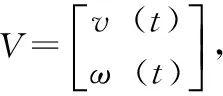
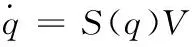
(16)

对公式(16)求导可得：

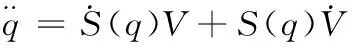
(17)

将公式(17)代入公式(12)可得：

(18)

公式(18)等号两边同时左乘ST(q)，可以消去AT(q)λ项，经过推导可得：

(S(q)TM(q)S(q))-1S(q)TB(q)τ

(19)

将S(q)，M(q)，V，B(q)τ的结果代入公式(19)最终可得：

(20)

2 Lyapunov直接法控制器设计

轮式移动机器人控制系统原理结构框图如图2所示，其中控制输入量Vc=[vc,ωc]T，P表示机器人实际位姿，Pd表示机器人期望位姿，Pd-P为机器人在绝对坐标系XOY下的位姿误差，经过旋转矩阵的作用转化为在机器人局部坐标系XRORYR下的位姿误差Pe。采用Lyapunov直接法设计运动学控制器，构造能量函数[5]：

(21)

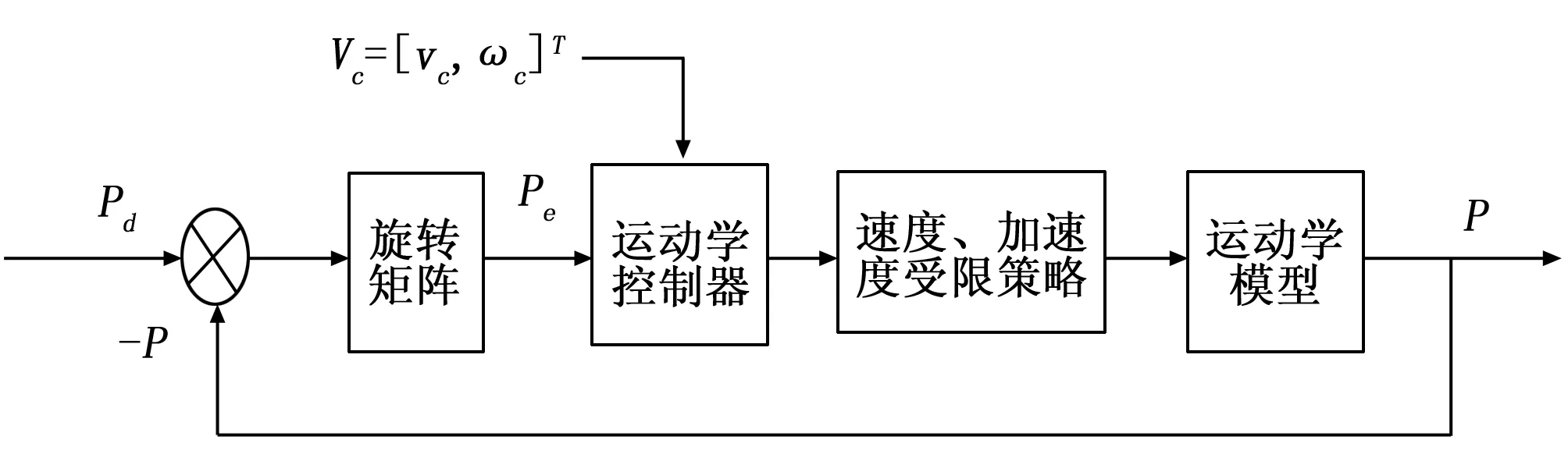
图2 机器人控制结构原理图

其中：k1>0且有界，则公式(21)为正定函数，L对时间t求导并结合公式(7)、(8)、(9)可得：

(22)

取控制律:

(23)

其中：k2,k3>0有界。

联立公式(5)、(6)、(23)得：

(24)

将控制律(23)代入公式(22)可得：

(25)

通过控制器的作用最终会使Pe趋于0，则有θe→0，将sinθe泰勒级数展开，公式(25)可转化为：

(26)

控制律(23)中vc主要是为了消除移动机器人前进方向上的位置误差xe，其中vdcosθe为机器人前进方向上因期望线速度vd产生的位移；k3θe项对θe的导数要大于等于k3sinθe对θe的导数，因此该控制律要比使用kesinθe作为参数的控制律对姿态角误差θe调节更加迅速。

3 仿真分析

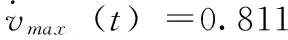
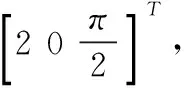
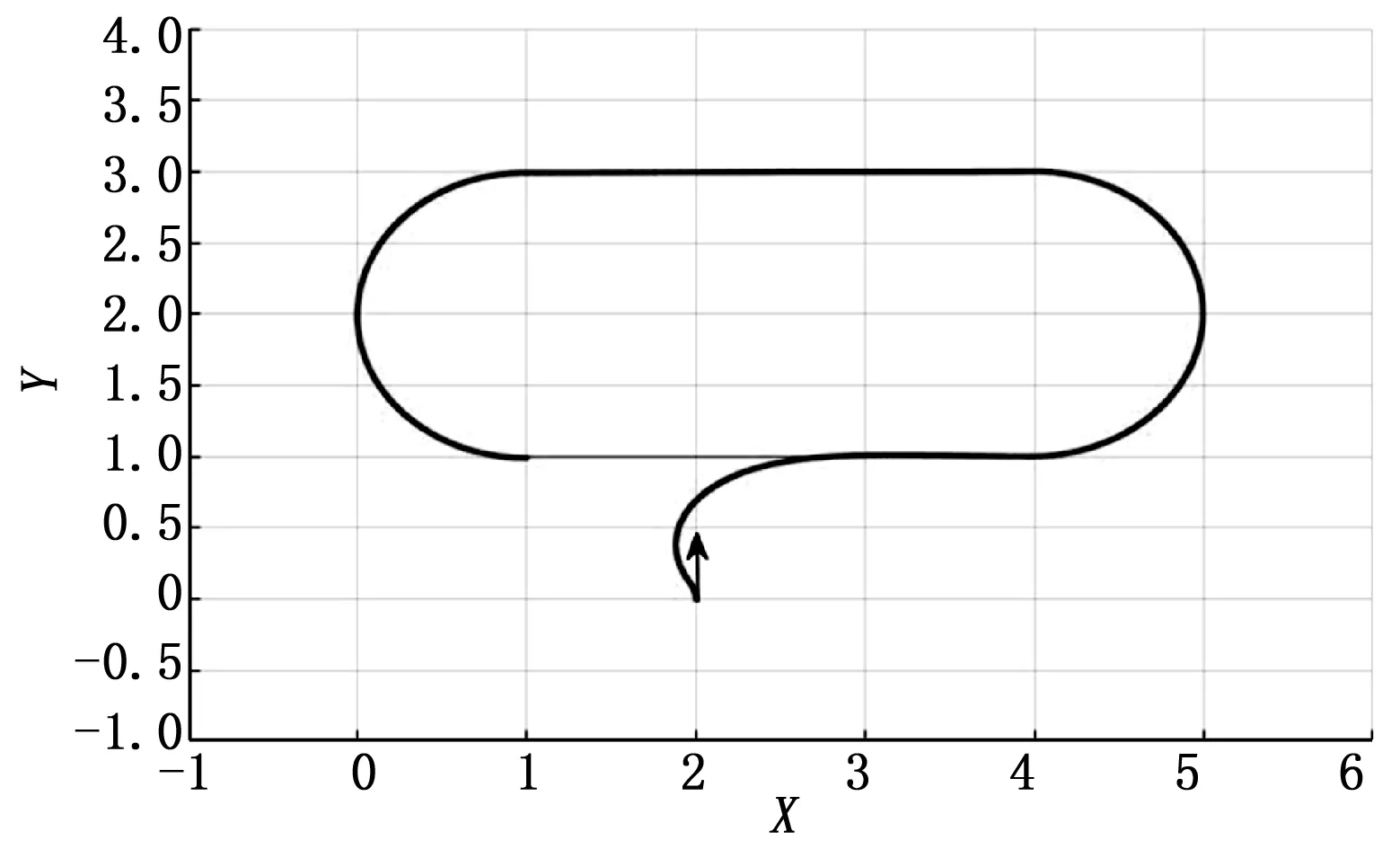
图3 轨迹跟踪情况

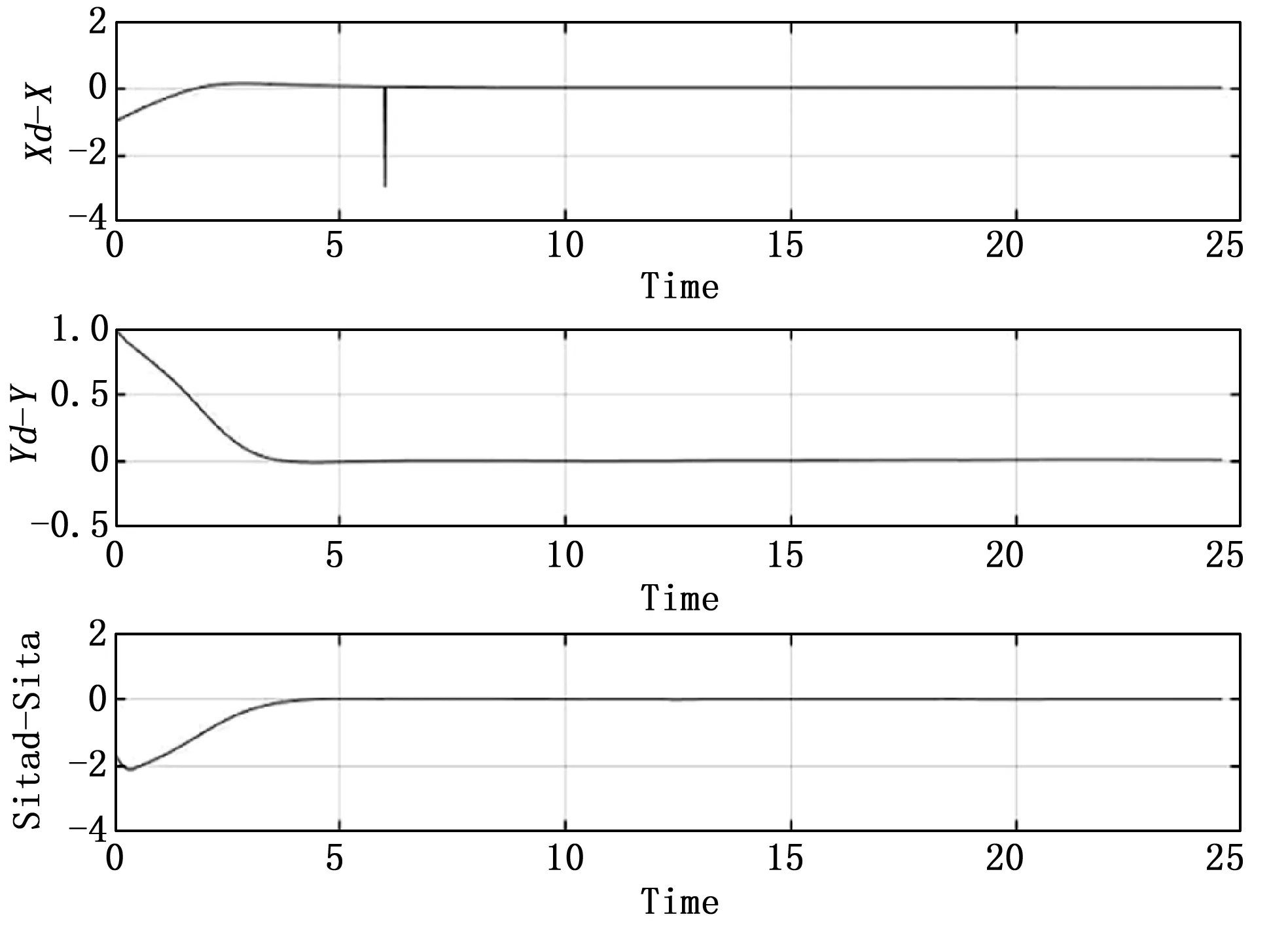
图4 位姿误差

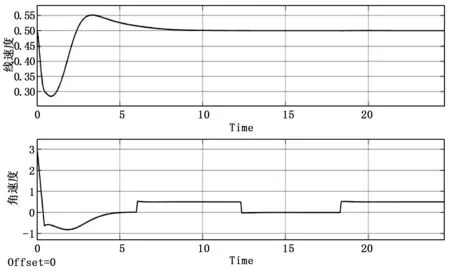
图5 线速度和角速度的变化曲线

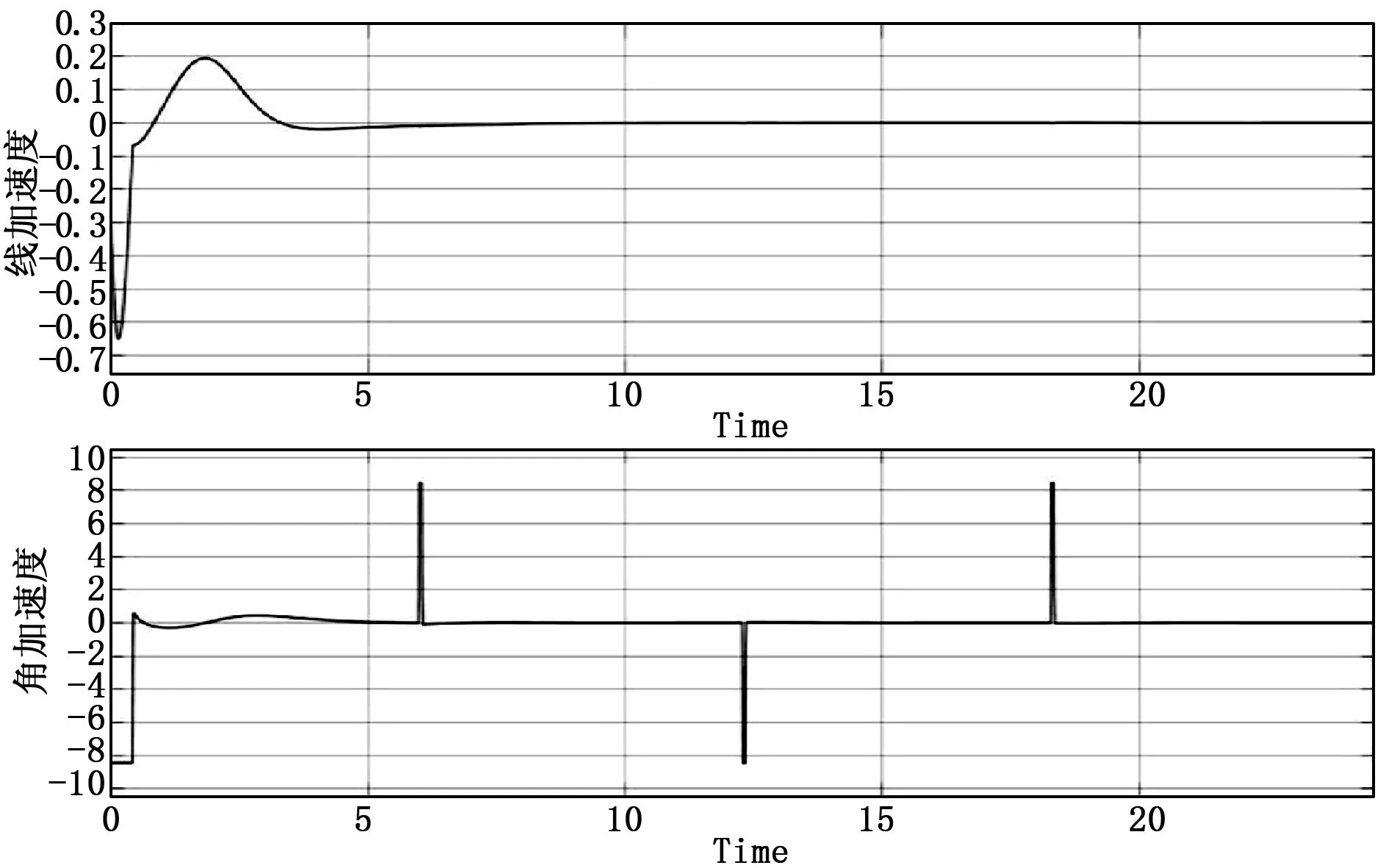
图6 线加速度和角加速度变化曲线

仿真中期望轨迹为直线轨迹和曲线轨迹的结合，使得机器人在期望轨迹上有角速度的变化，在这种情况下机器人也能稳定地跟踪运动，并且在轨迹的变化处能快速做出响应。通过仿真结果可以看出，初始位姿误差在4 s内完成收敛，调节速度快，在收敛的过程中没有发生速度突变，且收敛后有良好的稳定性，除第一次转弯处由于线速度v>0.5 m/s使得xd-x出现一次负向跳动，之后的转弯处线速度稳定在0.5 m/s，所以位姿误差基本稳定在0值没有再次发生跳变。由于加入速度和加速度限制策略，使得速度、加速度在有限范围内变化，通过图6可以得到角加速度始终被限制在[-8.428 8.428]范围内，保证了步进电机较高的工作性能和控制精度。

4 实验验证与分析

结合支持Simulink的第三方硬件库，如图7所示，采用基于模型的程序设计方法，将脉冲数据编译下载到STM32F407微控芯片中。由于机械装配存在误差，机器人转动惯量无法精确计算等因素，编译下载前需要将控制算法生成的脉冲数据结合实际情况进行小范围的修正。利用ULN2003驱动板将STM32F407对应引脚输出的3.3 V信号电压转换为步进电机驱动器额定信号电压5 V，通过相应的电路连接在机器人平台上进行实验。

取图3中(2,0),(1,1),(2.5,1),(4,1),(5,2),(4,3),(2.5,3),(1,3),(0,2)等9个坐标点为标记点分别标号0-8，如图8所示布置实验场地。经过实验，机器人运行状态良好，在期望时刻与对应标记点的位姿误差较小，控制算法生成的脉冲数据准确度高，而且可以较方便地将控制算法计算结果应用于微控制芯片。

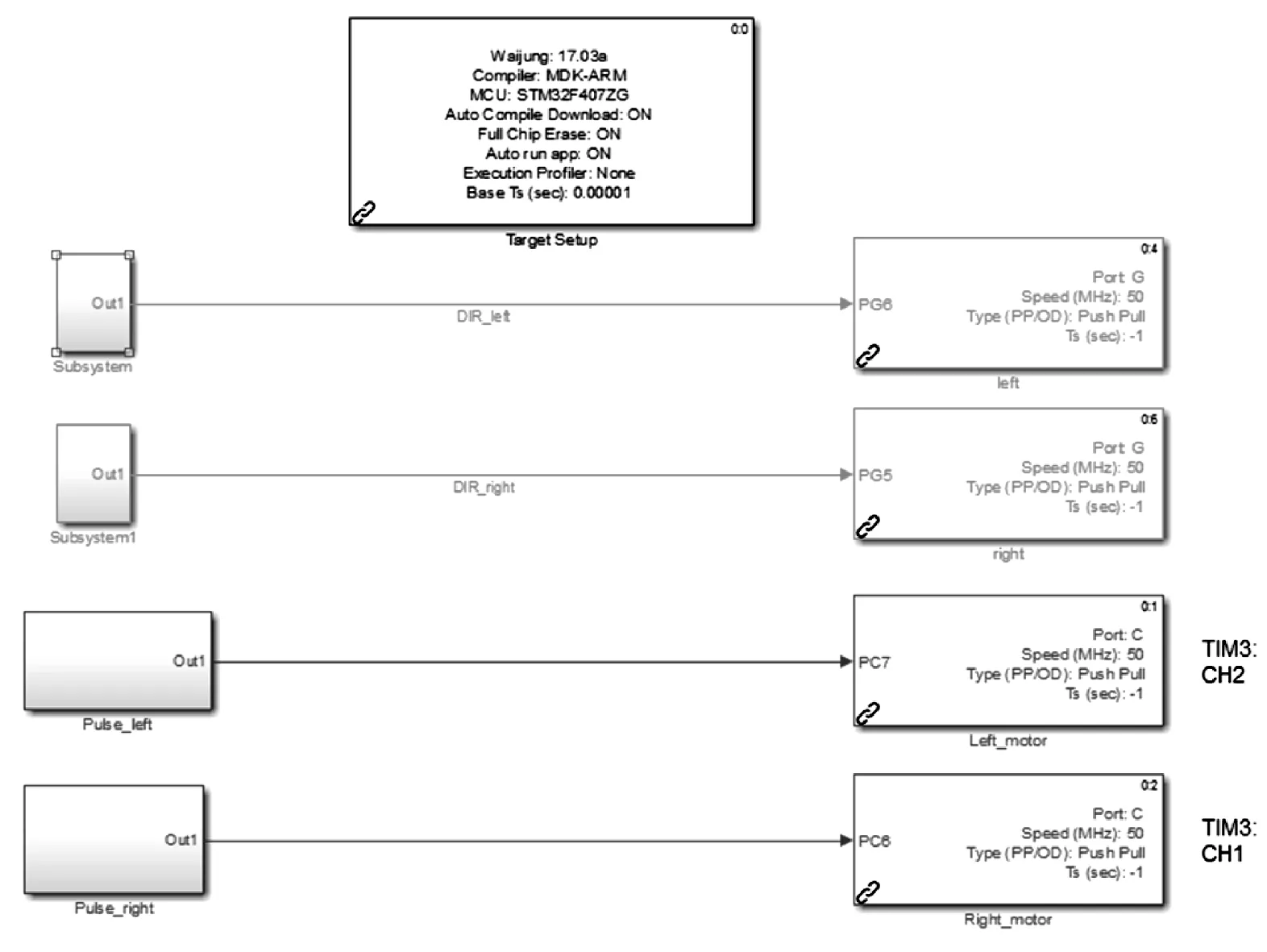
图7 程序模型

图8 标记点示意图1

5 结论

以步进电机差动驱动轮式机器人为研究对象，通过建立运动学模型，利用Lyapunov直接法设计了运动学控制器；通过建立动力学模型并结合步进电机工作特点，设计了对运动学控制器中线速度、角速度、线加速度、加速度的限制策略，最终实现了对机器人的运动控制；经过仿真和实验，证明所设计的控制器具有较高的跟踪精度和稳定性，机器人对初始位姿误差矫正时间短，在轨迹变化处能做出较快响应；结合matlab硬件支持包，采用基于模型的程序设计方法可以将理论分析计算结果应用于实践，缩短了开发周期。

参考文献：

[1] 曹政才，赵应涛，吴启迪. 基于Bcakstepping和神经动力学的非完整移动机器人点镇定[J]. 电子学报，2011，39(3)：591-595.

[2] 马建伟，石佳玉. 非完整约束移动机器人的轨迹跟踪控制[J]. 计算机测量与控制，2017，25(3): 77-80.

[3] 金 娟，王耀南. 基于模糊CMAC的移动机器人轨迹跟踪控制[J]. 计算机工程与应用，2015，51(1): 54-58.

[4] 杨 敏. 轮式移动机器人控制算法研究及其伺服系统设计[D]. 南京：南京航空航天大学，2014

[5] 李 平，王建锋，李 娜，等. 基于Lyapunov直接法的移动机器人运动控制研究[J]. 中国科技论文，2016，11(2)：160-163.