在变化中寻求不变——以图形的平移、折叠与旋转为例

赵 军（特级教师）

平移、折叠和旋转是几何中的三种基本变换，运用这三种变换所命制的试题往往灵活多变，具有一定的挑战性.如何在变化中寻求不变的思路？下面笔者以近两年的中考试题为例进行剖析，希望对大家的学习有一定的借鉴作用.

一、平移变换

例1 （2016·上海虹口模拟）如图1，已知△ABC中，AB=AC=5，BC=6，将△ABC沿射线BC方向平移m个单位得到△DEF，顶点A、B、C分别与D、E、F对应，若以点A、D、E为顶点的三角形是等腰三角形，且AE为腰，则m的值是_____.

图1

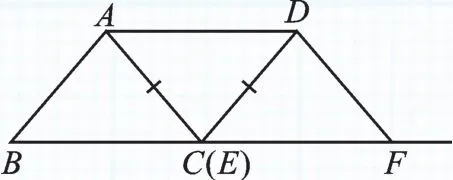
图2

【分析与解】本题中变化的是△DEF的三个顶点，如何在平移的运动过程中找出“AE=DE或AE=AD”时的两个静态的位置是解题的关键，我们可以通过动手操作，在△ABC平移的过程中将两种符合要求的图形画出，并在此基础上求解.

如图2，当AE=DE时，B点平移至E点，此时m=6；如图3，当AE=AD时，平移的距离为AD或BE的长，过点A作AG⊥BE，垂足为G，由题意，AD=AE=BE=m，在等腰三角形ABC中先求得BG=3，则AG=4，GE=m-3，在Rt△AGE中，AG2+GE2=AE2，即42+（m-3）2=m2，所以，故m的值为6或

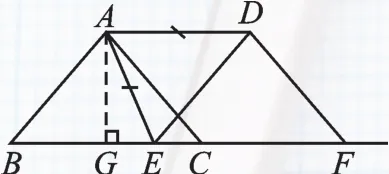
图3

【反思】平移变换是三大变换中较为简单的一种变换，需要我们主动“动手”操作，在不同的位置，通过试验找出适合的图形，抓住平移前后不变的量，并在此基础上结合方程等知识解决问题.

二、折叠变换

例2 （2017·扬州）如图4，把等边△ABC沿DE折叠，使点A恰好落在BC边上的点P处，且DP⊥BC，若BP=4cm，则CE=____cm.

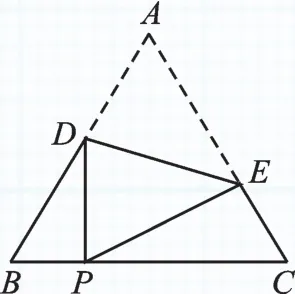
图4

【分析与解】由已知条件可得两方面的结论：①∠B=∠C=∠DPE=60°，结合DP⊥BC能得到∠CPE=30°，并在此基础上得到∠PEC=90°，也可以得到△BPD∽△CEP；②在Rt△BPD中，∠B=60°，BP=4，能得到BD和PD的长.结合折叠、含30°的Rt△PCE或相似求得EC的长.

方法1：在Rt△BPD中，易求得BD=2BP=8，PD=43，由折叠得AD=PD，∴AB=8+43，

方法2：在求得PC=4+43后，可由△BPD∽△CEP求得：CE=2+23.

【反思】“折叠出全等，全等出相等”.抓住折叠前后不变的边和特殊的角，结合直角三角形、“一线三等角型”的相似模型均可打开思路，寻求到解决问题的突破口.

三、旋转变换

图5

【分析与解】本题有两个特别之处，①是曲线l比较特殊，它是由函数在第一象限内的图像旋转得到的；②是A、B两点的坐标比较特殊，横坐标、纵坐标均含有数值 2，所以这两点都在象限角的角平分线上，即OA、OB与x轴和y轴的夹角均为45°.故有两种解题思路可以尝试.思路1，如图6，恢复原来的图形，将现在的图形整体绕点O顺时针旋转45°，回到我们熟悉的图形上来，然后用S△OAN-S△OAM即可（也可用S△OBM-S△OBN或S△OAB-S△OAM-S△OBN）；思路2，如图7，连接OA、OB，建立新的坐标系xOy′，用同样的方法予以解决.

图6

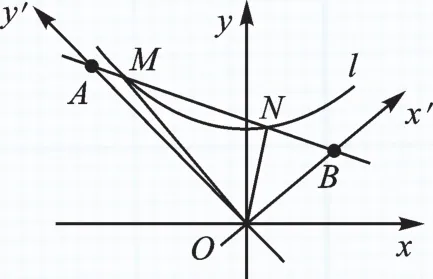
图7

【反思】无论将图形恢复为我们熟悉的图形，还是建立新的坐标系，求△OMN的面积都要先求出点M、N的坐标，然后利用三角形面积的差求解，体现了方程思想和转化思路.

小试牛刀

图8

图9

图10

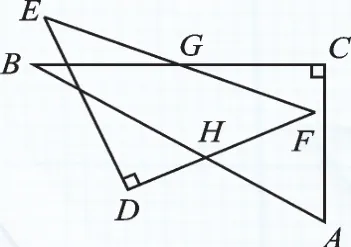
图11

2.如图9，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC上，以AD为折痕，将△ABD折叠得到△AB′D，AB′与边BC交于点E.若△DEB′为直角三角形，则BD的长是_______.

3.一副含30°和45°角的三角板ABC和DEF叠合在一起，边BC与EF重合，BC=EF=12cm（如图10），点G为边BC（EF）的中点，边FD与AB相交于点H，此时线段BH的长是______.现将三角板DEF绕点G按顺时针方向旋转（如图11），在∠CGF从0°到60°的变化过程中，点H相应移动的路径长共为______.（结果保留根号）