规范答题,提高考试成绩
2018-04-25何广谋
何广谋

2017年的中考已落下帷幕,从答题情况来看,特别是解答题,不少同学出现了会做的题目做不对,解对的题目写不全的现象,从而丢掉了一定的分数,这不能不让人感到遗憾.针对这种情况,本人结合2017年中考命题的经验和“圆”这一章节相关知识点,列举典型的、有代表性的中考题来说明如何规范答题.
和“圆”相关的解答题在数学中考当中的分值一般为10分的中档题或者12分的综合题,下面我就以这两个分值的题举例说明.
类型一:10分的中档题
1.设计有两个问题的.
例1 (2017·阿坝州)如图1,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若 AC=6,BC=8,OA=2,求线段 DE的长.
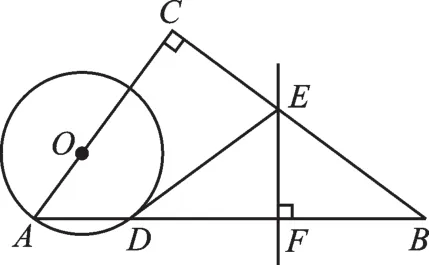
图1
【分值猜想】本道题有两个问题,一个证明一个计算,既考查说理又考查计算能力是一种常见的组合方式,这样的10分题通常每问5分.
【考点】直线与圆的位置关系;线段垂直平分线的性质.
【分析】(1)直线DE与圆O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;(2)连接 OE,设DE=x,则 EB=ED=x,CE=8-x,在直角三角形OCE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出DE的长.
【解答】(1)直线DE与⊙O相切.(1分)
理由:连接OD,
∵OD=OA,∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED,∴∠B=∠EDB,
∵∠C=90°,∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°-90°=90°,
∴直线DE与⊙O相切.(5分)
(2)连接OE,
设DE=x,则EB=ED=x,CE=8-x,
∵∠C=∠ODE=90°,
∴OC2+CE2=OE2=OD2+DE2,
∴42+(8-x)2=22+x2,(8分)
解得:x=4.75,
则DE=4.75.(10分)

图2
【注意】通常情况下,像第一问中判断直线与圆的位置关系这样的问题,只要回答正确也是能得1分的,所以同学们千万不要忽视.
2.设计有3个问题的.
例2 (2017·扬州)如图3,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.

图3
(1)判断直线DE与半圆O的位置关系,并说明理由.
【分析】(1)结论:DE是⊙O的切线.由平行四边形OABC易证∠OCE=90°,即可解决问题⁀.(⁀2)①连接 AC,证得∠BCA=∠FAC,得出即CF=AB,可得结论;②只要证明△OCF为等边三角形即可解决问题.
【解答】(1)DE与半圆O相切.(1分)
理由:∵CD⊥AB,∴∠D=90°.
∵在▱ABCO中,∴OC∥AD,
∴∠OCE=∠D=90°,
∴OC⊥DE,又∵OC是半圆O的半径,
∴DE与半圆O相切.(4分)
(2)①证明:∵在▱ABCO中,
连接AC,则∠BCA=∠FAC,∴
∴CF=AB=OC,(7分)
②∵CF=OC=OF,
(2)①求证:CF=OC;②若半圆O的半径为12,求阴影部分的周长.
【分值猜想】本题满分10分,共两大问,3个小问题.在解题过程中,我们为了不丢分,应猜测一下这个10分怎样分配.在正常情况下结论猜测正确的可以获得1分,这样还有9分,刚好分配给3个问题.所以在解题过程中我们就不能遗漏第1问的结论分,即使不会说理,也可以通过猜想得到分数.
【考点】直线与圆的位置关系;平行四边形的性质;弧长的计算.

图4
∴△OCF为等边三角形,∴∠COF=60°,
∴在Rt△OCE中,
CE=3OC=123,OE=2OC=24,

∴C阴影部分=EF+CE+lC⁀F=12+124π.(10分)
类型二:12分的压轴题
这类题目一般都是由3个问题构成,问题难度呈逐渐上升趋势,入手易,但完整解题较难.
例3 (2017·烟台)如图5,菱形ABCD中,对角线 AC,BD 相交于点 O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
(1)求BF的长(用含有t的代数式表示),并求出t的取值范围.
(2)当t为何值时,线段EN与⊙M相切?
(3)若⊙M与线段EN只有一个公共点,求t的取值范围.

图5
【分值猜想】本题有3个问题,可猜想每问4分或3分、4分、5分.
【考点】圆的综合题.
(2)当线段EN与⊙M相切时,易知△BEN∽△BOA,可得解方程即可.
【解答】解:(1)连接MF.
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,OA=OC=6,OB=OD=8,
∵MB=MF,AB=AD,
∴∠ADB=∠ABD=∠MFB,
∴MF∥AD,
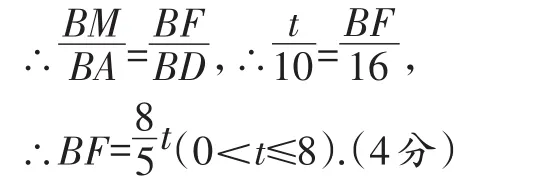
(2)当线段EN与⊙M相切时,易知△BEN∽△BOA,∴

图6
通过上面的举例,不难看出,只要我们在平时的练习中,经常分析考点,猜想分值,就会在解题过程中,知道怎样按考点规范解答,不跳步骤,做一步就能得一分,甚至不会做的也可以从考查方向上解答,尽量多得分,这样在中考答题中才不会留下遗憾.
