基于Einstain算子的压裂改造模糊综合评判
2018-04-24李海阔杨聪萍
李海阔 杨聪萍


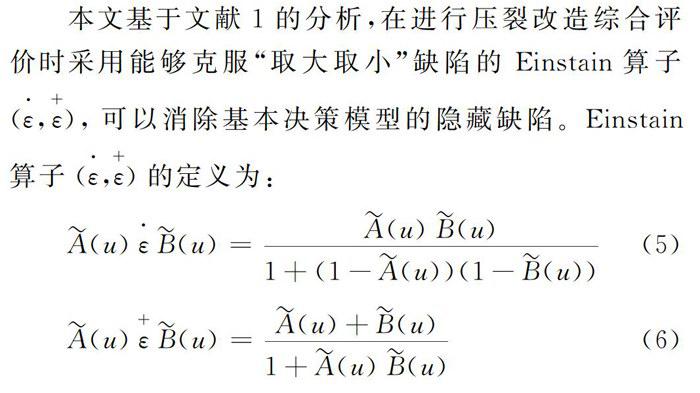
摘 要:水力压裂技术的迅速发展与广泛应用使得经济、准确地对地下压裂效果进行评估以指导优化改造显得十分必要。传统的压裂评估方法难以达到优化改造的效果。通过引入模糊综合评判理论,建立压裂综合评估的模糊评判模型,同时基于非线性Einstain算子求解模型,并对压裂相关参数进行模糊综合评价,分析压裂改造措施。在实际压裂井的基于构建的模糊综合评判模型并采用非线性Einstain算子计算,评判结果为影响裂缝长度的主要原因为压裂液的选择,与基于其他四种模糊算子的评判结果进行对比表明,所提出的压裂改造评价方法有效可行。
关键词:水力压裂;优化改造;模糊综合评判;Einstain算子
0 引言
压裂改造措施分析及优化是综合压裂工艺评价、储层产能与改造前景评价的产物。它是为实现储层产能与改造前景评价的目标,对所需的压裂可控制参数(如裂缝长度、裂缝导流能力、裂缝高度、裂缝沟通水层的程度、压裂液对地层的污染程度等)进行分析与优化,针对现有的压裂工艺评价结果,提出再次施工改造时的措施、施工环节调节的措施,指导下一步的生产工作。
现有的很多压裂评估技术一般费用较高而且技术复杂。近几年,模糊综合评判方法在各个领域中得到了广泛应用,显示了其独特的优越性。但使用该方法得到的结果有时会出现不合理或失效现象,尤其是在Zadeh算子下得到的结果。针对目前普遍使用的模糊综合评判方法,文献等都研究了其在实际应用中的失效性,提出了各自的改进方法。本文结合文献提出的改进方法,建立的压后模糊综合评判模型,得到很好的效果。
1 模糊综合评判
1.1 模糊评判模型
设评价对象有m个因素,所有因素組成的集合表示为论域U={u1,u2,…,um},称为因素集。对于各个因素可能取得n个评价,构成的评价集用论域V={v1,v2,…,vm}表示。
对于评价对象的每一个因素ui都有一个模糊评价集合R={ri1,ri2,…,rin},可视为V上的一个模糊子集,表示为RiF(U×V)。m个因素共有m个模糊决策集合,可以用模糊矩阵表示为:
R=R1 R2 … Rm=r11r12…r1n r21r22…r2n ……… rm1rm2…rmn
建立(U,V,R)三元体构成的模糊综合评判的数学模型:
(1)因素集 U={u1,u2,…,um}
(2)评价集 V={v1,v2,…,vm}
(3)构造模糊变换
TR:F(U)→F(V)(1)
AAR(2)
其中,R为U到V的模糊关系矩阵R=(rij)m×n。
1.2 模糊运算
若评价对象m个因素的权重分配集合为A={a1,a2,…,am},则可以得到模糊决策矩阵B,其结果由下式可以求出:
B=AR(3)
注:算符“”表示模糊运算。
在广义模糊运算中,模糊决策矩阵B的第j项的计算式为:
bj=(a1r1j)Δ(a2a2j)Δ…Δ(amamj) (4)
其中,1≤j≤n。
注:算符“”表示广义模糊“与”运算,“Δ”表示广义模糊“或”运算。
由此运算所得的模糊决策模型记为。基于模糊综合评判的基本决策模型一般有:M(∧,∨),M(·,⊕),M(·,∨),M(·,+)和Einstain算子(ε·,ε+)等。
2 模糊评判算子
在模糊系统的应用中,基本运算的算子选择是一个重要的问题。
文献1-3对类似M(∧,∨)的“取大取小”算子的失效性作出了分析,在基本决策模型中简单的“取大取小”算子只使用了一个或几个因素,而对于其它因素根本不起作用。往往在处理数据时“淹没”了有效的数据,遗漏了有用的信息,以至于得到的结果理论上有所欠缺,实际应用效果不佳。
本文基于文献1的分析,在进行压裂改造综合评价时采用能够克服“取大取小”缺陷的Einstain算子(ε·,ε+),可以消除基本决策模型的隐藏缺陷。Einstain算子(ε·,ε+)的定义为:
A(u)ε·B(u)=A(u)B(u)1+(1-A(u))(1-B(u))(5)
A(u)ε+B(u)=A(u)+B(u)1+A(u)B(u)(6)
3 模糊评判实际应用
3.1 评判结果
对于压裂改造措施进行评价,在众多压裂因素中选取5个显著影响压裂效果的因素:裂缝长度、裂缝高度、裂缝导流能力、裂缝闭合压力和裂缝表皮系数;相应的评价集的指标定为5种改造方式:施工规模、施工排量、施工砂比、压裂液选择、支撑剂选择。
即是,(A)(裂缝长度、裂缝高度、裂缝导流能力、裂缝闭合压力、裂缝表皮系数),A (施工规模、施工排量、施工砂比、压裂液选择、支撑剂选择)。根据专家对各个指标的分析来确定各个因素的权重A=(05,03,02,0.4,0.3),并建立模糊关系矩阵(表1)。
采用Einstain算子(ε·,ε+)作为评价算子,由(1)~(9)计算出关于表1的模糊综合决策矩阵为B=(0.57,0.41,0.52,0.68,0.64),B(x4)最大。
据此得出影响到裂缝长度的原因主要是压裂液的选择问题。接下来便可针对压裂井的实际状况,提出下一步压裂改造施工应该调节压裂液的建议。
3.2 对比与分析
采用算子M(∧,∨),M(·,⊕),M(·,∨),M(·,+)进行压裂评价得到相应结果(表2)。
从表2中可以看到算子(∧,∨)的评价结果中B(x1)、B(x4)与B(x5)大小完全一样,则认为施工规模、压裂液的选择和支撑剂的选择起了相同的作用,显然据此无法作出有效地判断;算子(·,⊕)与(·,+)的模糊决策矩阵完全相同,所得的决策结果均是B(x4),体现不出各自的特性,文献1对此作了具体地分析;算子(·,∨)的决策结果也是B(x4),与Einstain算子(ε·,ε+)的结果一样。
根据非线性的Einstain算子(ε·,ε+)及其模糊综合评判模型,还可以将其运用到压裂井的选井以及压裂参数的分析应用中。实际应用表明,这种基于非线性算子的模糊综合评判方法比简单的“取大取小”模糊综合评判模型更有适用性,与实际结果更贴切。
4 结论
(1)模糊综合评判中有很多算子可用,选择合理有效的算子,做到优中选优十分重要,对模糊现象认识不足会错用算子使得应用结果不太理想。对于油气领域类似的模糊综合评判应用,仅简单地取用以Zadeh算子为基础的模糊评判模型会产生不确切甚至是错误的信息。实际中常对一个的模糊现象选用几种算子来处理,经过比较,才能达到预期效果。
(2)针对目前普遍使用的模糊评判方法,针对其产生失效性的,提出了基于Einstain算子的模糊综合评判模型。实际应用情况表明,改进的模糊综合评判模型和方法为压后改造分析和评价提供了合理的依据。
参考文献
[1] 谢庆宏.长沙嘉年华巴士有限公司绩效考评体系研究[D].合肥:合肥工业大学,2007.
[2] 张慧江.模糊综合评判在城市航测成图质量评定中的应用探讨[J].城市勘测,1995,(2):11-13.
[3] 肖明贵.桂林市岩溶塌陷形成机制与危险性预测[D].长春:吉林大学,2005.
[4] 何玉发,刘清友,朱永有,等.基于故障树的常减压装置模糊综合评判分析[J]. 石油化工设备,2007,(4):81-85.
[5] 王景波.基于平衡计分卡的煤炭企业绩效评价研究[D].青島:山东科技大学, 2008.
[6] 张鹏飞,郭大立,王东浩,等.压后综合评估的模糊方法研究[J]. 石油工业计算机应用,2008,(3):25-27.
[7] 贾楠.制造业信息化经济效益评价模型研究及应用[D]. 广州:华南理工大学, 2011.
[8] 王倩.模糊综合评判方法在风险分析中的应用[J]. 现代商贸工业,2014,(19):25-28.
[9] 张鹏,陆瑶,赵雨旸.基于模糊综合评价法的公路客运满意度研究[J]. 交通科技与经济,2014,(3):27-30.
[10]郭建春.压裂酸化选井的人工神经网络软件研制[J]. 天然气工业,2004,(11):97-99.
[11]崔丽娟.雄县电网扩建改造项目社会经济效益评价研究[D].北京:华北电力大学,2013.
