基于集中损耗的光伏发电单元年发电量RT-LAB仿真分析

奚霁仲, 李 飞, 张 兴, 马铭遥, 吴 凡, 陈 武

(1. 合肥工业大学电气与自动化工程学院, 安徽省合肥市 230000; 2. 国网安徽省电力有限公司广德县供电公司, 安徽省宣城市 242000)

0 引言

太阳能资源的开发利用是所有可再生能源中投资增长速度最快的,其中太阳能光伏发电是太阳能资源利用的主要方式之一,而发电量是定量评估光伏发电单元效益的重要指标。现有的对光伏发电单元的优化常以实现特定条件下的效率提高为目标,在全年复杂多变的环境下是否可以增加发电量仍然未知,因此对光伏发电单元发电量进行仿真具有重要意义。

大部分太阳能光伏发电量预报主要是通过太阳总辐射的准确预报,结合光伏电站历史发电量数据分析,进而得到光伏发电量预报[1]。文献[2]找到并改进了一种适用于新加坡气候条件的辐射估计模型,但没有对后续光伏发电系统进行研究。文献[3-4]利用神经网络法或多元线性回归法,通过气象数据和往年发电量计算得到光伏发电系统的发电量。这种计算方式将逆变器效率和线缆的损耗作为定值进行考虑,没有考虑逆变器参数和控制策略等因素对发电量造成的影响。因此，需要搭建可以反映光伏发电单元电力电子特性的详细模型。文献[5]利用受控源法来模拟并网光伏发电单元的逆变器电能转换和传输系统特性,也可以考虑部分参数对发电量的影响,但模型中并网光伏发电单元的输出电流只含有基波分量,不够精确。文献[6-7]按各元件的连接顺序,对光伏发电单元各部分进行仿真,真实反映了逆变器的控制特性和参数对发电量的影响,但没有对逆变器开关损耗和线路损耗进行仿真。文献[8-9]利用开关器件制造厂商提供的损耗相关参数,对逆变器损耗进行了计算。该方法准确有效,但所需参数较多,且对模型的仿真精度要求较高,仿真速度慢且运行时间长,对年发电量进行仿真缺乏可行性。

本文以某地实际光伏发电单元为原型,首先建立了光伏阵列及逆变器控制系统模型。其次对逆变器各部分损耗都进行了准确建模,提出在公共耦合点并联一个理想电流源模拟光伏逆变器损耗的建模方法,在不增加模型计算负担的情况下对损耗进行了精确建模。其后,通过对最大功率点跟踪(maximum power point tracking,MPPT)过程进行化简,大大缩减了年发电量仿真的运行时间。最后通过RT-LAB实时仿真平台搭建了本文所提出的光伏发电单元年发电量详细仿真模型,将仿真结果与实际系统的年发电量进行对比,验证了该模型的正确性,并分析不同逆变器效率曲线和控制算法对发电量的影响,为逆变器的选型提供了一定的理论指导。

1 并网光伏发电单元的建模

搭建并网光伏发电单元的详细模型是对发电量进行准确仿真的前提,其主要结构由光伏阵列、逆变装置和滤波器等组成。

1.1 太阳能光伏阵列模型

光伏电池是利用光伏效应把光能转变成电能的器件,其伏安特性随外界环境如光照强度和光伏电池表面温度的变化而变化,呈非线性特性。此时可以用函数来描述光伏电池输出电流[10]。

已知光伏电池短路电流Isc、光伏电池开路电压Voc、光伏电池最大功率点电流Im和光伏电池最大功率点电压Vm这4个参数后,光伏电池的数学模型可以表示为:

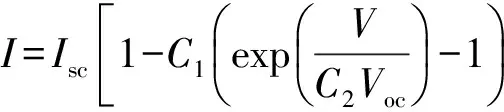
(1)

其中

(2)

(3)

在不同的电池温度和光照强度下,Isc,Im,Voc,Vm会按照一定规律变化。通过引入相应的补偿系数,近似推算出任意光照S和电池温度T下4个技术参数为:

(4)

(5)

Voc=Vocrefln(e+bΔS)(1-cΔT)

(6)

Vm=Vmrefln(e+bΔS)(1-cΔT)

(7)

式中:Iscref,Imcref,Vmref,Vocref为光伏电池在参考温度Tref=25 ℃下的技术参数;ΔT为气温变化量,ΔT=T-Tref;Sref为光照强度给定值;ΔS为光照强度变化量,ΔS=S/Sref-1;系数a,b,c的典型取值分别为0.002 5/℃,0.5,0.002 88/℃。

1.2 控制模型

并网光伏控制系统一般由MPPT控制及电压电流双闭环控制组成[11]。

MPPT的作用是根据温度、光照情况的变化,随时跟踪光伏电池最大输出功率点。目前常用的MPPT方法有恒定电压法、扰动观测法、电导增量法和最优梯度法等多种。由于扰动观测法实现容易、运行稳定,本文采用扰动观测法实现MPPT。

假设光伏电池的P-U特性曲线只存在一个极值,扰动观测法就是在光伏电池的起始工作点开始,每隔一段时间对光伏电池的工作电压进行一次扰动。若调整端口电压后光伏电池的输出功率增加,即说明此前的扰动能够提高光伏电池的输出功率,下一次计算应继续往相同方向变化光伏电池的输出电压;反之下一次扰动方向相反。在外部环境不变的情况下,MPPT输出电压给定值会在最大功率点附近波动。

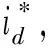
2 损耗模型的建立

对损耗模型的精确建模是建立光伏发电单元发电量模型的基础,但使用气象资料分析计算得到的发电量忽略了MPPT或逆变器控制算法和参数带来的影响,而受到模型复杂性的制约无法搭建详细模型对年发电量进行仿真。现有的发电量模型大部分没有详细考虑逆变器损耗和线缆损耗对发电量的影响。

2.1 并网光伏发电单元损耗分析

并网光伏发电单元的效率如附录A图A1所示[8]。主要损耗有MPPT损耗、直流线缆损耗、逆变器损耗、交流线路损耗和逆变器损耗等。

假设只考虑MPPT算法的单峰值特性,其损耗分为两种:一种是动态损耗,即温度和光照发生改变时,MPPT存在一个寻找最大功率的过程,需要一定的时间才能跟踪到最大功率点;另一种是稳态损耗,即使外部环境没有发生变化,MPPT也会使电压在最大功率点附近波动,由于没有完全跟踪而造成的损耗。增大电压步长或减小扰动时间可以更快地跟踪到最大功率点以减小MPPT的动态损耗,但同时也会增大稳态损耗或导致系统不稳。因此,合理选择MPPT控制算法和控制参数可以有效减小MPPT损耗。

当电流较大时,线缆的损耗不可避免。线缆的长度和阻值会影响线缆的损耗,交流侧的邻近效应和集肤效应也会额外增加线缆的损耗。

逆变器的损耗可以分为硬件损耗和软件损耗。硬件损耗包括开关损耗、滤波器损耗和直流侧电容损耗等;软件损耗包括控制策略带来的损耗,如MPPT电压步长、MPPT时间步长、逆变器电流环参数等都会影响逆变器损耗。

由于集中式逆变器到变压器的线路较短,所以交流部分的损耗主要为变压器损耗。变压器损耗主要分为铜损和铁损:铜损是指变压器一、二次电流流过该线圈电阻所消耗能量之和;铁损是指变压器在额定电压下(二次开路),在铁芯中消耗的功率,其中包括磁滞损耗与涡流损耗。变压器的效率还与负载有关,同一台变压器在不同负载下的效率也不同,一般在40%～60%额定负载时效率最高,轻载时效率很低,大容量变压器在额定负载时效率可达98%～99%。

造成光伏发电单元损耗的原因较多,即使硬件参数完全相同,不同的控制算法下其损耗也会有所差异,因此需要建立详细的损耗模型才能对发电量进行详细建模。

2.2 损耗建模策略

2.2.1逆变器损耗建模

逆变器的损耗可以分为软件损耗和硬件损耗。软件损耗包括控制策略带来的损耗,本文通过对逆变器的准确建模来仿真软件损耗,逆变器的控制参数(如MPPT电压步长、时间步长、逆变器电流环参数、电压前馈等)与实际光伏发电单元保持一致。

如图1所示,逆变器硬件损耗包括开关损耗、滤波器损耗和直流侧电容损耗等。图中:L1为逆变器侧电感;L2为电网侧电感;Rd为阻尼电阻;Cf为滤波电容。由于逆变器的输出电压,即电网电压基本不变,其输出功率主要由输出电流决定,所以本文提出在公共耦合点处并联一个受控电流源来代替光伏并网的功率损耗,通过调节受控电流源的幅值大小,来模拟逆变器在不同功率点处的损耗。由于逆变器工作在不同功率点时硬件损耗有所不同,本文通过调用离线测量的真实逆变器的效率曲线对模型中逆变器的损耗进行修正。

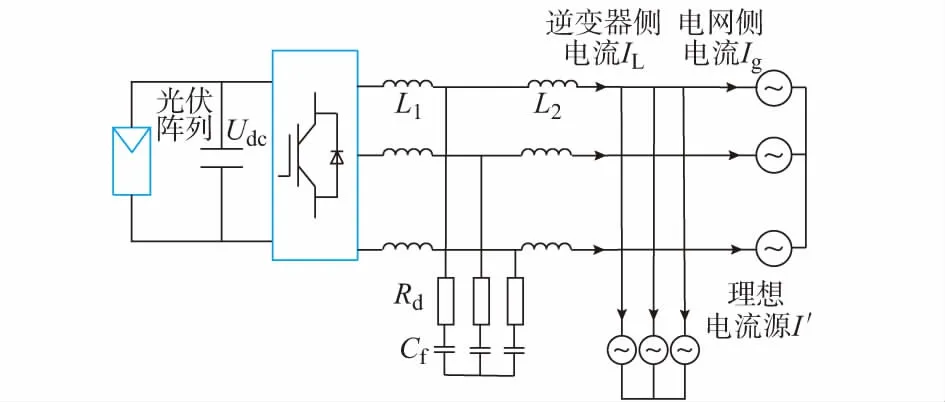
图1 损耗建模策略Fig.1 Strategy for power loss modeling

集中损耗模型具体搭建步骤如图2所示。

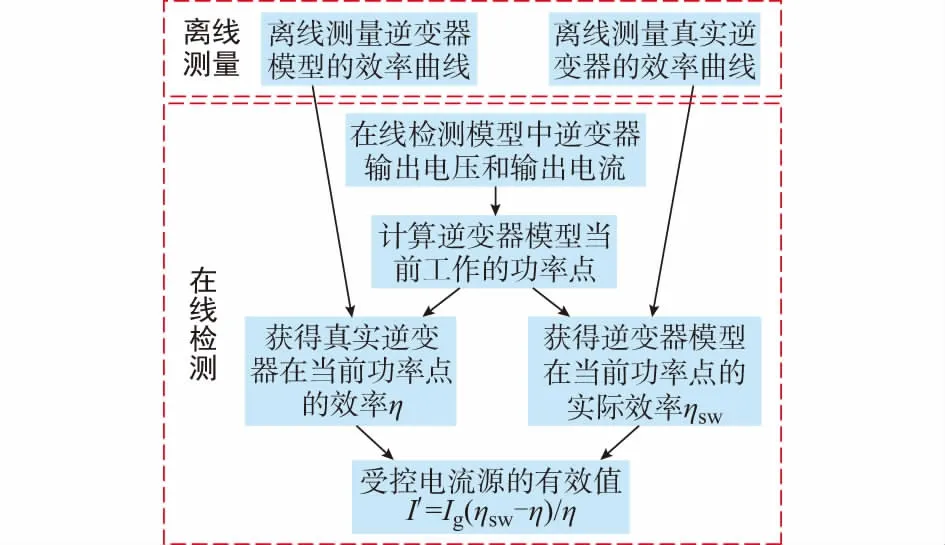
图2 集中损耗模型流程Fig.2 Flow chart of centralized loss model

步骤1:离线测量获得逆变器仿真模型的效率曲线。

步骤2:离线测量获得真实逆变器的效率曲线。

步骤3:在线检测逆变器公共耦合点相电压Up和电网电流Ig,可以计算得到逆变器的瞬时功率,即逆变器当前工作的功率点。

步骤4:根据步骤1中逆变器仿真模型的效率曲线和步骤3中逆变器当前工作的功率点x,可查得此时逆变器仿真模型的效率ηsw。

步骤5:根据步骤2中真实逆变器的效率曲线和步骤3中逆变器当前工作的功率点x,可查得此时逆变器仿真模型的期望效率η。

步骤6:在逆变器模型的交流侧并联受控源模型来进行补偿,由于逆变器的输出电压,即电网电压基本不变,因此可以通过调节电流源的幅值控制受控电流源吸收或消耗功率的大小。逆变器模型的期望效率η除以当前功率点逆变器仿真模型的效率值ηsw,即为受控电流源前后的功率之比,如下式所示:

(8)

式中:PPV为逆变器的输出功率;Ig和Ug分别为网侧电流和网侧电压;IL为逆变器网侧电感的电流;I′为代替损耗的受控电流源输出电流。

由此便得到了逆变器网侧电流Ig和受控电流源输出电流I′的对应关系式:

(9)

通过实时检测逆变器网侧电流Ig,便可以计算得到受控电流源输出电流I′来代替逆变器整体的损耗。

该方法只需要真实逆变器的效率曲线,不需要绝缘栅双极型晶体管(IGBT)等详细参数,而且考虑了逆变器工作方式、控制参数等对损耗的影响,可以在不显著增加模型计算负担的条件下,对逆变器损耗进行精确建模。

2.2.2其他损耗建模

根据光伏电站的结构特点,直流线损可分为光伏组件到汇流箱、汇流箱到逆变器两个部分,在模型中将上述两部分直流线缆等效为两个电阻。本文将光伏组件中所有的光伏电池板等效为一块,假设所有线缆长度相等,则光伏直流线缆等效电阻值可由下式进行计算:

(10)

式中:ρ为导线的电阻率;l为所有导线总长度;n为并联导线数,光伏电站的两段直流线缆的导线并联数分别为汇流箱的总接入路数和汇流箱个数。

对于不超过100 km的电缆线路来说,可以不考虑其分布参数特性,只需将线路参数简单地集中起来的电路来表示。等值电路有π形等值电路和T形等值电路,本文使用常用的π形等值电路。由于考虑到临近效应和集肤效应等,交流电阻的实际阻值会比直流电阻值要大,如下式所示:

Rac=KjfKijRdc

(11)

(12)

(13)

式中:Rac为交流电阻值;Kjf为集肤效应系数,当频率为50 Hz,芯线截面不超过240 mm2时,Kjf均为1;Kij为临近效应系数;r为线芯半径;δ为电流透入深度,因集肤效应使电流密度沿导线横截面的径向按指数函数规律分布,可以近似等效为电流仅在导线表面厚度中均匀分布;μ为相对导磁率,对于有色金属导线为1;f为电流频率。

变压器的损耗主要分为铜损和铁损。额定电流流过变压器时,高低压绕组中的总铜耗近似等于变压器短路损耗Pk,大容量变压器的阻抗中以电抗为主,即变压器的电抗和阻抗数值上接近相等,因此变压器高低压绕组的总电阻和总电抗可由式(14)和式(15)计算得到。变压器的铁耗近似与空载损耗P0相等,因此变压器励磁绕组的电导和电纳可由式(16)和式(17)计算得到。

(14)

(15)

(16)

(17)

式中:RT为变压器高低压绕组的总电阻;SN为变压器额定容量;UN为变压器额定电压;XT为变压器高低压绕组的总电抗;Uk为变压器的短路电压百分比;GT为变压器的电导;BT为变压器的电纳;I0为电压器的空载电流百分值。

3 年发电量仿真分析

年发电量仿真的最大难点是影响因素多、仿真时间长,以及如何有效去除对发电量影响较小的因素。多数论文都忽略了逆变器参数和控制算法对发电量的影响,然而厂家可以通过人为选择逆变器参数和型号来提升发电量,因此选择忽略逆变器参数和控制算法对发电量的影响具有一定的局限性。本文搭建了详细模型,只通过对MPPT过程的化简来缩短模型运行时间。

由于外部环境一般缓慢变化,所以年气象数据一般以小时为单位。本文近似使用每小时的平均光照强度和温度作为输入,一年近9 000个数据以Excel表格的形式导入Signal Builder模块中作为输入。从气象台获取的数据为气温,需要转化为光伏组件的温度,根据文献[12]得到气温到光伏电池板温度的近似关系式为:

y=T+0.0214xr+6.12

(18)

式中:y为光伏组件的温度;T为气温;xr为太阳辐射度。

不断改变光照和温度,MPPT输出直流电压指令值如附录B图B1所示。可以看到MPPT在跟踪到最大功率点后会在附近来回波动,4步为一个周期,而且当外部环境发生变化后,MPPT输出电压指令值在0.8 s内均可以达到稳态。由于逆变器MPPT速度较快,外部温度和光照强度变化较慢,因此可以认为逆变器一直在最大功率点附近工作,MPPT的损耗主要由稳态损耗构成。

基于上述原因,本文设定1 h的数据在RT-LAB中运行1 s,用逆变器跟踪到最大功率点后一个MPPT周期的平均功率来代替这1 h的平均功率,对该周期的功率进行积分再乘以比例系数3 600/0.2=18 000,即得到这1 h光伏发电系统的发电量。

4 仿真验证及结果分析

为验证本文提出的损耗建模和发电量仿真方法的准确性,本节以国内某地区光伏发电单元实测数据与该模型输出进行对比分析,以验证该模型是否准确。

4.1 仿真模型搭建

本文以某地区实际光伏发电单元为原型搭建了年发电量仿真模型,具体参数如附录C表C1、表C2所示。此光伏发电单元共有14台汇流箱,每台汇流箱的实际接入线路数如表C3所示,根据式(10)计算可得光伏组件到汇流箱的导线并联数为198,等效电阻值为1.36 mΩ,汇流箱到逆变器的导线并联数为14,等效电阻值为2.21 mΩ。根据表C2和式(11)至式(13),计算可得逆变器到箱变的交流电缆阻值为4.51 mΩ。根据表C1中变压器的参数和式(14)至式(17),计算可得变压器高低压绕组的总电阻为6.05 Ω,总电抗为79.625 Ω,变压器励磁支路的电导为1.46×10-8S,电纳为1.41×10-8S。

即使在不增加模型计算负担的情况下,使用损耗集中方法对损耗进行了准确仿真,对MPPT过程进行化简也极大地缩短了仿真运行时间,年发电量仿真模型仍需运行365×12=4 380 s。在使用Simulink运行年发电量模型时仍出现了闪退,并且提示超出内存的错误,因此使用RT-LAB软件对年发电量进行仿真。

RT-LAB软件是一款由加拿大Opal-RT公司开发的基于系统信号应用和模型设计的仿真软件包,可以将MATLAB建立的仿真模型在RT-LAB实时仿真平台上运行。RT-LAB使用ARTEMIS实时解算算法,将稳态情况下指定的网络拓扑存储于内存中,如果系统运行过程中出现己存储的拓扑,可直接从内存中读取,节省了很多重新计算的时间,从而计算速度更快、结果更精确,使得基于模型的实时运行成为可能。将Simulink模型转换为RT-LAB实时仿真模型,需要完成如下步骤。

步骤1:划分子系统。为满足分布式要求必须对数学模型进行重新划分,将主电路和控制部分放入sm_子系统,将用户监控部分放入sc_子系统。

步骤2:插入OpComm通信模块。RT-LAB中的控制台子系统和其他子系统的数据交换通过以太网传输,为异步运行,主运算子系统和从运算子系统的数据交换通过火线传输,为同步运行。RT-LAB中的子系统是在接收到所有的信号之后才开始计算,因此进入子系统的输入信号需经过OpComm通信模块进行匹配。OpComm模块为RT-LAB提供从一个子系统到另一个子系统所发送的信号类型、大小等信息。

步骤3:系统连接与调试。实现模型分割后,首先在离线状态下对RT-LAB模型进行调试,调试无错后打开RT-LAB主控制界面,按步骤完成模型的编辑、C代码编译、代码生成等步骤,再转换为可在实时仿真计算机上运行的实时代码,最后进行加载,实现系统的运行和显示。

4.2 损耗模型仿真验证

使用受控电流源模拟损耗的RT-LAB仿真结果与有效实测数据的对比情况如表1所示。通过分析可知:模型和实测的逆变器效率曲线相比,最大的误差不超过0.02%,本文所提出的损耗建模策略可以模拟真实逆变器各组件带来的损耗。

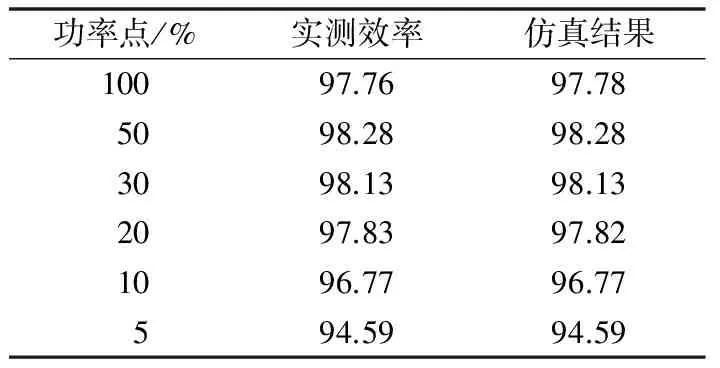
表1 仿真与实测的逆变器效率对比Table 1 Comparison of simulated and measured inverter efficiencies

该方法不需要详细的逆变器参数即可在模型中在线模拟逆变器的损耗,增加了逆变器模型的准确性,而且方法简便,不会对逆变器模型造成新的计算压力。

在额定温度的条件下,改变光照强度使光伏发电单元工作在不同的功率点,光伏发电单元各部分损耗如表2所示,数据基本符合调研得到的电站损耗分布。其中逆变器和变压器的损耗在50%功率点处最小,在低载荷情况下损耗较大;直流线缆的损耗主要和线路电压有关,所以随着输出功率的降低,损耗也逐渐降低;MPPT跟踪造成的损耗较小,和工作的功率点无关。

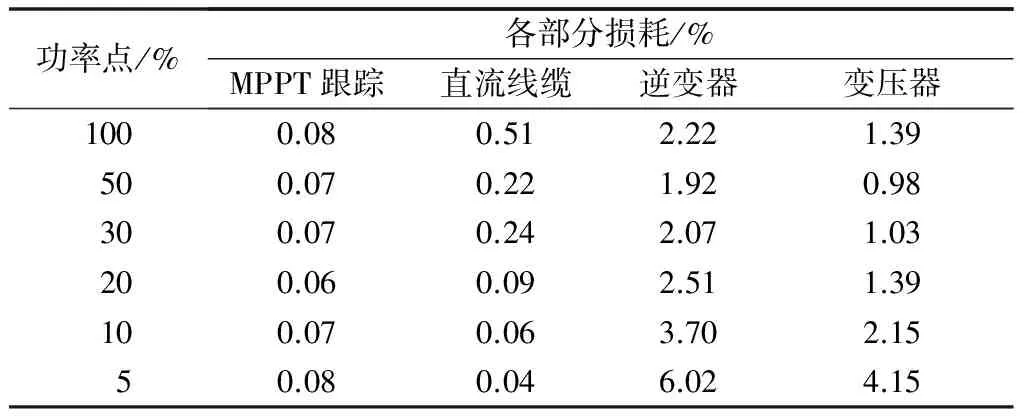
表2 光伏发电单元各部分损耗Table 2 Power loss of grid-connected photovoltaic unit

4.3 年发电量仿真验证

基于对光伏发电单元的详细建模,根据实测的环境气象数据对该地区某光伏发电单元年发电量进行仿真,并网光伏发电单元的直流侧、逆变器和变压器的年输出电量如图3所示。仿真模型中,光伏发电单元年发电量为600.111 MW·h,与其实际发电量599.001 MW·h相比,误差仅为0.17%。

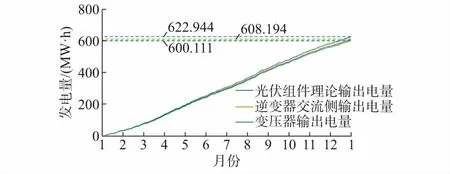
图3 光伏发电单元各部分输出电量Fig.3 Output power of each part of photovoltaic unit

本文的算法是对每个小时的发电量计算过程进行化简,得到光伏发电单元每个小时的输出电量后不断重复此过程。因此,年发电量已重复该算法超过4 000次,结果的准确性并不具备偶然性。比较全年的光伏发电单元实际输出功率和仿真模型输出功率,最大误差小于0.2%,满足光伏发电单元建模仿真要求。限于篇幅,本文在附录B表B1中,任意选取某天中该光伏发电单元实际输出功率和仿真结果进行对比。

具体分析图3可知,光伏组件理论年输出电量为622.944 MW·h,逆变器交流侧年输出电量为608.194 MW·h,变压器年输出电量为600.111 MW·h,在包括MPPT和滤波器损耗的情况下,逆变器和变压器的损耗所占比重仍然很小,分别仅占全年发电量的2.34%和1.35%,因此通过降低逆变器和变压器损耗来提升发电量的空间并不大。很多人主观认为夏季辐照强,因此发电效率更高,比较图中逆变器输出电量曲线在不同时间的斜率可知,光伏发电单元在春秋季天气晴朗且温度凉爽时发电效率最高。这是由于发电量受到光照强度和光伏组件板温的影响,二者既相互制约,又共同发挥作用,总体表现出双向变化趋势,即辐射量正向变化、板温负向变化。

最大转换效率只能片面地评价逆变器的发电效率,而实际光伏发电单元中发电量是逆变器选取的主要衡量标准。不同的控制方法或者逆变器型号会影响到逆变器的效率曲线,对于逆变器来说即使各参数相同,供应商不同所实测的逆变器效率曲线也不完全相同。附录B图B2为4种供应商不同的逆变器效率对比。

实际工作中,逆变器的效率和工作的功率点有关,即随光照强度和温度的变化而变化,不会一直工作在最大转换效率处。欧洲效率是根据欧洲光照条件,给出一个有标准配置阵列的光伏逆变器在不同功率点的权值,但中国太阳能资源条件与欧美相差较大,欧洲效率并不适用于中国的使用要求,而且由于中国地域辽阔,各地的光照强度和温度也不完全相同。搭建并网光伏发电单元详细模型之后,可以根据当地经典年光照和温度仿真得到光伏发电单元在各功率点的发电量分布,如附录B图B3所示。可知光伏发电单元在功率点60%附近所发电量最多,因此厂家在进行逆变器选型时也应重点关注此功率点的逆变器转换效率而非最大转换效率。

除了定性判断发电量分布,本文对这4种逆变器分别进行了年发电量仿真,逆变器1至4的年发电量分别为600.0,600.4,600.6,599.5 MW·h。可以看出,使用逆变器3的光伏发电单元年发电量最多,相比于使用逆变器4的发电量提升了0.15%。

5 结语

本文以某大型光伏发电单元为原型,使用RT-LAB实时仿真平台搭建了光伏发电单元详细模型。通过MPPT过程的化简,大大缩减了模型运行时间,同时在公共耦合点并联了一个受控电流源来代替逆变器硬件损耗,使模型更加准确且基本不会增加计算负担。本文以实际的气象资料为输入,对某地实际光伏发电单元进行年发电量仿真,由于考虑了逆变器控制算法和参数的影响,该仿真模型更加准确,仿真结果与实际数据最大误差不超过0.2%。该模型通过分析不同逆变器效率曲线和控制参数对年发电量的影响,以指导厂家进行选型。

实际光伏电站发电量的影响因素较为复杂,除MPPT损耗、逆变器损耗、线路损耗和变压器损耗外,光伏阵列的损耗也不容忽视。在后期的研究工作中,需要对阴影遮挡、热斑、光伏电池板参数等因素对发电量的影响进行建模,使年发电量的仿真更加准确。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 李芬,陈正洪,成驰,等.太阳能光伏发电量预报方法的发展[J].气候变化研究进展,2011,7(2):136-142.

LI Fen, CHEN Zhenghong, CHENG Chi, et al. Review on forecast methods for photovoltaic power generation[J]. Advances in Climate Change Research, 2011, 7(2): 136-142.

[2] LIN P N, SRINIVASAN D. Estimation of solar power generating capacity[C]// IEEE International Conference on Probabilistic Methods Applied to Power Systems, June 14-17, 2010: 95-100.

[3] 代倩,段善旭,蔡涛,等.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究[J].中国电机工程学报,2011,31(34):28-35.

DAI Qian, DUAN Shanxu, CAI Tao, et al. Short-term PV generation system forecasting model without irradiation based on weather type clustering[J]. Proceedings of the CSEE, 2011, 31(34): 28-35.

[4] 蒋浩,洪丽,张国江.主成分分析结合神经网络的光伏发电量预测[J].电力系统及其自动化学报,2013,25(6):101-105.

JIANG Hao, HONG Li, ZHANG Guojiang. PV generation system forecasting model based on neutral network and principal components analysis[J]. Proceedings of the CSU-EPSA, 2013, 25(6): 101-105.

[5] 李晶,许洪华,赵海翔,等.并网光伏电站动态建模及仿真分析[J].电力系统自动化,2008,32(24):83-87.

LI Jing, XU Honghua, ZHAO Haixiang, et al. Dynamic modeling and simulation analysis of grid PV power station[J]. Automation of Electric Power Systems, 2008, 32(24): 83-87.

[6] KI K S, HONG J J, HEE C C, et al. Modeling and simulation of a grid-connected PV generation system for electromagnetic transient analysis[J]. Solar Energy, 2009, 83(5): 664-678.

[7] WANG L,LIN Y H. Dynamic stability analyses of a photovoltaic array connected to a large utility grid[C]// Proceedings of IEEE Power Engineering Society Winter Meeting, January 23-27, 2000, Singapore: 476-480.

[8] 黄伟煌,胡书举,许洪华.中点钳位型中压三电平风电变流器的损耗分析[J].电力系统自动化,2014,38(15):65-70.DOI:10.7500/AEPS20130902008.

HUANG Weihuang, HU Shuju, XU Honghua. Power loss analysis of NPC medium-voltage three-level converters for wind power generation system[J]. Automation of Electric Power Systems, 2014, 38(15): 65-70. DOI: 10.7500/AEPS20130902008.

[9] 王海田,汤广福,贺之渊,等.模块化多电平换流器的损耗计算[J].电力系统自动化,2015,39(2):112-118.DOI:10.7500/AEPS20130706002.

WANG Haitian, TANG Guangfu, HE Zhiyuan, et al. Power losses calculation of modular multilevel converter[J]. Automation of Electric Power Systems, 2015, 39(2): 112-118. DOI: 10.7500/AEPS20130706002.

[10] 杨永恒,周克亮.光伏电池建模及MPPT控制策略[J].电工技术学报,2011,26(增刊1):229-234.

YANG Yongheng, ZHOU Keliang. Modeling of photo-voltaic cell and MPPT control strategy[J]. Transactions of China Electrotechnical Society, 2011, 26(Supplement 1): 229-234.

[11] 张兴,曹仁贤.太阳能光伏并网发电及其逆变控制[M].北京:机械工业出版社,2010.

[12] 程序,谭志萍.一种光伏电池组件的温度预测方法[J].物联网技术,2013(11):32-33.

CHENG Xu, TAN Zhiping. A temperature prediction method for PV cell module[J]. Internet of Things Technologies, 2013(11): 32-33.