计及用户行为的需求响应对分布式发电系统充裕度的影响
2018-04-24隆竹寒王昊婧顾姗姗
武 赓, 隆竹寒, 曾 博, 曾 鸣, 王昊婧, 顾姗姗
(1. 新能源电力系统国家重点实验室(华北电力大学), 北京市102206; 2. 北京电力经济技术研究院, 北京市 100055; 3. 国网(北京)节能设计研究院有限公司, 北京市 100052)
0 引言
随着可再生能源渗透率的不断提高,需求响应(demand response,DR)逐渐成为电力系统中重要的可控资源,对DR资源进行调控能够有效提高未来新能源电力系统运行的经济性和可靠性[1]。研究DR对系统发电充裕度以及可靠性的影响对于定量分析DR实施效益,以及未来DR参与现货以及容量电力市场交易都具有十分重要的意义[2]。
当前,国内外针对DR对于系统发电充裕度的影响已经进行了一些研究。文献[3]分析了在实施需求侧管理后,负荷变化对于系统发电充裕度的影响;文献[4]提出了一种DR资源对发电充裕度影响分析的评估流程,说明了DR资源能够有效提高系统的可靠性,同时响应节点用户的负荷反弹特性能够影响DR对于系统发电充裕度的贡献程度;文献[5]通过马尔可夫模型将DR资源等效为传统机组,分析了DR资源的不确定性对系统可靠性的影响以及DR自身的可靠性效益;文献[6]则重点分析了DR资源对配电网可靠性的影响。
上述研究多数只是基于负荷本身的物理特性或者DR技术潜力进行建模分析。而在电力市场环境下,用户是否愿意参加DR项目往往取决于其参与DR项目的收益和对其用电行为的影响。因此,用户对于参与行为的选择是影响系统中DR可用程度的重要因素[7]。当前,已有文献对于DR资源不确定性的研究基本都是在系统运行问题中,文献[8-9]都是通过在用户负荷弹性上添加纯随机扰动参数来描述可用DR资源以及用户行为的不确定性;文献[10]是通过构建涵盖具有均匀分布不确定性参数的用户效用折损函数来对用户DR行为选择波动进行描述。综上所述,当前对于DR资源可用量以及用户行为的建模都比较简单,尤其是在系统充裕度分析中很少考虑用户选择行为的影响。
鉴于此,本文基于后悔度匹配机制构建了计及用户行为选择的DR资源时序动态分析模型,提出了基于序贯蒙特卡洛方法的DR资源对分布式发电系统(distributed generation system,DGS)发电充裕度的影响评估流程。通过算例仿真,分析了DR对分布式发电系统发电充裕度的影响,以及节点负荷特性尤其是用户行为选择对DR可靠性贡献程度的影响。
1 分布式发电系统中电源的可靠性模型
在分布式发电系统中,可用电源主要包括传统能源分布式电源(如燃气机组),可再生能源分布式电源以及主网变压器[11]。在本文中为简化模型,传统能源分布式电源只考虑分布式燃气机组,可再生能源分布式电源只考虑分布式风机,本文所提的分布式电源评估流程对于其他形式的分布式电源均具有适用性。
1.1 分布式电源可靠性模型
对于传统的燃气机组,在不考虑其燃料供应问题的条件下,其在某一时刻的可用容量由其是否处在正常工作状态决定[12]。因此,可以基于其故障率和维修率参数,构建两阶段的马尔可夫模型,从而确定燃气机组的时序状态序列和可用容量序列[12]。
对于分布式风机,其出力受风速大小影响。因此,需要先构建风速不确定性模型,再根据风速—出力关系函数确定其时序可用容量序列[13]。本文基于中国西北某地区的风速数据,通过ARMA(p,q)模型描述其风速的时序特性[12],如式(1)—式(3)所示。
(1)
vt=φt+σtyt
(2)
(3)

1.2 主网变压器可靠性模型
由于主网电源向分布式发电系统供电能力受主网电源可用容量的影响,因此,在分布式发电系统发电充裕度分析中需要对主网变压器的出力不确定性进行等效的定量描述。在本文中,假设主网变压器的可用容量波动概率服从均匀分布[11],其出力可表示为:
(4)

2 DR模型
在系统层面,用户的DR潜力不仅由其用电器自身的负荷物理特性决定,其参与行为的选择同样是影响不同时段系统中DR可用程度的重要因素。鉴于此,本文将从用户负荷特性和行为选择两个方面,构建适用于分布式发电系统发电充裕度评估的DR分析模型。本文假设用户所参与的DR项目为激励型DR项目[2]。
2.1 用户负荷建模
根据用户用电器的用电物理特性以及用电优先级,一般用户的用电负荷可分为刚性负荷、可中断负荷和可转移负荷[14]。
1)刚性负荷
刚性负荷一般是指用户不具备DR能力的负荷,用户对这类负荷的需求是近似刚性的,例如居民用户的电冰箱以及商业和工业用户基本的照明和生产负荷,因此该类负荷可表示为:
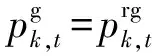
(5)
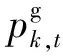
2)可中断负荷
可中断负荷是指用户可部分或全部中断的用电负荷,例如洗衣机和洗碗机,其负荷特性可表示为:
(6)
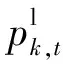
3)可转移负荷
可转移负荷是指在优化周期内其各个时段用电模式可以灵活调整的负荷,例如电动汽车。本文中假设该类型负荷在其工作周期内总的电量消耗是固定的,系统可以根据需要对其各个时段的用电负荷进行优化,其负荷特性可表示为:
(7)
(8)

(9)


2.2 用户行为意愿模型
对于用户来说,是否参与DR以及参与程度取决于用户对于参与DR项目后的期望收益,以及参与DR后对自身用电行为影响所造成的效益折损。实际上,当用户在参与激励型的DR项目时,电网公司或者系统运营商需要相关用户事先上报在此次合同周期或者当前DR事件中的参与程度或者参与量,从而为系统调控提供相应的参考依据。但是用户在上报相关信息时,并不能确定在当前事件中DR实际参与效益(因为无法确定此次DR的实际调用量),也无法知道其余用户的参与策略以及其参与DR项目所获得的实际收益。在这样的信息条件下,用户只能够通过自身以往参与DR所获收益以及对应的策略来选择此次DR的参与策略或者参与程度。
基于用户的上述行为选择特点,本文将基于改进“后悔度匹配机制”构建用户行为选择的概率模型[15]。改进“后悔度匹配机制”仍是基于传统后悔度匹配的学习机制,即事件参与者会根据过去所有相关事件发生结果的“后悔度测度”来选择下一阶段相关事件的参与策略[16]。其中,“后悔度测度”是事件参与者基于历史的策略选择和对应的实际效益,在其他因素不变的条件下,将过去所有已发生事件的实际参与策略j替换为新的参与策略i,计算如果历史上所有的相关事件均采用新的参与策略i后所得效益可能的增量[15]。基于上述原则,“后悔度测度”越大,事件参与者在下一阶段选择舍弃原有参与策略j,而使用新策略i的可能性就越大,并且选择新策略的可能性与所计算出的“后悔度测度”呈正相关关系[15]。本文中假设每次用户需要向系统运营商上报自身的DR的参与程度μk,数学表述形式将在下文具体阐述。
1)用户效益函数
对于激励型DR项目,用户参与DR效益一般由参与DR后的补偿以及参与后的效用折损的差值确定,可表示为:

(10)

用户参与DR的补偿和效益折损函数一般可表示为以下形式[17-18]:
(11)

(12)
(13)
(14)
式中:bl与bs分别为DR项目对于用户可中断负荷以及可转移负荷的补偿价格;Δt为用户k某次DR参与的时长;N为用户可转移负荷的调用次数;ak,t,ak,t′,mk,mk′为用户效用参数,对于不同用户取值不同,均为正数;T′为系统中出现负荷缺口的时间区间。在实际应用中,相关参数可根据用户实际的用电数据得出[19]。对于用户的效用函数,文献[17-18]有更进一步的讨论。
式(11)和式(13)分别表示可中断负荷和可转移负荷的补偿效益。本文中假设用户的DR收益与实际调用程度呈线性关系,即用户中断负荷补偿与中断负荷大小以及中断时长呈线性正相关关系;可转移负荷补偿只和其最大额定功率相关,式(13)是将可转移负荷补偿费用均摊到每次调用中。式(12)和式(14)分别表示可中断负荷和可转移负荷相应的效益折损。可中断负荷和可转移负荷的效益折损分别服从二次和指数函数,上述函数已经普遍应用于对用户用电效益或者用电舒适度折损的建模,具有一定的一般性。
2)改进后悔度匹配机制
本部分将基于改进后悔度匹配机制对用户DR参与意愿进行建模。本文中将用户参与DR的策略集离散化,即Πμ={μk|μk=0,0.1,0.2,…,1;∀k},假设μk的取值步长为0.1,取值范围为[0,1]。用户能够在接到系统发出的DR信号后,选择在此次DR事件中的实际参与程度。
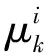
(15)
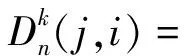
(16)

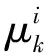

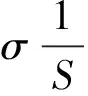
(17)
(18)

基于上述模型,用户在选择下一阶段的DR参与策略时,会基于自身历史参与DR项目实际的效用值和相应的策略做出判断。由此,通过式(5)—式(9)以及式(17)和式(18)可以得出用户在某个时间段内可调用的DR资源大小。
3 发电充裕度评估流程
分布式发电系统的发电充裕度的基本定义是分布式发电系统中实际可以满足负荷需求的发电资源[11]。在本文中,序贯蒙特卡洛算法将用于分析DR对于分布式发电系统发电充裕度的影响。因为用户的可响应负荷以及行为选择具有时序性,序贯蒙特卡洛方法能够更好地保留上述信息,从而更准确地分析DR对于系统发电充裕度的实际贡献[20]。具有评估流程如下。
步骤1:基于分布式发电系统中各元件的故障率和修复率参数,通过逆变换函数抽样确定分布式发电系统中分布式风机、分布式燃气机组、主网变压器的8 760 h的年状态序列[11],进而根据式(1)—式(4)确定上述元件的年出力时序序列。

(19)
(20)
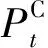
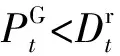
步骤4:基于当前各用户的DR参与意愿值,系统运营商对当前系统中的DR资源进行调控。系统运营商以系统停电成本最低为目标,在T=24的自然天内对系统中可用的DR资源进行调用,其调控模型如下:
(21)
约束条件如下:

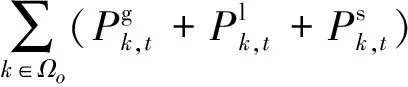
(22)

(23)
∀t∈T,(i,j)∈O
(24)

(25)
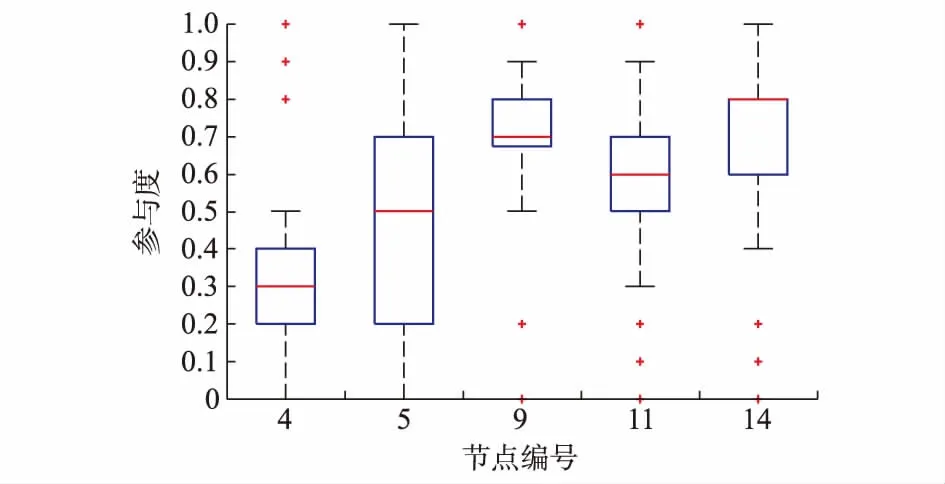
Vo,min (26) 0 (27) 步骤5:基于步骤4的结果,计算此次DR调用后的系统失负荷时长Yd以及未供应电量Zd[24]。具体表达式如下: (28) (29) 重复步骤3至步骤5,直到t=8 760,即遍历当前自然年中各小时的系统运行情况。 步骤6:重复步骤1至步骤5,当满足蒙特卡洛法的收敛要求时,计算分布式发电系统的可靠性指标,即电力不足时间期望和电量不足期望[24],本文分别用YLOLE和ZEENS表示,即 (30) (31) 式中:M为满足方差系数收敛要求时,采用蒙特卡洛法进行的仿真年数。 本文将基于国内西北地区某一分布式发电系统对上述模型进行仿真计算,该系统示意图如附录A图A1所示。该分布式发电系统通过一个220 kV变电站与主网相连,变电站额定变电容量为240 MVA;系统中2台25 MW的燃气机组在节点6处接入系统;节点8和节点15处共接入86 MW分布式风机。系统的最大负荷为290 MW,其中节点4,5,9,11,14为可响应负荷节点。系统中不同元件的可靠性参数以及风机和变压器出力参数见附录A表A1和表A2。 在本文中假设各可响应负荷节点处均为节点型用户,其各类型负荷的年负荷曲线是节点处单一用户负荷年负荷数据之和。节点4,5,9,11,14的各类型负荷的年负荷曲线以及相关负荷参数见附录A图A2和表A3。DR节点的激励价格参数为bl=1元/(kW·h),bs=5元/kW[25]。在本文中,在用电高峰(07:00—21:00)系统的平均停电成本设为12元/(kW·h),用电非高峰时为7元/(kW·h)。该分布式发电系统的初始可靠性指标为YLOLE=13.72 h/a,ZEENS=961.29(MW·h)/a。 为了分析DR对分布式发电系统发电充裕度的影响,本文中选取了电力不足时间期望YLOLE以及电量不足期望ZEENS作为系统发电充裕度的判断指标[24]。DR资源引入后可靠性指标变化如表1所示。 表1 DR资源引入后系统的可靠性指标Table 1 Reliability indices of system with DR resource 从表1中可以看出,当引入DR资源后,系统的可靠性指标均有所提高。为了更好地说明DR在提高系统发电充裕度上的作用,本文中选取蒙特卡洛仿真中系统某天的实际运行情况,对比DR调控前后系统中的负荷缺口,具体见附录A图A3。当天16:00系统中有一台分布式燃气轮机故障(由燃气机组状态抽样得到),且当天风速状况较差,使得系统中出现了负荷缺口。当天16:00—24:00系统持续缺电8 h,总缺电量为120.45 MW·h。当开始调用DR资源时,系统中的负荷缺口明显减少,缺电时长减少到5 h,总的缺电量减少到14.27 MW·h。由于可转移负荷的自身特性,在16:00调用DR资源后,系统之前的负荷需求有所增加;同时,当负荷缺口持续一段时间后,用户可转移负荷的可调用量减少,加之在20:00以后系统中可中断负荷可调用量也相应减少,所以在19:00后系统中仍然存在部分负荷缺口,具体见附录A图A3。 从表1中还可以看出,当DR容量增加,即按10%,20%,30%比例增加各节点可响应负荷大小时,系统可靠性也进一步提高,但是增长速度随DR容量增加逐渐减缓,说明DR对分布式发电系统发电充裕度的边际效益逐渐减小。 负荷自身的物理特性是影响DR资源可调控程度的重要因素。为了说明负荷特性对系统发电充裕度的影响,本部分设置了3个不同场景对上述问题进行分析。 情景1:所有可响应节点各个时段负荷值不变,用节点9的各类型负荷特性替代其他可响应节点原负荷特性。 情景2:所有可响应节点各个时段负荷值不变,用节点11的各类型负荷特性替代其他可响应节点原负荷特性。 情景3:所有可响应节点各个时段负荷值不变,用节点14的各类型负荷特性替代其他可响应节点原负荷特性。 参考情景为该分布式发电系统原始的发电充裕度,具体结果如表2所示。 表2 考虑不同负荷特性的分布式发电系统发电充裕度指标Table 2 Supply adequacy indices of distributed generation system considering different load characteristics 从表2的结果可以看出,虽然3个情景下,系统的发电充裕度都有所提高,但是在情景1条件下,系统的发电充裕度最高,情景3次之,情景2最差。上述结果说明节点本身的负荷特性能够影响DR对分布式发电系统发电充裕度的贡献程度。在各类型负荷中节点9的可中断负荷比例较高,节点11的可转移负荷比例较高,而节点14的可中断负荷和可转移负荷比例基本相同(详见附录A表A3和图A2),且3个节点的可响应DR潜力(可转移负荷和可中断负荷最大值之和)基本相同,对照表2中的结果可以得出,可中断负荷对于系统发电充裕度的贡献更大,而可转移负荷由于弹回效应,对系统充裕度的贡献不如可中断负荷。 本小节通过对比2个场景,分析用户行为选择对系统中DR的可用程度产生的影响。 情景A:不考虑用户的行为选择。基于本文中对于DR资源的建模,即在蒙特卡洛仿真中所有用户的参与度都为1。 情景B:考虑用户的行为选择,基于本文所提出的用户行为动态模型,在蒙特卡洛仿真中确定不同DR事件中的用户行为选择。 具体结果如表3所示。 表3 用户行为对分布式发电系统发电充裕度的影响Table 3 Influence of user’s behavior on supply adequacy of distributed generation system 从表3的结果中可以看出,情景A中YLOLE和ZEENS分别比情景B中减少了30.38%和4.52%,说明若不考虑用户行为选择的动态过程和波动性,会过高地估计DR资源对系统可靠性的贡献程度。 图1为蒙特卡洛仿真过程中的各个响应节点的年平均响应电量,可以发现当考虑了用户行为选择特性后,所有节点的响应电量均有所减少,但是节点4和节点9的响应电量变化不大,节点5的变化最明显。结合图2中各响应节点参与程度箱线图,可以看出当考虑用户行为的动态波动过程后,不同节点的DR参与程度波动范围不同。节点4的DR参与度一直较低,基本在[0.2,0.4]的范围内,节点9的DR参与度一直较高,基本在[0.7,0.8]范围内。节点4和节点9参与度的波动程度都较小,而节点5的参与度波动程度较大,说明节点5用户的行为随机波动性更强,而这种行为的波动性能够较大程度上影响响应节点实际的响应潜力。 图1 蒙特卡洛仿真中不同节点的年平均响应电量Fig.1 Average annual DR quantity at different nodes in Monte Carlo simulation 图2 蒙特卡洛仿真中各可响应节点参与度的箱线图Fig.2 Boxplot of participation rate at DR node in Monte Carlo simulation 如2.2节中所述,基于改进后悔度匹配机制的用户行为模型,能够反映出用户随机的行为波动以及波动程度,惯性系数λ的取值不同,用户行为维持原有参与策略的惯性程度也不同,λ较小,用户在不同策略之间切换的概率较小;λ较大,用户的行为则具有更强的波动性。在实际应用中,工业用户和部分商业用户具有较大容量的可中断负荷以及比较平稳的可响应负荷(如节点9),或者关键负荷用户,可响应负荷容量有限(如节点4),其DR参与程度往往比较稳定,而居民用户的可响应负荷往往波动较大(如节点5),用电行为选择也具有更多的主观性,使得其DR参与程度具有更强的波动性,因此,可以根据实际的数据调研,更为准确地确定和调整其λ值。式(17)中σ/S为随机波动项,能够保证每个策略均有最小的被选择概率,从而反映用户在行为选择中所表现出的主观纯随机性。基于上述对用户行为选择的定量分析,能够更准确地评估DR对系统发电充裕度的贡献程度。 本文基于后悔度匹配机制,构建了考虑用户原始负荷特性以及行为选择动态过程的DR模型,提出了基于序贯蒙特卡洛算法的DR资源的分布式发电系统发电充裕度影响评估流程,通过算例仿真得出以下结论。 1)DR资源能够有效提高分布式发电系统的发电充裕度。在未来高比例可再生能源渗透率的主动配电网或区域能源互联网中,DR将具有一定的可靠性效益。 2)不同用户的原始负荷特性能够影响DR的可靠性效益。可中断负荷对系统发电充裕度的贡献较可转移负荷大,DR所造成的负荷反弹对系统在特定时段的发电充裕度具有一定的影响。 3)用户行为选择是影响DR可靠性效益的重要因素。基于后悔度匹配机制的用户行为模型能够刻画用户基于效益和主观随机性的行为选择策略变化,使得DR对于分布式发电系统发电充裕度的定量分析更为可信。 如何在系统调控过程中,考虑用户选择策略“后悔”的风险,使得系统中DR资源始终保持较为稳定的可用量,需要从定价机制以及DR调度策略两个层面协调考虑,是本文下一步的研究方向。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 参考文献 [1] 刘吉臻.新能源电力系统建模与控制[M].北京:科学出版社,2014:12-18. [2] 曾博,杨雍琦,段金辉,等.新能源电力系统中需求侧响应关键问题及未来研究展望[J].电力系统自动化,2015,39(17):10-18.DOI:10.7500/AEPS20150408010. ZENG Bo, YANG Yongqi, DUAN Jinhui, et al. Key issues and research prospects for demand-side response in alternate electrical power systems with renewable energy sources[J]. Automation of Electric Power Systems, 2015, 39(17): 10-18. DOI: 10.7500/AEPS20150408010. [3] HUANG D, BILLINTON R. Effects of load sector demand side management applications in generating capacity adequacy assessment[J]. IEEE Transactions on Power Systems, 2012, 27(1): 335-343. [4] ZHOU Y, MANCARELLA P, MUTALE J. Modelling and assessment of the contribution of demand response and electrical energy storage to adequacy of supply[J]. Sustainable Energy Grids & Networks, 2015, 3(3): 12-23. [5] KWAG H G, KIM J O. Reliability modeling of demand response considering uncertainty of customer behavior[J]. Applied Energy, 2014, 122(6): 24-33. [6] MOHAGHEGHI S, YANG F, FALAHATI B. Impact of demand response on distribution system reliability[C]// IEEE Power & Energy Society General Meeting, July 24-29, 2011, Detroit, USA: 7p. [7] LI Gengfeng, BIE Zhaohong, XIE Haipeng, et al. Customer satisfaction based reliability evaluation of active distribution networks[J]. Applied Energy, 2016, 162(1): 1571-1578. [8] ZHAO Chaoyue, WANG Jianhui, WATSON J P, et al. Multi-stage robust unit commitment considering wind and demand response uncertainties[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2708-2717. [9] MOSHARI A, EBRAHIMI A, FOTUHI-FIRUZABAD M. Short-term impacts of DR programs on reliability of wind integrated power systems considering demand-side uncertainties[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2481-2490. [10] YU Rongshan, YANG Wenxian, RAHARDJA S. A statistical demand-price model with its application in optimal real-time price[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 1734-1742. [11] HEGAZY Y G, SALAMA M M A, CHIKHANI A Y. Adequacy assessment of distributed generation systems using Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 2003, 18(1): 48-52. [12] LI Yanfu, ZIO E. Uncertainty analysis of the adequacy assessment model of a distributed generation system[J]. Renewable Energy, 2012, 41(2): 235-244. [14] 曾鸣,武赓,王昊婧,等.智能用电背景下考虑用户满意度的居民需求侧响应调控策略[J].电网技术,2016,40(10):2917-2923. ZENG Ming, WU Geng, WANG Haojing, et al. Regulation strategies of demand response considering user satisfaction under smart power background[J]. Power System Technology, 2016, 40(10): 2917-2923. [15] HART S, MAS-COLELL A. A reinforcement procedure leading to correlated equilibrium[M]// DEBREU G, NEUEFEIND W, TROCKEL W. Economics essays. Berlin, Germany: Springer-Verlag Berlin Heidelberg, 2001: 181-200. [16] HART S, MAS-COLELL A. A simple adaptive procedure leading to correlated equilibrium[J]. Econometrica, 2000, 68(5): 1127-1150. [17] NGUYEN D T, NEGNEVITSKY M, DE GROOT M. Market-based demand response scheduling in a deregulated environment[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 1948-1956. [18] ZHU Quanyan, SAUER P, BASAR T. Value of demand response in the smart grid[C]// IEEE Power and Energy Conference at Illinois (PECI), February 22-23, 2013, Champaign, USA: 76-82. [19] FAHRIOGLU M, ALVARADO F L. Using utility information to calibrate customer demand management behavior models[J]. IEEE Transactions on Power Systems, 2001, 16(2): 317-322. [20] 暴英凯,王越,唐俊熙,等.序贯蒙特卡洛方法在电力系统可靠性评估中的应用差异分析[J].电网技术,2014,38(5):1189-1195. BAO Yingkai, WANG Yue, TANG Junxi, et al. Analysis on differences of applying sequential Monte Carlo methods in power gird reliability assessment[J]. Power System Technology, 2014, 38(5): 1189-1195. [21] YAAGOUBI N, MOUFTAH H T. User-aware game theoretic approach for demand management[J]. IEEE Transactions on Smart Grid, 2015, 6(2): 716-725. [22] RIDER M J, LOPEZ-LEZAMA J M, CONTRERAS J A. Bilevel approach for optimal location and contract pricing of distributed generation in radial distribution systems using mixed-integer linear programming[J]. IET Generation Transmission & Distribution, 2013, 7(7): 724-734. [23] SNPOT. User’s guide for SNOPT software[EB/OL]. [2017-03-29]. http://www.sbsi-sol-optimize.com/manuals-/SNOPT%20Manual.pdf. [24] BILLINTON R, ALLAN R. Reliability evaluation of power systems[M]. New York, USA: Plenum Press, 1996. [25] 李德智,童瑞明,王昊,等.中国需求响应实践及关键支撑技术[J].供用电,2014(3):36-39.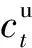


4 算例分析
4.1 DR对分布式发电系统发电充裕度的影响分析

4.2 负荷成分影响分析

4.3 用户行为影响分析


5 结论
