适用于双馈风电场联络线故障选相方法
2018-04-24王紫薇王友怀尹项根
王紫薇, 肖 繁, 王友怀, 张 哲, 尹项根
(1. 三峡大学电气与新能源学院, 湖北省宜昌市 443002; 2. 国网湖北省电力有限公司电力科学研究院, 湖北省武汉市 430077; 3. 强电磁与新技术国家重点实验室(华中科技大学), 湖北省武汉市 430074)
0 引言
双馈感应发电机(doubly-fed induction generator,DFIG)由于具有较为优异的能量转换效率及灵活的运行方式已逐步发展为风电领域的主要机型。目前,双馈风电机组一般采用单元接线方式,并联分组后就地形成集约式风电场,然后经过升压变压器和联络线连接到电网中。因此,双馈风电场联络线作为风电场向电网输送功率的重要通道,其运行安全对于风电场和电网安全稳定运行都具有重要意义。
为了防止电网故障期间风电机组大规模脱网给电网造成的冲击,确保电网安全稳定运行,并网规程中明确要求风电机组应具备良好的低电压穿越运行能力。由于双馈风电机组的短路电流特性与其低压运行控制策略以及本体保护方式等诸多因素有关,与传统的交流同步电机相比存在较大差异,使得基于传统同步电机故障特性的电网保护选相原理与算法都会受到严重挑战。中国内蒙古自治区等地区曾发生多起风电场联络线保护误选相发生的脱网事故[1-3]。为保证风电场和电网安全稳定运行,研究适用于双馈风电场联络线的选相元件具有重要意义。
由于高压系统单相重合闸、距离保护元件和故障定位等方面[4-6]的选相需要,选相元件成为高压保护装置的重要元件。对于双馈风电场联络线选相元件,文献[7-8]指出在风电系统发生故障时,由于风场侧等值电源的正负序阻抗不相等,且正序阻抗有较大波动,使得风电系统中的突变量选相元件难以满足双馈风电场联络线保护的选相需求。文献[1,9]分析了双馈型电源撬棒保护动作后可能导致传统电流选相元件存在误选相的问题,同时也指出稳态量电压选相元件可以满足双馈型电源撬棒保护动作条件下的选相需求;而文献[10]则提出了计及撬棒保护动作影响的改进电流突变量选相方案,该方案通过对电流突变量进行正序故障电流补偿来消除正、负序阻抗之间的差异,进而减小阻抗差异的影响。然而,上述分析主要针对双馈风电场撬棒电路投入的情况。事实上,在电压跌落不深的情况下,双馈机组的撬棒保护将不会动作,此时DFIG主要由转子变频器进行励磁调节控制[11-13]。在励磁调节运行状态下,DFIG馈出短路电流远较撬棒保护动作时复杂,其短路电流大小与机端电压及采用的低电压穿越控制策略相关[14-15],对联络线选相元件的影响更为严重。然而,目前研究大多侧重于DFIG在励磁调节状态下采用的低电压穿越控制策略及其故障电流特性,缺乏对联络线选相元件动作行为的分析。
为保证风电场和电网的安全稳定运行,减小因选相元件误选相造成大规模双馈风电机组脱网事故的发生,本文在分析传统选相元件应用于双馈风电场联络线存在不足的基础上,提出了基于相间电压突变量和相电压突变量幅值比较的故障选相新方法。仿真结果表明所提出的电压突变量综合选相新方法的选相性能明显优于传统电压和电流突变量选相方案,可以满足新能源电场联络线保护与重合闸的选相要求。
1 DFIG故障电流特性分析
当撬棒保护不动作时,DFIG的短路电流特性与其所采用的励磁控制策略等因素有关。根据采用的控制策略方案,文献[14-15]分别对DFIG在电网故障条件下的故障电流特性进行了分析研究,结果表明,计及励磁调节特性影响后,DFIG故障电流中只含有衰减的直流分量和基频分量,不含衰减的基频分量。因此,只需分析DFIG馈出短路电流基频分量对联络线选相元件的影响。
在对称故障条件下,根据国家电网公司颁布的《风电场接入电力系统技术规定》[16]要求,风电机组在电网故障期间应发出无功功率,以稳定电网电压和缓解电网的无功压力。在不对称故障条件下,由于DFIG定子绕组会产生不均衡发热,转矩出现脉动,输出功率发生振荡等现象[17]。为保证DFIG的运行安全,增强其低电压穿越运行能力,国内外学者提出了多种不同的控制策略[17-20],目前应用较多的主要为平衡DFIG总输出电流的控制策略。
由于突变量选相元件成立的一个前提是正序和负序电流的分流系数相等,而采用平衡总输出电流控制策略的DFIG故障电流中将不含负序分量,其对选相元件性能的影响最为严重。因此,本文基于平衡DFIG总输出电流的控制策略,建立其短路计算模型和在电网中的等值电路模型,为后续选相元件的性能评估及改进措施的提出奠定基础。
由文献[21]可知,在满足电网无功支撑需求和限制转子电流大小,以及平衡FIG总输出电流的控制策略下,DFIG定子电流的等值计算模型为:
(1)
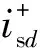
根据上式可知,DFIG在故障网络中的等效电路如图1所示。
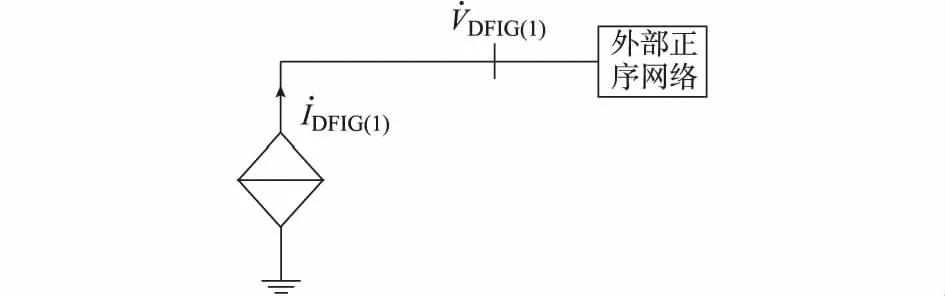
图1 DFIG的等效电路Fig.1 Equivalent circuit of DFIG
2 传统选相元件应用于双馈风电场联络线面临的问题
为分析方便,以图2中的简单电网模型为例,对传统选相元件性能进行分析评估。图中,f为短路点,DFIG为双馈风电场的等效模型,保护安装在N端。

图2 含双馈风电场的简单电网结构Fig.2 Structure of a simple grid with DFIG-based wind farms
2.1 电流突变量元件
以A相接地故障为例,对电流突变量性能进行评估。电流突变量选相元件判断电网故障为单相接地故障的选相条件是:
(2)

当f点发生A相接地故障时,N侧电流突变量选相元件有:
(3)

当线路L的M侧和N侧外部电网均为传统同步发电机电源供电时,两侧的正序和负序电流分流系数相同,电流突变量选相元件可做出正确判断,即有
(4)
然而,当N侧保护流过的短路电流主要由风电机组提供时,其短路电流特性与传统同步发电机存在较大差异。双馈风电机组在电网不对称故障条件下为正序受控电流源,不含负序电流分量,即CN2=0。此时,式(3)将改写为:
(5)
将式(5)代入式(2)可知,电流突变量选相判据不成立,无法正确选相。
2.2 电压突变量元件
对于相间补偿电压突变量选相元件[22-25],其判断单相(A相)接地短路电压突变量选相判据为:
(6)
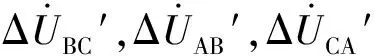
当电网电源均为传统同步发电机,且忽略正、负序阻抗参数差异,不难证明有
(7)
式中:Z1S为背侧系统等值正序阻抗;ZCM为事先整定的补偿阻抗。

然而,双馈风电机组接入后,其馈出的故障电流中不含负序电流分量,将影响电压突变量选相元件的性能。此时,线路L的N侧选相元件为:
(8)
由于N侧的双馈风电场无负序电流分量馈出,则式(8)可改写成:

(9)

2.3 突变量电压电流复合元件
由于电压突变量和电流突变量在实际应用中均存在一定的问题,文献[22]提出在电压突变量的基础上引入电流突变量构成突变量电压电流复合选相元件KΔIφφ+ΔUBC,通过综合两种选相方案的优点来改善选相元件的性能。在系统运行方式变化较大的时候,该选相方案具有较好的选相效果。但在电源正负序阻抗不等时,电压突变量选相元件和电流突变量选相元件都将失效,则KΔIφφ+ΔUBC也将失效。在风电场联络线上,由于双馈风电机组的转子绕组受变频器励磁控制,馈出平衡的三相故障电流,因此任意两相电流突变量之差均相等,则KΔIφφ+ΔUBC选相元件同样难以满足双馈风电场联络线的选相需求。
综上可知,无论电流还是电压突变量选相元件均存在一定的弱点,难以满足双馈风电场联络线保护的选相需求。
3 电压突变量综合选相新方法
为了提高风电场联络线保护的选相性能,减小双馈风电场馈出短路电流对选相元件的影响,本文提出了基于相间电压突变量和相电压突变量幅值比较的电压突变量综合选相新方法。
当电网正常运行时,故障启动元件不动作。当电网发生故障时,保护安装处故障启动元件动作,开始进行故障选相。首先根据测量电压中是否含有零序分量,判定是接地短路还是相间短路,然后进行故障相的判断。当电网发生单相接地故障时,故障相电压突变量相较于非故障相的其他相电压突变量具有更高的灵敏度(此处灵敏度定义为变化量与额定值的比值,下文同),并且健全相电压突变量的灵敏度应基本相同;而对于两相相间电压突变量来说,与故障相相关的两相相间电压突变量相较于健全相的两相相间电压突变量具有更高的灵敏度,并且含一相故障相的相间电压突变量灵敏度应基本相同。
当电网发生两相相间故障时,任一故障相的电压突变量相较于健全相的电压突变量应具有更高的灵敏度,并且两个故障相的电压突变量灵敏度应基本相同;同时,故障相的两相相间电压突变量比含一相故障相的两相相间电压突变量的灵敏度更高,且含一相故障相的两相相间电压突变量灵敏度应基本相同。而对于三相故障来说,各相电压突变量的灵敏度应相同,同时两相相间电压突变量也应相同。
(10)
式中:K1,K2和K3为故障相别选择系数。在此基础上,将K1,K2和K3的大小进行比较,可得到其从小到大的排序为:
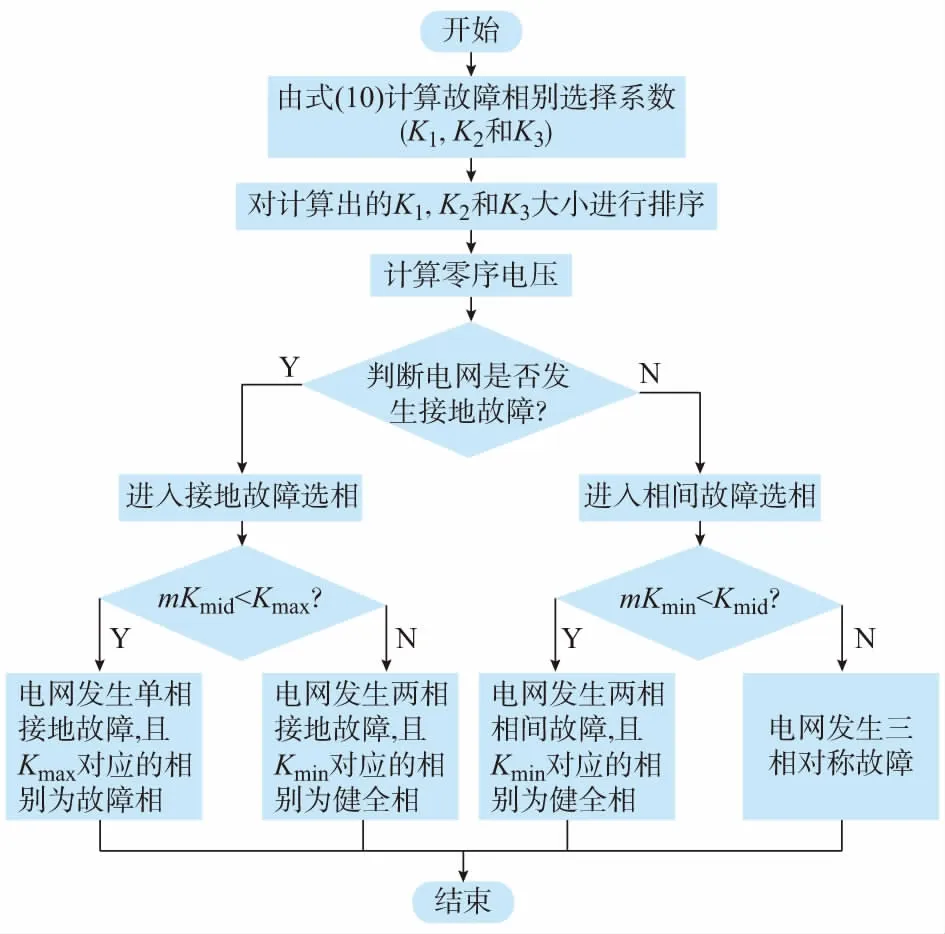
Kmin (11) mKmid (12) 式中:m为比例系数,其值与故障类型、过渡电阻大小、系统等值阻抗及故障线路的正序和零序阻抗等因素有关,主要受电网故障类型和过渡电阻大小的影响。本文根据传统电压突变量将m取值为4,在考虑实际电网可能存在的极端运行条件基础上,通过改变系统等值阻抗、过渡电阻大小和线路参数,对m取值的有效性进行了仿真验证,可适用于采用抑制负序电流的双馈风电场或光伏电站。 当式(12)成立时,判断为单相接地故障,且Kmax对应相为故障相,否则为两相接地故障,且Kmin对应的相为健全相。因此,通过判断故障相别选择系数的大小,可以对单相接地故障和两相接地故障进行正确判断。 mKmin (13) 式中:m取值同式(12)。 当上述(13)式成立时,为两相相间故障,且Kmin对应的相为健全相。在三相对称故障情况下,单相电压突变量的灵敏度类似,而两相相间电压突变量的灵敏度也基本相同,不满足上述判据。因此,通过判断故障相别选择系数的大小,同样可以区分两相相间故障和三相对称故障。 图3为双馈风电场联络线电压突变量综合选相方法流程。 图3 故障选相的流程图Fig.3 Flow chart of fault phase selection method 此外,双馈风电机组在撬棒动作条件下,其正、负序电流的基频分量同样也不相等[23]。因此,相较于传统的突变量选相方案,本文所提的选相方法在双馈风电机组撬棒动作条件下的选相性能同样具有更好的选相能力。 为了验证本文所提出双馈风电场联络线电压突变量综合选相方案的正确性,利用PSCAD/EMTDC仿真软件,构建了如图2所示的含双馈风电场接入的电网仿真模型。需要说明,在忽略风电场内部损耗的情况下,即使不同双馈风电机组的故障电流大小可能不同,但由于采用的控制策略相同,其故障电流特征应相同。在这种情况下,整个双馈风电场可以用单台DFIG等效替代。 在图2中,仿真模型中假设单位长度输电线路参数为:r(1)=r(2)=0.1 Ω/km,x(1)=x(2)=0.394 Ω/km,r(0)=0.3 Ω/km,x(0)=1.18 Ω/km,线路L的长度为100 km。接入电网的DFIG容量为49.5 MW,额定线电压为690 V;定子漏电抗为0.124 5(标幺值);转子漏电抗为0.124 5 (标幺值);定转子互感为2.176 7 (标幺值);转子额定转速为1.2 (标幺值);转子电流过流控制值Irset为1.2 (标幺值)。另外,双绕组变压器T容量均为50 MVA,变比为0.69 kV/220 kV,联结组别为Yd,漏电抗为6.5%。系统电压为220 kV,内阻为1 Ω。 附录A图A1至A3和图4 分别给出了电网单相接地故障条件下的电流突变量、单相电压突变量、两相相间电压突变量和电压突变量综合选相方法故障相别选择系数与故障时间的关系。其中,接地电阻为1 Ω,故障发生时刻为1.0 s,故障点位置为线路L上离双馈风电场保护安装处50%处,数据窗为20 ms。 由附录A图A1可知,在电网发生单相接地故障条件下,虽然接地阻抗较小,但传统电流突变量仍不能满足联络线的选相需求。这是因为在撬棒保护不动作的情况下,DFIG为受控的电流源模型,其三相电流对称,即各线电流突变量幅值基本相同,因此,电流突变量不能正确选相。由附录A图A1至A3和图4可知,虽然相间电压突变量和相电压突变量可以正确选相,但本文所提的电压突变量综合选相方法明显具有更好的选相性能。 图4 电压突变量综合选相方法(过渡电阻为1 Ω)Fig.4 Comprehensive phase selection method based on voltage difference (transition resistance is 1 Ω) 附录A图A4至图A6和图5分别给出了电网单相接地故障条件下的电流突变量、单相电压突变量和两相相间突变量,以及电压突变量综合选相方法故障相别选择系数与故障时间的关系。其中,过渡电阻为100 Ω,故障时间与故障点位置与过渡电阻为1 Ω时相同。 根据上述仿真结果,得出双馈风电场保护安装处各选相方案的计算结果如附录A表A1所示。从表A1可知,在双馈风电场联络线中点短接100 Ω阻抗发生A相接地故障时,三个电流突变量相差不大,将选相失败。电压突变量ΔUAB/ΔUBC≈2.8,同样难以满足选相需求。而电压突变量选相新方案,Kmax/Kmid≈18.3,可以正确选出故障相。 图5 电压突变量综合选相方法(过渡电阻为100 Ω)Fig.5 Comprehensive phase selection method based on voltage difference (transition resistance is 100 Ω) 在电网不同位置设置不同类型和不同接地阻抗大小的故障,以全面分析和评估基于线电压和相电压突变量幅值比较的选相方案的选相性能。附录A表A2至表A4分别给出了电压突变量综合选相方法在图2联络线L上离双馈风电场保护安装处20,50,80 km处发生不同类型故障的选相结果。 大量的仿真结果表明,本文所提的电压突变量综合选相方案不仅在单相接地故障下具有较好的选相性能,其在相间接地故障条件下的灵敏度也优于传统选相方案,可以较好地满足双馈风电场联络线的选相需求。 此外,本算法主要基于相电压突变量和相间电压突变量提出,发生三相电压互感器(TV)断线时,由于各相电压突变量和相间电压突变量变化幅值基本相同,因此,本文所提选相方案会将三相TV断线误选为三相对称故障;同时,当发生单相TV断线或两相TV断线时,TV断线所在相的相电压突变量变化较大,而含故障相的相间电压突变量变化较小,本文所提选相方案也存在误选相的情况。因此,当发生TV断线时,需要闭锁选相元件。 综上可知,受风电场复杂故障电流的影响,传统电压突变量和电流突变量选相方法已难以满足风电场联络线的选相需求,而本文所提出的电压突变量选相方案的选相性能明显优于传统电压和电流突变量选相方案,可以满足双馈风电场联络线保护与重合闸的选相要求。 本文提出了基于相间电压突变量和相电压突变量幅值比较的故障选相方法。根据双馈风电场侧保护安装处相电压突变量与相间电压突变量之间的比例关系,构建了故障相别选择系数,并根据其在不同电网故障类型下的特征,来实现故障选相。仿真研究表明,新型突变量选相方案应用于双馈风电场联络线时,较传统的电压和电流突变量选相元件具有更高的灵敏度,能够满足双馈风电场联络线保护与重合闸的选相要求。 需要说明,所提故障选相方法应用于双馈风电场联络线时,主要针对双馈风电机组撬棒保护不动作条件下DFIG采用平衡DFIG总输出电流的控制策略的情况。同时,由于光伏电源逆变器的控制策略一般也采用抑制负序电流的控制策略,因此,本文所提的选相方案也适用于接入220 kV电网的光伏电站联络线。下一步将在考虑新能源电源不同控制策略的基础上,对含新能源电源接入的电网保护新原理展开研究。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 参考文献 [1] 张保会,王进,原博,等.风电接入对继电保护的影响(四)—风电场送出线路保护性能分析[J].电力自动化设备,2013,33(4):1-5. ZHANG Baohui, WANG Jin, YUAN Bo, et al. Impact of wind farm integration on relay protection(4): performance analysis for wind farm outgoing transmission line protection[J]. Electric Power Automation Equipment, 2013, 33(4): 1-5. [2] 赵喜,赵桂廷,王蕴敏,等.基于RTDS的风电场接入系统线路保护试验分析[J].内蒙古电力技术,2013,31(2):31-35. ZHAO Xi, ZHAO Guiting, WANG Yunmin, et al. Analysis of line protection experiment with wind farm integration into power grid based on RTDS[J]. Inner Mongolia Electric Power, 2013, 31(2): 31-35. [3] 彭东虎,曹娜,于群.风电场对继电保护选相元件的影响与改进[J].可再生能源,2014,32(4):418-423. PENG Donghu, CAO Na, YU Qun. Impact of wind farm on phase selector of relay protection and improvement[J]. Renewable Energy Resources, 2014, 32(4): 418-423. [4] 李斌,李永丽,盛鵾,等.带并联电抗器的超高压输电线单相自适应重合闸的研究[J].中国电机工程学报,2004,24(5):52-56. LI Bin, LI Yongli, SHENG Kun, et al. The study on single-pole adaptive reclosure of EHV transmission lines with the shunt reactor[J]. Proceedings of the CSEE, 2004, 24(5): 52-56. [5] 毛鹏,戴斌,白日昶.一种新型振荡中故障选相元件[J].电力系统自动化,2009,33(5):61-65. MAO Peng, DAI Bin, BAI Richang. A new type of fault phase select or during power swing[J]. Automation of Electric Power Systems, 2009, 33(15): 61-65. [6] 季涛.利用电磁式电压互感器实现小电流接地系统行波故障定位和选相[J].电工技术学报,2012,27(8):172-178. JI Tao. Study of the fault location and fault phase position selection based on traveling waves using electromagnetic voltage transformer in neutral non-effective grounding system[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 172-178. [7] 王晨清,宋国兵,汤海雁,等.选相及方向元件在风电接入系统中的适应性分析[J].电力系统自动化,2016,40(1):89-95.DOI:10.7500/AEPS20150601016. WANG Chenqing, SONG Guobing, TANG Haiyan, et al. Adaptability analysis of phase selector and directional relays in power system integrated with wind farms[J]. Automation of Electric Power Systems, 2016, 40(1): 89-95. DOI: 10.7500/AEPS20150601016. [8] 滕予非,行武,张宏图,等.风力发电系统短路故障特征分析及对保护的影响[J].电力系统保护与控制,2015,43(19):29-36. TENG Yufei, XING Wu, ZHANG Hongtu, et al. Analysis of characteristics of short circuit fault of wind power system and the impact on the protection[J]. Power System Protection and Control, 2015, 43(19): 29-36. [9] 沈枢,张沛超,方陈,等.双馈风电场故障序阻抗特征及对选相元件的影响[J].电力系统自动化,2014,38(15):87-92.DOI:10.7500/AEPS20130911008. SHEN Shu, ZHANG Peichao, FANG Chen, et al. Characteristics of sequence impedance of DFIG plant and influence on phase selector[J]. Automation of Electric Power Systems, 2014, 38(15): 87-92. DOI: 10.7500/AEPS20130911008. [10] 黄涛,陆于平.适用于双馈风电场的改进电流突变量选相元件[J].电网技术,2015,39(10):2959-2964. HUANG Tao, LU Yuping. Improved superimposed current phase selector applied to DFIG-based wind farm[J]. Power System Technology, 2015, 39(10): 2959-2964. [11] 贺益康,胡家兵.并网双馈异步风力发电机运行控制[M].北京:中国电力出版社,2011. [12] 雷亚洲,GORDON Lightbody.国外风力发电导则及动态模型简介[J].电网技术,2005,25(12):27-32. LEI Yazhou, GORDON Lightbody. An introduction on wind power grid code and dynamic simulation[J]. Power System Technology, 2005, 25(12): 27-32. [13] TSILI M, PAPATHANASSIOU S. A review of grid code technical requirements for wind farms[J]. IET Renewable Power Generation, 2009, 3(3): 308-332. [14] 孔祥平,张哲,尹项根,等.计及励磁调节特性影响的双馈风力发电机组故障电流特性研究[J].电工技术学报,2014,29(4):256-265. KONG Xiangping,ZHANG Zhe,YIN Xianggen, et al. Fault current characteristics of DFIG considering excitation and regulation characteristics[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 256-265. [15] OUYANG J, XIONG Xiaofu. Dynamic behavior of the excitation circuit of a doubly-fed induction generator under a symmetrical voltage drop[J]. Renewable Energy, 2014, 71(11): 629-638. [16] 国家电网公司.风电场接入电力系统技术规定:GB/T 19963—2011[S].2011. [17] CHEN S Z, CHEUNG N C, WONG K C, et al. Integral sliding-mode direct torque control of doubly-fed induction generators under unbalanced grid voltage[J]. IEEE Transactions on Energy Conversion, 2010, 25(2): 356-368. [18] HU J, HE Y. Modeling and enhanced control of DFIG under unbalanced grid voltage conditions[J]. Electric Power Systems Research, 2009, 79(2): 273-281. [19] 郑艳文,李永东,柴建云,等.不平衡电压下双馈发电系统控制策略[J].电力系统自动化,2009,33(15):89-93. ZHENG Yanwen, LI Yongdong, CHAI Jianyun, et al. Research on control strategy for doubly-fed generation system under unbalanced voltage condition[J]. Automation of Electric Power Systems, 2009, 33(15): 89-93. [20] 王宏胜,章玮,胡家兵,等.电网电压不对称故障条件下DFIG风电机组控制策略[J].电力系统自动化,2010,34(4):97-102. WANG Hongsheng, ZHANG Wei, HU Jiabing, et al. A control strategy for doubly-fed induction generator wind turbines under asymmetrical grid voltage conditions caused by faults[J]. Automation of Electric Power Systems, 2010, 34(4): 97-102. [21] 肖繁,张哲,尹项根.含双馈风电机组的电力系统故障计算方法研究[J].电工技术学报,2016,31(1):14-23. XIAO Fan, ZHANG Zhe, YIN Xianggen. Fault calculation method of power system including doubly-fed induction generators[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 14-23. [22] 杨宇全,温渤婴,欧阳强,等.110 kV线路距离保护的复合选相元件[J].继电器,2006,34(5):10-20. YANG Yuquan, WEN Boying, OUYANG Qiang, et al. Complex selector for the distance protection of 110 kV transmission line[J]. Relay, 2006, 34(5): 10-20. [23] 孔祥平,张哲,尹项根,等.计及撬棒保护影响的双馈风力发电机组故障电流特性研究[J].电工技术学报,2015,30(8):1-10. KONG Xiangping, ZHANG Zhe, YIN Xianggen, et al. Study of fault current characteristics of DFIG considering impact of crowbar protection[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 1-10. [24] 陈鹏,张哲,尹项根,等.计及GSC电流和控制策略的DFIG稳态故障电流计算模型[J].电力系统自动化,2016,40(16):8-16.DOI:10.7500/AEPS20150610008. CHEN Peng, ZHANG Zhe, YIN Xianggen, et al. Steady fault current calculation model of doubly-fed induction generator considering grid-side converter current and different control strategies[J]. Automation of Electric Power Systems, 2016, 40(16): 8-16. DOI: 10.7500/AEPS20150610008. [25] 朱声石.高压电网继电保护原理与技术[M].北京:中国电力出版社,2005.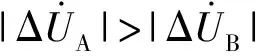

4 仿真验证


5 结语
