计及谐波功率修正的独立微电网三相潮流计算

严 鋆, 王金全, 黄克峰, 徐 晔

(陆军工程大学国防工程学院, 江苏省南京市 210007)

0 引言

独立微电网通常运行在远离大电网主网架的边远山区、海岛,可最大限度地利用分布式电源(DG)出力,提高供电可靠性[1-3]。因此,独立微电网成为保证上述地区关键负荷供电的最有效手段之一,为推动地区经济社会发展发挥着重要作用。目前,国内外针对微电网的问题研究包括系统分析、规划设计、能量管理、控制与保护等[1,4-6]诸多方面,其中潮流计算是相关问题研究的基础工作[4]。因微电网内电力电子设备的大量使用导致谐波问题尤为突出[7],有关谐波潮流问题的研究得到了较广泛的关注[8-11]。

一般而言,谐波潮流的求解以基波潮流分析为基础。文献[8-9]将微电网中的DG节点等效为常规或改进的PV,PQ,PQ(V)节点,先处理基波潮流,再采用传统或改进的谐波源恒流源模型求解微电网谐波潮流,但谐波潮流求解精度受电压畸变程度和谐波源个数影响较大[12];文献[10]利用仿射算法先求取基波条件下系统电压电流的复仿射值,再建立谐波源复仿射模型,从而求解微电网的谐波潮流,但由该方法所得谐波潮流受基波电流计算结果影响较大,显示出一定的保守性。此外,文献[11]利用径向基神经网络求解系统谐波潮流,并将计算结果应用于含非线性负荷微电网的DG功率分配和电压补偿。文献[8-11]反映的工作都是在微电网并网运行条件下进行的。

与并网微电网不同,独立微电网潮流计算具有的突出特点是[13-15]:①独立微电网系统惯性小,电网频率波动明显,不存在传统意义的平衡节点;②电网频率的波动不仅引起网络电气参数的变化,而且与DG的控制策略有关,成为潮流计算中的一个重要参数;③DG采用下垂控制时,节点类型处理应符合相应的下垂特性。基于上述特点,文献[13-14]分析了独立微电网中DG节点的类型选择及潮流计算方法,但在算例分析中并没有突出独立微电网运行中电网频率的波动性,且未考虑三相潮流问题;文献[15]尽管在独立微电网潮流分析算例中突出了电网频率的波动性,且计及三相潮流计算,但仍旧沿用了并网微电网的潮流分析方法。上述文献均未考虑独立微电网的谐波潮流问题。

文献[16]利用谐波功率计算值修正DG接入配电网下的电能计量模型,文献[17]采用谐波功率修正方法解决地铁牵引供电系统潮流计算问题;上述两篇文献尽管在所讨论的场景中未涉及独立微电网和三相潮流计算,但均为研究独立微电网的谐波潮流提供了思路。为此,本文提出一种计及谐波功率修正的独立微电网潮流计算方法。该方法基于微电网系统模型及整流装置谐波源耦合矩阵,考虑独立微电网运行控制特点及整流装置的功率特性,通过对DG节点和整流装置接口的处理,先求解交流基波三相潮流,再计算三相谐波电压和谐波电流,并以谐波功率对基波功率的修正偏差作为潮流计算的收敛条件。算例分析表明,采用本文提出的潮流计算及功率修正方法得出的潮流结果与时域仿真结果之间具有较好的对应关系,验证了所提方法的有效性。

1 微电网系统模型

微电网的潮流计算以稳态建模为基础,主要包括常规元件模型(例如变压器模型、线路模型、负荷模型等)和DG模型。在独立微电网中,稳态建模过程需考虑系统频率波动对模型参数的影响[13]。考虑到微电网具有三相参数不对称、三相负荷不平衡的特点,建立微电网系统模型的目的是形成系统的三相导纳矩阵,并在此基础上按照基尔霍夫定律得到节点电压方程。即

YU=I

(1)

式中:Y为3n×3n阶的复数矩阵,其中n为节点数;U和I分别为三相电压、电流向量。

1.1 常规元件模型

附录A给出了微电网中变压器、线路、负荷的稳态模型。其中,变压器模型以常见的DYn11型变压器为例,线路模型计及三相π形等值电路中的相间互阻抗,负荷模型考虑三相不平衡及负荷接入点的电压、频率变化。

1.2 DG模型

独立微电网中,由于有一个或多个DG参与系统频率和电压调整,下垂节点成为潮流计算模型的研究重点[13-15]。DG按接口类型可分为旋转型和变换器型2种,其中旋转型DG通常以同步发电机为并网接口,它的P-ω下垂静特性见附录A图A3,该特性主要由旋转型DG的速度控制环节实现,而它的无功功率和电压调节由同步发电机本身的励磁调节系统实现,具体可表示为:

Eg=Eg,0+ΔEQ+ΔEU=

Eg,0+kq(Qg,ref-Qg)+ku(Ug,ref-Ug)

(2)

式中:Eg为同步发电机的电势;Eg,0为同步发电机空载电势;kq为无功调节系数;Qg,ref为无功指令值;Qg为同步发电机输出的无功功率值,即旋转型DG向电网注入的无功功率值;ku为电压调节系数;Ug,ref为电压指令值;Ug为同步发电机输出电压有效值。

与旋转型DG相对应的是,变流器型DG若参与系统频率和电压调整,常采用P-f/Q-U下垂控制策略,特性曲线见附录A图A4,则有变流器型DG的下垂节点潮流计算模型为:

(3)

(4)

式中:PG,QG,P0,ω0,E0分别为变流器型DG输出的有功功率、无功功率、额定有功功率、额定角频率和额定电压幅值;ω为稳态下的系统角频率;UPCC,1为DG并网点正序电压幅值;mp和nq分别为有功下垂增益和无功下垂增益。

当微电网内有nD个变流器型DG采用P-f/Q-U下垂控制时,为调节它们之间的功率平衡,需满足以下关系:

mp1PG1,max=mp2PG2,max=…=mpnDPGnD,max

(5)

nq1QG1,max=nq2QG2,max=…=nqnDQGnD,max

(6)

由上述分析可知,变流器型DG的P-f/Q-U下垂控制特性与旋转型DG的调速调压控制特性有所区别,因此DG的下垂节点需按照DG的类型来区分。此外,上述微电网系统模型主要在基波条件下讨论,但线路模型可扩展至谐波条件,即h次谐波下的线路导纳矩阵可表示为:

Yi-j(ωh)=

(7)

式中:ωh为h次谐波角频率;Zl为串联阻抗矩阵;Yl为并联导纳矩阵。

2 微电网谐波源模型

2.1 微电网的谐波来源

电力电子设备的应用被认为是引起微电网谐波的主要因素之一[7]。从电力电子设备在微电网中的应用分布看,微电网中可能的谐波来源主要有3类:非线性负荷产生的谐波、DG及储能系统的接口变换器产生的谐波,以及配电网的谐波渗透。其中,配电网的谐波渗透也被称为背景谐波,即是指微电网并网运行时由配电网向微电网传输的谐波,主要为5,7,11,13次等电压谐波[18-19];而在本文所讨论的独立微电网中,配电网的谐波渗透不作考虑。

以光伏发电系统、燃料电池系统为代表的变换器型DG和以蓄电池、超级电容器为代表的储能系统,通常采用电压型逆变器(voltage source inverter,VSI)为并网接口,VSI经低通滤波装置后向电网输出功率[5]。附录A图A5给出了某微电网实例中储能系统输出的电压波形及A相电压频谱分析结果,图中显示三相电压波形接近理想正弦,频谱中基波分量占比非常高,但从中性点(N)对地电压波形中仍可以看出有谐波分量存在。上述现象足以证明微电网中VSI经低通滤波后的输出电压仅含有少量谐波分量,DG及储能系统不是微电网谐波的主要来源。

随着电力电子技术的发展,现代负荷结构发生了很大的变化,越来越多的用户电气设备带有相位控制电路或整流装置,其交流侧电流中含有很高比例的谐波分量[19]。而现有微电网的系统电压等级一般在35 kV以下,直接面向用户电气设备供电,因此非线性负荷对微电网的影响不容忽视。尤其是在独立微电网中,非线性负荷产生的谐波是最主要的谐波来源。

2.2 非线性负荷的谐波源模型

非线性负荷的谐波源特性与其本身的运行控制有关,通过实测频谱或其他手段建立谐波源耦合矩阵模型被认为是非线性负荷谐波源建模的有效方法之一[12,17]。附录A图A6给出了一种典型的三相桥式相控整流装置直流电压稳定控制结构,这种控制结构通常被用于直流电机调速、直流稳压电源等[20]场合,是一种常见的非线性负荷谐波源。当三相桥式相控整流装置带反电动势负载时,其等效电路如图1所示,图中LC和L分别为换相电抗和平波电抗的等效电感;Rdc为直流负载等效电阻;Edc为直流侧等效电压源。

基于调制理论,三相桥式相控整流装置的a相各次谐波电流和谐波电压之间有如下关联矩阵[12]:

(8)

同理,在三相整流桥的b相和c相下,也可得到形如式(8)的关联矩阵。上述关联矩阵直接将整流装置端口的各次谐波电流与各次谐波电压、直流侧等效电压源之间用导纳形式关联起来,即可作为图1所示谐波源的耦合矩阵模型。

图1 三相桥式相控整流装置带负载等效电路图Fig.1 Equivalent circuit of three-phase bridge rectifier with DC load

3 潮流计算方法

由功率理论原理可知,功率的概念包括基波功率和谐波功率。当实际系统中含有谐波源时,谐波潮流和基波潮流之间存在相互影响,潮流计算必须考虑谐波因素。附录B图B1给出了计及谐波功率修正的独立微电网潮流计算过程,具体为:①读取系统结构信息和数据,形成基波和各次谐波下的节点导纳矩阵;②对DG节点和整流装置接口进行处理,将非线性谐波源视为恒功率负荷代入基波潮流计算;③计算各节点注入电流,利用牛顿—拉夫逊法和节点电压方程求解交流基波潮流,得出各个节点的基波电压幅值及相角;④根据非线性负荷的谐波特性,由谐波源耦合矩阵模型和系统的节点导纳矩阵计算出各节点的谐波电压和注入谐波电流;⑤用谐波功率对基波功率进行修正(记ΔP为有功功率偏差,ΔQ为无功功率偏差,k为迭代次数,m为节点号),并将所有负荷节点的功率修正结果代入下一次潮流计算,直到满足式(9)所示收敛条件为止。上述过程中,DG节点和整流装置接口的处理,以及谐波电压(谐波电流)计算、负荷节点功率修正是潮流计算的关键环节。

(9)

式中:ε为迭代误差。

3.1 DG节点的处理

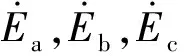
(10)

式中:Xf为DG接口变流器滤波电抗;i取a,b,c。

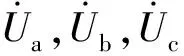
3.2 整流装置接口的处理

由2.2节可知,非线性负荷的谐波源耦合矩阵模型与整流装置本身的运行参数有关。整流装置接口的处理即是求解运行参数(假定运行参数在稳态条件下不发生变化),从而确定谐波源耦合矩阵模型。

图1所示整流装置的运行参数包括触发延迟角α、换相重叠角μ、等效电阻Rdc和等效电压源Edc,它们可通过式(11)计算[21]。由上述运行参数求解式(8)中矩阵元素的过程可参考文献[12]。

(11)

3.3 谐波电压和谐波电流的求解

已知微电网系统h次谐波下的节点电压方程为:

YhUh=Ih

(12)

其中

Uh=

Ih=

式中:Uh和Ih分别为h次谐波下各节点的三相电压列向量和三相注入电流列向量;上标1,2,…,n表示节点号。

由此,可得到节点m的基波和6l±1次谐波下的注入电流表达式为:

(13)

式中:H为计及的最高谐波次数。

由2.2节可知,谐波源耦合矩阵模型实际给出了节点m上整流装置端口的各次谐波电流和谐波电压之间的关系,与式(13)中所列电流对应。若该模型表达式与式(12)联立,将方程的实部和虚部分开求解,即可得到微电网中所有节点的各次谐波电压,以及节点m上整流装置端口的各次谐波电流。若系统中包含多个非线性负荷谐波源,则将各谐波源的耦合矩阵统一形成附录B式(B1),再与式(12)联立求解,即可反映出多谐波源之间可能存在的交互影响。

3.4 负荷节点功率修正计算方法

在电压非正弦条件下,功率计算通常被拆分为基波功率计算和谐波功率计算两个部分[22],其中谐波功率主要由谐波畸变引起,它对系统中瞬时有功功率和无功功率的传递产生影响[23]。独立微电网中的DG容量有限,在总功率不变的条件下,谐波功率的增加势必引起基波功率的减小,谐波功率对基波潮流的影响不容忽视。因此,在附录B图B1所示的潮流计算流程中,需不断通过谐波电压和谐波电流的计算结果修正负荷节点基波功率,并以修正功率偏差作为潮流计算的收敛条件。

附录B图B1中,负荷节点的基波功率修正采用下式作为基本公式,即

(14)

目前,三相非正弦条件下的功率理论主要有两种:一种是以Akagi为代表提出的瞬时无功功率(IRP)理论[24],另一种是由Czarnecki提出的电流物理分量(CPC)理论[25]。其中,IRP理论在物理意义上并没有给出完整解释,因此在描述系统功率特性时存在一定缺陷,被认为是一种有效的“实用性”理论;而CPC理论具有清晰的物理解释,克服了IRP理论存在的缺陷,对三相电路功率特性研究具有借鉴意义[22]。

CPC理论的基本原理是将时域电流信号分解成一系列具有清晰物理意义的电流分量,这些电流分量相互正交,且各自对应一个功率量,即[25]

(15)

(16)

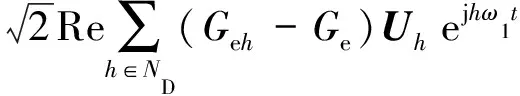
(17)

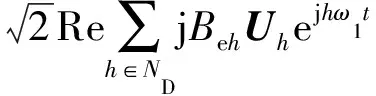
(18)

(19)

(20)

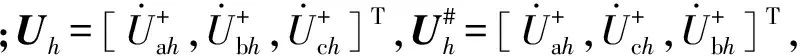
根据上述电流分量的划分方法可知,有功功率和无功功率均被认为是由电源向负荷传递的能量集合,且在三相电路中仅有正序条件下得到的有功功率具有实际意义。相关文献中,有研究者将正序条件下计算得出的有功功率称为工作功率[25]。由此,本文提出适用于含非线性负荷独立微电网三相潮流计算的基波功率修正方法,具体步骤如下。

1)提取各次谐波电压(电流)的正序分量

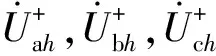
2)计算各次谐波有功功率,确定集合ND

首先,依据式(21)计算h次谐波有功功率;然后,判断Ph的符号,若Ph>0则记h∈ND。

(21)

3)计算有功功率和无功功率

在确定集合ND的基础上,依据式(22)和式(23)计算有功功率和无功功率。

(22)

(23)

4)计算基波功率修正量

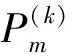
4 算例分析

4.1 算例系统

在配置2.30 GHz双核处理器、8 GB内存的计算机上,用软件MATLAB 8.3编程实现本文所提出的独立微电网潮流计算方法,并用DIgSILENT Power Factory 15程序对算例系统涉及的模型进行时域仿真。编程中,设置潮流计算迭代误差ε=10-6。

本文算例基于IEEE 9节点系统的网络结构,这种结构对于特定应用场景下提高关键负荷的供电可靠性具有积极意义。在IEEE 9节点系统的节点1处接入旋转型DG,在节点2,3处接入变流器型DG,并增加节点10,11,12,构成独立微电网系统,系统结构见附录B图B2。设系统基准容量为1 MW,基准频率为 50 Hz,取系统参考相位角为0°,其他参数设置见附录B表B2;系统中2个变流器型DG采用P-f/Q-U下垂控制,设定变流器额定频率f0和额定输出电压幅值E0均为1(标幺值)。考虑到独立微电网正常运行时的稳态频率范围为0.99～1.01(标幺值),节点电压幅值范围为 0.94～1.06(标幺值),则P-f/Q-U下垂控制中mp的取值范围为(0,0.01](标幺值),nq的取值范围为(0,0.06](标幺值),具体的DG参数见附录B表B3。

4.2 不平衡负荷下的基波潮流计算

基于上述算例系统,首先采用附录B表B4中的负荷数据(均为常规负荷),按3.1节给出的DG节点处理方法进行潮流计算,并与仿真结果比较,得到表1和表2所示的节点正序电压和DG输出有功功率。其中,方法1表示将采用P-f/Q-U下垂控制的变流器型DG等效为PV节点的处理方法,方法2表示3.1节采取的DG节点处理方法。

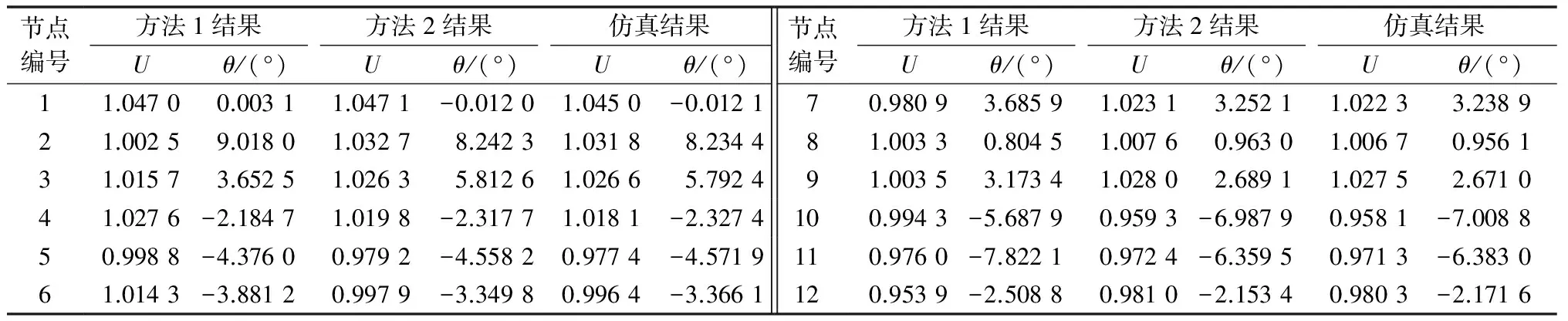
表1 各节点正序电压计算结果与仿真对比Table 1 Value comparison of positive-sequence voltages between calculation and simulation results

表2 不平衡负荷下系统频率和各DG输出的有功功率Table 2 System frequency and output power for DGs with unbalanced load

由表1可知,以时域仿真得出的节点正序电压结果为基准,采用方法2得出的节点正序电压幅值、相位角与基准的差值很小,而采用方法1得出的计算结果与时域仿真之间并不具有较好的对应关系。进一步分析可知,采用方法2计算得到的电压幅值与基准值的相对误差在0.3%以内,相位角的相对误差在0.85%以内。同理,由表2可知,将各节点DG输出三相有功功率和记为DG总输出有功功率PDG,并以时域仿真得出的PDG=3.769(标幺值)为基准,采用方法2得出的PDG值为3.765,相对误差为0.11%,而采用方法1得出的PDG值为3.755,相对误差为0.37%。此时,另由时域仿真得出的系统稳态角频率ω=0.998 5(标幺值)为基准,采用方法1、方法2得出的ω值分别为0.997 2和0.998 1,采用方法2得出的结果更为准确。由此,上述计算结果与基准值的比较,验证了本文提出的潮流计算方法在不平衡负荷条件下的有效性。

为讨论独立微电网潮流计算中的系统频率,在附录B表B4所示负荷数据的基础上增加负荷1.235+j0.712(详见附录B表B5),同理得到节点正序电压和DG输出有功功率计算结果,见附录B表B6和表B7,并可得出PDG计算结果为5.015。此时,因系统总负荷增加,经计算得到的ω值由0.998 1下降至0.996 9,表明电网频率成为独立微电网潮流计算中的一个变量。相比之下,将采用相同负荷数据但设定节点1为平衡节点(U=1.040,θ=0°)条件下所得节点正序电压计算结果在附录B表B6中进行比较,可知若在独立微电网中设置平衡节点,则电网频率将成为潮流计算中的恒定量,与独立微电网的运行特点不符,文中所提出方法更适合于独立微电网潮流计算。

4.3 非线性负荷下的潮流计算

在4.1节给出的算例系统中,将节点12接入如图1所示的三相相控整流装置,成为非线性负荷节点,详细负荷数据见附录B表B8。按本文提出的潮流计算方法得到DG输出有功功率结果如表3所示,并与未采取谐波功率修正情况下的结果相对比。表3中,方法1表示未采取谐波功率修正的传统方法,方法2表示计及谐波功率修正的潮流计算方法。

表3 非线性负荷下各DG输出的有功功率结果Table 3 Results of output power for DGs with nonlinear load

由表3可知,在非线性负荷条件下,以时域仿真得出的DG输出有功功率为基准,采用方法2得到的DG总输出有功功率为3.763,与基准值3.771的相对误差为0.21%,而采用方法1得到的DG总输出有功功率为3.870,与基准值3.771的相对误差为2.63%。显然,计及谐波功率修正后的潮流计算结果准确度更高。

进一步地,附录B图B3给出了系统各节点电压畸变率分析结果,表明采用本文提出的潮流计算方法得到的各节点电压畸变率与时域仿真结果对应较好。同时,附录B图B4给出了潮流计算迭代收敛特性分析结果,表明采用本文提出的潮流计算方法与传统方法相比,其收敛性并无显著差异(第8次迭代后的误差小于10-13)。上述对比分析验证了所提出的潮流计算方法在非线性负荷条件下的适用性。

由4.1节和4.2节给出的负荷数据及分析结果可知,在上述两种负荷条件下,若系统中各负荷节点的三相有功功率和相等,则DG输出的总有功功率值是接近的。由此表明,负荷功率PL的设定值是包含基波功率和谐波功率在内的综合值,即在负荷消耗的功率中,既包含基波分量又包含谐波分量,这与系统中负荷运行的实际情况相符。

5 结论

本文以微电网系统模型和整流装置的谐波源耦合矩阵模型为基础,提出了一种计及谐波功率修正的独立微电网潮流计算方法:首先,读取系统结构信息和数据,形成基波和各次谐波下的节点导纳矩阵;其次,通过对DG节点和整流装置接口的处理,先将非线性谐波源视为恒功率负荷代入求解交流基波三相潮流,再计算各节点三相谐波电压和注入谐波电流;最后,利用谐波功率对基波功率进行修正,将所有负荷节点的基波功率修正结果代入下一次潮流计算,直至功率修正偏差满足潮流收敛条件。

上述方法的特点是:①在DG节点的处理上,从控制角度将独立微电网中的旋转型DG和变流器型DG分别讨论,得到不同的下垂节点处理方法;②基于独立微电网中整流装置的功率特性和CPC的划分方法,进一步提出适用于潮流计算的基波功率修正方法。算例分析表明,不论是不平衡负荷条件,还是非线性负荷条件,采用本文所提潮流计算及功率修正方法得出的独立微电网潮流结果与时域仿真结果之间具有较好的对应关系,验证了所提方法的有效性。

文中所提出潮流计算方法假定稳态条件下非线性负荷的运行参数(例如触发延迟角α、等效电阻Rdc等)不发生变化,后续开展的工作是计及由上述运行参数改变引起的负荷节点功率变化情况,研究由负荷功率变化带来的连续潮流问题。此外,随着独立微电网系统规模的扩大及非线性负荷节点的增多,文中采用的迭代算法在计算效率上具有一定的局限性。在潮流计算问题的进一步研究中,将考虑多谐波源之间的抵消或补偿,以及谐波谐振等多重因素的影响,并提高潮流迭代的计算效率。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 马艺玮,杨苹,王月武,等.微电网典型特征及关键技术[J].电力系统自动化,2015,39(8):168-175.DOI:10.7500/AEPS20140908002.

MA Yiwei, YANG Ping, WANG Yuewu, et al. Typical characteristics and key technologies of microgrid[J]. Automation of Electric Power Systems, 2015, 39(8): 168-175. DOI: 10.7500/AEPS20140908002.

[2] 刘梦璇,郭力,王成山,等.风光柴储孤立微电网系统协调运行控制策略设计[J].电力系统自动化,2012,36(15):19-24.

LIU Mengxuan, GUO Li, WANG Chengshan, et al. A coordinated operating control strategy for hybrid isolated microgrid including wind power, photovoltaic system, diesel generator, and battery storage[J]. Automation of Electric Power Systems, 2012, 36(15): 19-24.

[3] 周志超,郭力,王成山,等.风柴储生物质独立微电网系统的优化规划设计[J].电力系统自动化,2014,38(7):16-22.DOI:10.7500/AEPS20130910004.

ZHOU Zhichao, GUO Li, WANG Chengshan, et al. Optimal planning and design of a wind/biomass/diesel-battery stand-alone microgrid[J]. Automation of Electric Power Systems, 2014, 38(7): 16-22. DOI: 10.7500/AEPS20130910004.

[4] 王成山,孙充勃,彭克,等.微电网交直流混合潮流算法研究[J].中国电机工程学报,2013,33(4):8-16.

WANG Chengshan, SUN Chongbo, PENG Ke, et al. Study on AC-DC hybrid power flow algorithm for microgrid[J]. Proceedings of the CSEE, 2013, 33(10): 8-16.

[5] 王鹤,李国庆,李耀峰,等.多逆变型分布式电源协调的微电网谐波控制方法[J].电力系统自动化,2014,38(23):33-39.DOI:10.7500/AEPS20140409001.

WANG He, LI Guoqing, LI Yaofeng, et al. A coordination control method of harmonic in microgrid based on multiple inverter interfaced distributed generators[J]. Automation of Electric Power Systems, 2014, 38(23): 33-39. DOI: 10.7500/AEPS20140409001.

[6] LI Yunwei, NEJABATKHAH F. Overview of control, integration and energy management of microgrids[J]. Journal of Modern Power Systems and Clean Energy, 2014, 2(3): 212-222.

[7] LI Peng, GAO Jing, XU Duo, et al. Hilbert-Huang trans form with adaptive waveform matching extension and its application in power quality disturbance detection for microgrid[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(1): 19-27.

[8] 吴杰,颜秉超,梁婷婷.含双馈风机的配电网模糊谐波潮流计算[J].电力自动化设备,2011,31(12):72-76.

WU Jie, YAN Bingchao, LIANG Tingting. Calculation of fuzzy harmonic load flow for distribution network with doubly fed induction generator[J]. Electric Power Automation Equipment, 2011, 31(12): 72-76.

[9] 杨文海,黄玲玉,程华新,等.适用于不同随机变量的主动配电网拉丁超立方抽样法概率谐波潮流计算[J].中国电力,2017,50(4):59-65.

YANG Wenhai, HUANG Lingyu, CHENG Huaxin, et al. Probabilistic harmonic power flow based on Latin hypercube sampling applied to different random variable for active distribution network[J]. Electric Power, 2017, 50(4): 59-65.

[10] 王守相,张颖,韩亮.配电系统三相不确定谐波潮流的复仿射计算方法[J].电力系统自动化,2015,39(7):41-46.DOI:10.7500/AEPS20140625017.

WANG Shouxiang, ZHANG Ying, HAN Liang. A complex affine calculating method for three-phase uncertain harmonic power flow[J]. Automation of Electric Power Systems, 2015, 39(7): 41-46. DOI: 10.7500/AEPS20140625017.

[11] BAGHAEE H R, MIRSALIM M, GHAREHPETAN G B, et al. Nonlinear load sharing and voltage compensation of microgrids based on harmonic power-flow calculations using radial basis function neural networks[J/OL]. IEEE Systems Journal[2017-01-16]. DOI: 10.1109/JSYST. 2016.2645165.

[12] SUN Y, ZHANG G, XU W, et al. A harmonically coupled admittance matrix model for AC/DC converters[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1574-1582.

[13] 彭寒梅,曹一家,黄小庆.基于BFGS信赖域算法的孤岛微电网潮流计算[J].中国电机工程学报,2014,34(16):2629-2638.

PENG Hanmei, CAO Yijia, HUANG Xiaoqing. Power flow calculation of islanded microgrids based on BFGS trust region method[J]. Proceedings of the CSEE, 2014, 34(16): 2629-2638.

[14] 李培帅,施烨,吴在军,等.孤岛微电网潮流的类奔德斯分解算法[J].电力系统自动化,2017,41(14):119-125.DOI:10.7500/AEPS20160627002.

LI Peishuai, SHI Ye, WU Zaijun, et al. Power flow calculation method similar to Benders decomposition for islanded microgrid[J]. Automation of Electric Power Systems, 2017, 41(14): 119-125. DOI: 10.7500/AEPS20160627002.

[15] 王聪,颜伟,赵霞,等.考虑逆变电源控制模式的微电网三相潮流模型[J].中国电机工程学报,2015,35(12):2960-2967.

WANG Cong, YAN Wei, ZHAO Xia, et al. Three-phase power flow model for microgrid considering inverter control modes[J]. Proceedings of the CSEE, 2015, 35(12): 2960-2967.

[16] 窦晓波,杨磊,马建,等.适应分布式光伏动态特性的改进电能计量模型[J].电力自动化设备,2017,37(10):40-48.

DOU Xiaobo, YANG Lei, MA Jian, et al. Improved model for power metering based on dynamic characteristics of distributed photovoltaic power generation[J]. Electric Power Automation Equipment, 2017, 37(10): 40-48.

[17] 胡海涛,何正友,王江峰.考虑谐波功率修正的地铁交直流潮流计算方法[J].中国电机工程学报,2012,32(34):112-119.

HU Haitao, HE Zhengyou, WANG Jiangfeng. AC/DC power flow calculation method for metro system considering harmonic power[J]. Proceedings of the CSEE, 2012, 32(34): 112-119.

[18] 沈虹,贺勇凯,韩瑞静,等.配电网系统背景谐波衰减控制研究[J].太阳能学报,2016,37(4):838-846.

SHEN Hong, HE Yongkai, HAN Ruijing, et al. Research of novel background harmonic mitigating strategy in distribution power system[J]. Acta Energiae Solaris Sinica, 2016, 37(4): 838-846.

[19] 姚勇,朱桂萍,刘秀成.谐波对低压微电网运行的影响[J].中国电力,2010,43(10):11-14.

YAO Yong, ZHU Guiping, LIU Xiucheng. Harmonics influences on the operation of LV microgrids[J]. Electric Power, 2010, 43(10): 11-14.

[20] 王仕韬,吕征宇,张德华,等.一种高功率因数的晶闸管多脉整流器[J].电力系统自动化,2012,36(24):74-78.

WANG Shitao, LÜ Zhengyu, ZHANG Dehua, et al. A muti-pulse thyristor rectifier with high power factor[J]. Automation of Electric Power Systems, 2012, 36(24): 74-78.

[21] 陈坚,康勇.电力电子学——电力电子变换和控制技术[M].北京:高等教育出版社,2011.

[22] 肖湘宁,罗超,陶顺.电气系统功率理论的发展与面临的挑战[J].电工技术学报,2013,28(9):1-10.

XIAO Xiangning, LUO Chao, TAO Shun. Development and challenges of power theory in electrical power system[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 1-10.

[23] 罗超,陶顺,肖湘宁,等.瞬时无功功率理论与电流物理分量理论的比较与分析[J].电力系统自动化,2013,37(23):130-135.

LUO Chao, TAO Shun, XIAO Xiangning, et al. Comparison and analysis of instantaneous reactive power theory and currents’ physical components theory[J]. Automation of Electric Power Systems, 2013, 37(23): 130-135.

[24] AKAGI H, KANAZAWA Y, NABAE A. Instantaneous reactive power compensators comprising switching devices without energy storage components[J]. IEEE Transactions on Industry Applications, 1984, 20(3): 625-630.

[25] CZARNECKI L S. Currents’ physical components (CPC) concept: a fundamental of power theory[C]// International School on Nonsinusoidal Currents and Compensation, June 10-13, 2008, Lagow, Poland: 1-11.