考虑风电场出力波动区间的电力系统静态电压稳定裕度计算

卢 苑, 林舜江, 刘明波, 杨智斌

(华南理工大学电力学院, 广东省广州市 510640)

0 引言

由于风电出力具有随机波动性,风电场接入电力系统将会对静态电压稳定水平产生不确定性影响[1-2]。而基于确定的系统运行方式和负荷增长方式的分析方法,比如连续潮流方法只能获得当前运行状态,且随着负荷增长,风电场出力保持在当前值不变条件下的静态电压稳定裕度(static voltage stability margin,SVSM)值,不能全面反映风电场出力随机波动下的SVSM情况。因此,为了保证考虑风电场出力不确定性影响的电力系统能够安全稳定运行,全面掌握风电场出力不确定性对SVSM的影响,有必要对考虑风电场出力不确定性的电力系统SVSM计算进行研究。

目前,针对电力系统不确定性问题的分析方法主要有:概率分析法[3-9]和区间分析法[10-15]。概率分析法有蒙特卡洛抽样模拟法[3-5]、以半不变量法为主的解析法[6-7]和以点估计法为代表的近似法[8-9]。蒙特卡洛抽样模拟法可以方便地模拟系统各种不确定因素,通过直接对抽样点的计算以得到结果,但是需要反复抽样的大量计算;解析法需要进行较为繁琐的数学推导,难以分析复杂问题;点估计法是根据已知随机变量的概率分布求取待求随机变量的数字特征并通过级数展开近似计算其概率分布,但是要获得已知随机变量准确的概率分布需要大量统计工作,并且采用不同级数进行展开对结果有很大影响。因此,对于随机不确定量概率分布不精确但能获取其波动范围上下界时,采用区间分析方法非常适用,仅需关注变量的外延信息,而获取不确定量的边界信息较容易,所需统计信息较少[13];并且,通过仿射算术的引入能有效解决区间膨胀问题,获得更加准确的结果[14-15]。显然,考虑风电场出力的波动区间情况下,对应的系统SVSM也是区间值,如何计算需作进一步研究。然而,目前对于含风电不确定性的SVSM进行区间分析的研究甚少,而且鲜有对考虑区间不确定量之间的相关性进行研究的报道。

鉴于此,本文针对风电出力不确定性的区间数表示,基于仿射区间法和连续潮流法,对不同类型极限分岔点分别求取其SVSM区间。并且通过引入区间变量相关角的概念表示区间变量的相关性[16-17],研究了考虑多风电场出力相关性下,SVSM区间值的求解方法以及分岔点类型的分布情况。

1 含风电的SVSM计算方法

1.1 SVSM计算的连续潮流法

连续潮流法采用了延拓法原理来计算静态电压稳定极限点,从系统初始运行点开始,在给定的系统负荷增长方式下进行预测、校正,求出下一步准确潮流解,从而得到一条解的路径,即PV曲线。连续潮流基本方程可表示为如下扩展潮流方程:

f(θ,V,λ)=0

(1)

式中:θ和V分别为节点电压相角和幅值向量;λ为负荷增长参数。

本文采用弧长校正环节,整个计算过程的原理见附录A图A1,具体计算过程参见文献[18]。静态电压稳定极限点即对应于负荷增长参数的最大值λmax处有dλ=0。λmax也称为系统的SVSM。

1.2 含风电的SVSM计算原理

由于风速具有不确定性,导致风电场有功出力的随机波动,可采用区间数[P-,P-]表示,假设风电场以恒定功率因数运行,在已知有功功率前提下,通过设定功率因数可得到无功功率,即视风电场并网节点为PQ节点,则风电场输出的无功功率为:

Q=Ptanφ

(2)

式中:φ为风电场运行的功率因数角。本文假定通过风电场的控制使功率因数为1,即注入电网无功功率为零。

本文计算的含风电场的SVSM是在已知系统的网架结构、各负荷节点的初始功率、各常规电源的初始有功出力和端电压等运行条件以及风电场有功出力波动范围给定的情况下,从初始运行点开始计算系统在某个给定负荷增长方式下所能承担的最大负荷增长量的波动范围。由于风电场出力不确定性用区间数表示,导致SVSM(即λmax)也是区间数。为了得到λmax的波动区间,首先取风电节点的注入功率为区间中心值进行确定性连续潮流计算,得到对应的电压稳定极限点;接着在计算得到稳定极限点那一步的校正环节中考虑风电节点的注入有功功率为波动区间并利用仿射区间算法求出λmax的区间值。

在静态电压稳定分析中有两种类型的电压稳定极限点:鞍结型分岔(SNB)点和极限诱导型分岔(LIB)点,可以通过连续潮流法计算PV曲线拐点处是否存在发电机无功越限来判断分岔点的类型[18]。识别与计算这两种分岔点不仅可以得到系统的SVSM,还可以准确地计算在分岔点处稳定裕度对于各节点注入功率的灵敏度。如果在风电波动区间范围内对应的电压稳定极限点的分岔类型存在不同,将会影响到λmax区间值的计算。因此,为了利用仿射区间算法获得更加准确合理的SVSM区间结果,本文提出含风电场的SVSM区间计算的具体步骤如下。

步骤1:利用连续潮流法分别计算得到风电波动区间的上界和下界值所对应电压稳定极限点及分岔类型,并判断在给定的风电波动区间范围内是否出现了不同类型的分岔点:若两次计算分岔点类型一致,则近似认为该风电波动区间内没有出现不同类型的分岔点,否则反之。

步骤2:若出现了不同类型的分岔点,则采用二分法识别分岔点类型改变时对应的风电出力值[19],从而将风电出力区间分为两段对应极限点分岔类型一致的区间。

步骤3:采用连续潮流法和仿射区间法计算每段分岔点类型一致的风电出力区间对应的λmax区间值:先采用连续潮流计算该段风电出力区间中心值对应的λmax值,再根据相应分岔点类型计算λmax对风电出力的灵敏度,进而根据仿射区间法计算得到该段风电出力区间对应的λmax区间值。

步骤4:综合每段区间的结果求并集后得到在整个风电出力波动区间对应的λmax区间值。

需要说明的是,考虑到实际电网运行中静态电压稳定极限分岔点类型并不会发生很多变化,且风电出力波动量对于整个电网容量来说也比较小,故本文只研究在风电出力波动区间内最多存在一个分岔点类型变化分界的情况。

2 考虑扰动源修正的仿射区间算法

由于区间算术运算得到的区间往往比实际范围大得多,仿射区间算法通过引入仿射运算克服了区间数缺少彼此之间相关性信息的缺点,能够抑制区间数计算中的区间膨胀问题,并通过求解线性规划对仿射算术的噪声元进行优化计算以获得准确的区间收缩结果,从而在一定程度上改善了结果的保守性问题。

2.1 区间数与仿射数

区间数可以用来表示一个在一定范围内波动的不确定量:

X=[x-,x-]={x∈R|x-≤x≤x-}

(3)

式中:x-为波动下界值;x-为波动上界值。

在仿射数学中,一个不确定量可以用仿射数x～表示,x～的形式如下[20]:

x～=x0+x1ε1+x2ε2+…+xnεn=x0+∑ni=1xiεi

(4)

式中:x0为中心值;εi为噪声元,代表相互独立的不确定来源,其值为区间数[-1,1];xi为实数系数,代表εi的噪声幅值大小。

因此,若同样的噪声元εi出现在多个仿射数中,就意味着这些不确定量之间具有某种联系,使得仿射算术得到的结果比区间算术更加准确。

仿射数的基本运算定义为:

αx～+βy～+γ=(αx0+βy0+γ)+

(αx1+βy1)ε1+…+(αxn+βyn)εn

(5)

x～y～=x0+∑ni=1xiεiy0+∑ni=1yiεi=

x0y0+∑ni=1(x0yi+y0xi)εi+zhεh

(6)

式中:εh为新产生的内部噪声元;α,β,γ为常系数。

采用最保守、最简便的方法计算zh,其表达式为:

zh=∑ni=1|xi|∑ni=1|yi|

(7)

区间数和仿射数之间是可以相互转化的。设区间数X=[x-,x-],令a=(x-+x-)/2,b=(x--x-)/2,则该区间数的仿射形式为:

x～=a+bε1

(8)

给定一个仿射数x～=x0+x1ε1+x2ε2+…+xnεn,则相应的区间数为:

[x-,x-]=[x0-ξ,x0+ξ]
ξ=∑ni=1|xi|

(9)

2.2 SVSM区间计算的仿射区间算法

由于仿射算术的四则运算相对较容易,故仿射区间算法中对节点电压采用直角坐标表示。风电场出力的不确定性导致各节点电压和SVSM值也在一定范围内波动,其仿射表达式为:

e～i=ei,0+∑k∈MePi,kεPk+∑k∈MeQi,kεQk

(10)

f～i=fi,0+∑k∈MfPi,kεPk+∑k∈MfQi,kεQk

(11)

λ～max=λmax,0+∑k∈MλPmax,kεPk+∑k∈MλQmax,kεQk

(12)

式中:ei,0和fi,0分别为节点i电压实部和虚部的中心值;M为系统中接入风电场节点的个数;ePi,k和fPi,k分别为节点k注入有功波动对节点i电压实部和虚部产生的噪声幅值;eQi,k和fQi,k分别为节点k注入无功波动对节点i电压实部和虚部产生的噪声幅值;λmax,0为λmax的中心值;λPmax,k和λQmax,k分别为λmax对节点k注入有功波动和注入无功波动的灵敏度;εPk和εQk分别为在节点k注入有功和注入无功不确定性的噪声元,当控制风电场的功率因数恒为1时,εQk为0。

假定接入节点k的风电场注入有功波动区间为[P-k,P-k],则区间中心值为:

Pk,0=P-k+P-k2 ∀k∈M

(13)

以风电场功率为Pk,0进行确定性的潮流计算和连续潮流计算,可以求得中心值ei,0,fi,0,λmax,0。

通过灵敏度分析求得噪声幅值ePi,k和fPi,k,根据式(10)和式(11)可得到节点电压的仿射形式,进而计算出节点i注入电流和注入功率的仿射表达式:

I～i=I～rei+jI～imi=∑Nj=1(Gije～j-Bijf～j)+

j∑Nj=1(Gijf～j+Bije～j)

(14)

S～i=P～i+jQ～i=(e～iI～rei+f～iI～imi)+

j(f～iI～rei-e～iI～imi)

(15)

式中:Gij和Bij分别为节点导纳矩阵第i行第j列元素的实部和虚部;I～rei和I～imi分别为I～i在实部和虚部的分量;N为系统的节点总数。

由式(15)整理得到节点注入有功功率的标准仿射形式:

P～i=(e～iI～rei+f～iI～imi)=Pi,0+∑Mk=1PPi,kεPk+Phiεhi

(16)

Pi,0=ei,0Irei,0+fi,0Iimi,0

PPi,k=ei,0IPrei,k+Irei,0ePi,k+Iimi,0fPi,k+fi,0IPimi,k

Phi= ∑k∈M|ePi,k|∑k∈M|IPrei,k|+

∑k∈M|fPi,k|∑k∈M|IPimi,k|

(17)

式中:εhi为新产生的内部噪声元;Irei,0和Iimi,0分别为节点i注入电流实部和虚部的中心值;IPrei,k和IPimi,k分别为节点k注入有功波动对节点i注入电流实部和虚部产生的噪声幅值。

将式(16)对应的风电节点注入有功功率写成如下矩阵形式:

P～1

P～2

⋮

P～M=P1,0

P2,0

⋮

PM,0+PP1,1…PP1,M

PP2,1PP2,M

⋮⋮

PPM,1…PPM,MεP1

εP2

⋮

εPM+

Ph1

Ph2

⋮

PhM·εh1

εh2

⋮

εhM

(18)

式中:·号表示两个向量对应行的元素相乘。

将上式写成通用形式:

f～(εP)=A0+APεP+Ah·εh

(19)

式中:f～(εP)为风电节点注入有功仿射向量。

由于系统存在非线性,如果噪声元εP各分量取值都为[-1,1],直接代入式(12)求得的λmax区间范围往往会过宽。因此,为了得到更加准确的区间结果,需要考虑由于非线性引起的误差,利用线性规划模型优化计算对噪声元进行区间收缩以得到更窄的εP=[εPmin,εPmax][14]。由于εh代表仿射数计算过程中新产生的内部噪声元,不能被缩小,取值为[-1,1]。将εh分别取最大、最小值,即1和-1,代入式(19),得到f～(εP)的上界f-(εP)和下界f-(εP)的表达式如下:

f-(εP)=APεPmax+B1

(20)

f-(εP)=APεPmin+B2

(21)

式中:B1=A0+Ah;B2=A0-Ah。

由于风电节点注入有功波动区间向量[P-W,P-W]已知,因此,为使仿射计算得到的风电节点注入有功波动区间尽量接近已知的区间,可以利用线性规划模型式(22)和式(23)求得噪声元εP的下界和上界,即εPmin和εPmax:

min ∑k∈MεPk,min
s.t. -1≤εPmin≤1
P-W≤APεPmin+B2

(22)

max ∑k∈MεPk,max
s.t.-1≤εPmax≤1
P-W≥APεPmax+B1

(23)

仿射算法计算λmax区间的式(12)中,必须计算λmax对于风电节点注入有功灵敏度λPmax。不同类型分岔点的SVSM对节点注入有功灵敏度的计算方法可参见文献[21]。将求得的λmax,0、区间收缩结果εP以及灵敏度值λPmax代入式(12),即可得到λmax波动区间。

3 考虑多风电场相关性的SVSM计算

3.1 区间变量的相关角

若区间向量X=[X1,X2,…,Xn]中任意两个分量Xi和Xj之间存在相关性,则可以构建一个包络参数实验样本的平行四边形如图1所示[16-17],得到它们之间的相关角θij,当各区间分量的上下界取值一定,而两者的相关性发生变化时,则相关角θij发生相应改变,因此不同的角度θij反映了区间变量间的相关性程度大小。当θij=90°时,Xi和Xj相互独立,采样区域变为矩形,相当于相关系数为0;当θij=0°时,Xi和Xj完全正相关,相当于相关系数为1。

图1 相关区间变量的区间分布Fig.1 Interval distribution of related interval variables

3.2 多风电场相关性的分析处理

在一定区域范围内由于气象惯性的存在,地理位置相距较近的风电场的风速区间具有相关性,而这种相关性会转换为风电场有功出力区间的相关性。下面先以两个风电场出力区间存在相关性为例说明求解SVSM区间值的思路,并推广至3个及以上风电场的情况。

1)两风电场出力相关性的分析

设风电场1的有功出力区间为P1=[a,b],风电场2的有功出力区间为P2=[c,d],它们之间的相关角为θ12。根据不同的区间宽度及相关角大小,两风电场的出力分布可以分别用附录B图B1和B2所示两种情形的二维平行四边形表示。

从附录B图B1中看到,对P1的取值可分为3段来分析P1和P2的区间相关性,将相关分布的平行四边形ABCD分解成3个部分:三角形ABE、矩形BFDE、三角形DFC,从而可以建立两风电场有功出力区间的相关模型为:

P2=[c,(P1-a)tanθ12+c]P1=[a,e]
[c,d]P1=[e,f]
[(P1-b)tanθ12+d,d]P1=[f,b]

(24)

从附录B图B2中可以看出,对P1的取值可分为3段来分析P1和P2的区间相关性,将相关分布的平行四边形ABCD分解成3个部分:三角形AED、平行四边形DEBF、三角形BCF,从而可以建立两风电场有功出力区间的相关模型为:

P2=[c,(P1-a)tanθ12+c]P1=[a,e]
[(P1-b)tanθ12+d,(P1-a)tanθ12+c]
P1=[e,f]
[(P1-b)tanθ12+d,d]P1=[f,b]

(25)

对于附录B中所示的两风电场出力区间相关分布的平行四边形,如果其中各点对应的电压稳定极限点的分岔类型存在不同,则分岔类型的分界一般为曲线,必须先找出该分界曲线才能准确计算出SVSM对于风电场出力的灵敏度,进而应用仿射区间算法准确计算出SVSM区间。为了找到分界曲线,需要对风电场1的出力区间进行均匀离散化,将区间P1=[a,b]分成n等份,则风电场1的有功出力离散化取值为:P1=a,a+d,a+2d,…,b,其中d=(b-a)/n。

对于P1的每一个离散取值,根据建立的两风电场有功出力相关模型式(24)或式(25)可以计算得到对应的P2取值区间范围,再利用1.2节提出的含风电场的SVSM区间计算方法进行求解即可得到该P1值对应的λmax区间以及分岔点类型的变化情况,综合所有P1离散取值的结果便可获得考虑两风电场出力区间相关性的λmax区间范围。

若分布在平行四边形内各点风电场出力对应的电压稳定极限点的分岔类型都相同,即若计算平行四边形4个顶点风电场出力值得到的电压稳定极限点的分岔类型都相同,则采用去相关处理方法,将两区间变量转化为两个相互独立的区间变量,并直接采用仿射区间算法计算得到λmax区间。

通过采用广义随机空间的仿射变换技术[22-23],可以将相关区间变量转换为仿射随机空间下相互独立的区间变量。原空间直角坐标系为{O:e1,e2,…,en},建立坐标轴夹角为相关角的仿射坐标系为{O:ea1,ea2,…,ean},两坐标系有如下关系:

[ea1,ea2,…,ean]T=B[e1,e2,…,en]T

(26)

B=b110…0
b21b22…0
⋮⋮⋮
bn1bn2…bnn

(27)

式中:B为仿射坐标变换矩阵,为下三角矩阵。bij通过求解如下方程组确定:

ea1ea1=|ea1||ea1|cosθ11=1
ea1ea2=|ea1||ea2|cosθ12=cosθ12
⋮
eaieaj=|eai||eaj|cosθij=cosθij
⋮
eanean=|ean||ean|cosθnn=1

(28)

将原直角坐标系下的区间向量X=[X1,X2,…,Xn]转换为仿射坐标系下的区间向量Y=[Y1,Y2,…,Yn],则有

[X1,X2,…,Xn][e1,e2,…,en]T=

[Y1,Y2,…,Yn][ea1,ea2,…,ean]T

(29)

由式(26)和式(29)可得到两坐标系下区间向量的关系:

[X1,X2,…,Xn]=[Y1,Y2,…,Yn]B

(30)

针对两风电场出力区间相关分布的平行四边形中,若各点对应的风电出力下电压稳定极限点的分岔类型相同,则通过去相关处理得到仿射坐标空间下相互独立的区间变量,即对应第2节所述仿射区间算法中相互独立的不确定来源ε1和ε2,记为εPY1和εPY2,进而可以直接采用仿射区间算法进行求解。此时,计算λmax波动区间的式(12)转化为:

λ～max=λmax,0+λPmax,Y1εPY1+λPmax,Y2εPY2=

λmax,0+λPmax,X1∂X1∂Y1+λPmax,X2∂X2∂Y1εPY1+

λPmax,X1∂X1∂Y2+λPmax,X2∂X2∂Y2εPY2

(31)

式中:X1和X2为原坐标系下相关的两风电场出力区间变量;Y1和Y2为转换为仿射坐标系下独立的两区间变量;λPmax,X1和λPmax,X2为λmax对于两风电场出力的灵敏度;∂X1/∂Y1,∂X2/∂Y1,∂X1/∂Y2,∂X2/∂Y2为变换矩阵B中的元素。

2)3个及以上风电场出力相关性的分析

对于3个风电场,若分岔点类型存在不同,可以根据每两个风电场之间的相关角,先做出风电出力相关分布的六面体,并通过对第3个风电场出力P3的波动区间进行n等份均匀离散化,再对P3的每一个离散取值P3s,确定P1和P2的相关区间分布,相当于用P3=P3s的平面截取该六面体,得到关于P1和P2相关区间分布的平行四边形,通过计算该平行四边形对应的P1和P2出力区间的上界和下界值,再结合已知P1和P2的区间相关角,即可按照上述二维处理方法,结合附录B图B1或图B2及式(24)或式(25)进行计算,综合所有P3离散取值的结果便可得到考虑3个风电场出力区间相关性的λmax区间范围。对于4个及以上风电场,若分岔点类型存在不同,由于4维及以上空间的可视化比较困难,该方法对于4个及以上风电场就较难处理,可先将这些风电场分类成数目在3个及以下的风电场群,并假定每个风电场群中的所有风电场出力区间完全正相关(相关角为0°),再采用本文提出方法进行计算。

对于n个风电场,若分岔点类型都相同,则可以通过对n个相关区间变量进行去相关处理直接求取SVSM区间值,此时计算λmax区间的通用表达式为:

λ～max=λmax,0+λPmax,Y1εPY1+λPmax,Y2εPY2+…+λPmax,YnεPYn=λmax,0+λPmax,X1∂X1∂Y1+λPmax,X2∂X2∂Y1+…+

λPmax,Xn∂Xn∂Y1εPY1+λPmax,X1∂X1∂Y2+λPmax,X2∂X2∂Y2+…+λPmax,Xn∂Xn∂Y2εPY2+…+

λPmax,X1∂X1∂Yn+λPmax,X2∂X2∂Yn+…+λPmax,Xn∂Xn∂YnεPYn

(32)

4 算例分析

以IEEE39节点标准系统和某964节点实际省级电网为例进行计算分析,负荷增长方式采用全网负荷按初始负荷比例同时增长。采用标幺值计算,系统容量基准SB=100MVA。其中,蒙特卡洛法是通过对风电出力区间范围内进行多次风电值的随机抽样,重复对每个抽样值进行连续潮流计算获得其对应的λmax值,进而得到λmax的区间范围,用来检验本文所提方法求出的λmax区间范围是否可信。

4.1 IEEE 39节点系统

IEEE39节点系统包含有10台发电机和19个负荷[24],其中节点1至29为PQ节点,节点30、32至39为PV节点,节点31为平衡节点,各台发电机的相关参数见附录C表C1。

1)单风电场的SVSM计算

假定风电场接入节点14,其注入有功功率的波动区间为[300,500]MW。分别采用仿射区间法和蒙特卡洛法计算λmax区间。其中,蒙特卡洛法抽样3000次,假定随机变量在取值区间内呈均匀分布。通过二分法找到了分岔点类型改变时对应的风电场出力值为3.923(标幺值),两种方法获得的仿真结果如表1所示。

表1 两种方法获得的SVSM区间结果比较Table 1 Comparison of SVSM interval results obtained by two methods

从表1中可以看到:随着风电注入功率的增大,静态电压稳定分岔点类型发生了改变,当风电注入功率较小时,为SNB点;随着风电注入功率的增加,分岔点变为由节点39发电机无功越限引起的LIB点。这是因为,随着节点风电注入功率的增大,由于风电场的功率因数为1,不能向电网提供无功支撑,而风电场出力的增大会引起网络无功损耗的增加,需要系统中发电机的无功出力增加,因而出现某台发电机无功越限引起的电压崩溃,极限点分岔类型由SNB点变为LIB点。另外,本文提出方法得到的λmax区间为[0.579 1,0.581 6],蒙特卡洛法得到的λmax区间为[0.579 0,0.581 5],可以看到本文方法获得的λmax区间的精度较高。

从表1中还可以看到,若不利用线性优化模型对噪声元进行区间收缩,则得到λmax区间的结果为[0.578 3,0.582 0],以表1中蒙特卡洛法的结果为基准,可以看到,不进行区间收缩得到的λmax区间结果过宽,而本文利用线性优化模型确定噪声元范围来进行区间收缩得到结果的精确度更高。

若不考虑分岔点类型的改变,直接对整个风电场出力波动区间根据1.2节中步骤3计算SVSM区间的结果为[0.579 5,0.582 0],其中λmax对风电场出力的灵敏度是根据风电场出力区间中心值4(标幺值)对应的LIB点进行计算的。以表1中蒙特卡洛法的结果为基准,可以看到若不考虑分岔点类型的改变得到的结果精度较差。这是由于直接在整个风电波动范围求λmax区间,λmax对风电场出力的灵敏度计算不够准确,使得到结果的准确性相对偏低。因此,本文提出的方法能较准确的计算出λmax区间范围。

为分析本文提出的基于灵敏度计算的仿射区间算法在线性化过程中的精度损失,当风电场出力波动区间增大时,采用本文方法得到的SVSM区间结果如表2所示;而控制风电场的功率因数为不同值时,采用本文方法得到的SVSM区间结果如表3所示。以表中蒙特卡洛法的计算结果为基准,可以看到,随着风电场出力波动区间的增大,本文方法得到的SVSM区间的准确性仍然比较好,但计算精度会略有降低;另外,随着风电场功率因数的减小,无功功率增加,本文方法得到的SVSM区间的计算精度也会略有下降,不过准确性仍然比较好。

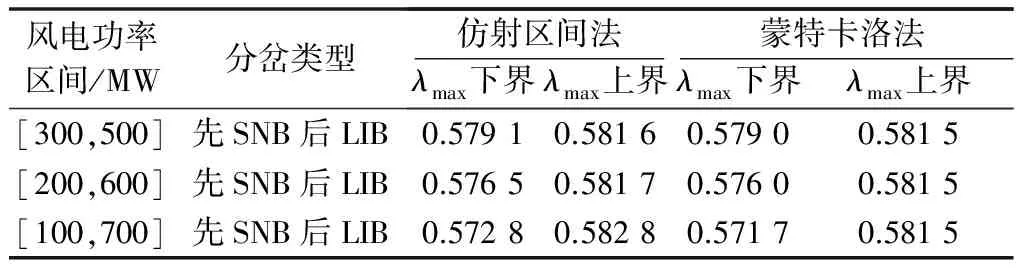
表2 风电场出力波动区间增大时的SVSM区间结果Table 2 SVSM interval results with increasing of fluctuation interval of wind farm output

2)多风电场的SVSM计算

对于两风电场的情况,假定风电场1接入节点1,其注入有功波动区间为[100,300]MW;风电场2接入节点14,其注入有功波动区间为[300,500]MW;两区间变量的相关角为80°。由于计算平行四边形4个顶点风电场出力值得到的电压稳定极限点的分岔类型存在不同,因此,采用3.2节提出的方法将区间P1=[1,3](标幺值)分成20等份,则风电场1的有功出力离散化取值为:P1=1,1.1,1.2,…,3。对每一个P1值,根据式(24)计算得到对应的风电场2有功出力区间,并采用本文方法和蒙特卡洛法计算对应的λmax区间。其中,蒙特卡洛法抽样3 000次,假定随机变量在取值区间内呈均匀分布。每一个P1取值下两种方法计算得到的λmax区间结果比较见附录D图D1。可以看出,各个P1取值下本文方法与蒙特卡洛法得到的λmax区间范围基本一致。综合所有P1离散取值对应的λmax区间范围,可得到当P1=[1,3],P2=[3,5](标幺值),且相关角为80°时,本文方法得到的λmax区间为[0.569 8,0.581 9],而蒙特卡洛法得到的λmax区间为[0.569 9,0.581 4],可见本文方法获得的λmax区间的精度较高。

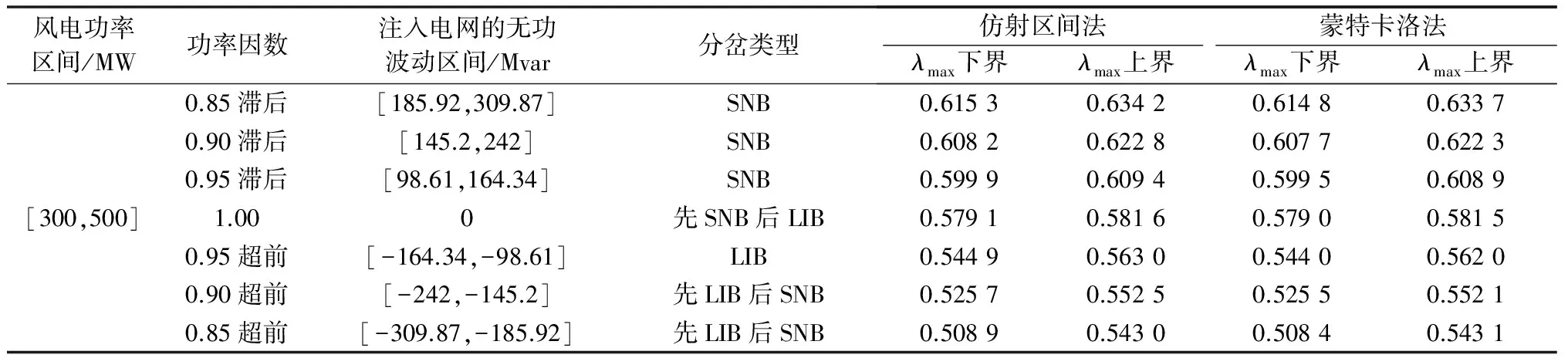
表3 风电场功率因数取不同值时的SVSM区间结果Table 3 SVSM interval results with power factor of wind farm taking different values

在考虑相关角情况下两风电场所有可能出力的情况见附录E图E1中的平行四边形所围区域;其中,折线1上的点为分岔点类型发生改变的分界点处对应两风电场的出力值,将整个平行四边形区域分为两个部分,阴影部分为SNB点对应两风电场有功出力情况,空白区域为LIB点对应两风电场有功出力情况。可以看出,随着两个风电场注入有功的增加,分岔点类型由SNB点逐渐变为LIB点。出现LIB点是由节点37或节点39发电机无功越限引起的。

对于3个风电场的情况,假定风电场1接入节点1,其注入有功波动区间为[200,400]MW,风电场2接入节点14,其注入有功波动区间为[300,500]MW,风电场3接入节点22,其注入有功波动区间为[200,400]MW;各个风电场的有功波动区间变量之间的相关角θ12,θ13,θ23均为80°。由于计算六面体8个顶点风电场出力值得到的电压稳定极限点的分岔类型存在不同,因此,根据3.2节提出的方法,将风电场3的有功波动区间P3=[200,400]分成10等份,得到风电场3的有功出力离散化取值为P3=2.0,2.2,2.4,…,4.0(标幺值);再对P3的每一个离散取值P3s,确定P1和P2的相关区间分布的平行四边形,并按照文中所述的两风电场的计算方法,最后得到的λmax区间为[0.437 6,0.526 1],而蒙特卡洛法得到的λmax区间为[0.437 3,0.525 7],可见本文方法获得的λmax区间的精度较高。

4.2 某964节点实际省级电网

该实际省级电网含有964个节点、1 026条支路和139台发电机。风电场1接入YJZ21母线,其注入有功的波动区间为[560,840]MW;风电场2接入ZHZ21母线,其注入有功的波动区间为[320,480]MW;两区间变量的相关角为40°。

由于计算平行四边形4个顶点风电场出力值得到的电压稳定极限点的分岔类型都相同,均为LIB点。因此,可采用3.2节提出的去相关处理方法将两区间变量转化为两个相互独立的区间变量并直接计算λmax波动区间,并与蒙特卡洛法计算得到的λmax区间进行比较,结果如表4所示。其中,利用蒙特卡洛法对具有相关性的两个不确定变量进行抽样时,需要先对变量进行去相关性处理,将之转换为仿射随机空间下相互独立的区间变量再进行抽样[17],接着将得到的样本点进行逆仿射变换转化为原坐标系下的样本点,然后对原坐标系下的各样本点分别进行连续潮流计算求得λmax,进而得到λmax波动区间。此处,采用蒙特卡洛法对风电场1和2的出力进行3 000次抽样,所得到的原坐标系下各样本点的分布情况见附录F图F1,可以看出,所有样本点的分布与相关角为40°的两风电场出力区间分布的平行四边形区域吻合很好。

表4 某实际省级电网计算得到的SVSM区间结果Table 4 SVSM interval results of a provincial power grid

从表4中可以看到,本文提出方法得到的λmax区间为[0.539 3,0.544 1],而蒙特卡洛法得到的λmax区间为[0.538 9,0.544 0],本文方法得到的λmax区间的精度较高,且计算量比蒙特卡洛法大大减小。

5 结论

本文将风电场出力的不确定性用区间数表示,基于连续潮流法和仿射区间算法计算系统的SVSM区间。并以相关角描述多风电场出力区间的相关性,提出了相应SVSM区间的计算方法。通过算例分析得到以下结论。

1)在仿射区间算法中利用线性优化模型确定噪声元范围来进行区间收缩,求解得到的SVSM区间与蒙特卡洛模拟法得到的区间结果很接近,因而该方法获得的区间结果具有很高的计算精度,并且相对于蒙特卡洛模拟法而言,计算量大大减小。

2)通过对不同分岔类型极限点的风电区间分别求取其SVSM区间,再综合得到的结果比忽略分岔点类型变化直接计算SVSM区间更加准确。

3)采用相关角描述风电场出力区间的相关性,对于分岔点类型存在不同时,通过对某一风电场出力区间的分段和离散化处理来得到岔点类型边界,计算得到的SVSM区间结果的精度很高;在分岔类型一致的特殊情况下,可以通过对区间变量的去相关处理,从而直接利用仿射区间算法求出SVSM区间,其结果的精度也比较高。

本文所提出方法计算考虑风电场出力波动区间的电力系统SVSM区间时,只研究了在风电场出力波动范围内分岔点类型最多发生一次改变的情况,当风电场出力波动很大时,分岔点类型可能会发生多次改变,寻找分岔点类型发生改变的边界的计算量及难度将大大增加,如何高效准确计算出SVSM区间有待进一步深入研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] VITTAL E, O’MALLEY M, KEANE A. A steady-state voltage stability analysis of power systems with high penetrations of wind[J]. IEEE Transactions on Power Systems, 2010, 25(1): 433-442.

[2] 陈海焱,段献忠,陈金富.分布式发电对配网静态电压稳定性的影响[J].电网技术,2006,30(19):27-30.

CHEN Haiyan, DUAN Xianzhong, CHEN Jinfu. Impacts of distribution generation on steady state voltage stability of distribution system[J]. Power System Technology, 2006, 30(19): 27-30.

[3] RODRIGUES A B, DA SILVA M G. Probabilistic assessment of available transfer capability based on Monte Carlo method with sequential simulation[J]. IEEE Transactions on Power Systems, 2007, 22(1): 484-492.

[4] 丁明,李生虎,吴红斌.电力系统概率充分性和概率稳定性的综合评估[J].中国电机工程学报,2003,23(3):20-25.

DING Ming, LI Shenghu, WU Hongbin. Integrated evaluation of power system adequacy and stability[J]. Proceedings of the CSEE, 2003, 23(3): 20-25.

[5] 李文沅,卢继平.暂态稳定概率评估的蒙特卡罗方法[J].中国电机工程学报,2005,25(10):18-23.

LI Wenyuan, LU Jiping. Monte Carlo method for probabilistic transient stability assessment[J]. Proceedings of the CSEE, 2005, 25(10): 18-23.

[6] SCHELLENBERG A, ROSEHART W, AGUADO J. Cumulant-based probabilistic optimal power flow (P-OPF) with Gaussian and Gamma distributions[J]. IEEE Transactions on Power Systems, 2005, 20(2): 773-781.

[7] 王成山,余旭阳.一种临界故障切除时间概率分布的求解方法[J].中国电机工程学报,2004,24(1):6-10.

WANG Chengshan, YU Xuyang. A method for computing the probability distribution of fault critical clearing time[J]. Proceedings of the CSEE, 2004, 24(1): 6-10.

[8] MORALES J M, PEREZ-RUIZ J. Point estimate schemes to solve the probabilistic power flow[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1594-1601.

[9] 杨欢,邹斌.含相关性随机变量的概率潮流三点估计法[J].电力系统自动化,2012,36(15):51-56.

YANG Huan, ZOU Bin. A three-point estimate method for solving probabilistic power flow problems with correlated random variables[J]. Automation of Electric Power Systems, 2012, 36(15): 51-56.

[10] 丁涛,崔翰韬,顾伟,等.基于区间和仿射运算的不确定潮流算法[J].电力系统自动化,2012,36(13):51-55.

DING Tao, CUI Hantao, GU Wei, et al. An uncertainty power flow algorithm based on interval and affine arithmetic[J]. Automation of Electric Power Systems, 2012, 36(13): 51-55.

[11] 王守相,张国栋,王成山.复区间潮流保守性问题的解决方案[J].电力系统自动化,2006,29(19):25-30.

WANG Shouxiang, ZHANG Guodong, WANG Chengshan. Solution to conservative property of complex interval power flow[J]. Automation of Electric Power Systems, 2006, 29(19): 25-30.

[12] 王守相,武志峰,王成山.计及不确定性的电力系统直流潮流的区间算法[J].电力系统自动化,2007,31(5):18-24.

WANG Shouxiang, WU Zhifeng, WANG Chengshan. Interval algorithm of DC power flow considering uncertainty in power systems[J]. Automation of Electric Power Systems, 2007, 31(5): 18-24.

[13] 周松林,茆美琴,苏建徽.风电功率短期预测及非参数区间估计[J].中国电机工程学报,2011,31(25):10-16.

ZHOU Songlin, MAO Meiqin, SU Jianhui. Short-term forecasting of wind power and non-parametric confidence interval estimation[J]. Proceedings of the CSEE, 2011, 31(25): 10-16.

[14] VACCARO A, CANIZARES C A, VILLACCI D. An Affine arithmetic-based methodology for reliable power flow analysis in the presence of data uncertainty[J]. IEEE Transactions on Power Systems, 2010, 25(2): 624-632.

[15] PIRNIA M. Stochastic modeling and analysis of power systems with intermittent energy sources[D]. Canada: University of Waterloo, 2011.

[16] 姜潮,郑静,韩旭,等.一种考虑相关性的概率-区间混合不确定模型及结构可靠性分析[J].力学学报,2014,46(4):591-600.

JIANG Chao, ZHENG Jing, HAN Xu, et al. A probability and interval hybrid structural reliability analysis method considering parameters’ correlation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4): 561-600.

[17] 鲍海波,韦化,郭小璇.考虑风速相关性和可调度负荷不确定性的区间最优潮流[J].中国电机工程学报,2016,36(10):2628-2637.

BAO Haibo, WEI Hua, GUO Xiaoxuan. Interval optimal power flow calculation considering interval correlated wind power and uncertain dispatchable load[J]. Proceedings of the CSEE, 2016, 36(10): 2628-2637.

[18] 刘明波,林舜江,谢敏.电力系统电压稳定分析与控制方法[M].北京:科学出版社,2017:2-10.

[19] 郑咸义,姚仰新,雷秀仁,等.应用数值分析[M].广州:华南理工大学出版社,2008:240-242.

[20] de FIGUEIREDO L H, STOLFI J. Affine arithmetic: concepts and applications[J]. Numerical Algorithms, 2004, 37: 147-158.

[21] 赵晋泉,江晓东,张伯明.用于静态稳定预防控制的新灵敏度分析法[J].电力系统自动化,2004,28(21):27-33.

ZHAO Jinquan, JIANG Xiaodong, ZHANG Boming. A new sensitivity analysis method for static stability preventive control[J]. Automation of Electric Power Systems, 2004, 28(21): 27-33.

[22] AYRES F J. Schaum’s outlines of theory and problems of projective geometry[M]. New York: McGraw-Hill Book Company, 1968: 152-155.

[23] JIANG C, HAN X, LU G Y, et al. Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(33/34/35/36): 2528-2546.

[24] 周双喜,朱凌志,郭锡玖,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社,2004:436-438.