中考数学阅读理解型试题的特点分析及教学启示

安徽省蚌埠第一实验学校

崔淮玲 汪丽娜 (邮编：638400)

1 问题提出

近年来，各地中考数学试题命制的基本理念是回归课本，注重基础性、选择性、发展性，关注关联性，突出考查数学核心素养.试题在不增加总体难度的情况下，以不同的呈现方式和思维角度，体现数学教育的基础性、选择性和发展性，挖掘数学的科学价值与人文价值.安徽2017年中考卷第19题阅读题是该卷亮点之一，体现了时代发展的新要求.一直以来，数学试题对自主学习新知识能力的考查关注较少，而自主学习能力是人们终身学习的必备能力，该题的命制意图之一就在于此，希望引导一线师生重视自主学习，关注数学核心素养的培养.关注学生数学思维的不同水平、强化思维训练、激发创新意识，提高学生学习数学的兴趣，树立科学精神，关注初高中知识衔接，重点考查学生从数学角度发现问题、提出问题、分析问题和解决问题的能力，灵活运用知识的能力等,有一定区分度，为一线教师提供了试题研究及复习教学的良好素材，对初中数学教学有很好的启示．

2 典型试题赏析

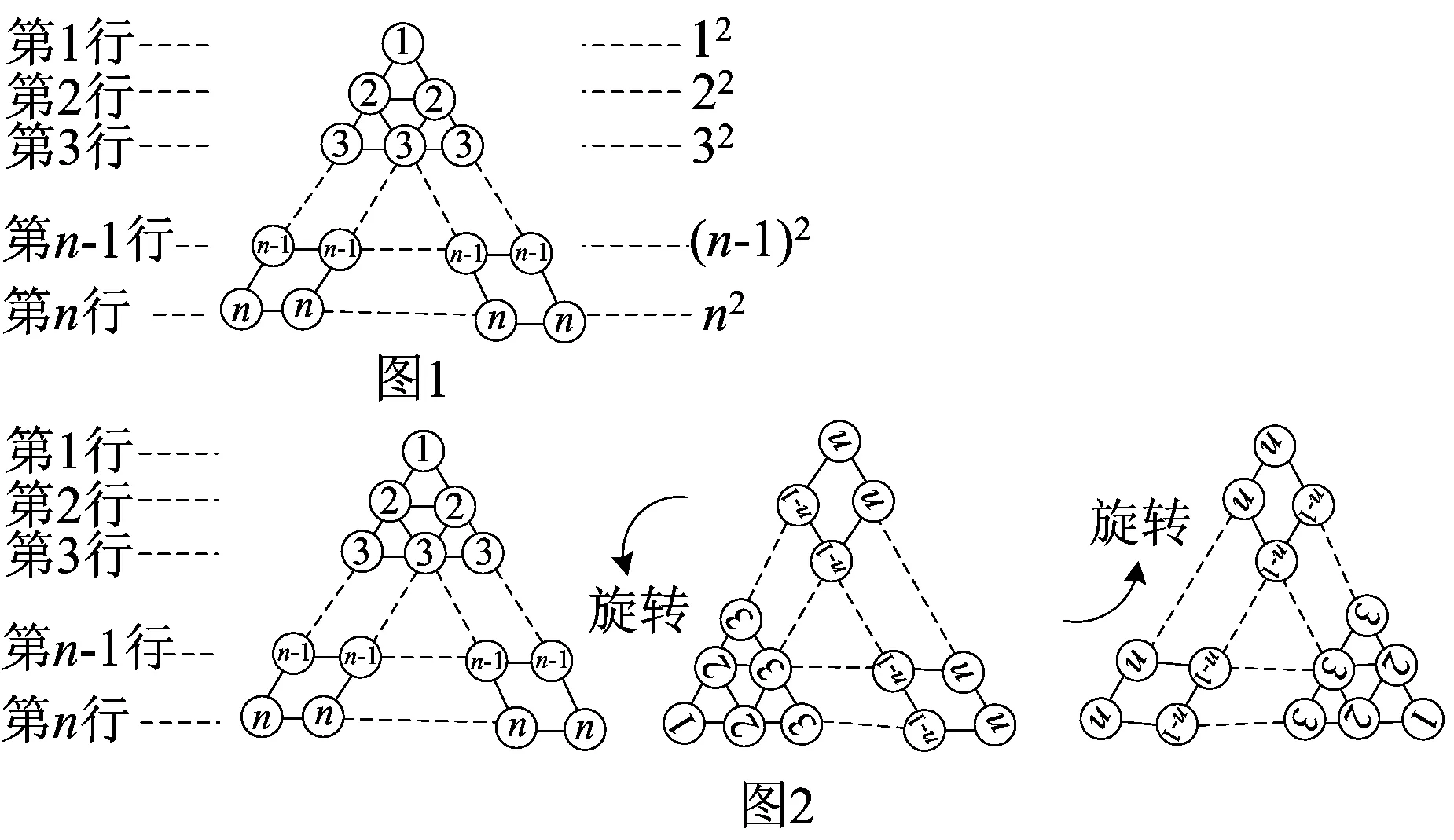
2.2 (2016·安徽第18题)(1)观察下列图

形与等式的关系，并填空：

(2)观察下图，根据(1)中结论，计算图中黑球的个数，用含有n的代数式填空：

1+3+5+…+(2n-1)+______+(2n-1)+…+5+3+1=______．

解题思路(1)根据1+3+5+7=16可得出16=42；设第n幅图中球的个数为an，列出a1，a2，a3的值，归纳可知an=1+3+5+…+(2n-1)=n2，依此规律即可解决问题；

(2)观察(1)可将(2)图中的黑球分成三部分，第1行到第n行，第n+1行，第n+2行到第2n+1行，再结合(1)的规律即可得出结论．第一个空为(2n+1),第二个空为2n2+2n+1.另外，观察(1)也可将(2)图中的黑球分成两部分，第1到第n+1行，第n+2行到第2n+1行，再结合(1)的规律即可得出结论．

2.3 (2017·张家界第20题)定义：如果一个数的平方等于-1，记为i2=-1，这个数i叫做虚数单位，把形如a+bi(a，b为实数)的数叫做复数，其中a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．

例如计算：(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i；

(1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i；

根据以上信息，完成下列问题：

(1)填空：i3=______，i4=______；

(2)计算：(1+i)×(3-4i)；

(3)计算：i+i2+i3+…+i2017．

解题思路：(1)把i2=-1代入求出即可得i3=i2·i=-i，i4=(i2)2=(-1)2=1；

(2)根据乘法分配律进行计算，再把i2=-1代入求出即可得

(1+i)×(3-4i)

=3-4i+3i-4i2

=3-i+4

=7-i；

(3)先根据复数的定义观察得in的周期性，再按周期合并即可解得i+i2+i3+…+i2017

=(i-1-i+1)+…+(i-1-i+1)+i

=i．

上述三道试题面向全体中考考生，重视有效评价，综合体现基础性、发展性，关注关联性，关注数学的深度学习；以高中数学新知识数列求和、归纳思维、复数计算为载体，巧妙设置新情境，挖掘数学学科的育人价值；突出考查从数学角度发现问题、提出问题、分析问题和解决问题的能力，考查学生的自主学习能力、逻辑推理能力和创新意识；突出考查初中数学核心素养，激发学生学习数学的兴趣，树立科学精神，为初高中数学的衔接指明方向.

3 教学启示

3.1 关注自主学习，激发学习兴趣

许多学生和家长都认为阅读理解是文科类课程学习的重要任务,而数学等理科类课程不需要阅读的,其实这种看法是非常片面的.近几年全国各地中考数学阅读理解型试题,打破了这种认识,数学不仅仅是一门自然科学,也是一种科学的语言,由于数学语言具有简洁性、严谨性、抽象性和准确性等特点,数学阅读有着不同于文科阅读的不同特点.因此，做好数学阅读理解有着极其重要的意义.数学阅读理解题注重基础性和发展性，关注关联性，培养学生从数学角度发现问题、提出问题、分析问题和解决问题的能力，培养学生用数学的眼光观察世界，发展数学抽象，提高直观想象素养，培养学生用数学的思维分析世界，发展逻辑推理能力，提高数学运算能力，培养学生用数学的语言表达世界，发展数学建模和数据分析能力、提高自主学习能力、逻辑思维能力和创新能力，提升数学思维能力，树立科学精神，挖掘数学的科学价值和人文价值，推进素质教育,对提高数学核心素养有着重要的作用[1]．

3.2 关注初高中衔接，树立科学精神

《普通高中数学课程标准(2017年版)》提出，数学核心素养是数学课程目标的集中体现，是在数学学习的过程中逐步形成的.数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展相遇的人的思维品质与关键能力.高中阶段数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学核心素养既彼此独立，又相互联系，形成一个有机整体.

关注初高中知识衔接，重视自主学习能力、创新意识、归纳和推理能力考查的趋势．提高学生数学核心素养．

中考数学承担着为高一级选拔学生的重要任务．近年来，中考数学常常在初、高中数学知识衔接处设计试题，增添了中考题的多样性与独特魅力．这类试题之所以备受瞩目，关键在于它们重理解、轻记忆，实现考查学生理解能力和应用能力的目标，体现了“终身学习 ”的理念．然而，重视初、高中数学知识的衔接，绝对不是直接讲授与初中有关的高中知识，否则既增加了学生的课业负担，又违背了中考考纲的总体要求．

在初中数学教学中要关注与高中数学知识的衔接，引导学生探究新问题，以开阔学生视野，激发学生的创新意识，培养学生的思维品质，树立科学精神．

3.3 培养思维能力，提升核心素养

首先，中考数学对“合情推理”的考查力度逐渐加大．我们知道，数学推理不仅包括分析、综合、抽象等演绎推理方式，即逻辑推理方式，而且包括观察、实验、猜想、调控等合情推理方法．前者依靠抽象思维，后者依靠直觉思维．上述两种能力的培养都需要在数学教学活动中实现．康淑敏[2]从倡导深度学习的理据：时代的学习境遇与诉求，理解深度学习的内涵特征及其价值取向，促进深度学习发展的思路三个视角认为，当今时代的知识习得以知识的创生与意义实现为目标，学习者需要具备善于思考，敢于质疑的学习品质，不断超越的探究精神，以及运用高阶认知技能深度学习的能力. 推进深度学习，应以塑造创生性文化学习为基础，强化学习者深度学习素养的培育，通过提供具有思维空间的学习任务涵养其多向思维的学习习惯和解决问题的能力，在探究过程中实现知识建构与学习迁移，从知识掌握走向智慧生成与能力发展.

其次，把培养学生的推理能力贯穿在日常教学活动中．能力的发展和知识的获得是两回事，能力的形成是一个循序渐进的过程，有其自身的特点和规律，学生“懂 ”了、“会”了某种知识并不表明能力已经形成，能力的形成是在学生自己“悟”出了道理、规律和思考方法等之后的事，这种“悟”只有在日常数学教学活动中才能得以实现．因此教学活动必须给学生提供合作交流和自主探究的空间，组织和引导学生亲历观察、实验、猜想、验证等数学活动过程，并把培养推理能力有机融合在这一过程中[3]．

综上所述，中考数学阅读理解型试题面向全体学生，关注基础性和发展性，关注关联性，挖掘数学的科学价值和人文价值，通过数学阅读，考查学生从数学角度发现问题、提出问题、分析问题和解决问题的能力，通过用数学的眼光观察世界，发展数学抽象，提高直观想象素养，用数学的逻辑分析世界，发展逻辑推理，提高数学核心素养，用数学的语言表达世界，提高数学建模和数据分析能力、自主学习能力、探究能力、归纳推理能力和创新意识，提升数学思维能力，倡导积极主动、勇于探索的学习方式，发展学生的数学应用意识，激发学生学习数学的兴趣，树立科学精神，挖掘数学的科学价值和人文价值，推进素质教育,对提高数学核心素养有着重要的作用．

1 邓莎莎. 中考数学阅读理解题的特征及教学策略研究[D].重庆师范大学,2016

2 康淑敏. 基于学科素养培养的深度学习研究[J]. 教育研究，2016(6)：111-118

3 郝娟. 新课程背景下初高中数学教学衔接问题的研究与实践[D].陕西师范大学, 2010

4 中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M].北京：北京师范大学出版社, 2012

5 中华人民共和国教育部制定. 普通数学课程标准(2017年版)[M].北京：人民教育出版社, 2018