一类条件最值问题的再研究

浙江省湖州市双林中学

李建潮 (邮编：313012)

条件最值问题已知实数x、y满足ax2+bxy+cy2=d(其中a、c、d均为正常数，b为实常数，且△=b2-4ac<0)，求z=mx+ny(m、n为实常数)的最值.

这是众多期刊探究的一类热点问题.例如，近期文[1]就以下问题专门探研了其解法.

文[1]问题 已知x2-xy+y2=3，求2x+y的最大值.

考虑到文[1]问题的解法1就把题中的x、y这个“实数”条件错误地当成了“正数”条件，故而很有必要再述文[1]问题解法之研究. 本文旨在立足高中数学给出四种有别于文[1]的求解方法，供大家参考.

解法1(减元，导数法)从x2-xy+y2=3中，解出y：

所以

(1)

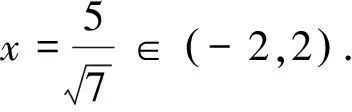
因此，当

注1事实上，结合二维柯西(Cauchy)不等式：

(ac+bd)2≤(a2+b2)(c2+d2)

(2)

(当且仅当bc=ad时，取“=”号)，解法1可优化为：

由(1)得

由注1，自然萌生了下述不等式法：

解法2(不等式法)将题设x2-xy+y2=3配方，化为

(3)

即(x+y)2+3(x-y)2=12，

所以，由Cauchy不等式(2)，立得

当且仅当

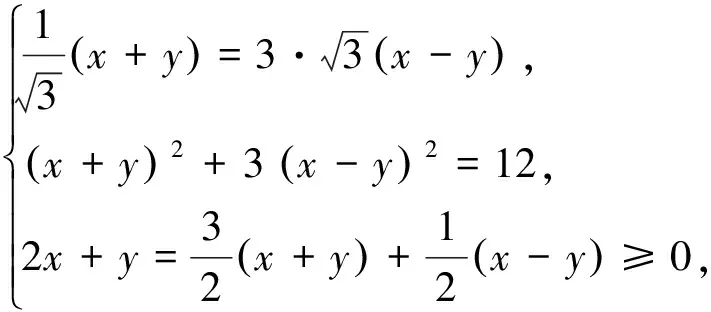
注2作为文[1]问题的第一个变形“不妨把问题改为：已知x2-xy+y2=3，求y-x的最大值”，由解法2的(3)式便可得

3(x-y)2≤(x+y)2+3(x-y)2=12，即-2≤y-x≤2.

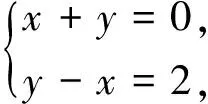
另，由解法2脱胎而来的当是将文[1]问题化归为以下线性规划问题：

解法3(换元，线性规划法)在(3)式中，令

(4)

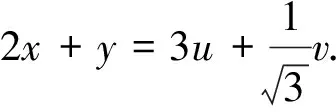
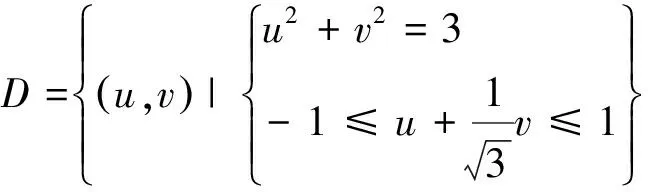
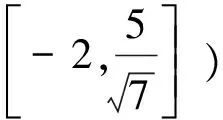
最后，我们设想：由文[1]问题题设中的代数式x2-xy+y2与题断(代数)式2x+y可否构造出一个关于x、y的二元二次齐次式的完全平方式来？于是就有了以下解法：

解法4(构造法配完全平方)可令

(2x+y)2+m(x2-xy+y2)=(4+m)x2+(4-m)xy+(1+m)y2

(5)

(其中m为待定系数)为完全平方式，其充要条件是

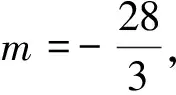
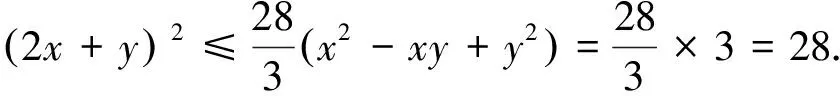
需要提及的是：以上四种解法是解文[1]问题的通法、通解(问题千变万化，方法“一成不变”)，所涉知识完全是高中数学必学内容.

1 孔德宏，贺政刚. 揭示解题方法的教学本质 改进数学解题教学[J]. 数学通报，2017(8)