由《分式》章节复习课的预设生成谈学科素养问题

浙江省宁波市镇海蛟川书院

陈 丽 (邮编：315200)

1 理论与实际的碰撞，现实与理想的焦灼

裴光亚老师说——毫无疑问，教学常态的基本特征就是匹配，教学的艺术特征就是错位.寻找合适的教学，关键要研究学生，还要研究数学史，更要立足教育的高度[1].实际教学中能够数学地提出问题的学生数量直线下降；善于数学表达的学生也在以二次方的速度递减；数学优秀生中真正喜欢数学的更是少之又少.我喜欢数学，想方设法地教上数学，进修数学，用自己的方式思考并实践着如何教得再好一些——让更多智商中等的学生也喜欢数学，让学生的学习有章可循，学得顺畅，让学生的发展得到数学最大的帮助.我的出路在哪里？下面仅以浙江版七年级下《分式》章节复习设计、课堂生成实录和自己的反思与困惑为线索展示数学教学和学科素养的“两难”的实情与“重生”的愿望.

2 忠实学生的生成，思考自我的灵感

2.1 常规方法，即兴展示

环节1(目录法整理知识和方法)要求学生根据课本目录，思考约3分钟，分层点三名同学，即兴表述自己的想法，后一个同学点评和补充前一个同学的发言，最后生成如下：

(1)概念三序列：分式定义扣三点；分式意义三方面，有意义、无意义和分式值为零；分式中最重要的三个概念，最简分式、最简公分母和增根.

(2)分式运算：分式基本性质是核心，运算法则是依据；乘除法重在约分，约分前注意因式分解，约分时要注意顺序，约分后要注意符号和位置；加减重在通分，找准最简公分母，注意互为相反数、多项式的因式分解和去添括号.

(3)分式方程：去分母法解方程，规范四步骤一去二解三验四写；应用两类型：一是实际应用题的“双验”，二是公式变形，就是解已知数是字母的分式方程.

设计意图帮助学生梳理知识，形成网络，使知识系统化，结构化，从而加深对知识的理解及知识之间的内在联系的把握，形成整体性的数学“认知框架”.复习中要求学生构建单元知识网络图表，寻找本单元的知识结构，并从教师的示例中受到启发，是促进智能迁移的有效的举措，因此此环节不但要有，而且应该在“方法”和“参与度”上多琢磨，教师教学的关键是把这些数学化很浓的知识体系语言深入浅出地表达出来，让学生易于接受，乐于接受，常见的表达方式可以有表格式、纲要式、图表式和口诀式.

2.2 常规问题，生生互动

环节2理清知识清单后，引导学生把所学知识归纳到知识体系中，弄清来龙去脉.笔者提出两个常规问题：一是分式学习的过程中，你体会到的最明显的方法是什么？分式与旧知识之间的关系如何？二是分式自身的拓展有哪些？与分式相辅相成的方法有哪些？学生发言整理如下：

(1)类比的数学思想最为明显，分式的学习思路与小学分数一脉相承，不同的是整式代替了整数，最小公倍数代替了最简公分母，最简分式代替了最简分数.

(2)整式的运算、因式分解蕴含在分式的运算中，分式乘除要约分，必须先因式分解，分式加减通分后，分子的加减就是整式的加减.

(3)分式方程与整式方程关系很密切，分式方程的问题都是转化为整式方程去解决的.

(4)繁分式的化简，分式方程的无解和增根，分式特有的分离法、倒数法、检验等等，是分式“特质”，与分式相辅相成.

设计意图把主动权充分给学生，听听学生能够表达些什么，数学的、非数学的，但教师要做到心中有数，通过常规问题的提问交流，帮学生理清整章知识的特质，将知识体系和思想方法不露痕迹地教给学生.这一环节耗时不多，但在复习课中笔者认为起着举足轻重的地位，必须要有，数学的知识体系和思想方法就好比一座建筑的地基，是数学学习的灵魂，是智慧萌发的源泉.但操作过程中要注意形式的多样性，避免千篇一律，学生出现审美疲劳.

2.3 典型问题，上台展示

环节3整理和收集本章中的典型题，四人小组交流再整理出五道，有文本留存，课堂交流要求陈述选编理由，全班展示时有重复的自动删除，展示形式不限，可板书讲解，可制作PPT,可图片错误辨析，展示评价用星级，一般耗时会在半小时左右.

四星级题目类型展示收集如下：

(1)化简计算：一道分式乘除，一道分式加减(含整式和分式加减)，老师点赞之处①分式的乘除重在约分，约分前因式分解，约分时注意“序”，约分后注意符号和位置；②分式与整式的加减法，注意把整式看做分母为“1”的式子，注意添括号和符号.

(2)化简求值：化简形式为分式乘除和加减综合，然后选择合适喜欢的字母求值，老师点赞之处是学生能诙谐地表达出——“温柔一刀”.

(3)变形求值：最好用到平方法、配方法.

(4)解分式方程：一道无解，一道有解，老师点赞之处是学生能够归纳出类型——已知分式方程解的情况，求分式方程中字母系数的取值或取值范围，还能总结出一般的解题步骤.

(5)公式变形.

(6)已知分式方程解的情况，求方程中字母系数的值或范围.

(7)凸显倒数法、分离法、整体思想的综合题.

(8)分式应用题：一道实际应用工程或行程类，一类谁合算问题.

设计意图复习课的这个环节——你方唱罢我登场，笑声和意外层出不穷，学生很喜欢！学生学习状态是课堂教学有效性的关注点，学生的学习取决于他自己做了什么，而不是教师做了什么？在这个环节中，教学预设、种种生成，需要老师把控的除了学生的智商，专业的数学知识，题目，还有不可控的情商，展示时的声音、语速、姿势甚至笑容等等，都需要教师进行表扬或指正，真正需要教师实践性的智慧，凸显教学相长！

2.4 归类提高，触类旁通

环节4笔者翻阅教参，学生作业，各种核心期刊，学生常用的教辅书等，将章节中的常考易错题，适当的新题、难题进行拓展渗透，从选题、引导讲解、归纳小结，都非常小心和用心，不断斟酌讲什么，怎么讲，尽可能多地设计预设和生成.

例如已知分式方程解的情况，求分式方程中字母系数的值或范围，笔者选取的题组如下：

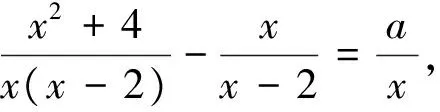
(1)无解；(2)有增根；(3)解为正数.

设计意图解决此类问题的基本步骤：一化分式方程为整式方程(去分母法)，二整理整式方程为标准形式(形如ax=b)，三是依题意得出新方程或不等式(关于字母系数的).易误之处是无解要分类，整式方程无解，整式方程有解但解为增根；增根要注意检验；解为正数或负数等等，要排除增根.这样规范解题，分析归纳之后，学生既掌握了解题的一般步骤，又明白了增根和无解的区别和联系，还知道了增根产生的根本原因——违反了等式的基本性质.再如分式方程的应用复习指导时，笔者即兴总结了基本关系式法的要点，“一个基本关系式”，“两种状态”，“算两次”，学生很是受用，频频点头.这样知识的来龙去脉，解题的要点方法，在归类中知晓，在归类中提高，所以复习课中，笔者常常提醒学生，解题三境界：做对，用最优的方法做，学会归类，我们一定要追求最高境界——学会归类！

2.5 互测互评，共同提高

环节4学习小组出一份半小时左右的训练试卷，要求完整凸显本章的知识方法，按照常考题型：易误题：适当的难题=7∶2∶1的比例，书写端正上交评比，作为集体弹性作业上交.

设计意图徐斌艳指出数学核心能力为数学的提出问题；数学表征与变换；数学推理证明；数学建模；数学地解决问题和数学交流等[2].笔者一直苦恼于学生的数学地表达不情愿和数学交流生涩，因此在复习课中安排此环节，坚持下来感觉最自豪的是——老师们上公开课，喜欢用我的班级学生，说是孩子们能讲会说，善于表达，尤其到了初三，会有更多的学生即兴走上讲台，讲得眉飞色舞，手舞足蹈，生生互动起来争论得脸红脖子粗，感染力丝毫不逊于教师.

3 心中有数，让学科素养落地有声

3.1 用心捕捉少年味道的“理性”光点，提倡个性化的理解，传承数学经典，寻找核心素养新起点

萧文强教授在《数学·数学史·数学教师》中谈到数学上的“才、学、识”兼顾才是广义的数学教育，师者具备为“学养教师”，生者具备方可体验数学的愉悦，传承数学的智慧.“识”是指分析鉴别知识再经融会贯通后获致个人见解的能力.重视这些个性化的理解，必须依赖学生参与的教学活动，依赖学生的感悟与思维，这些应该是日积月累的.自己思考的经验的积累，数学知识、技能、方法及思想不是靠讲解让学生理解，而是靠数学活动让学生掌握、感悟和内化[3].

有心积累了这届学生数学学习过程中总结的三字经四字诀：目录法，树状图，数字化，关键词，辨要点，找特质，夯四基，理思路，析典例，突重点，抓七寸，凸过程，建模型，悟思想，打比方，促理解，列图表，清思路，算两次 方程现， 编题组，善变通，练压轴，破瓶颈，练综合，提能力，易误处，显身手，常归类，集通法，问道于零，关注特殊，数看实质，式看形式，形变神似，不重不漏，数重计算，式重化简，方程重变形.

看看读读，觉得学生能够把这些“经典”言简意赅的表达出来，他们应该经历了一个怎样的过程呢？数学课上，这样的场景颇受学生喜欢：生生自由组合一个一个做点评，而后笔者会抓住学生点评中的“闪光点”进行点评.这样的设计为学生提供“做事”能力，他们要解题，要评讲，要在短时间里组织自己的语言，用自己的方式去表达，因为涉及到交流，还会有“做人”之道的“情商”，比如语言的干净利落，体态的大方，微笑地说出不足，偶尔的冷幽默等等，这些有“价值”的启蒙，可以让学生发现问题及时，指出问题有理有据，理解问题深刻细致，争论问题常态化.

3.2 潜心提取学科素养中“德性”的养分，浇灌智慧学习的花朵

德育并不一定是文科老师的专利，在数学教学中，教师也可以潜心提取学科素养中“德性”的养分，助力核心素养落地生根.比如在“分式”这一章，与分式相辅相成的思想方法有类比、转化、检验等，类比小学分数的学习经验学习分式，可让学生知道数式通性的同时，用数的经验学习式的知识，感受异同，分辨发展与变化；学习分式方程时，无论是解法还是应用，都可以上承整式方程的解题步骤，下启“检验”的必要性和相应的方法即可.类比、转化和检验这三种思想在分式学习中不断渗透，不仅解决分式问题事半功倍，同时学生数学学科素养也提升了不少.

下面分享几个笔者在平时教育教学中感受较深的“数学德育点”.

数看实质，式看形式——初一新生活既需要形式多样丰富多彩的活动，又需要体会各种活动的真谛，尽快适应新同学，新老师，新环境，新要求，就如同我们要尽快走出小学算术的乐园，尽快走进字母代数新天地！

问道于零，关注特殊——零的特殊性在实数的学习中，我们总结了若干个特性：零既不是正数也不是负数；零是最小的自然数；零的平方、立方、平方根、立方根、绝对值都是零；零大于一切负数，小于一切正数；零在加减乘除运算中的特殊性等等，学生用这种方法去解决实数的概念理解问题会方便很多，以至于生活中跟他们讲关注特殊人群，关注特殊的社会问题等深刻的道德问题甚至高深的哲学问题时，他们似乎也能深入浅出的理解.

事不过三，是我处理学生错误的原则之一，当它与“规律题”的思考方法结合在一起的时候，学生们记忆尤深——准确地找推一二三，事不过三观察猜想，用四来验证.

学以致用——学了什么，什么就是一种方法，常见的“字母代数”“方程方法”“数轴法”“绝对值法”“因式分解法”等等，都是如此产生的.而每一种方法都依托于一种知识，我们既可以理解为水到渠成，又可以理解为相辅相成，这就是思想与方法，也是数学与哲学.

很准抓“七寸”，难度大的问题，我们只要抓住它的“七寸”，如同毒蛇与巨蟒，瞬间没了攻击力；审题多方式，抓题眼，列表格，用基本关系式等等，处理问题方法总比困难多；多设元，设而不求——退一步海阔天空……

很多时候，很多地方，只要我们用心地去体会每一个教学活动，学科中“德性”的养分很多，注意汲取，注意提炼，长期以往就会沉淀出“数学的气质”——严谨，细致，灵活，有序,重点突出，及时调整……这也是教育应该追求的“素养”——十几年后，我们所学的知识用不到了，但学知识过程中培养出来的方法、能力和意志力却终身受益.

教育的真谛是教育不改变生活环境，却能改变人的思维方式，让我用萧文强教授教师的一句自勉来勉励自己吧——为教人而教书，由教书而教人，做学养型教师，学无止境，教无止境[4].

1 裴光亚. 寻找合适的教学[J].中学数学教学参考，2016(8)：卷首

2 徐斌艳.数学学科核心能力研究[J].全球教育展望,2013(6):67-74

3 史宁中.推进基于学科核心素养的教学改革[J].中小学管理,2016(2):34-54

4 萧文强.心中有数[M].大连：大连理工大学出版社,2010