一组类比三角不等式的统一证明

天津水运高级技工学校

黄兆麟 (邮编：300456)

贵刊文[1]给出并证明了如下六个含余弦函数的三角不等式:

在△ABC中,设A,B,C所对的三边为a,b,c,则有

①

②

③

acosA+bcosB+ccosC

④

a2cosA+b2cosB+c2cosC

⑤

⑥

本文给出能揭示此六个不等式本质属性的统一简证,供读者欣赏.

定理在任意△ABC中,若A≥B≥C,k∈(0,1]且当正实数x,y,z满足

(*)

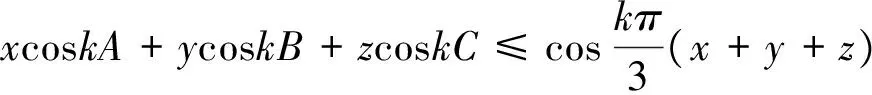
而当正实数x,y,z满足

(**)

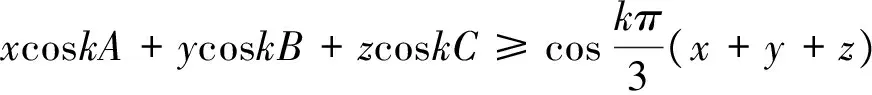
证首先证明不等式(*).

又设不等式(*)左右之差为M1，那么当x≥y≥z时就有

以上证明过程用到了一个熟知的不等式(可由凸函数的琴生不等式直接证得)

同理可证定理中的不等式(**)也成立.(由读者自行完成)

至此知定理成立.下面利用定理分别证明文[1]中的六个不等式①～⑥.

证(1) 由不等式①的全对称性,不妨设A≥B≥C,

证(2) 由不等式②的全对称性,不妨设A≥B≥C,

证(4) 由不等式④的全对称性,不妨设A≥B≥C,

那么此时可取k=1且取x=a,y=b,z=c,应用不等式(*)立得不等式(4′)成立.

(4′)

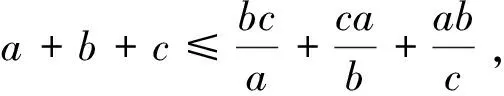
即不等式(4)成立.以上证明过程表明,不等式(4′)强于不等式(4).

证(5) 由不等式⑤的全对称性,不妨设A≥B≥C,

那么此时可取k=1且取x=a2,y=b2,z=c2,应用不等式(*)立得不等式⑤成立.

从而知不等式(3)也成立.

证(6) 由不等式⑥的全对称性,不妨设A≥B≥C,

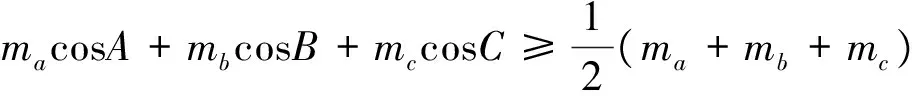
1 杨续亮,苏岳祥.一个三角不等式的类比与证明[J].中学数学教学，2017(5):76-78