本节课学到了什么？——谈高三数学复习课堂中的思维引发过程

中山大学附属中学

于君荣 (邮编：510275)

在一次“高中数学学科核心素养”的培训中，数学教育专家白涛教授给我们讲课时，提到过这样一个问题：“每节课结束时，老师们是不是会向同学问一句：‘本节课学到了什么？’之类的问题．那么，大家回忆一下，学生的回答大多是什么？”

一时间，笔者陷入了沉思：每上完一节数学课后，我们确实是常常这样总结性地问过学生类似的问题，而得到的答案大多是：“本节课我学到了什么什么知识……”如此等等，很少有同学提及到，他们或感悟或体会或掌握到了什么样的数学思想方法与思维规律．

我们不妨结合高中数学的学科特点，思考一下这个问题.在数学教学，特别是高考复习教学过程中，该如何渗透适当的数学思想方法与思维方式？如何充分利用课堂，紧抓一两个典型例题引导学生进行得当的纵深、拓展和迁移，充分展现数学知识和数学思维的发生、发展过程？

下面就笔者的一堂市级公开课，从具体的操作过程着笔来谈谈本节课是否注意到了这点，望各位行家予以斧正．

授课班级：高三理科实验班4班；课型：第一轮复习；课题：函数的综合(3)——函数在给定区间上的极值、最值问题．

一开始用了约五分钟的时间对本节课所需知识进行了铺垫之后，再紧扣着一个典型例题予以展开．

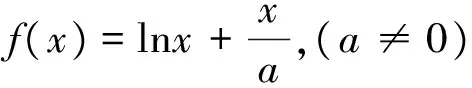
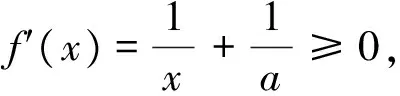
这是最基本的方法，当然要求同学们必须掌握．但做为核心素养的思维训练，仅限于此，显然是不够的．

与同学们共同完善了这种做法后，笔者有意地停顿了一会儿，并微笑审视着大家．

师：同学们还有没有什么别的想法？

短暂的思索，集聚了大家的思维指向，全体同学都陷入了思考与讨论之中．几分钟后，同学A站了起来．

生A：老师，我感觉还有更好的方法．

师：啊？你说说看？

该同学的思维过程如下：

最后，他很自信地说：“这样做就避免了前面常规解法中繁琐的讨论，而只考虑a>0的情况了”.

妙！！全班都报以了掌声．

规范化这种解法后，望着全班同学，笔者再次发出略带引发性的语言：“同学们，这种解法应该就是最理想的了吧？”

沉默了几秒后，孩子们又纷纷拿起笔开始了思考．很明显，大家都处于愤悱的情绪之中．抓住时机，巡视一圈后，见同学们没有什么理想的头绪，笔者继续引发．

师：要使函数f(x)取得最大值2，也就是对函数值有什么要求？

生A：函数值小于或等于2．

师(同时也在反问大家)：只要小于或等于2就行了吗？

很多同学频频点头．

师：我举一个例子，大家类比一下：要使我们班同学身高的最大值为2米，只须大家的身高小于或等于2米就可以了，对吗？

同学异口同声说：那不行，如果没有2米高的，就不算．哈，我们班也没有2米或2米以上的同学呀．

对！要的就是这句话．此时，部分同学有所感悟．

生B：对对对，应该说是值域为(—∞，2]，也就是f(x)的函数值要能取到2才行．

其他同学恍然大悟，频频点头．

短暂时间后，生C站了起来．

转化成了恒成立问题，妙！

生C：之后在(0,e]内分别求出左边的最大值及右边的最小值，并使得左边的最大值小于或等于右边的最小值就可以了．

师：非常好！那么，如何分别求出左右两边的最大、最小值？

约两分钟后，有的同学感觉到了麻烦．

生D：左边的最大值好求，因是增函数，但右边的最小值不好求，得就a的正负讨论才行，这样又麻烦起来了．更何况所给x的范围的左边是开区间．

师：分析得非常到位！现在看来，右边的最小值不好求，那我们可不可以换个角度去思考？

到此，所有同学也沉默了下来，不知道该如何进行下去……

生E(急不可待)：右边的图象是直线．对了，可以分别做出左右两边的图形，结合图形来考虑呀！

哈哈，一语道破，且思维还超前了一步．大家顿悟，纷纷画起了图形来．

师：对了，即使作出了左右两边函数所对应的图形，又能怎样？

生F：只要在(0，e]这个范围内，左边对应的图形在右边对应图形的下方就行．

师：好！那大家动手作图吧．

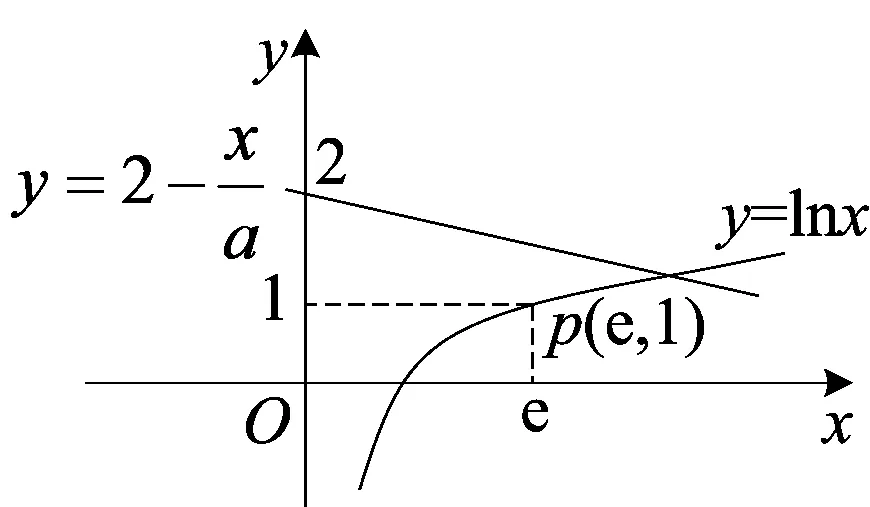
图1

师：很多同学作的图形，其右边的直线作得不准确．大家能观察到，右边是一条什么样的直线？

生G：是一条斜率不定的直线．

师：对．不过哈，大家也知道，动的东西，也

一定有定的因素！那么这条动直线有定的因素吗？

生H：对了，它恒过定点(0，2)！

妙！学生H上来黑板作出了如图1所示的图形，并作出了如下陈述．

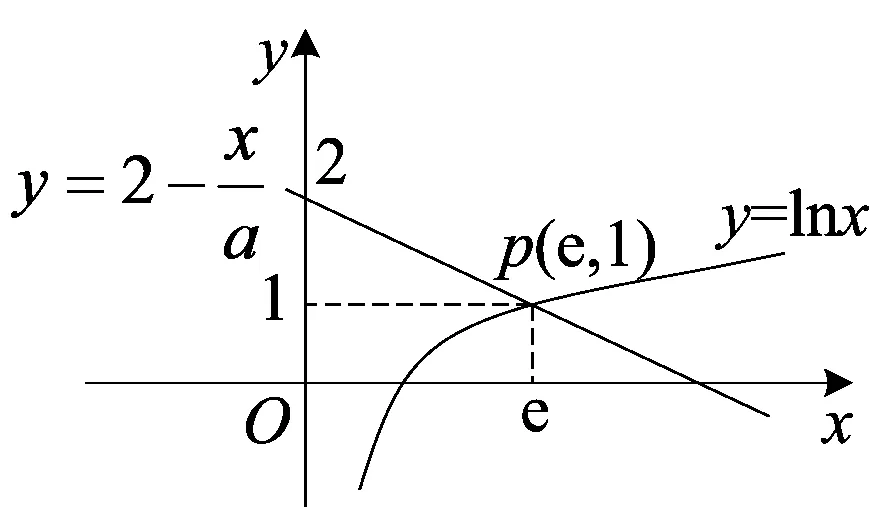
图2

师(环视全体)：有这个图，就行了吗？

生I：还要强调，在(0，e]内等号能够成立才行，直线必过点P(e，1)，不能上也不能下．

I同学上来将图1改成了图2所示的图象．

笔者充分赞扬了I同学，也规范化这种处理方法，并强调性地说明了图形对于解决数学问题的重要性．

经过如此强烈的思维过程后，很多同学都感觉有些累，同时也感受到了共同探索、积极思考所带来的惊喜．

而正当全体同学都有些疲惫也兴奋地在笔记本上记录上述思维过程时，又一位同学站了起来．

生J：老师，您看这样是不是可以．．．(还有些腼腆)先令导数等于0，就只有一个解x=-a， 所以在区间(0,e]上函数要有最大值为2，只可能在x=-a或在x= e处取得．如果 在x=-a处取得，-a必在(0,e]内，之后就能得出结论．

足足有两分钟之久，全班再次陷入沉思之中，很多同学都还没有反应过来．课堂的思维氛围又一次紧张起来！笔者的大脑也快速地运转了起来——毕竟，这是始料未及的事情．

师(对全体同学)：哈，同学J的思路是什么？你们听明白了吗？

部分同学：没有！

师：好，那请同学J上来给我们板书一下吧．

同学J的板书如下：

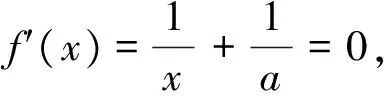
又x∈(0,e]时，f(x)要取得最大值为2，则只可能在x=-a或在x= e时取得．若在x=-a处取得最大值，-a必在(0,e]内．

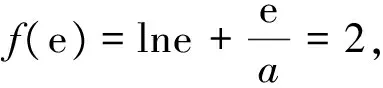
所以a∈φ，综上可知a=e．

太妙了！这样简洁明晰的思维，整个教室都再次响起雷鸣般的掌声…

本节课的最后，笔者也问了同样一个小结性的问题：本节课学到了什么？

好些同学纷纷畅谈到了自己在本节课中的收获：不仅仅是复习回顾了相关的数学知识，更重要的是数学思想方法与思维方式的得失，有的还提及到了能充分利用图象来处理的这一类题型的结构特征与思维规律．

现在，回想起前面说到的数学教育专家白涛教授提出的问题，本人的这堂高三复习公开课的具体授课过程，应该说也是或多或少地给以回答了吧？同时，也深感专家的这一问题，深蕴着多么深层的内涵！

我们的数学课堂，特别是高三的复习课堂，不只是一个传授知识的过程，更重要的是一个充分暴露知识的发生与发展、渗透数学思想、数学方法以及拓展学生思维的过程——这应该就是我们所说的培养学生学科核心素养的基本过程吧．