指向提升思维品质的数学教育

顾利国 娄洁

【摘要】本文论述数学教育应培养学生的思维品质，认为教师跳出“知识本位”观念束缚，站在“思维发展”的高点实施教学，通过编织知识体系培养思维的系统性，组织展示评价激发思维的批判性，设计拓展练习发展思维的深刻性，做到知识获取与思维发展融通合一。

【关键词】思维品质 融通合一 系统性 批判性 深刻性

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2018）12A-0111-02

学生学习的顺利度、思维水平的高低都与思维品质密切相关。指向思维品质提升的数学课，要求教师跳出“知识本位”观念的束缚，站在“思维发展”的高点来实施教学，努力做到“知识获取”和“思维发展”融通合一。

一、编织知识体系，培养思维的系统性

所谓编织知识系统，就是将碎片化、相对独立、零散的知识点进行“知识编码”，使之沟通整合成为相互连结、纵横交错却井然有序的“结构化知识”。一般情况下，教材在每个知识单元的最后，都会编排一个“整理与练习”;在整册教材的最后，编排“整理与复习”，其主要目的是帮助学生归类整理知识，构建知识网络。其实，课堂上学习的许多知识，都有“生长起点”和“发展方向”，教师应有意识地将知识体系的构建和完善落实到每一节课上，培养学生思维的系统性。

知识体系的构建过程，能很好地发展学生的系统性思维。系统性思维，不是就事论事，而是把相关的知识进行整体思考。这种思维方法，能让思考更具全面性、逻辑性、条理性，便于进行“板块化”认知，使得认知更为完整，更具穿透力，并使认知过程得到简化和优化。

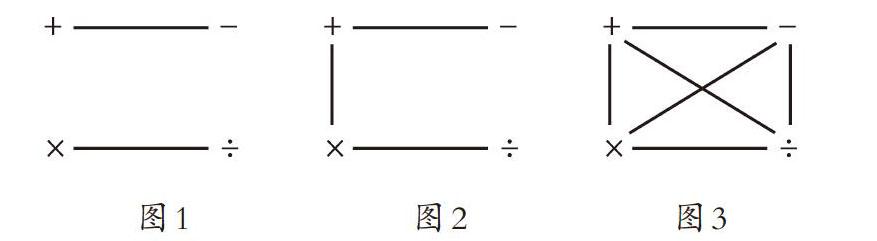
《乘法和加、减法混合运算》课始，教师以题组的形式（一组为连加、连减、加减混合式题;一组为连乘、连除、乘除混合式题）让学生口算，进一步复习“算式中只有加减法或乘除法，应按照从左往右的顺序计算”这一运算规则，完成板书（图1）。然后，以“12+2×5”激疑引出新课。

课尾，教学总结后，教师指着图1启发学生：以前，我们学习了算式中只有加减法或乘除法的混合运算，今天，又学习了算式中有乘法和加、减法的混合运算（将图1完善成图2），想一想，接下来我们还会学习哪种类型的混合运算呢？（根据学生的回答，把图2完善成图3）

三幅符号图，简单、清晰，笔墨不多，却是立意高远，起到四两拨千斤的效果。一方面，把“昨天”“今天”和“明天”的知识串成一个“知识组”，让学生知道知识是如何发芽抽枝拔叶的，是如何逐步生长的;另一方面，让学生的思维经历了时空“穿越”的过程，“瞻前顾后”“脉络清晰”“整体把握”等系统性思维得到有效培养。

二、组织展示评价，激发思维的批判性

展示评价是现行课堂常用的一种教学方式，一般是先让学生进行自主探究、自学、尝试，然后展示学习成果作品，同学之间相互发表各自的意见和看法，或赞同，或反对，或补充。这些作品来源于现实的课堂，来源于同伴，具有很强的真实感，学生参与评价的积极性很高。

因为学生之间的差异性，所以作品呈现出的资源比较丰富，能充分展现不同的思维路径和结果，有的正确，有的错误;有的似是而非，有的似非而是;有的异曲同工，有的独辟蹊径。这就要求学生积极思考，用心辨识。由此，在相互“揣摩”“认同”“否定”或“创造”的过程中，学生的批判性思维很容易被激发。

在教学《乘法和加、减法混合运算》一课“5×3+20”一式的运算顺序和书写规则后，教师让学生独立尝试解答“20+5×3”，然后展示代表性作品：

师：上面四个算式，你们认同哪一个？

生1：第一个。

师：为什么呢？说说你们对后面三个算式不认同的理由。

生2：……

在正例和反例的比对之下，在学生“真知灼见”“一针见血”的“批判”之下，做题错误的学生能充分认识到自己的错误并加以改正。在纠正错误的过程中，流淌着积极的批判性思维，一部分学生是在进行对他人的“批判”，另一部分是在自觉地进行自我“批判”，还有一部分学生是二者兼而有之。

三、设计拓展练习，发展思维的深刻性

拓展练习应该成为课堂教学的重要组成部分，通常以变式、反例、趣味性或加深思维力度的题型出现。它对拓宽知识面、发现知识的内在联系、提升思维含量，特别是发展思维的深刻性有着重要的意义。

思维的深刻性是一种透过现象看本质、分清事物实质的思维品质，其不仅表现出思维的深度，还表现出思维的广度、严密度和灵活度。数学教学，不能满足于基本知识的掌握和解答题目得出答案，还应该在此基础上加以拓展延伸，尽可能地把学生的思维引向广阔和深入。

在教学《乘法和加、减法混合运算》一课的练习中，教师出示了这样两道题：①39+12+12+12和②50-8-8-8-8-8。学生想到了简便计算：

师：刚才，我们是从“购物”的具体情境中发现了“算式中有乘法和加、减，应该先算乘法”这一条混合运算规律。现在，你能根据39+12+12+12=39+12×3这个式子来解释一下接下来为什么应该先算12×3，而不是先算39+12吗？

生1：因为12×3是表示3个12相加的整体，必须先算出整體。

师：那第二个算式为什么要先算8×5？

生2：8×5是表示5个8相加的整体，也要先算出整体。

是的，其实从具体情境中发现“算式中有乘法和加、减，应该先算乘法”这一运算规律，是牵强附会的，是刻意的人为设计，禁不起推敲和质疑。因为，只要换一个情境，完全可以得出“算式中有乘法和加、减，应该先算加、减法”这一规律。教师设计的拓展练习，不仅发展了学生思维的灵活性，还从“数学式”的本质让学生感受了“先算乘法”的合理性，让学生的思维走向理性。

总之，思维能力的发展关键在于不断改进思维的品质，思维品质的改善并不是一朝一夕能完成的，只有在教学中持之以恒，不断努力，才能真正提高学生的思维品质。

（责编 林 剑）