Spectral-spatial target detection based on data field modeling for hyperspectral data

Da LIU,Jianxun LI

School of Electronic,Information and Electrical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China

1.Introduction

With the development of imaging techniques,hyperspectral imaging instrument has already became a very important data source in many applications,including medical and health application,1Earth monitoring,2agriculture monitoring applications,3and military target detection.4,5

Usually,HyperSpectral Imagery(HSI)processing focuses on the analysis and recognition of spectral data collected by sensors.As is well known,the spectral data are widely used for ground truth classification and target detection.Several classic target detection algorithms for multispectral and hyperspectral data have been proposed,such as:(A)the detector based on the probability density model,including the Adaptive Coherence Estimator (ACE)6and constrained energy minimization(CEM)method.7ACE detector is essentially a Generalized Likelihood Ratio Test(GLRT)detector with a cone decision boundary.CEM obeys the criterion that target samples should have as intensive responses as possible while background samples should have as weak responses as possible;(B)the target detection approaches based on the geometric models,such as Orthogonal Subspace Projection(OSP)approach,7and Adaptive Subspace Detector(ASD).8OSP projects the spectral data onto an orthogonal subspace and restrains background samples by using a linear subspace model.ASD is a GLRT detector based on the linear mixture model,which achieves the target detection by estimating the abundance of the endmembers;(C)spectral matching detector,such as Spectral Angle Mapper(SAM)technique,9adaptive matched filter(AMF)10and the Kernel-Based Regularized-Angle Spectral Matching(KAR-SM)11algorithm.SAM identifies unknown spectral signatures by the similarity measurement to a prior known spectrum,which is another important kind of HSI target detection method.AMF is a further advance of the traditional spectral matched filter,and employs the estimated background clutter covariance matrix to describe the local statistics information.KAR-SM improves the spectral matching performance by introducing the kernel technique and regularized spectral angle.Moreover,some feature extraction techniques are employed for HSI target detection,typically the manifold embedding based approaches.The manifold embedding method is a nonlinear Dimensionality Reduction(DR)technology,which focuses on exploring the manifold embedded in the high-dimensional space by keeping some local properties.In Ref.12,13,two frameworks that unify different DR approaches,including their linearization,were proposed based on the manifold embedding idea.Typical manifold embedding target detection approaches including Manifold Embedding(ME)13detector,Unsupervised transfer learning based target detection(UTLD)14which is also named as Transfer Manifold Embedding(TME)in Ref.15,and Sparse Transfer Manifold Embedding(STME)technique.15TME detector preserves the discriminative information from training data to testing data which are not in the same feature space and with different data distributions by using a transfer regularization term.STME utilizes discriminative manifold embedding to extract spectral features and avoids the possible over-fitting in small sample size learning by introducing sparse and transfer constraints.

From the aspect of imaging mechanism,there should be a relationship between the spectral information and spatial information,because spatial neighbors always affect the measured signal by secondary illumination in HSI.The adjacency effects caused by surface reflection and atmospheric scattering have been shown in Ref.16.Several spectral-spatial classification methods17–19for HSI have been proposed.The spectral features and spatial features are actually extracted and processed independently in these methods.A drawback of these approaches is that the spectral features and spatial features are measured in different scales.Hence,the spectral and spatial features are usually simply stacked.Moreover,the spatial information extraction always relies on rich prior image information and image segment,which are difficult to be achieved in target detection application.A Data Field based Support Vector Detector(DFSVD)20was proposed to achieve the spectral-spatial target detection for HSIs.Based on the data field modeling,the spectral information and spatial information are fused as data field potential.Then,a hyper-sphere with higher potential for target detection is determined by using the support vectors.However,the spatialk-NNs in DFSVD are simply regarded as unit charges,which may make the spatial information lost.Besides,the charge characteristic of the spatialk-NNs is mutually set according to target types,which may also bring errors to target detection results.Another data field based method for HSI classification was proposed in Ref.21.The classification method in Ref.21fused the spectral and spatial features based on a linear fusion model.It should be noted that the weight coefficient can be effectively learned and describe the inner connection between spectral and spatial features due to the rich label information.

In this paper,a spectral-spatial hyperspectral target detection method on the basis of data field theory is proposed.The spectral information and spatial information are unified as radiation features in the data field modeling in both the spectral space and image spatial space.Then,local information is introduced to the discriminative manifold embedding in order to explore the discriminative information for target detection which lies in the decision boundary and emphasize the samples located in the boundary margins.Hence,the two data fields are fused and the most discriminative features that contain both spectral and spatial information are extracted.The performance of the presented target detection algorithm is demonstrated by three widely used HSI test datasets.Different from the data field based classification method in Ref.21which trained a weight coefficient,the target detection algorithm in this paper aims to train an optimal transfer matrix,which can be seen as a structure feature of the target samples in the data field modeling.

This paper is organized as follows:Section 2 presents the proposed data field modeling approach in HSI.Section 3 proposes the feature extraction method inspired by manifold learning idea with the data field modeling.In Section 4,the experimental results on three HSI test datasets are analyzed and illustrated.Furthermore,the determining method and the influence of the key parameters on the algorithm performance are discussed in this section.The contributions of this study are presented and conclusions are drawn in Section 5.

2.Data field modeling

In this paper,we first unify the spatial information and spectral information by the introduction of data fields.In order to apply the field theory in physics to mathematical modeling,data field was proposed and used for simulating the physical field.In a data field,data always interacted with each other.Due to the data interaction,according to the data field idea,the property of a data point in data fields is jointly determined by itself and the data interacted with it.For the purpose to describe the data interaction in data fields,data can be considered as radiation sources and the radiation effects between the data can be seen as the descriptions of the data interactions.In this study,data field theory is employed for the data modeling in HSIs.Thus,the identification for a test pixel is not merely dependent on its own reflectance spectra signatures,but also the relationships with other pixels in the HSI.

By prior knowledge,a training sample set can be obtained which consists of two parts:a positive training set denoted by｛xi｝i=1，2，...，Niand a negative training set denoted by ｛xl｝l=1，2，...，Nl.In the paper,positive samples are represented by subscriptiand negative samples are denoted byl.Further,N=Ni+Nldenotes the size of the training set,whereNiandNldenote the positive sample number and the negative sample number,respectively.In this paper,for the purpose of data field modeling in HSI,several rules are proposed as follows:

Rule 1.Both the spectral domain and the image domain are considered as data fields.Thus a pixel in HSI receives radiation from its Nearest Neighbors(NNs)in both the HSI spectral data field and image spatial data field.

Rule 2.Generally,the pixels in thek-neighborhood of a given pixel are called as itsk-nearest neighbors(k-NNs).In this paper,a data point receives radiation from itsk-NNs in the image spatial domain,which are called as spatial NNs in the following.

Rule 3.Similarly,in the spectral domain data field,a data point interacts with itsk-NNs in the positive training set｛xi｝i=1，2，...，Niby the radiation effects,which are called as spectral NNs.

In the following,the spectral NNs and spatial NNs are termed as Surrounding Radiation Samples(SRSs)for simplicity.As mentioned above,data interact with each other though the radiation effects in data fields.In order to establish the data field radiation,radiation function is defined as follows,which gives the mathematical representation for data radiation:

whereorepresents a datum in data fields,rdenotes the distance too,Eis the radiation intensity at distancer,ρ is a radiation factor andv（o）indicates the initial energy.In this paper,the Euclidean distance is employed as the distance measurements.On the basis of the concepts and rules proposed above,data field modeling operation can be implemented on HSI.According to data field modeling rules in HSI,a given sample in HSI receives the radiation effects from the spectral NNs and spatial NNs.Using the radiations from all the SRS,we unify the spectral and spatial information via stacking these radiations together.Therefore,a sample point xiis projected to eiwhich is called as Data Field Radiation Feature(DFRF):

whereN1andN2are the numbers of the spectral NNs and spatial NNs,respectively.is the radiation caused by thejth spectral NNs.is the energy radiated from thejth spatial NNs.We de fine:

3.Feature extraction

Based on the data field modeling,the spectral information and spatial information are unified as DFRF.As mentioned above,there should be a fixed local structure,in another word,a feature,to describe the spectral and spatial feature of the targets.In this section,we use manifold embedding technique to extract he most discriminative features in DFRF.

For a positive training sample xi,we first build the local patch.Thek1-NN with respect to xifrom positive training set is selected,denoted byThen,we select the

Furthermore,considering all the training sample patches,we sum the patch optimizations to obtain the whole optimization:

As well known,this optimization problem can be solved by introducing Lagrangian multiplier.The optimal solution of Q can be obtained by conducting the generalized or standard eigenvalue decomposition.It should be emphasized that,in the view of feature extraction,Q represents the data structure features of the target samples.In the data field aspect,Q is an initial data energy matrix of the SRS,and it describes the interactions between the target samples and the SRS.Thus,Q can be seen as a description of the adjacency effects in the HSI domain.In Eq.(13)and Eq.(14),it should be noted that all the training sample patches are regarded as having the same importance in the feature extraction process,and the Q learned by Eq.(14)achieves a global optimization.However,the boundary information is ignored.In this paper,in order to extract more discriminative features to achieve superior target detection performance,the local information is introduced to explore the discriminative information for target description and detection which lies in the decision boundary and emphasize the samples which locate in boundary margins.By the introduction of local information,the boundary points are emphasized.For a given training sample xi,we define a coefficient ωito describe the local information:

whereG=The features are extracted by our weighted manifold embedding method based on data field modeling,so we call this method as Data Field Weight Manifold Embedding(DFWME).Finally,the extracted features are processed by a NNs detector.For a test pixel,its detection result is scored by sorting the NNs of feature vectors of the training samples in the feature space.For example,an extracted feature of a test pixel z by DFWME is y=QTe（z）,and the corresponding DFWME feature sets of the positive and negative training sets are respectively represented as

Then,｛yj｝j=1，2，...，Ni+Nlare sorted in a NNs manner according to y,i.e.,the first term in the sorted list is the nearest neighbor of y.The target detection result of the test pixel z is the number of the DFWME features belonging to ｛yi｝i=1，2，...，Niin the firstNinearest neighbors in the sorted NNs list.

Fig.1 shows the DFWME algorithm flowchart for HSI target detection.As shown in Fig.1,the data field modeling operations are implanted in both the spectral space and the image spatial domain.Then the DFRF is built.The feature extraction based on the manifold embedding technique with local information is then performed.The transfer matrix Q is learned in this step.Hence,the DFRFs are projected into a low-dimensional feature space which contains the most discriminative features.For a test sample,the DFRF which contains both the spectral information and spatial information is first built.Then,the feature extraction is implemented by using the DFRF and transfer matrix Q.Consequently,the target detection map is obtained by processing the extracted features with NNs detector.

4.Experiments and results

In this section,a hyperspectral self-test dataset captured by a HyMap airborne hyperspectral sensor,an Airborne Visible/infrared Imaging Spectrometer(AVIRIS)hyperspectral dataset and a hyperspectral dataset acquired on the city of Pavia,Italy by the reflective Optics Spectrographic Imaging System(ROSIS-03)are employed to test the algorithm efficacy.Firstly,the descriptions of the hyperspectral datasets acquired by different hyperspectral imaging instruments in the experiments are presented.Secondly,the experimental settings are given.Then,the analysis and discussion of the target detection results on both synthetic targets and real targets are drawn.Finally,the important parameters used in DFWME algorithm are analyzed.

4.1.Dataset description

The first target detection test case was carried out on a selftest dataset provided by the Rochester Institute of Technology.22This well-known dataset was captured on Cook City,MT,USA in 2006.The image consists of 280×800 pixels and provides 126 spectrum bands.The spatial resolution of this dataset is about 3 m/pixel,and the spectral resolution is 14 nm approximately.In this test case,a number of synthetic targets using different implant fractions were implanted into the dataset.Both real target and implanted target pixels are to be detected.As shown in Fig.2(a),the locations of the real fabric targets(F1-F4)and vehicle targets(V1-V3)are highlighted in the test dataset.The ground truth pictures of target sF3 and V3 are shown in Fig.2(b)and (c),respectively.

Fig.1 Flowchart of DFWME algorithm.

Fig.2 False color image and detailed real targets of self-test dataset.

The second hyperspectral dataset was collected by an AVIRIS from Moffett Field,CA,USA.The spatial resolution is about 3.3 m/pixel and the spectral resolution is nearly 10 nm.A total of 224 spectral bands ranging from 365 to 2500 nm,including the water absorption bands in 1313–1422 nm and 1811–1937 nm,are taken into consideration.Hence,200 data channels were used after the spectrum bands removal operation.There are two planes(in the red marked region)desired to be detected in the dataset as shown in Fig.3(a).

The ROSIS-03 dataset was called as University of Pavia dataset which was acquired on the city of Pavia,Italy.University of Pavia dataset is composed of 115 bands of 610×340 pixels.Different from the other two datasets,this test dataset provides the highest spatial resolution with 1.3 m/pixel.The 102 spectral channels out of 115 were processed due to noise.The metal sheet region is desired to be detected as show in Fig.3(b).

4.2.Experimental setting

In allthe experiments on different datasets,we setN1=N2=8 andd= （N1+N2）/2.In the self-test dataset,the V3 and F3 are the real targets to be detected.Moreover,a number of synthetic targets with different implant factors were also implanted into the dataset.The self-test dataset was employed to demonstrate the performance of DFWME in pixel/subpixel target detection problem.

The AVIRIS and ROSIS-03 datasets were applied to validate the algorithm performance in area target detection problem.Two airplanes and a metal sheet roof are desired to be detected.In all these experiments,the detection images in our proposed method were given.Furthermore,as a widely used metric for evaluating the performance of detection approaches,Receiver Operating Characteristic(ROC)curve was employed to assess the detection performance of the pro-posed method against the reference detecting approaches.Obviously,the algorithm with the best performance should have a curve nearest to the(0,1)point,which indicates the highest detection probability under the smallest False Alarm Rate(FAR).Moreover,FARs under 100%detection were employed to validate the effectiveness of the parameters.

Fig.3 RGB images of AVIRIS and ROSIS-03 datasets.

The conventional hyperspectral detection methods:ACE,ASD,KAR-SM,ME,TME,STME and DFSVD were used for comparison.ACE and ASD are classic hyperspectral target detection methods based on the traditional probabilistic model and geometric model,respectively.KAR-SM is a state-of the art spectral matching filter.ME,TME and STME are representative manifold embedding approaches,and DFSVD is a HSI target detection algorithm based on the data field theory.In our experiments,ME,TME and STME extracted the same number of features with DFWME,i.e.,d=8.

For the traditional hyperspectral target detection approaches ACE,ASD and KAR-SM,a prior known target spectrum was used as prior information.For DFWME,ME,TME,STME and DFSVD,we usedn-fold cross-validation withn=10 to evaluate the target detection performance.Ten percent of the target samples and the same number of samples randomly selected from background are used for training.The rest samples are used for evaluation.This process is repeated ten times.

4.3.Experimental results

4.3.1.Experiments with self-test dataset

The self-test dataset provided by Rochester Institute of Technology is a standard dataset which is always used for target detection algorithm performance evaluation.There are three vehicle targets(V1-V3)and four fabric targets(F1-F4)located in the image scene.The specific locations and spectral signatures of the targets are provided in the Region of Interest(ROI)files and SPectral Library(SPL)files respectively.A number of ground object classes,such as roofs,vegetation,roads,and bare soil,can be seen in this self-test dataset.The target spectra and the representative spectra of the background classes are displayed in Fig.4.

For the purpose of evaluating the target detection performance in a wide range for particular targets,the target implant method suggested in Ref.15,23,24was used,and then a number of synthetic targets with mixture spectral signatures using different implant fractions were implanted in the scene.It can be observed in Fig.5 that 100 synthetic subpixel targets were implanted in the subimages which consist of 200×200 pixels and include targets V3 and F3,respectively.It should be noted that the spectra of the implanted targets in different columns were generated by fractionally implanting the corresponding real target spectra in the located pixels with different implant factors.In this test case,the implant factorsfare in the range from 0.9 to 0.45 with interval 0.05.

The target detection resulting images of V3 and F3 with the proposed DFWME and compared methods are shown in Figs.6 and 7,respectively.Besides,the ROC curves of the reference approaches and our method are given in Fig.8.

Fig.4 Target spectra and typical background spectra.

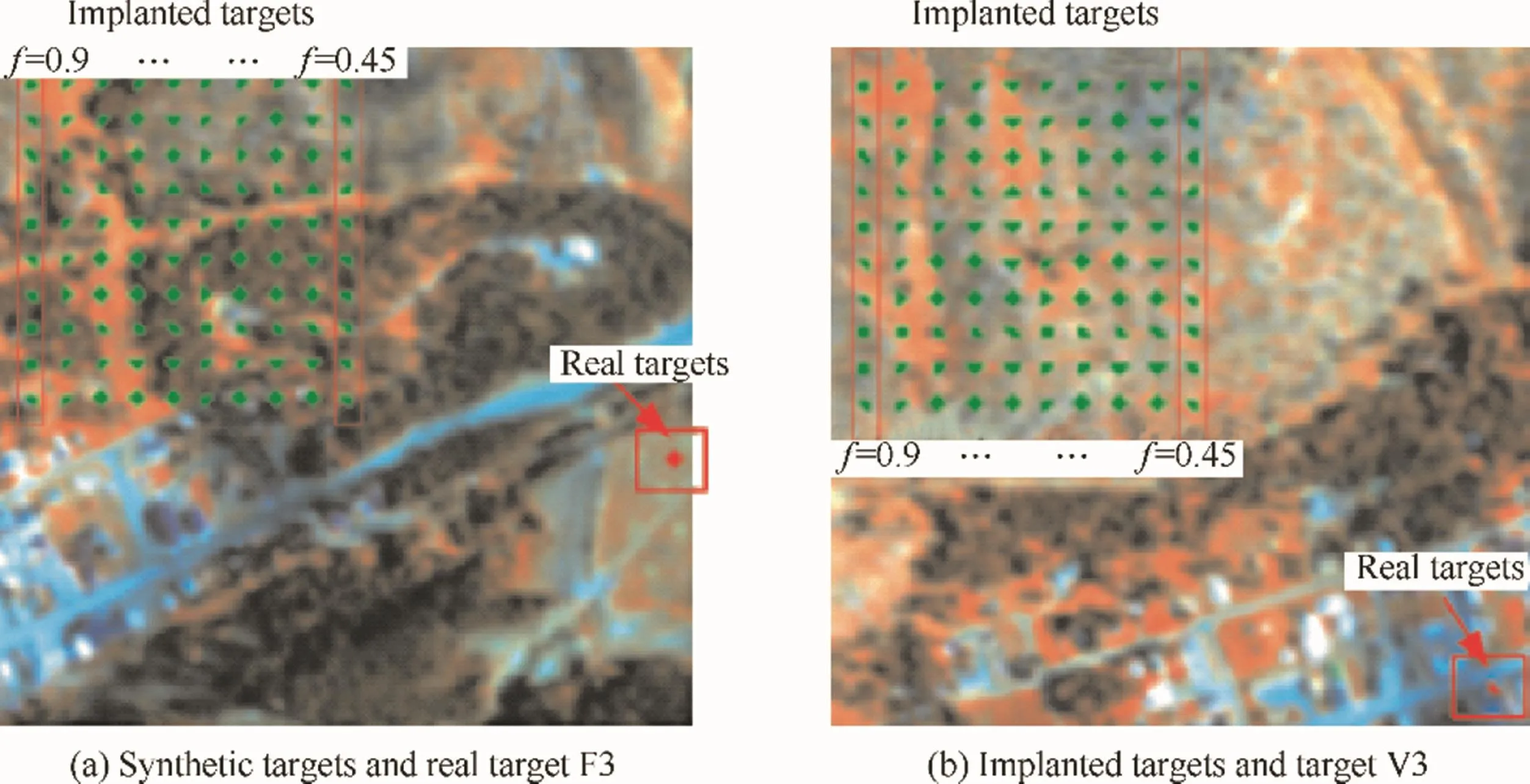
Fig.5 RGB subimages.

Fig.6 Target detection results of real targets(marked with red boxes F3)and implanted synthetic targets with DFWME and compared methods.

Fig.7 Target detection results of real targets(marked with red boxes V3)and implanted synthetic targets with DFWME and compared methods.

Fig.8 ROC curves of F3 and V3.

The ROC curves indicate superior detection performance of our method compared to the reference methods.DFWME obtained higher detection probabilities with lower FARs.In the F3 target detection problem,DFWME showed superior target detection performance compared to the reference approaches with an approximate 2.2×10-3FAR under 100%detection.In the V3 scenario,DFWME achieved the best target detection result with a FAR lower than 1×10-4under 100%detection.Two main reasons could explain this superior performance in detection.(A)The data field modeling technique unifies the spectral information and spatial information into a DFRF.The introduction of the spatial information improves the distinction between the target class and backgrounds,which further improves the detection algorithm performance.(B)The local information was introduced into the manifold embedding.The local information emphasizes the contribution of the boundary points to the feature extraction,which effectively enhances the separability between the background class and the target class in the feature space.

As shown in Fig.8,DFSVD reported better detection results than the other hyperspectral target detection approaches.This is because DFSVD detector considers both the spectral and spatial information for target detection by introducing the data field theory.Compared with DFSVD,DFWME trained the data energy of all the SRS,and the boundary information was emphasized by using the local information.Thus,more spatial information was introduced than DFSVD,and the target detection was improved effectively.In this self-test dataset,the synthetic targets were implanted into the images with implant factors from 0.9 to 0.45.Thus,ACE,ASD and KAR-SM algorithms which are always used for specific target spectra detection are vulnerable and unreliable in this target detection case due to the high spectral variability.It can be seen from Fig.8 that the performance of ACE,ASD and KAR-SM is influenced by the spectral signature discrimination between the targets and backgrounds.ACE,ASD and KAR-SM hence performed much better in the target F3 detection problem.According to the ROCs reported in Fig.8,ACE shows better detection results than ASD and KAR-SM.This is because ACE uses a cone decision plane to detect targets,which is more robust to the spectral variability than ASD and KAR-SM.The manifold embedding techniques learn a subspace(or feature space)embedding in the ambient high-dimensional space,which aims to separate the target class from the background classes as far as possible in the feature space on the basis of the prior information.It should be noted that STME always achieves relatively satisfactory target detection performance in comparison with ME and TME.TME performs better than the original ME algorithm,because the introduction of the transfer regularization effectively preserves the dominant structure of the training data,which transfer the extracted feature from the training samples to the test samples.STME further uses the sparse constrains to avoid the over-fitting problem,which further improves the target detection performance.

4.3.2.Experiments with AVIRIS and ROSIS-03 dataset

The second dataset is an AVIRIS dataset.As stated above,200 spectral channels are taken into consideration after the water absorption bands removal operation.In the second test case,the two airplanes in the scene are the targets to be detected as shown in Fig.3(a).The reflectance spectra of both airplane targets and typical background in this dataset are displayed in Fig.9(a).In this test case,the two airplanes in the scene are two challenging small targets.Different from the other two datasets,targets in this test case are neither typical point small targets nor area targets which have contextual features and cover a large region.This dataset is used to validate the target detection performance of the proposed method in this situation.

The ROSIS-03 Pavia University dataset is a typical target detection problem in urban scene.In this test case,dataset provides both high spectral resolution and spatial resolution.The target in this dataset is an area target,and the detailed target location is provided in Fig.3(b).Fig.9(b)gives the target spectral signature and representative background spectrum in this scene.The main challenge in this experiment is that the background is complex in this scene,and some background classes are spectrally similar to the target pixels.

The detection images of the two datasets are shown in Figs.10 and 11,respectively.The ROC curves of the proposed approach and the reference algorithms are shown in Fig.12.It can be observed from these ROC statistical curves that DFWME gives a more distinguishable detection result than the traditional hyperspectral target detection approaches.The ROC curves demonstrate superior detection performance in comparison with the other spectral target detection methods by restraining false alarm effectively without losing detecting probability.It demonstrates that data field modeling and introducing local information in manifold embedding improve the detection algorithm performance remarkably.

Fig.9 Target and background class spectral signatures.

Fig.10 Detection results for AVIRIS dataset with different algorithms.

Fig.11 Detection results for ROSIS-03 dataset with different algorithms.

The detailed detection performance analysis can be given based on the ROC curves.Both of the experiments in the two datasets demonstrate that our method achieves superior performance compared to reference approaches.The FARs under 100%detection in the AVIRIS and ROSIS-03 datasets are 1.53×10-4and 2.58×10-4,respectively.DFWME always achieves a lower FAR under 100%detection compared to the reference approaches.Compared to the ACE,ASD,KAR-SM and manifold techniques,the advantage of DFWME is the introduction of the spatial information by data field modeling.It should be emphasized that DFSVD,KAR-SM and STME achieved excellent detection performance.However,the proposed method further improved the target detection performance.In comparison with STME,DFWME introduced the spatial information and local information,which jointly contribute to the target detection.As shown in Fig.12,KARSM performed well in these two datasets.The reason behind this should be that KAR-SM detector is a spectral matching filter and generally used for pure pixel targets detection scenario,and the targets in these two datasets are area targets,which is a typical pure pixel target detection problem.Compared to KAR-SM,the data field modeling can unify the distinctive spectral and spatial information.Then,the most discriminative features were extracted by the weighted manifold embedding.Hence,DFWME achieved better target detection performance than KAR-SM.In these two datasets,DFWME improved the target detection performance effectively compared with DFSVD approach,particularly in the AVIRIS datasets.The FAR sunder100%detection decrease by70.58% and 61.89%in AVIRIS and ROSIS-03 datasets,respectively.Beyond more spatial information that was introduced,another reason is that the initial data energy of the spatial nearest neighbor was determined adaptively without manual setting,which avoids the errors brought by the target types.Thus,DFWME achieved higher target detection probability with lower FAR than DFSVD.

Fig.12 ROC curves of two different dataset.

Finally,the computational complexity of the proposed target detection algorithm was given.As an example,the processing time(or operation time)of the algorithms was compared on the AVIRIS dataset as shown in Table 1.The experiments were carried out in MATLAB environment under Intel Core i5 CPU with 3.2 GHz and 4 GB RAM.As can be seen in Table 1 that,compared to other methods,DFWME target detection approach achieved superior target detection performance at the cost of greater computational complexity and time consumption.However,the speed of our method could be improved by using time-efficient feature extraction approaches and parallel computing techniques.

4.4.Parameters

In the proposed DFWME target detection algorithm,the accuracy of the data field modeling which depends on the radiation factor and the number of NNs determines the algorithm performance.Thus,these two parameters are discussed in this section.

Table 1 Processing time for AVIRIS dataset.

It can be seen from Eq.(1)that radiation function describes the data interaction in data fields and the radiation factor determines the data radiation range.In data field modeling,the intensity of the radiation indicates the relationship and effects between data pairs.The data radiation could be meaningless if the radiation factor was selected in an inappropriate way.For example,the radiation could always be ignored when the radiation factor ρ is extremely large,whereas the radiation between all the data pairs could be always very large when ρ is too small.In this section,we used the training set to adaptively determine the radiation factor.For a given positive training set,the mean vector of the positive set is denoted by,which could be considered as the center of the target class.It is desired that the samples in the positive training set and the negative training set have as possible as strong and weak radiations to,respectively,i.e.,

The solution can be expressed as

wherer+indicates the mean distances between positive samples and the class centerr（xi）,i=1，2，...，Ni,andr-is the mean value of the distances between the negative samples and the class centerr（xl，）,l=1，2，...，Nl.Therefore,radiation factor ρ can be obtained by the training samples according to Eq.(17).

In the DFWME approach,the number of NNs,N1andN2,determines the target detection performance.The more NNs were considered in the data field modeling,the more accurate the data interactions in the data field are and the more data in HSI the target detection for a pixel is supported by.As shown in Fig.11,The influence of the number of NNs on the performance of algorithm was demonstrated by the FARs under 100%detection.It should be emphasized that we always set the same number forN1andN2in this study.As shown in Fig.13,the FARs decrease as the number of NNs increases.Thus,it can be concluded that a large number of NNs contribute positively to the algorithm performance because of a more accurate data field modeling.Furthermore,it should be noted that there is an inflection point atN1=N2=8 in the experimental results with all the datasets in Fig.11.On the other hand,it should be noticed that more NNs bring higher dimensionality of DFRF,which may lead to higher computing cost.Thus,it is reasonable to setN1=N2=8 in our experi-ments,which considers both the target detection performance and the computing cost.

Fig.13 Variation of FARs of DFWME under 100%detection with different numbers of NNs(N1=N2).

5.Conclusions

In this study,a spectral-spatial feature extraction algorithm based on data field theory and manifold embedding technique was proposed for target detection in HSI.As a mathematical realization of field theory concepts in physics,data field theory was employed to establish data field modeling in HSI.Both the spectral domain and spatial domain were considered as data fields.According to the data filed modeling,the DFRF was built and feature extraction based on the manifold embedding technique with local information was then performed.The transfer matrix training procedure was essentially a feature extraction process.It should be emphasized that,in the view of feature extraction,the transfer matrix represents the target structure features,which contains both spectral signatures and spatial information.From the perspective of data field,transfer matrix describes the interactions between the target samples and the SRS.Thus,the transfer matrix can be seen as a description of the adjacency effects in the HSI domain.The spectral-spatial target detection was achieved and the relationship between the spectral and spatial information was explored by learning the transfer matrix.According to the experiments on three different test datasets,it is shown that the method achieves improved target detection performance.

1.Liu HY,Li QL,Xu L,Wang YT,Liu JG,XUE YQ,et al.Evaluation of erythropoietin efficacy on diabetic retinopathy based on molecular hyperspectral imaging(MHSI)system.J Infrared Millim Waves2012;31(3):248–53.

2.Andrew ME,Ustin SL.The role of environmental context in mapping invasive plants with hyperspectral image data.Remote Sens Environ2008;112(12):4301–17.

3.Bannari A,Pacheco A,Staenz K,Mcnairn H,Omari K.Estimating and mapping crop residues cover on agricultural lands using hyperspectral and IKONOS data.Remote Sens Environ2006;104(4):447–59.

4.Manolakis D,Siracusa C,Shaw G.Hyperspectral subpixel target detection using the linear mixing model.IEEE Trans Geosci Remote Sens2001;39(7):1392–409.

5.Manolakis D,Shaw G.Detection algorithms for hyperspectral imaging applications.IEEE Signal Process Mag2002;19(1):29–43.

6.Kraut S,Scharf LL,McWhorter LT.Adaptive subspace detectors.IEEE Trans Sig Process2001;49(1):1–16.

7.Harsanyi JC,Farrand WH,Chang CI.Detection of subpixel signatures in hyperspectral image sequence.Proceedings of the American society for photo gramme try and remote sensing;1994.p.236–47.

8.Kraut S,Scharf LL.The CFAR adaptive subspace detector is a scale-invariant GLRT.IEEETransSigProcess1999;47(9):2538–41.

9.Richards JA.Remote sensing digital image analysis:an introduction.Berlin:Springer;1999.p.47–54.

10.Robey FC,Fuhrmann DR,Kelly EJ.A CFAR adaptive matched filter detector.IEEETransAerospElectronSyst1992;28(1):208–16.

11.Gu Y,Wang C,Wang S,Zhang Y.Kernel-based regularized-angle spectral matching for target detection in hyperspectral imagery.Pattern Recogn Lett2011;32(2):114–9.

12.Yan SC,Xu D,Zhang BY,Zhang HJ,Yang Q,Lin S.Graph embedding and extension:a general framework for dimensionality reduction.IEEE Trans Pattern Anal Mach Intell2006;29(1):40–51.

13.Zhang T,Tao D,Li X,Yang J.Patch alignment for dimensionality reduction.IEEE Trans Knowl Data Eng2009;21(9):1299–313.

14.Du B,Zhang L,Tao D,Zhang D.Unsupervised transfer learning for target detection from hyperspectral images.Neurocomputing2013;120(10):72–82.

15.Zhang L,Zhang L,Tao D,Huang X.Sparse transfer manifold embedding for hyperspectral target detection.IEEE Trans Geosci Remote Sens2014;52(2):1030–43.

16.Tanre´D,Deschamps PY,Duhaut P,Herman M.Adjacency effect produced by the atmospheric scattering in thematic mapper data.J Geophys Res1987;92(92):12000–6.

17.Borhani M,Ghassemian H.Hyperspectral image classification based on spectral-spatial features using probabilistic SVM and locally weighted Markov random fields.IEEE intelligent systems;2014 February 4–6;Piscataway:IEEE Press;2014.p.1–6.

18.Fauvel M,Tarabalka Y,Benediktsson JA,Chanussot J,Tilton JC.Advances in spectral-spatial classification of hyperspectral images.Proc IEEE2013;101(3):652–75.

19.Ji RR,Gao Y,Hong RC,Liu Q,Tao DC,Li XL.Spectral-spatial constraint hyperspectral image classification.IEEE Trans Geosci Remote Sens2014;52(3):1811–24.

20.Liu D,Li J.Data field modeling and data description for hyperspectral target detection.J Appl Remote Sens2016;10(3):035001.

21.Liu D,Li JX.Data field modeling and spectral-spatial feature fusion for hyperspectral data classification.Sensors2016;16(12):1–16.

22.Snyder D,Kerekes J,Fairweather I,Crabtree R,Shive J,Hager S.Development of a web-based application to evaluate target finding algorithms.IEEE geoscience and remote sensing symposium;2008 July 7–11;Piscataway:IEEE Press.2008.p.915–8.

23.Tilton JC,Tarabalka Y,Montesano PM,Gofman E.Best merge region-growing segmentation with integrated nonadjacent region object aggregation.IEEE Trans Geosci Remote Sens2012;50(11):4454–67.

24.Luo H,Tang YY,Yang L.Incorporating local and global geometric structure for hyperspectral image classification.IEEE international conference on systems,man and dybernetics;2014 December 7;Piscataway:IEEE Press;2014.p.4092–6.