Time-varying linear control for tiltrotor aircraft

Jing ZHANG,Liguo SUN,*,Xingju QU,Liuping WANG

1.Introduction

A tiltrotor aircraft,which combines the characteristics of helicopters and fixed-wing aircraft,consists of an aircraft body(including the fuselage and wings),engine nacelles,and rotors.Unlike a traditional aircraft,a tiltrotor aircraft is a complex multibody system which can change its configuration by tilting the nacelles,and it owns three different flight modes,namely helicopter mode,airplane mode,and transition mode.The transition mode,which means the conversion between the other two flight modes,is a special mode of tiltrotors.A tiltrotor aircraft with two side-by-side rotors such as the XV-15 tiltrotor is studied in this paper.

A tiltrotor owns the advantages of both helicopters and fixed-wing aircraft.Firstly,a tiltrotor can fly freely in different directions like a helicopter,and can also hover in the air.Secondly,a tiltrotor has a faster cruising speed than that of a helicopter.Thirdly,a tiltrotor can enhance civil or military transportation capability because it has three flight modes.However,a tiltrotor aircraft has some disadvantages such as low safety and low reliability.Firstly,the flight dynamics of a tiltrotor is much more complex than that of a traditional aircraft since the tiltrotor demonstrates different flight dynamic characteristics in different flight modes,and there exist inertial couplings between the aircraft body and nacelles.Secondly,a tiltrotor has low reliability because there are control couplings between its control action paths.Thirdly,the pilot workload of a tiltrotor would be higher especially in the transition period,because it has the characteristics of complex flight dynamics,inertial couplings,and control couplings.This paper studies the flight control for tiltrotor aircraft to deal with the complex flight dynamics and inertial couplings.

To obtain a reasonable and reliable dynamic model is crucial for aircraft controller design.A large amount of literature considers a tiltrotor as a single rigid body,and describes its dynamic characteristics through three-Degree-Of-Freedom(DOF)longitudinal modeling or six-DOF modeling,which is similar to that for traditional aircraft.1–3However,a tiltrotor is a kind of morphing aircraft which tilts its nacelles in its special transition mode,so a traditional flight dynamic model cannot reveal the inertial couplings and dynamic characteristics in the transition mode.Certain literature regards a tiltrotor as a multi-rigid-body system in view of the inertial couplings.For example,Li et al.considered a tiltrotor as multiple entities,and developed a twelve-DOF dynamic model for tiltrotors based on multibody dynamics.4The multibody model can clearly characterize the inertial couplings and complex flight dynamics of a tiltrotor,but its expression is too complicated for controller design.Later on,based on the Lagrange’s equation,Zhang et al.built a multibody longitudinal nonlinear model of a tiltrotor,and the derived model is in a more concise form and more suitable for the longitudinal controller design of the tiltrotor.5It is worth noting that modeling of multibody systems has experienced a remarkable development in space flight.6,7Furthermore,founding an aeroelastic model is beneficial to analyzing the stability of the tiltrotor.8

The literature about tiltrotor aircraft control can be classified into two categories:linear control and nonlinear control.Firstly,linear controllers were designed on the basis of a linear dynamic model and the information of certain flight conditions,and references are organized chronologically.A Model Predictive Control(MPC)method was adopted to design a flight controller for the hovering mode and three other typical flight scenarios of a tiltrotor.9An attitude controller for a tiltrotor in the helicopter hovering mode was designed using MPC.10An optimal control approach was proposed to deal with gusts effects on a tiltrotor in helicopter and airplane modes.11Minimum energy controllers were designed based on the helicopter mode and the airplane mode,respectively.12Based on optimal preview control,an attitude controller was developed for a particular flight state in the transition mode of a tiltrotor.13In consideration of model errors,a controller was designed for the airplane mode of a tiltrotor based on a sliding mode method.14It should be noted that the above mentioned linear controllers were mainly designed for one or several particular flight states of a tiltrotor,and they need gain scheduling to achieve control of the whole conversion process of the tiltrotor.Secondly,nonlinear control approaches have the advantage that the nacelle angle does not need to be assumed fixed when designing tiltrotor flight controllers.In Ref.15,a robust nonlinear controller was designed for a tiltrotor in the hover mode.Considering system uncertainties and disturbances,an adaptive control method was developed based on Neural Networks(NNs),16but it requires using different NN weights for different flight states,e.g.,different nacelle angles.Based on the work,16an online NN modelling method was introduced to develop a fully adaptive flight control method,which achieves not only longitudinal control but also lateral control of a tiltrotor.It should be mentioned that this method needs to update the entire full-state nonlinear model of a tiltrotor for different flight states.17Considering the control difficulty brought by the tiltrotor mode switching process and the tiltrotor configuration change during the transition mode,Ref.18presented a nonlinear control method and specifically studied the transition process control.Nevertheless,the tiltrotor controller designed in Ref.18fails to consider input constraints and control couplings.

A tiltrotor aircraft,especially in the transition mode,is a time-varying and strongly nonlinear system,and there exist couplings between different control action paths.As an alternative to linear controllers with a gain scheduling mechanism and nonlinear controllers mentioned above,it is a wise choice to convert a time-varying highly nonlinear system into a Time-Varying Linear(TVL)system,and then design a controller based on the TVL model.There exist a large number of approaches in literature considering founding a TVL model and TVL control.19–22The Linear Parameter Varying(LPV)control method,which approximates a nonlinear system as a TVL system,is a classical control method which has been widely applied to aircraft with a variable structure.23–27However,a single LPV controller designed for a single flight state cannot accomplish the whole transition control of tiltrotors operating in the transition mode.Moreover,the switching LPV control method based on the Lyapunov function is computationally expensive because it needs to solve a large number of linear matrix inequalities.28

The objective of this paper is to propose a control approach which is competent for achieving effective control for tiltrotor aircraft in the transition mode.More specifically,this paper contributes to online model linearization,dynamic generation strategy of reference commands,and real-time optimization based optimal control of a tiltrotor.Firstly,a nonlinear and time-varying Lagrange-form tiltrotor model is presented,which takes the control couplings of tiltrotor aircraft into account.Secondly,how to derive a TVL model from the time-varying nonlinear model is addressed.Note that the TVL model updates its parameters at each sampling instant according to the flight conditions.Thirdly,a trim-condition based approach is developed to calculate the reference commands for airspeed velocity and attitude.To update the reference commands in real-time,a library for the flight envelope of the tiltrotor and the static characteristics curves of the pitch angle is founded.Fourthly,inspired by the MPC concept,an online optimization based optimal control approach is proposed for tiltrotor aircraft,especially when considering transition-mode flight missions.Moreover,the proposed control approach allows for conducting input constraints,and the control inputs are the solution of a constrained online optimization problem.

The structure of this paper is organized as follows.Section 2 presents the longitudinal dynamic model of a tiltrotor which is used for designing a controller.In Section 3,how to calculate the reference commands of the tiltrotor is introduced.The detailed controller design is described in Section 4.In Section 5,three cases of tilting transition missions are simulated and discussed.Finally,conclusions are given in Section 6.

2.Longitudinal nonlinear model of a tiltrotor

A nonlinear modeling method for tiltrotor aircraft was proposed in Ref.5,and the formulation of the nonlinear modeling method is brief l y given in this section for completeness concern.Fig.1 shows the longitudinal diagram of a tiltrotor aircraft.

As depicted in Fig.1,the longitudinal diagram of the tiltrotor aircraft is described in theOgXgYgcoordinate system.TheOgXgYgis an inertial coordinate system which is fixed on the earth ground,and the axisOgYgis parallel to the local plumb line and points upward.The pointOmeans the position of the nacelle shaft while pointAindicates the position of the rotor hub.PointsG1,G2,andGrepresent the mass centers of the aircraft body,the nacelle-rotor system,and the whole aircraft,respectively.Moreover,θ describes the pitch angle,and θNrepresents the nacelle angle,while α indicates the Angle of Attack(AOA).In addition,Vis the airspeed velocity of the tiltrotor.

L,D,andMare the lift,drag,and pitching moments of the aircraft frame(including the aircraft body and the nacelles),respectively,and they are transited from the aerodynamic center to pointG.What’s more,MNmeans the torque to tilt the nacelle-rotor system,andLTrepresents the aerodynamic pull of the rotors,while α1sis the angle between the rotor disc and the hub disc.

According to the Lagrange’s equations,the position coordinates of pointO(x,y),θ,and θNare selected as the generalized coordinates.Let θAF= θ- δAF, θTM= θ+θN-δTM,and θd= θ+θN.Then,the expressions of generalized forces are described as follows:wherem,m1,andm2are the masses of the whole tiltrotor,the aircraft body,and the nacelle-rotor system,respectively,whilel1,l2,andl3denote the lengths ofOA,OG1,andOG2,respectively.

Similar to the case in Ref.4,the nacelles are designed as uniform rotation in this paper.Taking into account that the nacelles should switch between rotating and stopping,the scheduling rules of θNare designed as follows:

whereaandbare both constants,and they equal to –π/90 and –π/30 respectively in this paper.Substituting Eq.(2)into Eq.(1),MNin Eq.(1)can be eliminated.

LetVx=˙xandVy=˙y.Consequently,the longitudinal dynamic model of the tiltrotor aircraft can be described as the following by adding one kinematic equation:

whereqdenotes the pitch angular velocity,and

Fig.1 Longitudinal diagram of a tiltrotor aircraft.

whereI1andI2are the moments of inertia of the aircraft body and the nacelle-rotor system,respectively.

According to the aerodynamic theory of blades,LTand α1scan be calculated as follows:

where Ω, θ0,andB1represent the rotational speed,collective pitch,and longitudinal cyclic pitch of the rotors,respectively.

Aerodynamic coefficients ofL,D,andMwere obtained from wind tunnel test data of Bell Helicopter Company and NASA’s Langley Laboratory.29,30Furthermore,the wings are disturbed by rotor wake in the helicopter and transition modes.1,31As a result,the overall aerodynamic forces and moments without considering the contribution of the rotors can be written into the following form:

wherekandVirepresent the influence coefficient and induced speed of the rotors,respectively,while δemeans the elevator angle.

It is worth noting that there exists a control coupling betweenB1and δe.They are both controlled by the displacement of the longitudinal control bar δlong.

Therefore,four flight states(Vx,Vy,q,θ)and two control inputs(θ0,δlong)used for describing the longitudinal dynamic characteristics of the tiltrotor aircraft are all acquired.Furthermore,let X= ［Vx，Vy，q，θ］Tmean the state variables,and U= ［θ0，δlong］Tmean the control variables.As a result,Eq.(3)can be rewritten into the following general form:

3.Generate reference flight state from nacelle angle

The reference flight state is the desired motion of the tiltrotor in the transition mode.For the tiltrotor transiting from the helicopter mode to the airplane mode,the desired motion is the one that can keep the altitude unchanged and drive the airspeed velocity to increase monotonically during the whole transition process within the safe flight envelope.Note that before determining the reference flight state concerning airspeed velocity commands and attitude commands,the scheduling curve for the nacelle angle is assumed to be chosen according to Eq.(2).

In this section,the reference flight state is generated by analyzing the flight envelope.An off l ine library of the reference commands is founded for real-time visiting during the transition flight.

3.1.Flight envelope and tilting rule determination

The flight envelope shows the safe airspeed velocity ranges of the tiltrotor aircraft at different nacelle angles.Taking the XV-15 tiltrotor aircraft as an example,its flight envelope is shown in Fig.2.Moreover,the horizontal and vertical axes mean the airspeed velocity and nacelle angle,respectively.

Fig.2 Flight envelope and 3 typical transition curves.

There are so many possible tilting transition curves in the flight envelop if the tiltrotor aircraft transits from one certain flight condition in the helicopter mode to one certain flight condition in the airplane mode.For example,Fig.2 demonstrates 3 possible tilting transition curves when the airspeed velocities of the tiltrotor in the helicopter and airplane modes are equal to 30 m/s and 90 m/s,respectively,and their numbers are also annotated in Fig.2.

3.2.Reference for velocity

VelocityVcan be expressed as a function of θNaccording to each tilting transition curve demonstrated in Fig.2.Combining Fig.2 with Eq.(2),the reference ofVcan be defined as follows:

Taking the No.1 tilting transition curve as an example,specific expressions of Eq.(7)are written as follows:

whereV0andVTrepresent the airspeed velocities of the tiltrotor in the helicopter and airplane modes,respectively,whilet0is the time instant when the nacelles are beginning to tilt.Furthermore,Vcan be divided into the horizontal componentVxand the vertical componentVy.In order to keep the altitude,the reference value ofVyshould always be zero.As a result,we have

3.3.References for pitch angle and angular velocity

The reference of θ is generated based on its static characteristics curves in this paper.First of all,we trim the tiltrotor with different nacelle angles for a straight-level flight,and compute static characteristic curves of θ.When the aircraft is in a steady forward flight,θ is equal to the AOA.Moreover,Vx,Vy,and θNare known variables while θ,MN,θ0,and δlongare unknown variables,and the four generalized forces in Eq.(1)are all zero at the equilibrium state.Then these four unknown variables can be derived.As illustrated in Fig.3,there are f i ve static characteristic curves with different nacelle angles.

Fig.3 Static characteristic curves of pitch angle.

As described in Fig.3,one and only one trim pitch angle can be determined by one certain airspeed velocity and one certain nacelle angle.Combining Eqs.(7),(9),and Fig.3,the reference of θ can be expressed as the following equation:

It can be seen that θRefis dependent on θN.Meanwhile,a large amount of computation is required if the static characteristics curves are computed with all nacelle angles,because calculation of the static characteristics curves is complex.Therefore,five trim pitch angles can be obtained according to the five static characteristics curves,and five time instants can be calculated based on Eq.(2).Then an approximate θRefcan be obtained according to the curve fitting results,and it is written as（t）in this paper.Furthermore,the reference ofqcan be expressed as follows:

It should be noted that the beginning of the transition mode is the end of the helicopter mode,and the end of the transition mode is the beginning of the airplane mode.Therefore,the values ofqRef（t）at these two time instants should both be zero,and the highest degree of function（t）should be six because of f i ve known function values and two known derivative values.Consequently,three curves of the approximate reference pitch angles are illustrated in Fig.3.

In summary,the reference flight state can be determined by each tilting transition curve in the flight envelope,and the steps are demonstrated as follows.

Step 1.select a tilting transition curve in the flight envelope.Step 2.calculate VRefaccording to the transition curve and Eq.(2).

Step 3.based on Eqs.(2),(7),and the static characteristics curves of θ,compute θRefand qRef.

Finally,the reference flight state is obtained.

4.Controller design

It is seen from Eq.(6)that,at any instant,the dynamic models of the tiltrotor aircraft can be written as follows:

Moreover,Eq.(13)can be rewritten based on the small disturbance theory as follows32:

where X*and U*represent the basic values of X and U at a certain sampling instant,respectively,while ΔX and ΔU mean the incremental values,respectively.The prerequisite for Taylor expansion is that the system dynamics have continuouslydifferentiable characteristics.In this paper,the tiltrotor flight dynamics have time-varying and continuously-differentiable characteristics in the transition mode;therefore,Eq.(14)can be transited into a linear model using Taylor expansion type real-time linearization as follows:33

Taking （∂f1/∂X1）*as an example,it describes the value of the partial derivative ∂f1/∂X1at a certain sampling instant,and it can be solved as follows:

where δX1is a small quantity.Similarly,the other three equations of Eq.(13)can also be rewritten as the form of Eq.(15).

In advanced control design for nonlinear time-varying systems,a nonlinear model is often linearized at each sampling point while the operating point of the controlled plant is changing.In Trajectory Linearization Control(TLC),Zhu et al.have been using Taylor expansion type real-time linearization and the corresponding linear models to update controller gains.TLC has been applied in the field of space shuttle control(e.g.,application to X33,Marshall space flight center).34Besides,Pu et al.applied TLC to the control of a flexible hypersonic vehicle.35

LetTrepresent the sampling interval,andt=KTmeans the current sampling instant.As a result,we have

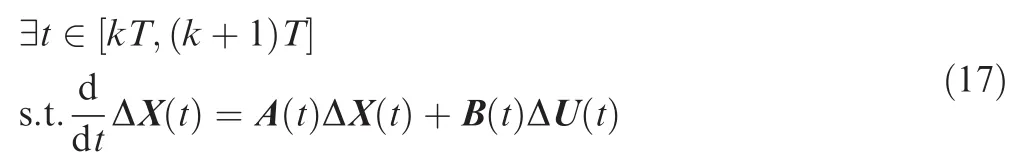
where the order of matrix A is 4×4,the order of matrix B is 4×2,and we have

Obviously,the values of A and B depend on the time,so Eq.(17)is a time-varying linear model.Furthermore,the discrete form of Eq.(17)is

where I4denotes the four-order unit matrix.It is known that

Accordingly,the following formulation can be derived:

This paper defines a function to calculate the basic values of state variables,and the expression of the function is as follows:

In Eq.(21),U*（kT）are the basic control variables at the current sampling instant,X*（t）are the basic state variables after a period of time,and F means that X*（t）is calculated according to the nonlinear dynamic models which are represented as Eq.(3).What’s more,this function lets the initial values of the state and control variables equal to X（kT）and U*（kT）respectively,and then computes new state variables with the control inputs remaining unchanged.Therefore,X*（t）is equal to the new state variables.Obviously,we can get

Consequently,the discrete model can be further written as follows:

where variables with subscript(k)represent their values at the current sampling instant.It can be seen from Eq.(23)that the basic control variables at the current sampling instant are the real control variables at the last sampling instant.The basic state variables at the next sampling instant are calculated according to the real state variables,the basic control variables at the current sampling instant,and the sampling time interval.Moreover,X（k+1）are the state variables at the next sampling instant.As a result,Eq.(23)can be simplified as follows:

Eq.(24)reveals the nature of aircraft dynamics.In detail,the first term on the right indicates the change of the state caused by itself with the control unchanged,and the second term signifies the change of the state caused by a change of the control.

The objective functionJ（k）is used to compute the optimal solution for U（k）and to make X（k+1）close to the references as much as possible,and it also should depress dramatic changes of the control variables as

In addition,the amplitudes and rates of the control inputs are also limited to certain ranges as

where I2means the two-order unit matrix.To minimizeJ（k）subject to inequality constraints,let us consider the so-called Lagrange expression which takes into account the constraints as

where λ（k）contains the Lagrange multipliers.According to the Karush-Kuhn-Tucker condition,the following expression is obtained36,37:

This problem is equivalent to

The minimization over U（k）is unconstrained and attained by

It is known that R is reversible by its definition.Let=Q/β and β≠0.Then it can be proven that H（k）will always be reversible by adjusting the values of Q as follows:

Fig.4 Control diagram of closed-loop tiltrotor aircraft system(the control law part and the controlled plant are located separately in the dashed box).

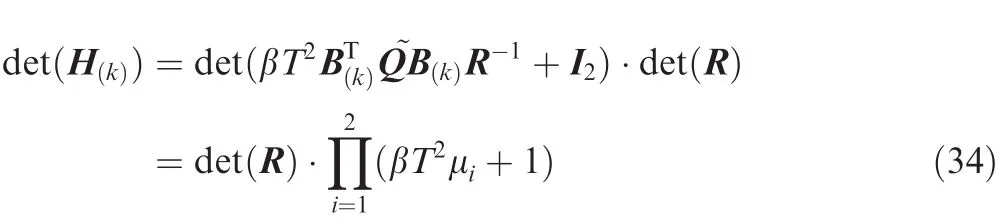
Obviously,there always exists a β which satisfies the inequality that βT2μi≠1（i=1，2）,which ensures that inversion of H（k）exists.Substituting Eq.(32)into Eq.(31),we get

Finally,we use Hildreth’s quadratic programming procedure to minimize the objective function as

subject to λ（k）≥ 0.38Substituting the calculated λ（k）into Eq.(32),the optimal control inputs can be obtained in the following form:

Furthermore,the system structure of the tiltrotor aircraft with the controller is depicted in Fig.4.

5.Simulation results and discussion

To demonstrate the performance of the controller,three scenarios are taken as examples,and the references of the state variables are calculated respectively.These three scenariosare one-by-one related to the three tilting transition curves in Fig.2.It is worth noting that all these simulations are performed using the nonlinear model,and all the results are also obtained from the nonlinear model as described in Section 2.Some inherent parameters of the tiltrotor aircraft are shown in Table 1.Moreover,limitations of the control inputs are presented in Table 2.

Table 1 Inherent parameters of the tilt rotor aircraft.

Table 2 Limitations of control inputs.

The specific expressions of the nacelle angle are described as follows:

As can be seen from Eq.(38),the tiltrotor aircraft flies in the helicopter mode at the beginning,then transfers from the helicopter mode to the transition mode,and finally switches into the airplane mode with nacelle tilting completed.The entire flight process takes 40 s.In addition,there are three vertical gust disturbances during 4–6 s,18–20 s,and 34–36 s of the process.Moreover,the model of the gust is a sine-squared one and its maximum speed is 1 m/s.

As shown in Eq.(25),not only the references of the state variables,but also the values of Q and R are necessary.What’s more,the four parameters of Q are the weights ofVx,Vy,q,and θ,respectively,while the two parameters of R are the weights of θ0and δlong,respectively.This paper selects different weight matrices and compares simulation results,and their values are finally determined as in Table 3.

In addition,an i7-4790 CPU and the MATLAB 2016 software are used to calculate simulation results,and the sampling time interval for the controller is chosen as 100 ms while that for the nonlinear models is chosen as 10 ms.It is noted that the computational cost of solving the optimal control is approximately 2.6 ms.

Table 3 Values of matrix Q and Matrix R.

As a result,simulation results of Scenario 1 are shown in Fig.5.The θN,Vx,Vy,q, θ, θ0, δlong,MN, α represent the nacelle angle,the horizontal velocity,the vertical velocity,the pitch angular velocity,the pitch angle,the collective pitch,the longitudinal control bar displacement,the nacelle tilt torque,and the AOA of the tiltrotor,respectively.Referencesof the horizontal velocity,the vertical velocity,the pitch angular velocity and the pitch angle are calculated according to Eqs.(12)and(38).

In Fig.5,the three parts separated by two dotted lines represent the helicopter mode,the transition mode,and the airplane mode,respectively.As can be seen from these figures,the true states of the tiltrotor can track the reference states well and have good performances in dealing with disturbances caused by vertical gusts.Furthermore,simulation results of Scenario 2 are depicted in Fig.6.Simulation results for Scenario 3 are shown in Fig.7.

It can be seen from Figs.5–7 that the tracking performances forVy,q,and θ are better than that forVx.This is because the rotor pull is mainly used for providing the aircraft lift when the tiltrotor has a large nacelle angle,and it is difficult to provide a sufficient acceleration forVxin the early stage of the transition mode.This is also the reason why the tracking performance forVxshown in Fig.6 is the best of these three simulations.

Fig.5 Simulation results for Scenario 1.

Fig.6 Simulation results for Scenario 2.

As can be seen from Figs.5–7,in the early stage of the transition mode,the tracking performance forVyin Scenario 2 is the best of those in the three scenarios,while the tracking performance forVyin Scenario 3 is the worst.The reason is as follows:the reference airspeed velocity in Scenario 2 increases slowly and smoothly over time in the early stage of the transition mode,but the reference airspeed velocity in Scenario 3 has a sudden change in the early stage of the transition mode.Meanwhile,in the late stage of the transition mode,the tracking performance forVyin Scenario 3 is the best of those in the three scenarios,and the tracking performance forVyin Scenario 2 is the worst.The reason is as follows:the reference airspeed velocity in Scenario 3 increased slowly and smoothly over time in the late stage of the transition mode,but the reference airspeed velocity in Scenario 2 appears a sudden change at the late stage of the transition mode,which can be seen in the first and second subfigures of Fig.7 and Fig.6,respectively.

Considering the impacts of the gust disturbances on a flight,the simulation results show that the tiltrotor is more sensitive to the gust disturbance when the airspeed velocity is higher.The reason is that these disturbances lead to changes of the AoA,and even a small change of the AoA can still cause relatively larger aerodynamic changes when the airspeed velocity is high.

In order to demonstrate the advantage of the controller with input constraints taken into account,this paper takes Scenario 1 as an example to compare the control method which considers the control input constraints to the one which does not consider the constraints.It is worth noting that the controller without considering the control input constraints is derived based on Eq.(25).Responses of θ are illustrated in Fig.8,and the maximum speed of the gust is 14 m/s.Reference command of θ for Fig.8 is the same as that in Fig.5.

As shown in Fig.8,the controller with input constraints taken into account has a better performance than that of the controller which does not consider input constraints.The latter controller results in obvious oscillations in all three flight modes,and the performance for the airplane mode is particularly unsatisfying in the case of gust disturbance.

To summarize,the quadratic programming based optimal controller proposed in this paper is shown to be able to accomplish the tilting transition missions of the tiltrotor aircraft.Except for the transition mode,the controller can also result in satisfying command tracking performance when the tiltrotor operates in the helicopter or airplane mode.Furthermore,the controller can effectively deal with unexpected gust disturbances.

Fig.8 Responses of θ comparison between two controllers.

6.Conclusions

A tiltrotor aircraft is a nonlinear and multibody system with a high degree of freedom,and has strong time-varying characteristics when considering the nacelle tilting procedure.A quadratic programming based optimal control method is developed based on a tiltrotor Time-Varying Linear(TVL)model,and the proposed controller is thoroughly validated in this paper.

(1)The TVL model is derived from a nonlinear Lagrangeform model through online linearization.The TVL model can effectively describe the dynamic characteristics of the tiltrotor in a finite time domain.Based on the TVL model and the regular optimal control strategy,an online optimization based optimal control approach which takes input constraints into account is proposed,and a controller is presented.Moreover,the controller updates the parameters of the TVL model at each sampling instant according to flight conditions.Therefore,the controller can deal with the strong time-varying characteristics and control input constraints of the tiltrotor aircraft.

(2)The proposed control approach is validated using data from an XV-15 tiltrotor.Three typical scenarios are simulated,and abrupt vertical gusts are introduced to show the interference immunity.The results show that the designed controller can achieve desired tracking performance for the tiltrotor throughout its operating envelop which includes a transition flight.In addition,the controller has sufficient capability to handle input constraints and accommodate gust disturbances.

(3)In future research,attention will be paid to how to dynamically generate more reasonable reference commands for airspeed velocity and attitude by considering the tiltrotor maneuverability and energy consumption.

Acknowledgement

This work was supported by the National Natural Science Foundation of China(No.11502008).

1.Carlson EB,Zhao YYJ.Prediction of tiltrotor height-velocity diagrams using optimal control theory.J Aircraft2003;40(5):896–905.

2.Carlson EB,Zhao YJ.Optimal short takeoff of tiltrotor aircraft in one engine failure.J Aircraft2002;39(2):280–9.

3.Sha HW,Chen RL.Flight dynamics characteristic of tilt rotor aircraft.J Aerospace Power2012;27(4):749–54[Chinese].

4.Li HX,Qu XJ,Wang WJ.Multi-body motion modeling and simulation for tilt rotor aircraft.Chin J Aeronaut2010;23(4):415–22.

5.Zhang J,Wu Y,Qu XJ.Flight dynamics modeling of tilt rotor aircraft based on Lagrange equation.Flight Dynam2017;35(3):11–5[Chinese].

6.Banerjee AK.Contributions of multibody dynamics to space lfight:a brief review.J Guid Control Dynam2003;26(3):385–94.

7.Santini P,Gasbarri P.Dynamics of multibody systems in space environment;Lagrangian vs.Eulerian approach.Acta Astronaut2004;54(1):1–24.

8.Li ZQ,Xia PQ.Aeroelastic stability of full-span tiltrotor aircraft model in forward flight.Chin J Aeronaut2017;30(6):1885–94.

9.Mehra RK,Prasanth RK,Gopalaswamy S.XV-15 tiltrotor flight control system design using model predictive control.IEEE arospace conference;1998 Mar 21–28.Piscataway:IEEE Press;1998.

10.Papachristos C,Alexis K,Nikolakopoulos G,Tzes A.Model predictive attitude control of an unmanned Tilt-Rotor aircraft.20thIEEEinternational symposium onindustrial electronics(ISIE);2011 Jun 27–30.Piscataway:IEEE Press;2011.

11.Muro D,Colella MM,Serafini J,Gennaretti M.An optimal control approach for alleviation of tiltrotor gust response.Aeronaut J2012;116(1180):651–66.

12.Oktay T.Performance of minimum energy controllers on tiltrotor aircraft.Aircraft Eng Aerospace Technol2014;86(5):361–74.

13.Pu HZ,Zhen ZY,Gao C.Tiltrotor aircraft attitude control in conversion mode based on optimal preview control.IEEE Chinese guidance,navigation and control conference(CGNCC).Piscataway:IEEE Press;2014.

14.Pan Z,Wang WH,Song SY,Lu K.Nonlinear attitude control aircraft based on active disturbance rejection sliding mode method.IEEE Chinese guidance,navigation and control conference(CGNCC).Piscataway:IEEE Press;2016.

15.Mushfiqul A,Sergej C,Daniel W.Robust hover mode control of a tiltrotor using nonlinear control technique.AIAA guidance,navigation,and control conference.Reston:AIAA;2016.

16.Rysdyk RT,Calise AJ.Adaptive model inversion flight control for tilt-rotor aircraft.J Guid Control Dynam1999;22(3):402–7.

17.Rysdyk R,Calise AJ.Robust nonlinear adaptive flight control for consistent handling qualities.IEEE Trans Control Syst Technol2005;13(6):896–910.

18.Yang X,Fan Y,Zhu J.Transition flight control of two vertical/short takeoff and landing aircraft.J Guid Control Dynam2008;31(2):371–85.

19.Ting S.Finite-time control of linear systems under time-varying sampling.Neurocomputing2015;151(3):1327–31.

20.Li JS.Ensemble control of finite-dimensional time-varying linear systems.IEEE Trans Autom Control2011;56(2):345–57.

21.Vu L,Liberzon D.Supervisory control of uncertain linear timevarying systems.IEEE Trans Autom Control2011;56(1):27–42.

22.Anderson BDO,Ilchmann A,Wirth FR.Stabilizability of linear time-varying systems.Syst Control Lett2013;62(9):747–55.

23.Yue T,Wang L,Ai J.Longitudinal linear parameter varying modeling and simulation of morphing aircraft.J Aircraft2013;50(6):1673–81.

24.Lu B,Wu F,Kim S.Switching LPV control of an F-16 aircraft via controller state reset.IEEE Trans Control Syst Technol2006;14(2):267–77.

25.Lu B,Wu F.Switching LPV control designs using multiple parameter-dependent Lyapunov functions.Automatica2004;40(11):1973–80.

26.Yue T,Wang LX,Ai JQ.Gain self-scheduledH∞control for morphing aircraft in the wing transition process based on an LPV model.Chin J Aeronaut2013;26(4):909–17.

27.Cheng HY,Dong CY,Jiang WL,Wang Q,Hou YZ.Non-fragile switched H-inf i nity control for morphing aircraft with asynchronous switching.Chin J Aeronaut2017;30(3):1127–39.

28.Zhang ZH,Yang LY,Shen GZ.Switching LPV control method in wide flight envelope for hypersonic vehicles.Acta Aeronautica et Astronautica Sinica2012;33(9):1706–16[Chinese].

29.Rosenstein H,McVeigh MA,Mollenkof PA.V/STOL tilt rotor aircraft study mathematical model for a real time simulation of a tilt rotor aircraft.Washington,D.C.:NASA;1973.Report No.:CR114601.

30.Harendra PB,Joglekar MJ,Gaffey TM.Hover low speed and conversion tests of a tilt rotor aeroelastic model.Texas:Bell Helicopter Company;1973.Report No.:301-099-002.

31.Carlson EB,Zhao YY,Chen RTN.Optimal tiltrotor runway operations in one engine inoperative.AIAA guidance,navigation,and control conference.Reston:AIAA;1999.

32.Etkin B.Dynamics of atmospheric flight.New York:Wiley;1972.p.154–65.

33.Pagilla PR,Zhu YL.Adaptive control of mechanical systems with time-varying parameters and disturbances.J Dynam Syst Meas Control-Trans ASME2004;126(3):520–30.

34.Zhu JJ,Banker B,Hall C.X-33 ascent flight control design by trajectory linearization—A singular perturbation approach.AIAA guidance,navigation,and control conference.Reston:AIAA;2000.

35.Pu ZQ,Tan XM,Fan GL,Yi JQ.Uncertainty analysis and robust trajectory linearization control of a flexible air-breathing hypersonic vehicle.Acta Astronautica2014;101:16–32.

36.Brezhneva OA,Tret’yakov AA,Wright SE.A simple and elementaryproof of the Karush-Kuhn-Tucker theorem for inequality-constrained optimization.Optim Lett2009;3(1):7–10.

37.Birbil SI,Frenk JBG,Still GJ.An elementary proof of the Fritz-John and Karush-Kuhn-Tucker conditions in nonlinear programming.Eur J Oper Res2007;180(1):479–84.

38.Chai S,Wang LP,Rogers E.Model predictive control of a permanent magnet synchronous motor.37th annual conference of the IEEE Industrial-Electronics-Society(IECON).Piscataway:IEEE Press;2011.