Lyapunov-based switched-gain impact angle control guidance

Zhongtao CHENG,Lei LIU,Yongji WANG

National Key Laboratory of Science and Technology on Multispectral Information Processing,School of Automation,Huazhong University of Science and Technology,Wuhan 430074,China

1.Introduction

The primary requirement for a guidance law is to reduce relative distance to an acceptable order of magnitude.As time goes on,the task for a missile becomes more diverse and the battlefield becomes more complex in modern warfare.As a result,there arises new requirement for the missile.Many additional constraints,like field of view constraints in Refs.1,2,a desired impact time for salvo attack in Refs.3–5,or a desired impact angle,are imposed to the missile in practical cases.A certain impact angle can maximize the lethality for the missile in a certain mission.Therefore,the guidance law with the ability to achieve certain impact angle has drawn extensive attention.It is of great importance to do research on impact angle control for the missile.

A large number of methods concerning impact angle control guidance are based on the optimal control theory.This category is usually obtained from solution of linear quadratic regulation problem.One typical feature of this category is that the control inputs need to be minimized.An early example of optimal control theory applied to impact angle constrained terminal guidance was in Ref.6on a reentry vehicle,the guidance system could meet the given specifications for a certain region of initial states through adaptive feedback gains.Ref.7found an adaptive proportional-navigation guidance approach to guide a hypersonic lifting vehicle to impact a ground target in a specif i ed direction.In their law,guidelines were provided for the selection of initial condition and control parameters.Ref.8provided the impact angle optimal guidance law in the form of the state feedback.Based on the linear model around the zero-effort collision triangle,Ref.9developed an impact angle control optimal guidance law against maneuvering targets with arbitrary velocity profiles.Ref.10linearized the kinematic equations around a nominal circular trajectory,a new optimal controller based on the inscribed angle rate was obtained.Usually,the guidance command in this category needs the information of time-to-go.

Besides the optimal guidance law,another category is mainly based on classical way like Proportion Navigation(PN)and its variants.Proportion navigation withN＜2 would cause the guidance command to inf i nity as the relative range decreases to 0.While with guidance constant beingN≥2,the PN guidance law could not achieve all angles from-π to 0.Therefore,Ratnoo and Ghose came up with a composite guidance strategy.In their law,an additional phase was added to the PN guidance,in this way,the guidance law could reach any desired impact angle from-π to 0 against stationary targets in Ref.11Then the two-phase PN guidance law was strengthened to work against non-stationary targets in Ref.12Ref.13provided a variant form of PN with a time-varying bias to satisfy the angular constraints.Ref.14presented an indirect way to control the impact angle.An integral bias term was added to the pure PN in order to shape the trajectory of the missile,and the impact angle could be controlled by adjusting the bias term.Ref.15obtained the estimated form of the interception angle from the closed-form linear trajectory solution,and the difference between the desired angle and the interception angle was added to the PN guidance command.Unlike the former mentioned category which solved impact angle optimal control problem by minimum energy constraints,the variants of PN guidance usually need large control effort.

Besides the two categories mentioned above,there were also other forms of impact angle control guidance law.For example,some of these took advantage of the sliding-mode control theory,and some may make use of the geometrical relationship.And there were others based on Lyapunov stability control theory.The first attempt in this direction seemed to be presented in Ref.16After that,some other guidance laws in Refs.17–22with different concerns were obtained from the famous nonlinear theory.The theory was often used to demonstrate global asymptotic stability of the guidance controller.Ref.23presented an integrated method which involved multiple sliding surface control theory.Ref.24considered the speed disadvantage scenario,a generalized variable structure was used to solve the problem,an additional sliding mode surface was added to increase the achievable range.The study in Ref.25addressed a geometric guidance law in the absence of line-of sight rate information.Another guidance law,a new three point guidance law based on the inscribed angle,without the information of line-of-sight angle rate was presented in Ref.26The study in Ref.27involved the time-to-go in the cost function to form a extended optimal guidance law.The study in Ref.28found a way to deal with the look angle constraints and impact angle constraints in the same time.The work presented in Ref.29assumed the guidance command as a polynomial function of time-to-go and the coefficients are determined by terminal constraints.

In this paper,a novel Lyapunov-based Impact Angle Control Guidance(LIACG)is proposed.With the help of the proper control parameter setting,the desired impact angle happens to be achieved in the end.To reach a wider range of impact angle,the guidance law is further developed into a composite one.The first phase is to establish the proper initial condition for the second phase,and the second phase is to f i nish the engagement in a desired impact angle.

The main advantages of the proposed method are highlighted as follows.First,the guidance law is derived from Lyapunov stability theory,which can guarantee the stability of the system.Second,it does not need the estimation of the time-to go,which can simplify the calculation of guidance command and improve accuracy.Third,it does not need a bias term to regulate the error between the instantaneous heading angle and the desired impact angle,which makes the structure of the guidance law simple and feasible.Furthermore,the control effort is much less than that of the energy optimal guidance law.

The paper is organized as follows.In Section 2,a surfaceto-surface engagement geometry is introduced to describe the relationship between missile and stationary target on the ground.Then the engagement problem is formulated and a guidance law is obtained through Lyapunov stability control theory,which ensures the convergence of heading angle error and relative range.In Section 3,a composite strategy is adopted to expand the achievable zones for the missile.In Section 4,algorithm to implement the guidance laws is presented.In Section 5,first,simulations are carried out to demonstrate the advantages of the proposed LIACG;then,different cases are presented to further demonstrate the property of the composite guidance law.

2.Lyapunov-based guidance law design

The main purpose of this paper is to find a guidance law to hit the target in a specif i ed direction.The planar surface-to surface engagement geometry is denoted in Fig.1.The following assumptions are claimed before deriving the kinematic equations.First,the target is assumed stationary.Second,the autopilot lag is so fast that it can be neglected.Third,the missile is flying at a constant speedV.

Here,the heading angle θ is the angle between the velocity vector and the fixed reference axis.The heading error σ is the angle between the velocity vector and the Line of Sight(LOS)vector.The LOS angle is denoted by λ.All angles are positive in the counterclockwise direction.The relationship between these angles is

The two dimensional kinematic equations can be obtained from the engagement geometry as

Fig.1 Engagement geometry.

The instantaneous position of the missile is denoted byxandy,andais the lateral acceleration.The heading angle turning rate is connected with the acceleration by

The range between missile and target is denoted byR.The differential equations governing the range and LOS angle are

The missile head should aim to the target at the instant of attack,which means the heading error should decrease to zero as the engagement processes.Taking this into consideration,the following Lyapunov candidate function is considered in order to reduce the impact angle error as well as the relative range.

DifferentiatingWwith respect to time yields

In order to satisfy the Lyapunov asymptotic stability condition,the following heading error rate is proposed:

in whichcis the control parameter.Substituting Eq.(9)in Eq.(8)results in

Eq.(10)implies that˙Wis negative definite as long asc＞0,and it is obvious thatWis positive definite.Hence,the asymptotic stability condition is satisfied.Dividing Eqs.(9)and(5)side by side yields

Integrating both sides of Eq.(11)yields

Substituting Eq.(12)into Eq.(9),we get

According to Eq.(13),normalized heading error variations with several different control parameters are plotted in Fig.2.Each curve starts from their respective control parameter value.And control value lower than 1 will inevitably cause inf i nity as the relative range goes to zero.

The proposed guidance law can be applied in a midcourse guidance situation as well as the terminal course situation.The relative range of the former situation will not decline to zero,while the latter does.Eq.(13)and Fig.2 demonstrate thatc＜1 will lead to inf i nity as the relative range goes near zero.This valuable information indicates it is necessary to requirec≥1 in the terminal guidance situation.As to the midcourse situation,there is no need to worry about the inf i nity caused by zero relative range,the value of the control parameter just needs to meet the requirement of the Lyapunov stability condition,which isc＞0.So the reasonable range for the control parameter is

Fig.2 Heading error rate variations.

From the above analysis,it is necessary to choose the value ofcas Eq.(14)shows.On one hand,it can meet the requirement of Lyapunov stability theory.On the other hand,it will avoid inf i nity.

2.1.Impact angle variation with c

Combining Eqs.(9)and(6)yields

Integrating both sides of Eq.(15)yields

Substituting Eq.(16)in Eq.(1)yields

Theorem 1.Consider that the missile satisfiesEqs.(13)and(15),the desired impact angle within the achievable area can be obtained through the adjustment of control parameter.

Proof.From the assumed Lyapunov candidate function and Eq.(12),the heading error will vanish as the relative range goes to zero.Then the impact angle is given as

The partial derivative of θfwith respect to control parameterccan be obtained from Eq.(18)as

It is obvious that Eq.(19)is positive,which means the impact angle increases monotonically with increments of control parameter.Corresponding to the monotonous behavior,the minimum angle θfminand maximum angle θfmaxare expressed as

The range of the permissible set［θfmin，θfmax）depends on the initial heading angle and LOS angle.Taking advantage of Eqs.(20)and(21),the desired impact angle demonstrated by Eq.(18)can be expressed in the following way

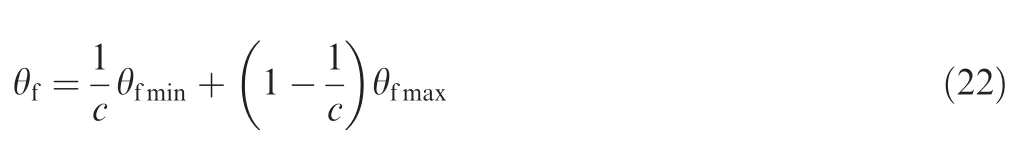
And the actual control parameter connected with the desired impact angle can be obtained from Eq.(22)as

Sincec≥ 1,the set of possible value for θfin the terminal course can be obtained as

As Fig.1 demonstrated,for a surface-to-surface engagement the initial value of LOS angle is

And then the achievable impact angle range is simplified into

The achievable area is shown in Fig.3 in shaded region.If the desired impact angle is in the achievable area,it can be obtained through the adjustment of control parameter.□

Hence,we have proved that the impact angle can be easily adjusted via a single control parameter.With the help of the proper control parameter setting,the desired impact angle happens to be achieved in the end.And heading angle error will converge to zero.

2.2.Acceleration command in the terminal course

Differentiating Eq.(1)with respect to time yields

Substituting Eqs.(9)and(15)into Eq.(27)gives

Fig.3 Achievable area of LIACG in the terminal course.

From Eqs.(4)and(28),the following guidance command can be obtained

Substituting Eq.(12)into Eq.(29)yields

Theorem 2.Consider the guidance law being applied in the terminal course,the magnitude of acceleration demand a decreases as the relative range decreases.

Proof.From Eq.(30)we have Differentiating Eq.(31)with respect toRresults in

Considering Eqs.(14)and(32),the following result can be obtained

Hence,the magnitude of the acceleration in the terminal course decreases monotonically as the relative range decreases.From Eq.(5)we know the relative range decreases monotonically as the engagement proceeds.Then,the maximum magnitude of acceleration demand appears at the initial moment of the engagement and can be expressed as

2.3.Permissible impact angle with acceleration constraint

Assume the maximum acceleration constraint isa*,and we have

Combining Eqs.(34)and(35)we get

in whichc*is the limit value calculated from given maximum acceleration constraint.Combining Eqs.(14)and(36)we get the feasible range forcin the terminal course as

Substitute Eq.(37)into Eq.(18)yields the permissible impact angle with acceleration constraint

3.Composite guidance law

The analysis in Section 2 indicates that the achievable impact angle is seriously relied on the initial conditions.Once the initial conditions are given,the achievable range for impact angle will be set.For a vertical engagement,the impact angle should be able to reach-π/2.If the desired impact angle is in the range as Eq.(38)shows,it can be achieved through the adjustment of control parameter.However,if the desired angle is not in the range for given initial conditions,the only way to achieve the desired angle is to change the initial conditions,which seems unreasonable and impractical.On account of this,it is obliged to set an additional phase to form a composite guidance law.The additional phase is to establish the suitable initial conditions for the latter phase.

3.1.Two phase control strategy

Assume that the first phase also takes advantage of the proposed LIACG law.The first phase is proposed to lead the missile to a suitable initial point for the second phase,and the purpose of the second phase is to hit the target in a desired direction,which means the states at the switching point are the initial conditions of the second phase.Under the proposed strategy,proper switching states are of great importance to achieve a desired impact angle.

In the first phase,the control parameter is denoted byc1,the initial states are λ0and σ0,and the terminal states of this phase are λsand σs,where the subscript s also indicates the switching states.Substituting all these states into Eq.(16)yields

Under the proposed strategy,the terminal states λsand σsin phase 1 are also the initial conditions for phase 2.Control parameter in phase 2 is denoted byc2.Substituting λsand σsinto Eq.(18)yields

Combining Eqs.(39)and(40)yields

Substituting Eq.(40)into Eqs.(20)and(21)yields

Eq.(42)implies the switching states determine the achievable angle set.And λsand σswill not stop changing until phase 1 ends.As a result,the achievable angle set will remain constant once phase 1 ends.The purpose of the composite guidance law is to reach the angles smaller than （λ0- σ0）,which cannot be achieved by single LIACG for given initial conditions.To be capable of achieving this,the value of （λs- σs）must have a decreasing profile with respect to time when phase 1 is taking control.The above analysis indicates that the switching states are affected by the control parameter of phase 1.Furthermore,the switching states and the control parameter in phase 2 determine the impact angle.It is quite necessary to find out the proper relationship betweenc1andc2.

Theorem 3.Concerning Phase 1,the value ofθfminwill decrease monotonously if c1＜c2is satisfied.

Proof.Differentiate Eq.(41)with respect to time,

Using Eqs.(9)and(39)in Eq.(43)results in

if 0＜c1＜c2,then the following equation can be obtained θfmin.

Hence,we have proved that 0＜c1＜c2can guarantee a decreasing profile for the θfmin. □

3.2.Proper control parameters for impact angle-π/2

Former analysis gives the feasible scope for control parameter of both phases.Unlike phase 2,not only the miss distance will not decrease to 0,but also the heading angle has no need to converge in phase 1.Control parameters are proposed asc1=0.0001 in phase 1 andc2=1 in phase 2,respectively.And Theorem 3 verif i es that it is a proper combination to expand the achievable angle range.

The missile follows the trajectory generated by phase 1 until the value computed by Eq.(40)equals to the desired impact angle θd.Then phase 2 takes control,and the desired impact angle can be achieved in the end.The desired impact angle is expressed as

Substitutingc1=0.0001 into Eq.(9)yields

Which means the heading angle error will remain nearly constant in phase 1.As a result,

Consideringc2=1,substitute Eq.(48)into Eq.(46)

Alternatively,the desired impact angle can be achieved by switching fromc1toc2at

The desired impact angle for a vertical strike is θd=-π/2.Replace θdin Eq.(50)with-π/2 to get the switching angle for a vertical strike

Fig.4 Achievable area of two phase LIACG.

Eq.(6)implies that λsdecreases monotonously,which means the suitable switching state for the desired impact angle is unique for given control parameters.As shown in Fig.4,the heading error remains constant before the switching point.Once the impact angle calculated from Eq.(46)equals to the desired impact angle,the control parameter switch fromc1toc2.

And the guidance command can be obtained from Eq.(29)as

a2has been analyzed in Section 2.But the range for control parameter in phase 1 is different.It is obliged to discuss acceleration in phase 1 here.Combining Eqs.(14)and(32)yields

If 0＜c＜1,the magnitude of acceleration demand|a1|will increase as the relative range decreases,and the maximum magnitude of the acceleration will appear at the end of phase 1.Ifc≥1,it will decrease as the relative range decreases,which is the same as the terminal course situation.Then we can get the maximum acceleration in phase 1 as

Rsis the relative range at the end of phase 1,which is also the initial relative range of phase 2.Substitute the switching states into Eq.(34)yields

Considering Theorem 3,it is obvious that

Eq.(56)indicates the maximum magnitude of acceleration in the composite guidance law appears at the switching moment.If the acceleration calculated from Eq.(55)is larger thana*,the guidance law is not suitable for this mission.

4.Implementation

4.1.LIACG

Based on the analysis of Section 2,a desired impact angle in the permissible set can be achieved through a single control parameter.The detailed algorithm is presented in the following steps.

Step 1.Use Eq.(38)to obtain the permissible set Ω.

Step 2.Select an θf∈ Ω.

Step 3.Find the proper c

Step 4.Generate the guidance command.

Step 5.If R＞0.1 m,go back to step 4.If R≤0.1 m,end.

4.2.Composite LIACG

Based on the analysis of Section 3,a vertical strike can be obtained through a proper combination of control parameters and switching time.The detailed algorithm is presented in the following steps.

Step 1.Use Eq.(51)to compute the switching angle λs.

Step 2.Compute the instantaneous λ in each time step.

Step 3.If λ ＞ λs,phase 1 in control.If λ ≤ λs,phase 2 in control.

Step 4.If R＞0.1 m,go back to step 2.If R≤0.1 m,end.

Compared to the existing work,the implementation of proposed guidance law has several advantages.First,the proposed guidance strategy does not need the estimation of the time-togo.This can simplify the calculation of guidance command and improve accuracy.Then,the guidance law does not need a bias term to regulate the impact angle error,which makes the structure of the guidance law simple and feasible.

5.Simulation

For all simulation cases,we consider the missile is flying at a constant speed 270 m/s,and the target is stationary.The initial position for the missile is （x0，y0）=(0 m,0 m),and the target position is （xf，yf）=(8000 m,0 m).The initial LOS angle is zero.The limit value for the acceleration is 8g.All simulation cases are terminated when the relative range is less than 0.1 m.

5.1.Case 1:Comparison between existing work and proposed guidance law

To demonstrate the advantage of the proposed composite guidance law,the Trajectory Shaping Guidance Law(TSGL)in Ref.30and the Optimal Guidance Law(OGL)in Ref.8with impact angle control are considered as comparison.Three major evaluation indexes are final impact angle error,miss distance and control effort,which is calculated by∫|a|dt.The guidance commands for the considered guidance laws are

Initial heading error in this case is σ0=30°.Accordingly,switching angle for the proposed guidance law is computed from Eq.(50)as λs=-60°.The simulation results are presented in Fig.5,solid lines stand for the results of proposed guidance law,missile switches to phase 2 when LOS angle equals to the switching state.Results for TSGL and OGL are demonstrated in dashed lines and dotted lines,respectively.It can be seen from Fig.5 that all the guidance law can lead the missile to the target with a desired impact angle.

The comparison results are in Table 1.Despite the fact that TSGL and OGL were derived by solving the minimum energy problem,the control efforts are larger than that of the proposed LIACG.

In order to hit the target with a desired impact angle,TSGL and OGL would force the velocity vector away from the LOS vector at the beginning of the course.On the other hand,the proposed LIACG applies a guidance command with the same sign of the LOS rate.This keeps the velocity vector close to the LOS angle,resulting in less control effort as well as less flight time.Furthermore,the proposed guidance law does not need the estimation of time-to-go,which makes it quite simple to implement.

5.2.Case 2:Control the impact angle through a single control parameter

The initial heading angle for the missile is θ0=90°for a surface-to-surface engagement.The initial LOS angle and heading error angle can be acquired as λ0=0，σ0= θ0.Using Eq.(22)to get the permissible set of impact angleS= ［-90°，0°）.Consider three typical desired impact angle θd=-90°，-80°and-70°.Control parameter can be calculated by Eq.(23)asc=1，c=1.125，c=1.2857,The simulation results are plotted in Fig.6.

The missile trajectories are presented in Fig.6(a).The corresponding lateral acceleration and impact angle profile are showed in Fig.6(b)and c,respectively.The desired impact angles are achieved successfully with the control parameter obtained from Eq.(23).The heading error is presented in Fig.6(d),where the heading error reduces monotonously all the way to zero as the engagement processes.The behavior proves the effectiveness of the proposed LIACG law.

5.3.Case 3:Composite guidance with different impact angles

Initial states and control parameters are the same for all scenarios in Case 3,but the desired impact angle is different from each other.The very purpose of this case is to show that different switching angles results in different impact angle under the proposed composite control strategy.The switching angles are computed from Eq.(50).The details are demonstrated in Table 2.

Results for Case 3 are shown in Fig.7.The missile trajectories are presented in Fig.7(a).The corresponding lateral acceleration profile is presented in Fig.7(b).There exists a turning point for each missile,but the switch angle is different.The missile with smaller desired impact angle requires more accel-eration.The impact angle profile is plotted in Fig.7(c).The later the switch is,the smaller the impact angle is.Both the impact angle error(see Fig.7(d))and relative range converge to zero in the end.

Table 1 Comparison results.

Fig.5 Comparison of impact angle control methods.

Fig.6 Simulation results under LIACG.

Table 2 Simulation parameters for four missiles with the same initial conditions.

Fig.7 Same initial conditions reach different impact angles under composite guidance law.

5.4.Case 4:Different initial conditions reach the same impact angle

Case 4 is set to demonstrate that different initial conditions can end in a same impact angle as long as the control parameters are calculated through algorithm in Section 4.This property can be put into salvo attack.The detailed control parameters are exhibited in Table 3.

Results for Case 4 are shown in Fig.8.The missile trajectories are presented in Fig.8(a).The missile with lager heading angle error needs more time to achieve the desired impact angle.Corresponding lateral acceleration profile is presented in Fig.8(b).There exists a turning point for each missile,but the switch angle is different due to the different initial conditions.The impact angle profile is plotted in Fig.8(c).Each missile ends in the same impact angle.Both of the impact angle error(see Fig.8(d))and relative range converge to zeroin the end,which shows the effectiveness of the Lyapunov stability control theory.

Table 3 Simulation parameters for three missiles under different initial conditions.

Fig.8 Different initial conditions reach-π/2 under composite guidance law.

6.Conclusions

By introducing Lyapunov stability control theory into impact angle control for the missile,a novel Lyapunov-based guidance law is presented.The impact angle can be adjusted through a single control parameter,while it is affected by initial conditions.Then an additional phase is added to build the ideal initial condition for the second phase,and in turn,the second phase will ensure a desired impact angle.The heading angle error will converge to zero as the engagement progresses,and the impact angle happens to be achieved in the end.This guidance law controls the impact angle in an indirect way.The simulation results verify that the proposed guidance law has many advantages compared to the exiting laws.

Acknowledgements

This study was co-supported in part by the National Natural Science Foundation of China(Nos.61473124,61573161).

1.Wang L,Yao Y,He FH,Liu K.A novel cooperative mid-course guidance scheme for multiple intercepting missiles.Chin J Aeronaut2017;30(3):1140–53.

2.Liang ZX,Li QD,Zhang R.Waypoint constrained guidance for entry vehicles.Aerosp Sci Technol2016;52:52–61.

3.Zhao Y,Sheng YZ,Liu XD.Trajectory reshaping based guidance with impact time and angle constraints.Chin J Aeronaut2016;29(4):984–94.

4.Si YJ,Song SM.Three-dimensional adaptive finite-time guidance law for intercepting maneuvering targets.Chin J Aeronaut2017;30(6):1985–2003.

5.Zhang Y,Ma GX,Liu AL.Guidance law with impact time and impact angle constraints.Chin J Aeronaut2013;26(4):960–6.

6.Kim M,Grider KV.Terminal guidance for impact attitude angle constrained flight trajectories.IEEE Trans Aerosp Electron Syst1973;AES-9(6):852–9.

7.Lu P,Doman DB.Adaptive terminal guidance for hypervelocity impact in specif i ed direction.J Guid Control Dynam2006;29(2):269–78.

8.Ryoo CK,Cho HG,Tahk MJ.Optimal guidance laws with terminal impact angle constraint.J Guid Control Dynam2005;28(4):724–32.

9.Cho HG,Ryoo CK,Tsourdos A,White B.Optimal impact angle control guidance law based on linearization about collision triangle.J Guid Control Dynam2014;37(3):958–64.

10.Tsalik R,Shima T.Optimal guidance around circular trajectories for impact-angle interception.J Guid Control Dynam2016;39(6):1–14.

11.Ratnoo A,Ghose D.Impact angle constrained interception of stationary targets.J Guid Control Dynam2012;31(6):1816–21.

12.Ratnoo A,Ghose D.Impact angle constrained guidance against nonstationary nonmaneuvering targets.J Guid Control Dynam2010;33(1):269–75.

13.Kim BS,Lee JG,Han HS.Biased PNG law for impact with angular constraint.IEEE Trans Aerosp Electron Syst1998;34(1):277–88.

14.Erer KS,Merttopc¸uoglu O.Indirect impact-angle-control against stationary targets using biased pure proportional navigation.J Guid Control Dynam2012;35(2):700–4.

15.Lee CH,Kim TH,Tahk MJ.Interception angle control guidance using proportional navigation with error feedback.J Guid Control Dynam2013;36(36):1556–61.

16.Yanushevsky RT.Concerning Lyapunov-based guidance.J Guid Control Dynam1971;29(2):509–11.

17.Lechevin N,Rabbath CA.Lyapunov-based nonlinear missile guidance.J Guid Control Dynam2004;27(6):1096–102.

18.Kim M,Kim Y.Lyapunov-based pursuit guidance law with impact angle constraint.Proceedings of the 19th IFAC world congress;2014 Aug 24–29;Cape Town.2014.p.2509–14.

19.Saleem A,Ratnoo A.Lyapunov-based guidance law for impact time control and simultaneous arrival.J Guid Control Dynam2015;39(1):1–9.

20.Cho DH,Lee D,Mok SH,Bang H.Lyapunov-based lunar capture guidance scheme.International aerospace congress;2009 Oct 10–12;Daejeon.Seoul:KSAS;2009.p.5290–98.

21.Kim M,Jung B,Han B,Lee S,Kim Y.Lyapunov-based impact time control guidance laws against stationary targets.IEEE Trans Aerosp Electron Syst2015;51(2):1111–22.

22.Yanushevsky R,Boord W.New approach to guidance law design.J Guid Control Dynam2015;28(1):162–6.

23.Chao T,Wang S,Tian G,Yang M.Integrated guidance and control with terminal impact angular constraint for bank to turn flight vehicle.Proceedings of the 33rd Chinese control conference;2014 July 28–30;Nanjing.Beijing:Chinese Association of Automation;2014.p.681–5.

24.Hou ZW,Liu L,Wang YJ,Huang J,Fan HJ.Terminal impact angle constraint guidance with dual sliding surfaces and modelfree target acceleration estimator.IEEE Trans Control Syst Technol2017;25(1):85–100.

25.Ratnoo A,Ghose D.Kill-band-based lateral impact guidance without line-of-sight rate information.J Guid Control Dynam2012;35(6):1740–50.

26.Tsalik R,Shima T.Inscribed angle guidance.J Guid Control Dynam2015;38(1):30–40.

27.Wang H,Lin DF,Cheng ZX,Wang J.Optimal guidance of extended trajectory shaping.Chin J Aeronaut2014;27(5):1259–72.

28.Kim TH,Park BG,Tahk MJ.Bias-shaping method for biased proportional navigation with terminal-angle constraint.J Guid Control Dynam2013;36(6):1810–6.

29.Lee CH,Kim TH,Tahk MJ,Whang IH.Polynomial guidance laws considering terminal impact angle and acceleration constraints.IEEE Trans Aerosp Electron Syst2013;49(1):74–92.

30.Zarchan P.Tacticalandstrategicmissileguidance. 6th ed.Reston:AIAA;2012.p.569–600.