滚珠丝杠副外滚道研磨设备工装优化设计*

温 贵，韩 军，金 俊，欧 屹

(南京理工大学 机械工程学院，南京 210094)

0 引言

滚珠丝杠副是一种精密的功能部件[1]，而研磨是一种重要的精密和超精密加工方法，对于滚珠丝杠副的加工以及失效后的修复，研磨工艺是个十分有必要以及有效的加工方式。合理的研磨加工不仅能满足滚珠丝杠副的精度要求，而且还能改善滚珠丝杠副的性能要求[2]。目前，国内外研磨技术主要有Mori和Tsuwa[3]发明的弹性发射加工装置，Kordonski二十世纪八十年代中期发明的磁流变抛光[4]，今后超精密研磨技术将朝着高精度、高效率的方向发展，这一趋势体现在两个方面：其一是超精密复合加工方法的出现，如化学机械抛光、电解磁力研磨、超声珩磨等，通过多种材料去除机理的协调作用提高加工精度和加工效率；其二是半固着磨粒加工技术的出现，如日本秋田县里大学吴勇波教授提出的磁性抛光体(Magnetic Compound Fluid Polishing Tool)抛光技术[5]。

尽管有这么多的研磨技术，但是运用于滚珠丝杠副加工的研磨技术在国内外发展都并不是很成熟。更重要的是滚珠丝杠副的研磨工艺在国内外都是是一种保密的技术，作为滚珠丝杠副加工的最后一道工序，研磨工艺的技术以及设备是不泄露的。目前，国内外的对滚珠丝杠副的研磨设备主要有喷砂型的研磨设备[6]，这种设备研磨效果比较理想，但是造价一般比较高。本文设计了一种利用与丝杠配合的螺母进行研磨的工装，工装核心是一个具有八瓣对称的柔性研磨螺母，通过聚氨酯弹性体的变形给柔性研磨螺母进行加力，加力方式容易控制，而且能够对柔性研磨螺母施加均匀的周向力，从而使柔性研磨螺母能均匀地研磨丝杠。研磨工装简单有效，能在节省成本的同时，起到理想的研磨效果。

1 研磨工装的设计

环形研磨法这一基础概念已被用于设计新型研磨工具，基于这种理论，本文设计了一种新型精研工具，新型精研工具的显著特征主要有两个部分，即柔性研磨螺母和聚氨酯材料部分。柔性研磨螺母有8个狭缝组成，每边各4个狭缝交替地相隔90°，如图1所示。该研具具有一个平衡机制，即相对于传统的只有两个压力点的研具，它在工件上有更多的接触区域以产生8个方向的均匀研磨压力。

图1 柔性研磨螺母

整个研磨工装的装配图如图2所示。聚氨酯材料部分是两个套在柔性研磨螺母上的厚壁圆筒，这两个部分通过过盈配合使两者之间没有间隙。聚氨酯弹性体外壁以及底面都是通过与外套固定约束的，而聚氨酯缓冲体外壁和上下两个面是不被约束的。聚氨酯弹性体泊松比接近0.5，一旦聚氨酯弹性体变形到与柔性研磨螺母完全抱紧的时候，对聚氨酯弹性体施加的轴向力将会突然变得很大，甚至卡死。聚氨酯缓冲体夹在聚氨酯弹性体和柔性研磨螺母之间，起到了弹簧的缓冲作用，当聚氨酯弹性体受到压力变形后径向变形不会受到完全约束。这样，研磨工装的加力过程就相当于一个非线性的弹簧受力过程，具有可控性。

研磨工装的加力方式是利用螺纹端盖的自锁特性，通过旋转螺纹端盖一定的角度便可对聚氨酯弹性体施加一个稳定的压力。研磨工装在研磨外套靠近螺纹端盖的上边沿设计了一个卡月牙扳手的法兰盘，而螺纹端盖的顶部设计有配合力矩扳手的内六角孔。整个加力过程是通过月牙板手作用到研磨外套以及力矩扳手作用到螺纹端盖的方式进行加力的。通过预先设置好力矩扳手的力矩值，便可以控制螺纹端盖对聚氨酯弹性体下压的压力值。

聚氨酯弹性体与螺纹端盖之间安置了三个LCM300拉压力传感器，当螺纹端盖拧紧时，LCM300受到螺纹端盖稳定的轴向压力，通过LCM300拉压力传感器可以在线监测螺纹端盖对聚氨酯弹性体的轴向压力，当轴向压力达到研磨工艺需要的压力值时，停止拧螺纹端盖即可。

这种新型磨具简单有效，加力方式可控，并且能够提供稳定的研磨压力。研磨丝杠后可以改善轨迹变化，螺旋面误差，甚至提高了滚珠丝杠滚道的表面质量。

1.丝杠 2.柔性研磨螺母 3.研磨外套 4.拉压力传感器支撑架 5.LCM300拉压力传感器 6.压力螺纹端盖 7.拉压力传感器支撑球 8.聚氨酯弹性体 9. 聚氨酯缓冲体 10.外套底座

图2研磨工装装配图

2 研磨工装的建模与分析

研磨工装的建模是为了确定沿着轴向压缩聚氨酯弹性体压力的大小(F)，即可控制的输入量，与柔性研具对滚珠丝杠副外滚道作用的情况，即满足研磨工艺要求的输出量。

当聚氨酯弹性体沿着轴向受到F的压力被压缩时，如图3中的竖直箭头方向，聚氨酯弹性体沿着轴向方向被压缩ΔL，弹性体产生径向的变形，由于弹性体外壁被约束，径向变形只能朝里变形使得柔性研磨齿朝向工件的中心产生在径向方向上的均匀移动，如图3中的水平方向，变形量为Δd，同时，聚氨酯缓冲体径向也被压缩变形Δd，聚氨酯缓冲体受到的径向力F′最终通过内壁压力P作用到柔性研磨螺母上，这将为研磨过程提供稳定的摩擦力。

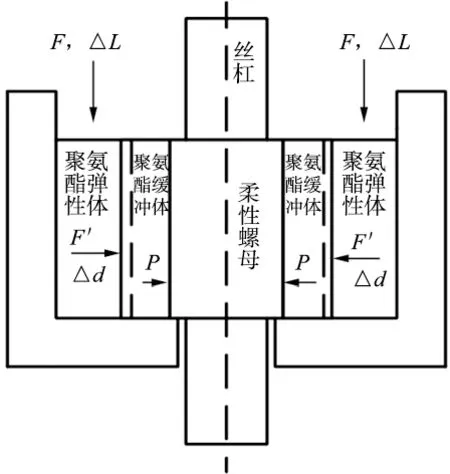
图3 研磨工装受力变形图

2.1 聚氨酯弹性体的本构关系

根据目前超弹性体的研究可知，聚氨酯弹性体的本构模型包括两种：基于应变能密度函数的唯象本构模型以及基于聚合物分子统计学本构模型[7]。

本构模型试验是根据国标GB/T7757-2009进行的，试验材料为聚氨酯，聚氨酯密度为1.2g/cm3，邵尔硬度为60A，试验样件为直径10mm，厚度为2mm的圆柱体，试验中加载的压力为准静态加载，应变速率控制为0.01/s，最终得到应力应变曲线，从而根据应变能密度函数得到聚氨酯弹性体的本构模型。试验得到应力σe(MPa)—应变εe数据，并将应变转换成伸长率，即λ=1+εe。图4所示为Ansys Workbench15.0根据试验得到的数据自动生成的应力—应变曲线。

从图4中曲线可以看出当应变在0.0～0.2之间，应力—应变曲线基本是线性的，表明聚氨酯弹性体在小变形的时候可以看成是线性的变形。当应变大于0.2时，应力—应变曲线成凸型，表明聚氨酯弹性体在应变大于0.2后，如果继续加力压缩，聚氨酯会逐渐的硬化，此时聚氨酯弹性体的变形是非线性的。

图4 应力—应变曲线

最终根据改进的Mooney-Rivlin模型Mooney-Rivlin 5 Parameter形式[9]:

以及试验中得到的应力应变数据可以解得：

μ10=9.285,μ01=-5.7573,μ11=0.7793,μ20=0.6748,μ02=-0.2029所以基于三阶变形张量不变量的聚氨酯弹性体的本构方程是：

由于实际研磨工装中聚氨酯弹性体并不是简单的单轴压缩，所以实际的聚氨酯弹性体的本构方程应该在σe的基础上乘以一个修正系数K，K值应该通过实际工装利用力传感器测出的σz进行确定。

2.2 研磨工装弹性体的弹性力学模型

上节中确定的聚氨酯弹性体的力学关系最终将决定研磨工装中聚氨酯弹性体的弹性模量E。考虑到工装中聚氨酯弹性体的受力情况，可以将该模型看作是弹性力学中厚壁圆筒的力学模型。假设聚氨酯弹性体内径减小Δd，也就是聚氨酯缓冲体的外径减小Δd。

聚氨酯弹性体模型的建立(假设聚氨酯弹性体的外径ρ=Ro内径ρ=Ri)。

该模型的几何方程也叫柯西方程：

该模型的物理方程是：

A和B是待定系数，E为聚氨酯弹性体根据本构模型修正的弹性模量，ν表示聚氨酯的泊松比，ερ表示半径ρ处的应变，εφ表示角度为φ处的应变，σρ表示半径ρ处的应力，σφ表示角度为φ处的应力，σz表示Z轴方向应力。

将柯西方程及物理方程联立并积分得到沿半径方向上的位移方程：

其中D是积分常数。

通过边界条件：当ρ=Ri时μρ=Δd；当ρ=R0时μρ=0可以解得系数A，B，D。

所以当ρ=Ri时，

聚氨酯缓冲体模型的建立(假设聚氨酯缓冲体的外径ρ=R0′，内径ρ=Ri′)。

聚氨酯缓冲体的模型和聚氨酯弹性体模型的本质上是一样的，不同的是边界条件：缓冲体的轴向应力σz=0；R0′=Ri；当半径ρ′=Ri′时，此处的位移μρ′=0；当半径ρ′=R0′时此处的位移μρ′=Δd。可以解得系数A′，B′。

所以当ρ′=R0′时，

当ρ′=Ri′时，

其中，E′为聚氨酯缓冲体根据本构模型修正的弹性模量，v′表示聚氨酯缓冲体的泊松比。

由于σρ=Ri=σρ=R0′，可以解得唯一的Δd，Δd是一个跟σz成正比的值，表示为Δd=Hσz,其中H是一个跟E,v,E′,v′,R0,Ri,R0′,Ri′有关的一个常数。因此聚氨酯缓冲体内壁受到的压力为：

其中，L表示聚氨酯弹性体的厚壁筒的高度，P′表示聚氨酯缓冲体对柔性研磨螺母的表面均匀压力。这个表达式最终表明研磨工装中柔性研磨螺母受到的压力和研磨螺母端盖对聚氨酯弹性体的轴向压力F是成正比的，关系如上式所示。

2.3 柔性研具的有限元分析及优化

通过上节中所求的柔性研磨螺母受到的压力P′，结合Ansys Workbench15.0，设置边界条件进行有限元仿真便可以得到柔性研磨螺母的受力变形情况，最终决定柔性研磨螺母对丝杠研磨压力的作用情况。

基于Kyusojin等人建立的圆形研磨理论[10-11]，可以得到表1，假设研具是正多边形(k边形)，滚珠丝杠副的形状为n边形。表中●表示对应的k值得研具不能把滚珠丝杠副的n值多边消除。

为了使研磨螺母受到均匀的周向压力，k值必须取偶数，其中k=4，k=2时，根据表2，对滚珠丝杠副进行研磨具有较大的局限性，不予考虑。对于k=6和k=8的情况，通过WORKBENCH15.0，分别对这两种情况进行仿真分析，仿真设置如下：材料设置为灰铸铁，由于研具具有较规则的形状，网格划分采用默认尺寸，建立一个柱坐标系，观察沿着柱坐标系x轴方向的变形以及整体的应力分布情况，载荷为圆周方向上均匀的5000Pa(P′)压力。仿真结果如图5所示，图5左上图是k=6时放大65倍的变形情况，图5右上图是k=8时放大65倍的变形情况，图5左下图是k=6时的应力分布情况，图5右下图是k=8时的应力分布情况。

表1 圆形研磨理论

图5 柔性研磨螺母workbench仿真结果

从分析结果的云图中可以得处结论：k=6时，x轴方向最大变形为3.6205×10-4m，最小变形为-3.8978×10-4m，最大应力为2.4499×107Pa；k=8时，x轴方向最大变形为-1.5062×10-5m，最小变形为-2.5697×10-5m，最大应力为2.5419×107Pa。k=6时，沿着x轴方向(柱坐标)的既有正向变形3.6205×10-4m，也有反向变形3.8978×10-4m，而且变形量都比较大，相反，k=8时，变形只有沿着x轴(柱坐标)负方向的变形，最大值为2.5697×10-5m，显然比k=6时小得多，同时最大应力与前者也相差不大，最重要的是k=8时，整个研磨螺母的变形更加均匀，这直接影响研磨螺母施加给滚珠丝杠副的压力是否均匀，这点可以从图5中体现出来，将k=6和k=8两种情况沿x轴(柱坐标)方向的变形放大65倍后的云图，从结果中可以很明显的看得出，k=6时，研磨螺母在受到均匀的周向压力时，它的变形是一个椭圆形，这明显不符合研磨工艺的要求，而k=8时，同样是将沿x轴(柱坐标)的变形放大65倍，研磨螺母基本还是保持圆形。综合分析，研磨工装使用的研磨螺母做成8瓣对称的结构有更好的研磨效果。

基于柔性研具是具有八瓣的对称设计，如图1所示，分析该柔性研具时可以将其视为一个刚柔结合的对象。相邻两瓣研具是通过均匀对称开缝后连接的，在研具受到聚氨酯弹性体对它的较小的均匀压力时，连接处是最容易变形，此时可以将这些连接处都视为柔性结构，而每一瓣的研具可以被视为刚体。当聚氨酯弹性体给予研具的压力越来越大时，连接处变形到一定程度，达到变形极限，连接处将被视为刚体结构，每一瓣的研具将开始进行变形。这正好符合k=8时研磨螺母的变形云图表示的结果，即在每个衔接处具有较大的变形，而远离衔接处具体最小的变形。

3 研磨工装的试验验证

为了验证八瓣研磨螺母对滚珠丝杠副研磨的有效性，必须用研磨工装进行滚珠丝杠副相应的研磨试验。

研磨试验是利用图6所示的摩擦力矩试验台进行的，该测量台检测滚珠丝杠副中丝杆与螺母之间相对运动时，滚动体受到摩擦阻力产生的摩擦力矩，是研究与检测滚珠丝杠副综合性能的重要检测设备。摩擦力矩测量台主要结构包括工作台，工作台上包括支撑尾座、传感器移动测量台、三抓卡盘定位端以及卡盘下面的伺服电机，右边为电控系统控制柜和上面的显示器等硬件。其中力矩测量架通过两条对称安装的滚珠直线导轨副与测量台床身相连，保证力矩测量架轴向运动时受到较小的摩擦阻力。

图6 摩擦力矩试验台

研磨滚珠丝杠的研磨工艺参数如下：研磨速度为30r/min，磨粒为w7，研磨时摩擦力矩为2.5N/m，研磨周次为8个周次(正转8次，反转8次)。研磨完成后，将丝杠置于20℃的恒温室中两小时后，对研磨丝杠进行行程误差，齿形误差，残余应力以及粗糙度的检测。这些参数在研磨前必须先通过样件进行检测，作为原始数据，其中行程误差的检测必须在20℃的恒温室里进行检测。下面将对行程误差，齿形误差，残余应力以及粗糙度这4个参数进行检测分析。

将研磨完的丝杠在相应的检测试验台中进行行程误差，齿形误差，残余应力，表面粗糙度等表面质量指标进行检测，检测结果如表2所示。

表2 表面质量检测结果

从表2得出如下结果：①行程误差从初始的V2π=7.05μm减小到了V2π=3.82μm，V300=12.56μm减小到了V300=5.13μm。从数据表明，研磨工装确实能够改善丝杠的行程误差。②丝杠的左右外滚道的拟合圆半径分别从3.4032mm，3.4097mm变成了3.3743mm，3.3674mm。数据表明研磨能够在一定的程度上改善齿形。③丝杠的残余压应力通过相应的仪器检测后发现，压应力值从-159.1MPa增大到了-488.3MPa。丝杠残余压应力的增大能够极大地提高丝杠的疲劳寿命。④丝杠研磨后粗糙度也有一定的改善，试验数据显示，研磨前的丝杠外滚道粗糙度为0.4185，研磨后减小到了0.2465。检测结果表明此研磨工装对丝杠的研磨是有效的。

4 结论

从一种基于柔性研磨螺母的研磨工装的设计介绍开始，对研磨工装进行理论建模，利用workbench有限元软件对柔性螺母进行分析比较，进行优化设计。同时，利用研磨工装进行了研磨试验，并对研磨前后滚珠丝杠副的行程误差，齿形误差，残余应力以及丝杠外滚道表面粗糙度进行了检测对比。最终，得出了相应的结论：

(1)基于环形研磨理论，以及相应的有限元分析，确定了研磨工装中研磨螺母为等分八瓣的柔性螺母。这种设计的研磨螺母在受到环向的均匀压力时能够保持均匀的变形，比较符合与丝杠配合研磨的实际情况。

(2)通过聚氨酯的单轴拉伸试验得到了聚氨酯弹性体的应力—应变图。利用Mooney-Rivlin模型中的Mooney-Rivlin 5 Parameter形式推出了聚氨酯弹性体的本构关系式，建立了聚氨酯弹性体在研磨工装中的受力数学模型，并且为柔性研磨螺母的受力分析奠定了基础。

(3)根据研磨工装的装配情况，建立了研磨螺纹端盖对聚氨酯弹性体的轴向压力F与聚氨酯缓冲体对柔性研磨螺母外壁压力P′的数学模型关系。

(4)利用研磨工装进行了研磨试验，对丝杠的行程误差，齿形误差，残余应力以及粗糙度进行了检测。检测结果表明此研磨工装对丝杠的研磨是有效的。

[参考文献]

[1] 肖正义. 滚珠丝杠副的发展趋势[J]. 制造技术与机床,2000(4): 11-13.

[2] Tateishi K, Yoshida H. Ball screw and a method for manufacturing the same[P]. US, US9289828, 2016.

[3] 杨建东，田春林. 高速研磨技术[M].北京:国防工业出版社, 2013.

[4] 焦安源, 全洪军, 李宗泽,等. 磁力研磨法光整外环槽的工艺参数研究[J]. 组合机床与自动化加工技术, 2015(10):119-123.

[5] 张文俊，夏亮，段瑞永. 一种浮动研磨装置的设计[J]. 组合机床与自动化加工技术, 2017(2):140-141.

[6] 张红. 高压水射流喷丸机床结构设计探析[J]. 烟台南山学院学报,2015(1): 47-49.

[7] 朱艳峰，刘锋，黄小清，等. 橡胶材料的本构模型[J]. 橡胶工业,2016,53(2): 119-125.

[8] 刘柏峰，李洪璠，丁学用. 基于ABAQUS的聚氨酯弹性体本构关系研究[J]. 电子世界, 2014(13): 57.

[9] Chen S, Li Z. The compressive mechanical properties and constitutive relation of polyurethane elastomer[C]. 2016.

[10] Guevarra D S, Kyusojin A, Isobe H, et al. Development of a new lapping method for high precision ball screw (1 st report)-feasibility study of a prototyped lapping tool for automatic lapping process[J]. Precision Engineering, 2001, 25(1): 63-69.

[11] Guevarra D S, Kyusojin A, Isobe H, et al. Development of a new lapping method for high precision ball screw (2nd report) : Design and experimental study of an automatic lapping machine with in-process torque monitoring system[J]. Precision Engineering, 2012, 26(4): 389-395.

[12] 郭覃. 旋风硬铣削大型螺纹的表面完整性研究[D]. 南京：南京理工大学, 2014.

(编辑李秀敏)