基于在线检测数据的白车身误差控制研究*

董 雪，郭 根，吴卓琦，陈晓波，习俊通

(上海交通大学 机械与动力工程学院，上海 200240)

0 引言

在汽车制造过程中，白车身的制造质量直接关系到整车质量水平[1]，在线检测作为检测白车身制造误差的手段在各大整车厂应用广泛，同时，在线检测数据作为白车身制造质量的体现、制造误差的集合蕴含丰富的制造信息，所以，基于在线检测数据的白车身误差控制的研究基于对白车身生产过程的研究及分析，建立在线检测数据与生产过程的关联模型[2]，实现数据驱动的误差溯源，对于提高白车身制造质量具有重大的意义和作用[3]。

目前常用的处理白车身误差数据的办法有小波分析、EMD(经验模态分解)、贝叶斯网络模型、主成分分析等。上海交通大学王华把小波分析办法用于分析处理车身焊接装配质量检测数据中[4]，美国国家宇航局Huang提出针对车身焊接装配的非平稳信号的特点，EMD(经验模态分解)可将复杂的非平稳信号分解成很多IMF(本征模态信号)的和，之后对各分量进行Hibert-Huang变换，得到瞬时的幅值和频率，以便后续的数据波形项和趋势项的分解[10]。湖南大学的程军圣提出了LCD(局部特征尺度分解办法)，该方法在解决端点效应、降低迭代次数和缩短分解时间上比EMD方法更好[11]。但以上两种方法看似都解决了主观与客观的问题，却免不了其处理数据是一元数据，信息量不足的问题，在车身数据当中，大部分测点的数据特征具有强关联性，这是车身结构的高度相关性决定的，单纯采用一元数据无法揭示多个测量的相互关系，存在很大程度的偏颇。邹景明提出了将动态干预算法融入到多元经验贝叶斯的质量评价中，该法提升了小样本数据量下车声测量数据的质量评价精度，但该方法仍然存在一些问题，比如抽检频率不能太大，且抽检的间隔内发生的任何偏差模式无法检验的问题[12]。在白车身的装焊误差研究中，沈阳理工的崔晶婧[5]，丰云秀[3]等分别提出了因子分析、主成分分析及小波分析的应用。但存在因子分析或主成分分析出的结果只能部分定性却不能定量的缺点。而支持向量机在处理制造过程数据中具有学习能力和泛化能力强，能解决较小样本的制造过程建模的特点，而且结构简单，学习速度快，处理对象即使是高维也对计算复杂度影响很小，且分类面简单的同时又能保证分类精度，对于应用在汽车制造过程具有一定的启发意义。

1 白车身焊装误差的控制方法

一个白车身由大大小小300多个薄板冲压件焊接而成，装夹焊接线上大概会有2000个左右的定位点，整车焊点一般都超过4000个，由于薄板冲压件刚度低，且从冲压到分总成、总成的工序之多，流程之长，在白车身的整个焊装过程会出现大量的误差，再加上白车身冲压件本身的制造误差等，都会积累到最终白车身装焊完毕后确定，所以在汽车制造领域把白车身装焊完成之后测得的所有误差统共称作装焊误差。根据X公司质量部数据统计显示，80%焊装误差的控制主要通过工位上夹具的调整完成。

本文主要研究建立白车身在线数据溯源到“机”的模型，建立在线测量数据与夹具调整量关系模型。

本课题数据来源于X公司某白车身在线测量生产线，主要选择前门、中门匹配区的白车身数据，如图1、图2所示，同时辅以同一时间段夹具调整的情况。课题成员对50天的在线测量状况进行跟踪并记录夹具调整方案。该车型的前门、中门匹配区共有测点16个，同时根据侧围定位的零件尺寸检验表可见，整个侧围外板的控制基准面有25个，而与前门、中门匹配区特征点有关的定位面的夹具有9个，分别是A5，A6，A7，A13，A15，A22，A23，A24，A25。

图1 在线测量的被测点 图2 工装夹具布置

本文以A9位置的夹具为例，建立六个点的测量量与A9夹具调整量的关系。

2 面向夹具调整量预测的改进支持向量机

在上世纪六十年代，Vapnik对统计学习理论开始了钻研，并在1971年最早提出了VC维的理论，为后来支持向量机的提出奠定了最重要及最根本的理论根基；在此根基之上，1982年他提出了结构风险最小化原理，该原理下学习机器存在经验风险和置信风险两大类并统称为机器学习的结构风险，若要提高学习机器的泛化能力就要最大程度的降低结构风险；1992年他和Guyon、Bosers等又提出了最优边界分类器，第二年随即提出非线性最优边界分类器，到1995年他总结之前的发现及理论并提出了SVM分类学习机，将SVM应用于解决模式识别的问题。本文主要利用支持向量机模型建立白车身特征点的在线测量数据与夹具调整量的关系。

2.1 非线性支持向量机模型

支持向量机(support vector machines，SVM)是一种进行二类分类的模型。其根本是定义在特征空间上的间隔最大的线性分类器模型，且最大间隔是它与感知机的区别；除此之外还包括核技巧，这是使它成为实质上的分线性二类分器的原因。

核技巧通过核函数实现，核函数[13]通常定义为：设X是输入空间(欧式空间Rn的子集或离散集合)，又设H为特征空间(希尔伯特空间)，如果存在一个从X到H的映射如式(1)。使得对所有x,zχ，函数K(x,z)满足条件式(2)：

φ(x):χ→H

(1)

K(x,z)=φ(x)·φ(z)

(2)

则称K(x,z)为核函数，φ(x)为映射函数，式中φ(x)·φ(z)为φ(x)和φ(z)的内积。

一般最常用的核函数分四类：线性核函数，多项式核函数，径向基核函数和多层感知机(Sigmoid)核函数。线性核函数如式(3)所示，多项式核函数如式(4)所示，RBF核函数如式(5)所示。Sigmoid核函数如式(6)所示。

K(x,x′)=x·x′

(3)

K(x,xi)=(x·xi+θ)θ，i=1，2，3

(4)

(5)

K(x,xi)=tanh[μ(x·xi)-r]

(6)

针对上述核函数的预测情况，使用某工位上A7夹具X方向的历史调整量和被测特征点25，26，27，28，33，34X方向每次夹具调整时的历史在线测量数据进行建模。历史调整合计100次。特征向量为{Δx25，Δx26，Δx27，Δx28，Δx33，Δx34，X}，并采用五折交叉验证。历史调整量及各特征点的平均偏差如表1所示。

表1 测点数据

如图3所示，当采用线性核函数时，MSE=0.12，极差达到0.64mm。

图3 线性核函数的回归结果

如图4～图6所示，当采用的多项式核函数的最高次分别为2,3,4次时，可以看出MSE和极差都较大。

图4 多项式核函数最高次为2的回归结果

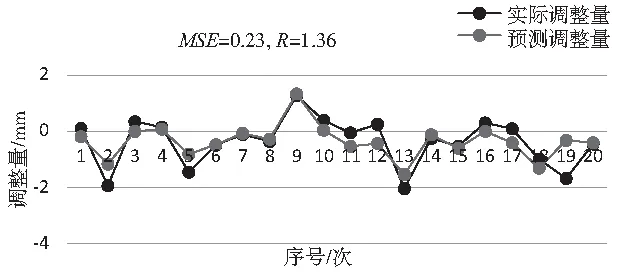
图5 多项式核函数最高次为3的回归结果

图6 多项式核函数最高项为4的回归结果

当采用RBF核函数的支持向量机时，如图7所示，当C=14，g=0.1时，MSE=0.11，R=0.24mm，如图8所示，当C=20，g=10时，MSE=4.25，R=2.3mm，由此可以看出，RBF核函数的预测效果较线性核函数和多项式核函数效果更好，但人工调参具有不确定性。由于核函数的参数直接决定非线性支持向量机的分类能力，核函数参数的优化十分重要。

图7 RBF核函数人工调参回归结果

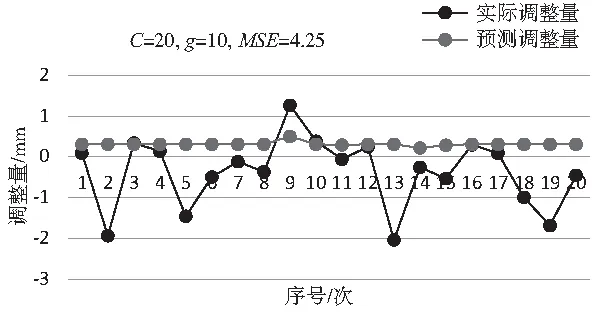
图8 RBF核函数人工调参回归结果

2.2 改进支持向量机算法流程

在RBF核函数中，有两个十分重要的参数：惩罚因子γ和核参数σ，惩罚因子γ决定对处于软间隔内的支持向量的容忍程度，惩罚因子γ越大，容忍程度越高，反之亦然。核参数σ是径向基核函数自带的参数，主要决定映射后产生作用的维数实际大小。常见的参数优化方法有网格搜索法，但网格搜索法速度慢，且其搜索范围受到人工设置的干扰。于是本文引入遗传算法对RBF核函数的支持向量机的参数进行优化，以调高夹具调整量的预测准确率。

和传统的算法比较，遗传算法具有四个不同之处，首先该算法并非直接作用于参变量集，而作用在利用参变量集的某种编码上，其次，该算法使用的是适应值信息，不需要导数或者其他的辅助信息，再者，该算法的起始处不是单点而是一点对应的群体开始搜索。最后，该算法利用的是概率转移规则而不是确定性的规则。同时该算法有两大优越性：①全局优化，即使在其定义的适应函数是不连续非规则及有噪声的情况下，其搜索过程中也不易陷入全局最优或者，并能极大程度上找到整体的最优解。②隐含并行性，由于其并行性的固有特性，十分适合用在大规模的并行计算机上。

使用遗传算法对RBF核函数的支持向量机进行优化的主要思想是：

(1)设定惩罚因子γ和核参数σ的初始值，将每个参数转化为长度为l的二进制编码串并连接起来，其中γ在前，σ在后。确定目标适应度函数，如式(7)。

(7)

(2)设定总群代数M，种群规模为N，则生产一个2l×N的只有0，1的数组P，每一列对应一组惩罚因子γ和核参数σ的取值。设定复制概率pr、杂交概率pε和变异概率pm及终止值等。

(3)利用遗传算法优化支持向量机参数。选取一组惩罚因子γ和核参数σ，代入支持向量机模型中进行学习，并确定适应度函数的值，然后将P中对应的每组二进制串都赋给惩罚因子γ和核参数σ，并计算各适应度值。

(4)选取适应度最小的那组二进制串进行以概率pm变异，或与其他二进制串以概率pε杂交，或者以概率pr对自身的串进行复制，对样本进行学习并计算出各适应度值。续选择步骤(3)中适应度最小的二进制串重复步骤(3)，直至达到适应度函数的终止值，记录下二进制串。

(5)对二进制串进行解码，获得惩罚因子γ和核参数σ的值。

2.3 效果分析

为了评价模型的回归效果，本文引入MSE(平均平方误差)对各模型的回归效果进行度量，便于比较。

网格搜索法的结果如图9所示。

图9 网格搜索法下的RBF核函数回归结果

BP神经网络模型：两层神经网络，输入神经元tansig，输出神经元是purelin。其参数回归情况如图10所示。

图10 算法收敛性

其预测回归结果如图11所示。

图11 神经网络回归结果

当使用改进支持向量机算法建立模型时，该算法的敛散性如图12所示，其回归结果如图13所示。

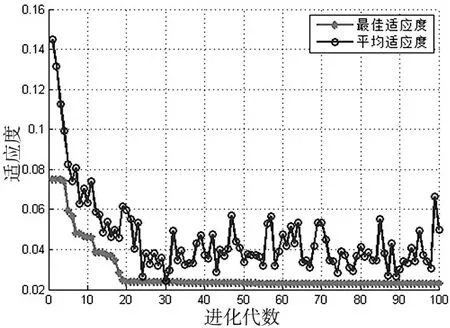
图12 适应度曲线

图13 改进支持向量机回归结果

如表2所示，优化算法的结果和之前采用网格搜索法得到最优参数的模型的结果进行对比，可见改进支持向量机在夹具调整量的回归预测上效果较标准的支持向量机均方差最低，表现出更好的预测准确率和稳定性。

表2 预测结果比较

3 实际应用

某车型白车身的在线测量数据显示在侧围中柱上方出现大面积的偏高。其中测点25，26，27的变化如图14所示，测点28，33，34的变化如图15所示。

图14 测点25,26,27综合偏差的变化情况

图15 测点28,33,34的综合偏差变化情况

(1)经过数据处理显示极差为4.45，标准差为1.23，其中测点34公差范围为±1.00mm,但实际偏差超过公差范围，表现为不合格，且不同测点之间的测点特征表现出强相关性：以测量点28与测量点33为例，相关性达到0.95。超差严重因此需要调整夹具进行控制。根据各工位特点需要对甲工位的夹具A5，A6，A7进行调整，乙工位的夹具A22，A23进行调整。

(2)准备数据，训练模型并根据预测值调整工装夹具，抽取各工装夹具三个方向上的调整量对应的相关点的特征向量，完成训练样本准备。导入改进支持向量机算法模型中进行预测并得到各夹具调整量的值，分别是A5：X0.55mm，Y-0.33mm，Z0.45mm，A6：X-0.89mm，Y0.35mm，Z0.47mm，A7：X0.21mm，Y-0.32mm，Z-0.21mm，A22：X-0.56mm，Y0.35mm，Z-0.47mm，A23：X-0.26mm，Y0.32mm，Z0mm，实际垫片只有0.2mm,0.3mm，0.5mm,1.0mm，2.0mm，所以在调整时要考虑实际情况，A5：X0.50mm，Y-0.30mm，Z0.40mm，A6：X-0.90mm，Y0.30mm，Z0.50mm，A7：X0.20mm，Y-0.30mm，Z-0.20mm，A22：X-0.50mm，Y0.40mm，Z-0.50mm，A23：X-0.20mm，Y0.30mm，Z0mm。

图16 调整前后测点25的偏差

(3)测量白车身生产效果，调整完毕之后，对进入工位后生产成果的白车身的测量点25和测量点34进行追踪，对比调整前后的偏差值状况如图16、图17所示。

图17 调整前后测点34的偏差

通过对比可以看出通过夹具调整之后，测点的偏差有了明显的降低，大部分点都在公差范围之类(±1.00mm)，说明该方法能有效降低白车身的制造误差，具有控制误差的作用。

4 小结

本文使用改进支持向量机模型对工装夹具的调整量进行预测，并在实际生产线中进行应用。通过对比使用预测调整量调整前后的白车身特征点的偏差可以看出：使用改进支持向量机建立夹具调整量预测模型指导工装夹具的调整具有良好的预测效果，能够实现对白车身误差的控制。

[参考文献]

[1] 林忠钦.汽车车身制造质量控制技术[M].北京:机械工业出版社，2005.

[2] 张国辉,党世杰. 遗传算法求解低碳柔性车间生产调度问题[J]. 组合机床与自动化加工技术,2016(11):141-144.

[3] 王灵犀,布占行,刘庆坤. 小波滤波在白车身装焊误差区域识别中的应用[J]. 沈阳理工大学学报,2015,34(4):43-46.

[4] 王华，陈关龙，朱平,等.白车身焊装过程中的小样本采样误差分析[J].机械设计，2003,20(7):48-50.

[5] 丰云秀.主成分分析在白车身焊装误差监控方面的应用研究[D].沈阳:沈阳理工大学，2008.

[6] 张扬明，金隼，陈少云，等.白车身在线检测数据分析方法研究[J].机械制造，2005,43(487):69-71.

[7] D J Cottle. Optimising natural 13 C marker based pasture intake estimates for cattle using a genetic algorithm approach[J]. Livestock Science,2017,197:53-60.

[8] Cortes C, Vapnik V.Support Vector Networks[J].Machine Learning,1995(20):273-297.

[9] Cortes C,Vapnik V.Soft margin classifier[J].Technical memorandum，1997，5640492.

[10] Huang N E,Wu Z A.A Review on Hilbert-Huang Transform:Method and Its Applications to Geophysical Studies[J].Adv Adapt Data Anal.,2009,1:23.

[11] 程军圣,郑近德,杨宇. 一种新的非平稳信号分析方法—局部特征尺度分解法[J]. 振动工程学报,2012,25(2):215-220.

[12] 邹景明.汽车车身检测数据的多元经验贝叶斯建模与质量监控方法[D].上海:上海交通大学,2013.

[13] 朱霄珣,徐搏超,焦宏超,等. 遗传算法对SVR风速预测模型的多参数优化[J]. 电机与控制学报,2017,21(2):70-75.

[14] 秦国华，何志芬，王华敏，等. 基于动力学与遗传算法的工件位置偏离预测与控制方法[J]. 机械工程学报,2017,53(1):110-120.

[15] Kyungro Lee, Hwan You, Jiwon Choi, et al. Development of Pharmacophore-Based Classification Model for Activators of Constitutive Androstane Receptor[J]. Drug Metabolism and Pharmacokinetics,2016.