基于多尺度基本熵和参数优化KELM的电机轴承故障诊断

王冬梅，车一鸣，宋慧欣

(国网冀北电力有限公司技能培训中心，河北 保定 071051)

0 引言

感应电机广泛应用于石油、电力、冶金等工业领域，而滚动轴承又是电机“转子-轴承”系统中的重要组成零部件，其运行状态直接影响电机设备的工作精度、工作效率以及使用寿命。统计数据表明，滚动轴承发生故障的比例约占电机全部故障的40%左右，由此可见，对于滚动轴承状态实施监测与诊断对于保障电机设备安全、平稳运行具有非常重要的实际意义[1-2]。

滚动轴承振动信号具有非线性、非平稳特点，这无疑给其状态准确判别带来阻碍，传统以FFT为基础的方法难以取得较好的分析效果，因此需要不断探寻更为先进有效的状态判定方法[3]。文献[4]使用近似熵(Approximate Entropy，AE)对生理信号进行有效处理，但近似熵对数据长度较为敏感。针对此问题，文献[5]提出了样本熵(Sample Entropy，SE)方法，且被成功应用于机械设备诊断[6-7]。与AE、SE不同，文献[8]提出的排列熵(Permutation Entropy，PE)具有计算效率高、受数据长度影响小等优点，后续Yan等[9]将其成功应用于旋转机械振动信号分析。李锦等[10-11]提出一种基本尺度熵(Base-Scale Entropy，BSE)算法，相比于SE与PE算法，它具有计算简便、快速和抗干扰能力强的优点。对于实际工程信号而言，特征信息不仅蕴含于单一尺度上，其它尺度上也可能含有相应的状态信息，因此利用单一尺度熵值方法来描述信号特征，分析结果存在片面性。为此在文献[12-13]中，作者发挥多尺度化分析方法衡量时间序列不同尺度下复杂性和随机性的优势，分别利用多尺度样本熵(Multiscale Sample Entropy，MSE)和多尺度排列熵(Multiscale Permutation Entropy，MPE)对轴承信号进行分析，均取得了不错的处理结果。受此启发，本文将多尺度基本熵(Mutilsclae Base-scale Entropy，MBSE)算法引入到机械故障诊断领域，用于提取电机轴承振动信号的特征信息。

作为一种新型单隐含层前馈神经网络，极限学习机(Extreme Learning Machine，ELM)[14]在随机确定输入权值和隐层参数的情况下可逼近任意函数，无需迭代即可一次确定网络参数，极大提高了网络训练、学习速率。Huang等[15]通过对比极限学习机与支持向量机的建模求解过程，进一步提出了核极限学习机(Kernel Extreme Learning Machine，KELM)算法。KELM通过非线性映射将线性不可分的模式映射到高维特征空间，从而实现线性可分，有效改善了非核ELM权值随机赋值引起的不稳定问题。并且同传统支持向量机、人工神经网络相比，KELM的泛化能力更强、结构更加简单，在处理模式识别分类问题上优势明显[16]。但由于核函数的存在，KELM算法对参数设置较敏感，为此本文采用人工鱼群算法[17]对KELM的参数进行优化，以降低参数调试工作量，并提高识别准确率。

鉴于电机轴承振动信号非平稳、非线性特点及轴承状态自动判定的现实需求，本文利用MBSE来刻画轴承信号的内在特征，以KELM作为分类器进行状态甄别，提出了基于MBSE和参数优化KELM的电机轴承诊断方法，期望得到良好的分析效果。

1 基本算法简介

1.1 BSE算法

基本尺度熵的计算步骤如下[10-11]：

(1)

(2)

(3)

(4)

(5)根据上述步骤计算出BSE的数值，表达式为：

(5)

1.2 MBSE算法

BSE确定的是时间序列单一尺度的复杂度和无规则程度，MBSE定义为时间序列在不同尺度下的BSE值，反映了时间序列在不同尺度下的复杂度，其计算步骤如下：

(6)

(7)

1.3 KELM算法

ELM是一种单隐层前向神经网络算法，可通过公式表示为[14-15]：

f(x)=h(x)β=Hβ

(8)

其中，x为输入样本，f(x)为网络输出，h(x)和H为隐层特征映射矩阵，β为隐层与输出层的链接权重。

在ELM算法中有：

(9)

其中，T训练样本类别向量矩阵，C为正则化系数。

在隐层特征映射矩阵h(x)未知情况下，可将KELM的核矩阵定义如下：

(10)

则表达式(8)可变换为如下形式：

(11)

使用径向基函数为核函数，即：

(12)

在KELM算法中，需要设定正则化系数C和核函数参数s，且分类结果直接受这两个参数影响。

2 MBSE结合参数优化KELM的诊断流程

本文发挥MBSE算法在信号特征提取上的优势，将其引入到机械故障诊断领域，并与KELM算法相互结合，提出一种基于MBSE和参数优化KELM的电机轴承诊断方法，并且为了降低影响参数C和s的调试工作量，利用人工鱼群算法(Artificial Fish Swarm Algorithm，AFSA)[17]对KELM分类器进行自动优化。同时，为验证基于MBSE特征提取方法在轴承状态分类上的优势，利用基于MSE和MPE的特征提取方法进行对比分析，滚动轴承诊断流程如图1所示，具体步骤如下：

(1)首先设置MSE/MPE/MBSE算法的各项参数，相应参数的选取、设置情况如下：

MSE：MSE中相似容限r一般取0.1～0.25倍原时间序列的标准差(SD)。若r设置过大，则会导致原时间序列重构时丢失信息，反之会造成时间序列对噪声干扰过于敏感，特征提取效果不佳。嵌入维数m设置过大，由于序列长度N与m间需满足条件N=10m-30m，则所需时间序列长度越长，嵌入维数m一般值为2[6-7,12]。文中MSE的参数m取值为2，r分别取0.15SD、0.2SD、0.25SD三种情况。

MPE：MPE中嵌入维数m与时延λ需要设置。若参数m数值设置过大，则所需时间序列长度越长，导致计算量较大，m一般取值为3～7[8-9,13]，文中MPE的参数m取值分别为4和5两种情况。由于时延λ对熵值计算影响较小，文中直接取λ=1。

MBSE：MBSE中嵌入维数m的取值范围一般为3～7[10-11]，且要满足条件4m≤N，N为序列的长度。BSE中常量参数a一般取值为0.1～0.4[10-11]，若a设置过大会导致原始信号划分符号时信息丢失，反之则容易受噪声干扰。文中MBSE的参数m取值为4和5两种情况，a取值为0.2和0.3两种情况。

MSE/MPE/MBSE算法中尺度因子一般取τ≥16。文中时间序列长度统一取N=1024，尺度因子统一取τ=20。

(2)设置好上述参数后，利用MSE/MPE/MBSE算法对轴承10种状态信号样本进行处理，得到不同尺度因子下的样本熵值、排列熵值和基本熵值。

(3)统计MSE/MPE/MBSE的计算总时间和平均时间，分析对比计算效率。

(4)利用步骤(2)中所得各类熵值作为KELM分类器的输入特征向量，并通过AFSA算法搜寻分类器的最佳正则化系数C和核函数参数s。在寻优过程中，将分类精度作为人工鱼群的食物浓度，食物浓度最大化作为最终寻优目标。文中设置鱼群规模N为50、最大移动步长Step为5、感知范围Visual为2.5、迭代次数m为100、拥挤度因子δ为0.6，正则化系数C取值范围为[0，100]，核函数参数s取值范围为(0，600]。

(5)在给定范围内随机生成第一代人工鱼种群，计算初始鱼群中人工鱼个体当前位置食物浓度值FC(即分类精度)，并与鱼群公告板相比较，取最大值写入公告板，将此鱼赋值给公告板。

(6)每条人工鱼模拟追尾行为、聚群行为，选择FC取值较大的行为执行。每条人工鱼行动一次后，比较自身位置FC值与公告板值，若优于公告板，则以自身状态替换。

(7)若迭代计算器未达到设置的鱼群迭代次数m，跳转回步骤(5)。若满足终止条件，则根据所得结果设置KELM分类器的相应参数，随后进行不同测试样本总量下的分类测试。

(8)根据所得结果对电机轴承不同运行状态进行判定，并通过所得分类精度对不同诊断方法的识别效果进行对比分析。

图1 滚动轴承诊断流程

3 实例验证

利用美国Case Western Reserve大学的电机轴承数据对所述方法进行验证。轴承为6205-2RS深沟球轴承，实验使用电火花加工技术在轴承上布置单点故障。电机转速为1797rpm，采样频率为12kHz。所拾取的信号样本分为正常，内圈损伤，外圈损伤，滚动体损伤4种不同故障状态，每种故障状态又依据损伤直径划分为0.1778mm轻度损伤、0.3556mm中度损伤和0.5334mm重度损伤3种不同损伤程度。因此，本文处理的是一个10状态分类问题，实验信号样本总量为500个，10种不同状态信号样本分别为50个，每个样本的数据长度为2048点，信号样本的具体描述如表1所示。根据表1中的滚动轴承振动信号数据得到时域波形如图2所示，由于文章篇幅有限，这里仅以表1中10种不同状态下的一组信号样本为例进行说明。

表1 信号样本的具体描述

通过观察图2可发现，轴承正常状态波形与内、外圈故障波形存在较大差异，但是与滚动体故障波形间的差异则不够明显，此外，同一故障类型情况下不同损伤程度的信号样本也很难准确区别。为此笔者通过熵值算法来提取信号样本的特征信息，并利用KELM分类器来识别电机轴承的不同状态。

首先分别使用MSE/MPE/MBSE算法对信号样本进行处理，分别得到相应20个尺度下的20个熵值特征(即SE1-SE20，PE1-PE20和BSE1-BSE20)，以表1中不同状态下的一组信号样本为例，结果如图3所示。

图2 不同状态轴承信号样本波形

(1) MSE计算结果(r=0.15SD) (2) MSE计算结果(r=0.2SD)

(3) MSE计算结果(r=0.25SD) (4) MPE计算结果(m=4)

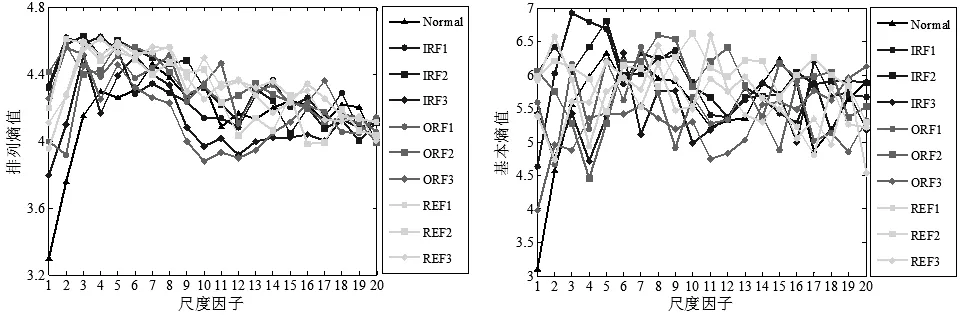
(5) MPE计算结果(m=5) (6) MBSE计算结果(m=4,a=0.2)

(7) MBSE计算结果(m=4,a=0.3) (8) MBSE计算结果(m=5,a=0.2)

(9) MBSE计算结果(m=5,a=0.3)图3 轴承不种状态信号样本的MSE/MPE/MBSE计算结果

下面以表1中滚动轴承每种状态下50个样本进行计算时间统计，总共有500个样本。在此以MSE算法参数r=0.2SD，MPE算法参数m=4，MBSE算法参数m=4、a=0.2为例进行对比，结果如表2所示。

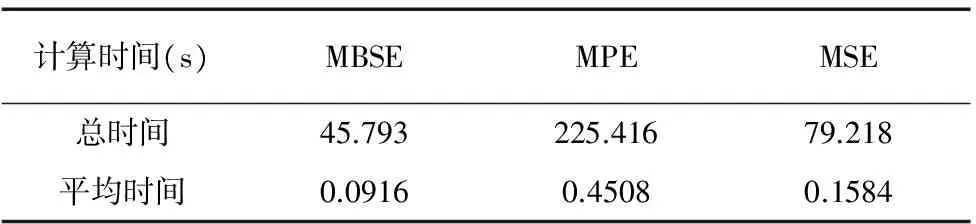
表2 MSE/MPE/MBSE算法计算时间

表2中MBSE算法计算500个信号样本的熵值特征总耗时为45.793s，平均计算时间为0.0916s。MBSE算法的耗时较MSE/MPE算法少的原因分析如下：

(2)BSE算法先利用表达式(2)计算BS数值，这需要进行加、减、乘、除四项基本运算循环操作，相应的循环次数分别为(m-1)(N-m+1)、(m-1)(N-m+1)、(m-1) (N-m+1)和(N-m+1)。

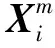
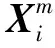
BSE、PE与SE算法所需要的加、减、乘、除、比较、对数运算的次数如表3所示。由于BSE/PE/SE算法中的参数m≥2，故BSE算法的总次数(4m+4m+11)(N-m+1)明显小于PE和SE算法，因此BSE的计算效率高于PE和SE。同时，进行多尺度熵值运算时，需要在每个尺度上分别计算BSE、PE与SE值，因此会加大MBSE/MPE/MSE之间的计算时间落差。

表3 BSE/PE/SE基本运算次数表

表1中信号样本总量为500，分为10种状态类型，且每种轴承状态包含50个样本。分别设置数值为100、200与300的样本量为KELM分类器的训练样本总量，相对应的测试样本总量为400、300、200。其中训练样本总量分为100、200和300的含义为10种不同轴承状态的训练样本分别10、20、30，相对应的测试样本为40、30和20。将SE1-SE20，PE1-PE20和BSE1- BSE20作为KELM分类器的输入特征向量，并使用AFSA算法对分类器进行自动优化，根据第2小节中阐述的操作流程得到MSE/MPE/MBSE三种不同特征提取方法及不同参数设置条件下的27种分类结果，分别如图4和表4所示(由于篇幅有限，只给出部分结果图)，图中蓝色方框标记所示为测试样本实际状态类别，红色星号标记所示为KELM输出的测试样本状态类别。

(1) MSE特征提取法(r=0.15SD) (2) MSE特征提取法(r=0.2SD)

(3) MSE特征提取法(r=0.25SD) (4) MPE特征提取法(m=4)

(5) MPE特征提取法(m=5) (6) MBSE特征提取法(m=4,a=0.2)

(7) MBSE特征提取法(m=4,a=0.3) (8) MBSE特征提取法(m=5,a=0.2)

(9) MBSE特征提取法(m=5,a=0.3)图4 测试样本总量为400时的分类结果

从表4中可以看出，基于MSE特征提取方法的最高分类精度为91.00%(r=0.2SD时)，基于MPE特征提取方法的最高分类精度为95.50%(m=5时)，因此MSE方法分类精度效果最差，MPE次之，而基于MBSE特征提取方法的最高分类精度达到99.33%(m=4，a=0.2时)，较前两种方法的最高分类精度分别提高了8.30%和3.83%。同时基于MBSE/MPE/MSE三种特征提取方法的平均识别精度分别为96.87%，93.50%和85.84%，因此从总体来看，基于MBSE方法的状态分类效果较MPE/MSE方法效果更佳。实验结果表明本文所述诊断方法不仅可以对电机轴承不同的故障类型进行有效判定，而且也可以对同一故障类型下的不同损伤程度进行有效区分。

表4 不同特征提取方法的分类结果

续表

4 结论

本文提出了一种基于MBSE和参数优化KELM的电机轴承诊断方法。首先使用MSEMPEMBSE算法将信号划分到多个尺度上实现特征向量提取。同时，统计、比较、分析了MSEMPEMBSE三种算法的计算效率，相对于MPE/MSE而言，由于MBSE只需计算相邻数据点间的均方数值，不同于MPE/MSE分别需要进行复杂的排序和两次重构等运算，因此计算效率更高。随后利用AFSA算法优化后的KELM分类器对电机轴承的不同故障类型及损伤程度进行识别，最终实验结果表明本文提出的基于MBSE的诊断方法较基于MSE和基于MPE的诊断方法相比能获得更为准确、可靠的状态识别结果，对于实际工程应用来说具有一定指导、借鉴意义。

[参考文献]

[1] CONG F Y, CHEN J. Spectral kurtosis based on AR model for fault diagnosis and condition monitoring of rolling bearing[J]. Journal of Mechanical Science and Technology, 2012, 26(2):301-306.

[2] 丁瑞成,黄友锐,陈珍萍,等. LMD和SVM相结合的电机轴承故障诊断研究[J].组合机床与自动化加工技术, 2016(8):81-84.

[3] 徐卓飞,刘凯,张海燕,等. 基于经验模式分解和主元分析的滚动轴承故障诊断方法研究[J].振动与冲击, 2014, 33(23):133-139.

[4] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences, 1991, 88(6):2297-2301.

[5] RICHMAN J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology Heart & Circulatory Physiology, 2000, 278(6):H2039-H2049.

[6] 赵志宏, 杨绍普. 一种基于样本熵的轴承故障诊断方法[J].振动与冲击, 2012, 31(6):136-140.

[7] ZHU K H, SONG X G, XUE D X. Fault diagnosis of rolling bearings based on IMF envelope sample entropy and support vector machine[J].Journal of Information & Computational Science, 2013, 10(16):5189-5198.

[8] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17)174102.

[9] Yan R Q, Liu Y B, Gao R X. Permutation entropy: a nonlinear statistical measure for status characterization of rotary machines[J]. Mechanical Systems and Signal Processing, 2012, 29(5):474-484.

[10] LI J, NING X B. Dynamical complexity detection in short-term physiological series using base-scale entropy[J]. Physical Review E, 2006, 73(1):88-101.

[11] 李锦,宁新宝.短时高频心电图的基本尺度熵分析[J].中国生物医学工程学报, 2007, 26(4):508-512.

[12] ZHANG L, XIONG G L, LIU H S, et al. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference[J]. Expert Systems with Applications, 2010, 37(8):6077-6085.

[13] TIWARI R, GUPTA V K, KANKAR P K. Bearing fault diagnosis based on multi-scale permutation entropy and adaptive neuro-fuzzy classifier[J]. Journal of Vibration and Control, 2013, 21(3):461-467.

[14] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1-3):489-501.

[15] HUANG G B, ZHOU H M, DING X J, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man and Cybernetics, Part B: Cybernetics, 2012,42(2):513-529．

[16] 马超,张英堂,李志宁,等.基于核极限学习机的液压泵特征参数在线预测[J].计算机仿真,2014,31(5):351-397.

[17] 朱维娜,林敏.基于随机共振和人工鱼群算法的微弱信号智能检测系统[J].仪器仪表学报, 2013, 34(11): 2464-2470.

(编辑李秀敏)