基于流形学习与学习矢量量化神经网络的齿轮故障诊断模型*

魏永合，刘 炜，杨艳君，王志伟

(沈阳理工大学 a.机械工程学院；b.信息科学与工程学院，沈阳 110159)

0 引言

在机械工业领域中，齿轮是广泛应用于各类机械的传动部件之一，而齿轮振动信号与齿轮工作状态密切相关。考虑齿轮在传动过程中均存在振动噪声干扰巨大、信号特征非平稳和非线性、早期故障征兆不明显以及各种典型故障信息之间互相耦合以及高维的数据样本等特点[1]，传统的仅仅基于信号处理的方法通过采用时频域或时频分析等现代信号处理方法直接对采集的齿轮故障信号进行处理以及另一种从微观角度研究故障的起因及其发展规律，通过系统结构和工作原理分析齿轮的损伤或劣化过程的方法已经都不能做到及时准确地对齿轮故障进行诊断甚至预测。而现在常见的主成分分析以及线性判别分析等线性方法在特征提取时又难以直接处理高维数、非结构化的非线性数据[2]；而基于循环迭代求解最优解的自组织映射神经网络在特征提取处理数据时也存在模式识别计算复杂、变量和学习过程不稳定的问题以及BP神经网络算法处理数据时也会易陷入局部最优解的风险[3]。

研究齿轮故障诊断问题的核心是模式识别的方法，而其中故障特征的选择和提取又是齿轮故障诊断的基础[4]。如何选择和提取最有效的故障特征直接影响着齿轮故障诊断的精度。为了对齿轮的故障进行更加全面的描述，通常从时域、频域等多方面选择提取大量的高维故障特征来进行故障诊断[5]。随着现代数字信号处理方法的不断发展，一些新的高维非线性分布数据的特征提取方法相继被提了出来。流形学习作为一类能有效发掘“高维”数据中潜在的非线性结构及其几何特征的有效方法，具有良好的提取齿轮故障数据内在的“非线性”结构信息的能力并且近年来一些改进算法还能有效地抑制噪声的干扰[6]。尹焕[7]利用流形学习理论改进之后的ISOMAP算法对机械故障信号数据集进行非线性降维处理，使得故障数据更加易于分类，为流形学习ISOMAP算法应用于齿轮故障诊断模型实现非线性故障特征压缩提取奠定了一定的理论与实践基础。而LVQ神经网络则广泛应用于各类故障模式识别和优化领域。杨克强[8]通过比较分别采用BP神经网络和LVQ神经网络对齿轮箱的机械故障已有的特征集进行模式识别的结果，提出LVQ神经网络在机械设备故障诊断的应用中更具优势。

针对齿轮非平稳、非线性故障振动信号及其高维数据样本的特点以及流形学习ISOMAP算法对样本噪声很敏感的问题[6]，现已出现了许多关于非平稳振动信号的预处理方法。而本文则结合采用小波去噪的改进的集合经验模态分解算法[9]对非平稳、非线性的齿轮故障振动信号进行预处理的基础上，以降低传统的直接利用流形学习算法时噪声对其低维流形结构的严重干扰。然后再采用流形学习方法对降噪预处理的非线性故障数据进行维数约简，并对ISOMAP算法降维压缩提取的齿轮故障高维非线性多域特征集内在的低维流形结构数据特征再结合采用更加高效的LVQ对其进行模式识别进一步提高了故障诊断的精度，并且降低数据维数将花费更少的时间来训练神经网络模型。最后通过比较实验结果来验证该模型的可行性。

1 流形学习方法基本原理和学习矢量量化神经网络算法

1.1 流形学习方法基本原理

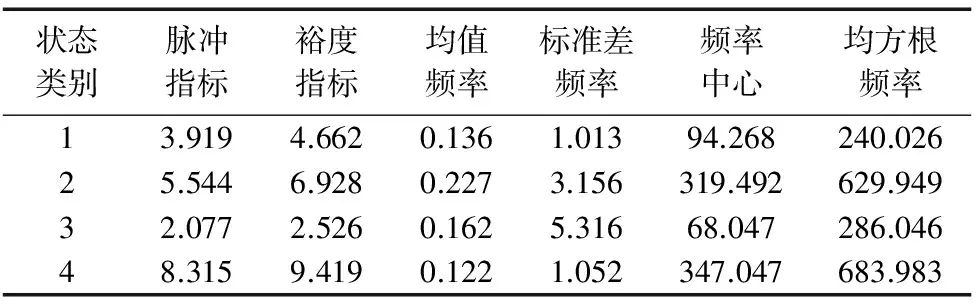
流形学习方法可以实现从高维观测数据中探测出样本点在低维流形空间的嵌入映射结果。给定一个高维数据集D={x1,x2,…,xl}∈RN,假设它处于由坐标图h:M→Rd所确定的内在d维(d

ISOMAP是利用测地距离代替欧氏距离来改进经典多维尺度算法的一种方法，其主要步骤如下[2]：

(1)基于每个数据点对xi和xj之间的欧氏距离dD(i,j)(i,j=1,2,…,l)，确定哪些点是近邻的并构建加权图G,权重为dD(i,j)；

(2)在图G上计算xi和xj之间的最短距离dG(i,j),得到图距离矩阵DG=(dG(i,j))l×l；

(3)将矩阵DG作为经典多维尺度算法的输入得到一个d维嵌套。

1.2 学习矢量量化神经网络算法

学习矢量量化神经网络(Learning Vector Quantization，LVQ)是一种用于训练竞争层的有监督学习方法的输入前向神经网络。它的自适应、自学习以及对非线性系统的分析能力可以有效地根据样本的特征将样本划分到一定的类别中去。它由输入层、竞争层和线性输出层3层神经元组成，输入层与竞争层采用全连接的方式，竞争层与线性输出层采用部分连接的方式。而线性层则会将竞争层传递过来的分类信息转换为使用者所定义的期望类别。

LVQ神经网络算法的计算步骤如下[8]：

(1)网络初始化。用较小的随机数设定输入层和竞争层之间的初始权值。

(1)

式中，wij为输入层的神经元j与竞争层的神经元i之间的权值。

(3)选择与权值向量距离最小的竞争层神经元，若di最小，则与之连接的线性输出层神经元的类标签为Ci。

(4)更新连接权值。记输入向量对应的类标签为Cx，如果Ci=Cx，称为正确分类，则用公式(2)调整权值：

wij_new=wij_old+η(x-wij_old)

(2)

如果没有正确分类，则用公式(3)调整权值：

wij_new=wij_old-η(x-wij_old)

(3)

(5)判断是否满足预先设定的最大迭代次数，满足时算法结束，否则返回步骤(2)进行下一轮神经网络学习。

2 建立基于ISOMAP和LVQ的齿轮故障诊断模型

本文提出的基于流形学习与LVQ的齿轮故障诊断模型，其模型如图1所示，主要包含以下几个步骤：

图1 基于流形学习与LVQ的齿轮故障诊断模型

(1)当齿轮发生故障时，由于其本身及周围系统环境等振动噪声的干扰，其故障信号往往呈现出非线性、非平稳的特征，且包含的频率成分通常都比较复杂。该模型先将原始振动信号通过结合小波去噪的改进的EEMD预处理分解为一系列的IMF分量，这些分量包含了从高到低的频带。通过采用皮尔逊相关系数法可得到各个IMF分量与原始振动信号的相关系数[9]。相关系数越大的IMF分量，包含原始振动信号的特征信息量就越多。选取其中与原始振动信号相关性较好的前l阶IMF分量进行故障特征提取。

(2)将每阶IMF分量经过传统时频域的信号处理方法，提取m个时域特征，其中包括i个有量纲时域特征参数和j个无量纲时域特征参数以及另外n个频域特征参数，总共可以提取m+n个混合域特征[10]，即高维观测样本空间的样本维数为m+n。

(3)将高维观测样本中的特征参数作为ISOMAP算法的输入进行维数约简，分别取嵌入维数d为1、2、3、4进行ISOMAP算法流形学习来寻找结果表达最为直观的嵌入维数，同时分别取近邻数k为8、9、10、15、20、25、30、35对高维齿轮故障观测样本数据进行ISOMAP算法流形学习来寻找特征分离效果比较理想的最佳近邻数，完成对高维样本数据进行的非线性特征提取，提取出用于齿轮分类识别的低维特征样本，构成低维特征样本空间。

(4)训练设定神经网络的相关参数，随机选取x个低维特征样本对LVQ神经网络进行训练，并利用训练好的LVQ神经网络再对随机选取的y个低维特征测试样本进行模式识别。

3 实验验证及实验结果分析

3.1 齿轮原始信号获取

本文采用齿轮故障诊断模拟实验来验证该故障诊断模型的可行性，并模拟齿轮正常状态和齿轮齿根断齿及齿轮齿面点蚀两种常见的故障，分别用加速度传感器采集多组齿轮各种状态下的工作振动信号。

齿轮箱输入轴小齿轮齿数为z1=55，输出轴大齿轮齿数为z2=75，齿轮的模数m=2，齿轮箱为浸油式润滑。电机转速为1500 r/min，采样频率为5120Hz，采样点数为8192。加速度传感器布置在齿轮箱输出轴的端盖X、Y方向上来采集振动信号。图2为齿面点蚀状态下故障振动信号。

(a)齿面点蚀状态下故障振动信号时域波形

(b)齿面点蚀状态下故障振动信号EEMD分解结果图2 齿面点蚀状态下故障振动信号

3.2 特征选择与特征提取

首先为消除指标之间的量纲影响，提高故障识别的准确性，需要对采集的振动数据进行归一化处理，即将数据映射到0～1之间标准化处理使各指标处于同一数量级，解决数据指标间的量纲差异性和可比性问题。通过结合小波技术对小波系数作软阈值处理去噪的改进的EEMD[9]将采集的原始振动信号分解为一系列的IMF分量，由于EEMD是在EMD的基础上进行改进的算法，它是根据EEMD的分解过程中的信号和加入的白噪声的特点来选择EEMD的参数，算法执行EMD的总次数为100,信号中加入白噪声的幅值标准差比值系数为0.1。如图2b为齿面点蚀状态下故障振动信号EEMD分解结果。

根据皮尔逊相关系数法结果，如图3所示，相关系数小于0.2的IMF视为伪分量予以剔除。选用齿轮的第3～6阶IMF分量进行故障特征提取，对信号进行EEMD分解后的分量进行重构并选择特征，在能保留信号主要信息的条件下有效抑制噪声的影响。将每阶IMF分量经过传统时频域的信号处理方法，提取8个时域特征，其中包括均值、均方根值、偏斜度、峭度等4个有量纲时域特征参数和波形指标、峰值指标、裕度指标、脉冲指标等4个无量纲时域特征参数以及均值频率、频率中心、均方根频率、标准差频率等4个频域特征参数，这样，每个样本空间都由这12个特征参数构成，来构造12维的高维观测样本空间。部分测试数据如表1和表2所示。

图3 IMF分量的相关系数曲线

由12个特征参数构成的高维故障样本空间难以直接得到满意的故障诊断效果，并且高维故障特征间存在的大量冗余信息也会削弱故障特征的可辨识性。

表1 齿面点蚀故障的流形学习样本特征向量

表2 齿面点蚀故障的流形学习样本特征向量

为经EEMD预处理的d=3、k=35时提取的样本特征，如图4所示。

图4 未经EEMD预处理的d=3、k=35时提取的样本特征

首先将高维故障观测样本矩阵输入ISOMAP算法，取d=3时在保证含有大部分故障样本信息的前提下对上述齿轮三种特征量具有最佳识别效果，且选取第一个、第二个以及第三个最重要维度为坐标时结果可视化表达也最为直观。同时通过比较结果，发现k=35为最佳近邻数，从图中可以看出，齿轮正常状态、齿轮齿面点蚀以及齿轮齿根断齿都能非常好地区分出来，而且不同类特征聚集度非常高。其故障特征提取结果如图5所示。

图5 EEMD预处理后d=3、k=35时提取的样本特征

从图5可以看出齿轮3种不同的特征量被投影在不同的区域，并且相同的特征量呈现比较集中出现在一个区域并表现出具有一定的分布规律的现象[11]。一般来说，如果在数据映射的过程中不能很好地抑制或者消除噪声的影响，则在低维空间就不能很好地保持原始高维数据之间的拓扑结构信息。对比图4、图5结果可以看出，相比没有去噪等预处理的ISOMAP算法流形学习结果，由于噪声的影响，高维数据在低维空间的流形结构出现了不同程度的扭曲、混叠和变形，一方面低维流形拓扑结构没有完全展开并出现不规则的形状，另一方面局部的各种颜色的样本点仍混杂压缩在一起；而采用EEMD进行预处理后再采用ISOMAP算法提取的齿轮的3种特征量之间几乎没有太大混叠现象出现，特征提取效果比较理想，也有利于下一步故障诊断分类的进行。

3.3 模式识别

将LVQ神经网络竞争层神经元个数设定为20，用于对输入向量进行分类。每类齿轮特征各随机选取30个样本。为不失一般性，随机再从中选取60组数据作为训练样本，剩余30组数据作为测试样本。由于流形学习ISOMAP算法的嵌入维数d=3，故网络的输入层包含3个神经元。输出状态设置为：齿轮正常状态、齿轮齿根断齿、齿轮齿面点蚀，即输出状态类别数为3。将3种齿轮故障特征进行状态编码，其中：1表示齿轮正常状态；2表示齿轮齿根断齿；3表示齿轮齿面点蚀。图6为LVQ神经网络测试的效果。

图6 LVQ神经网络测试的效果

3.4 实验结果比较

BP(Back Propagation Neural Network)神经网络[12]是目前故障诊断领域应用最广泛的神经网络模型之一。为了便于比较，本文利用BP神经网络和LVQ神经网络算法分别对流形学习ISOMAP算法提取的齿轮故障特征进行诊断，通过建立LVQ神经网络和BP神经网络故障诊断模型，然后分别对样本进行训练和测试。对经过训练后两种模型的测试效果如图6、图7所示。

图7 BP神经网络测试的效果

表3 两种神经网络的诊断准确率对比

由表3可以看出，通过LVQ神经网络对流形学习ISOMAP算法提取的故障特征进行诊断，其诊断正确率为29/30=96.7%。而通过BP神经网络对流形学习ISOMAP算法提取的故障特征进行诊断，其诊断正确率为27/30=90.0%。相比较而言，LVQ神经网络模型的故障诊断方法更具精确性。另外，由于流形学习对齿轮特征属性进行了有效约简，也使得基于流形学习与LVQ的故障诊断模型的执行效率得到较大的提高。

4 结论

本文提出一种基于流形学习与LVQ的齿轮故障诊断模型，根据实验结果可以得出以下结论：①由于噪声等因素对流形学习ISOMAP算法的干扰以及齿轮各高维特征间存在的大量冗余信息也会削弱特征的可辨识性，而采用EEMD+ISOMAP算法对原始高维故障特征进行特征提取可以有效提高特征分类的准确率；②齿轮故障模拟实验的结果验证了该模型的有效性，由实验结果可以看出基于LVQ神经网络模型的诊断正确率高于广泛应用于故障诊断领域的BP神经网络模型。

[参考文献]

[1] 宋涛，汤宝平，李锋.基于流形学习和K-最近邻分类器的旋转机械故障诊断方法[J].振动与冲击，2013，32(5):149-153.

[2] 王冠伟，张春霞，庄健，等.流形学习在机械故障诊断中的应用研究[J].工程数学学报，2012，29(4):593-598.

[3] 龙泉，刘永前，杨勇平.基于粒子群优化BP神经网络的风电机组齿轮箱故障诊断方法[J].太阳能学报，2012，33(1):120-124.

[4] 蒋全胜，李华荣，黄鹏.一种基于非线性流形学习的故障特征提取模型[J].振动与冲击，2012,31(23):132-136.

[5] 苏祖强，汤宝平，赵明航，等.基于多故障流形的旋转机械故障诊断[J].振动工程学报，2015，28(2):309-315.

[6] 李波．高维数据的流形学习分析方法[M]．武汉:武汉大学出版社，2016.

[7] 尹焕.基于ISOMAP的机械故障诊断方法研究与应用[D].广州:华南理工大学，2012.

[8] 杨克强.LVQ神经网络在齿轮箱故障诊断中的研究[D].合肥:安徽农业大学，2010.

[9] 魏永合，王明华，林梦菊，等.基于改进EEMD的滚动轴承故障特征提取技术[J].组合机床与自动化加工技术，2015(1):87-90.

[10] Lei Y G，He Z J，Zi Y Y.A new approach to intelligent fault diagnosis of rotating machinery[J].Expert Systems with Application，2008,35(4):1593-1600.

[11] 王广斌.基于流形学习的旋转机械故障诊断方法研究[D].长沙:中南大学，2010.

[12] 于婷婷.基于BP神经网络的滚动轴承故障诊断方法[D].大连:大连理工大学，2008.