基于LabVIEW和PXI的电动直线加载系统

徐志伟，范元勋

(南京理工大学 机械工程学院，南京 210094)

0 引言

快速响应的燃气阀门控制机构是保证固体姿轨控发动机控制的关键，对于提高导弹和火箭运行中调姿、变轨的精准性和机动性，有着重要意义[1]。而传统电磁阀因电磁滞后等原因逐步被一种新型电动伺服阀所取代。

ELLS为被动式负载模拟系统，电动伺服阀在受载条件下所作的主动位移输出会干扰ELLS的加载力输出，进而降低ELLS控制精度，故多余力的抑制方法是ELLS设计中的关键难点[2]。文献[3]应用一种改进型CMAC复合控制方法，通过新的权值更新方法来提高输出平滑性；文献[4]提出一种把幅相辨识和遗传算法结合起来的矢量匹配法，可使误差控制在1%以内；文献[5]采用了引入位置前馈的三闭环控制方法，并应用P型控制器修正信号相位、幅值，有效提高了加载精度；文献[6]采用摆杆来进行直线加载，但达不到自动加载的要求。在国内外研究中，电动加载系统多余力/力矩的抑制多倾向于扭矩式加载，直线式加载若采用滚珠丝杠等运动转换，则其机械结构复杂，摩擦、机械谐振及连接间隙等原因影响着系统加载精度；直线电机控制难度大，成本昂贵，且被测对象直线输出所导致的多余力更难抑制。

为测试此电动伺服阀性能，且由于PXI总线数据传输能力强、兼容性好[7]，基于PXI总线和LabVIEW，设计了一种电动直线加载系统(Electric Linear Loading System, ELLS)。在结构上，采用永磁同步电机(PMSM)作为ELLS的驱动执行元件，采用大导程无自锁精密滚珠丝杠副作为中间传动元件；采用先进的PXI总线搭建了ELLS的硬件架构，选用LabVlEW开发了上位机软件平台；提出一种基于电流内环、位置内环和力外环的三闭环复合控制方法，并在电流内环中采用基于复矢量PI控制的电流耦合补偿方法。对ELLS进行了信号跟踪实验，结果表明ELLS以较高精度有效地测试了电动伺服阀，所提控制方法较好地抑制了多余力。

1 ELLS结构与工作原理

1.1 ELLS结构

ELLS由控制台、试验台及配电柜三部分组成，三部分的组成、连接关系如图1所示。试验台由PMSM加载系统、运动转换系统、传感器系统及电动伺服阀等组成；控制台由加载控制、数据采集及信号处理三大模块构成，具体包括上位机、NI PXIe机箱(RT控制器、数据采集卡及以太网卡)及PMSM驱动器等元件；配电柜则由主母线、制动电阻及可编程电源等电器元件组成。

ELLS主要由PMSM、转矩转速传感器、波纹管联轴器、滚珠丝杠副、光栅尺、拉压力传感器及被加载电动伺服阀构成。PMSM具有功率因数高及响应快等特点[8]，因此选用PMSM为ELLS驱动单元，采用NSK大导程滚珠丝杠副作为ELLS的运动转换机构，应用Interface拉压力传感器实时测量ELLS输出直线力。

图1 ELLS结构

1.2 ELLS原理

基于LabVIEW和PXI总线来搭建ELLS，ELLS的上位机通过TCP/IP协议与实时控制器通信，且须完成实时数据采集、处理和输出功能，自动进行数据分析，完成电动伺服阀相应的测试报告。PMSM设定输出的转矩、转速及位置信号经转矩转速传感器传送至采集卡；滚珠丝杠副将PMSM的输出扭矩转化为直线力，拉压力传感器测得直线力并反馈给实时控制器，且同时光栅尺可测得ELLS实时加载位移，数据采集卡把采集到的这三组通道数据通过PXI总线传给主控制器处理，闭环处理后得到PMSM控制指令，该指令由以太网卡经EtherCAT通信协议发送至AKD驱动器，由AKD驱动器驱动PMSM完成加载任务。电动伺服阀的位移、力输出由上位机通过RS422通信卡控制。

在ELLS中，由图1可看出，PMSM系统与电动伺服阀系统机械固连，故PMSM加系统的转矩输出会与电动伺服阀的输出相互耦合，进而会影响ELLS加载精度。当PMSM无输入信号时，定义由电动伺服阀运动所引起ELLS的附加力为多余力[9]。

2 ELLS硬件架构

基于ELLS技术方案及工作原理，采用PXI总线搭建ELLS的硬件架构，ELLS硬件架构如图2所示。

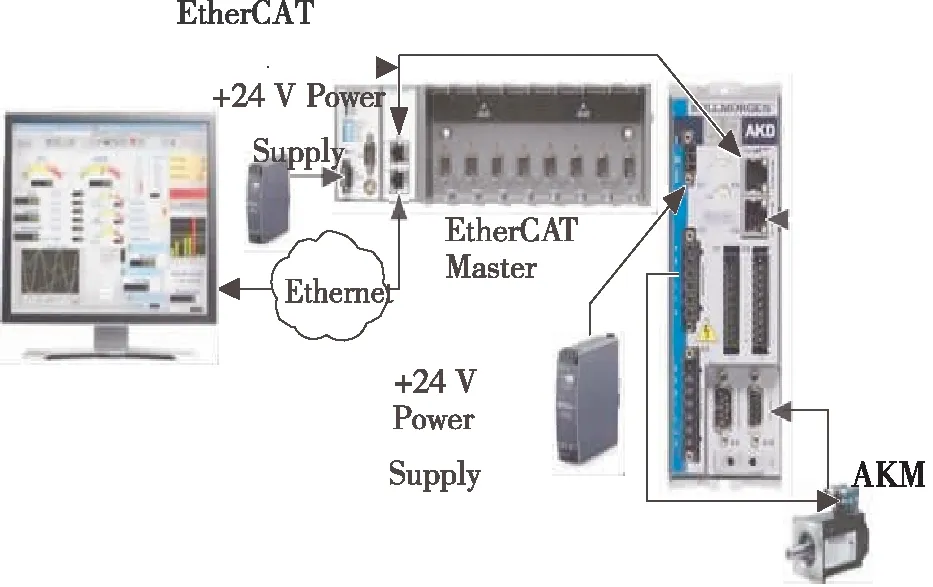
图2 ELLS硬件架构框图

在硬件选择上，采用PMSM作为ELLS的执行元件，采用大导程、无侧隙、高刚度的滚珠丝杠副作为ELLS的运动转换元件。基于系统技术要求，根据丝杠的导程、传动效率及转动惯量进行选型计算，选定NSK型号为LPFC 2525-6(P)的滚珠丝杠；基于伺服电机的最大转矩、转速及功率，选定型号为AKM53H-310VDC的Kollmorgen电机。

ELLS为典型的实时性测控系统，选用NI的PXI模块化平台来搭建ELLS。根据实时性的要求，采用NI PXIe-8840RT控制器，并安装RealTime模块。并选用机箱NI PXIe-1071搭载控制器，采用PXIe-6341数据采集卡，选用NI PXI-8231以太网卡以实现与AKD驱动器之间的通信。

3 ELLS数学模型

ELLS采用PMSM加滚珠丝杠的形式对电动伺服阀进行直线加载，而中间环节会影响ELLS性能，故将PMSM输出转矩视为由阻尼负载、惯性负载及弹性负载构成，其平衡方程为[10]：

(1)

式中，JL为负载的转动惯量；BL为阻尼常数；KL为弹性刚度常数；θL为丝杠角位移；θm为PMSM输出角位移。

由滚珠丝杠副运动模型[11]，且不考虑丝杆正反转效率、摩擦，则PMSM输出转矩近似为丝杠轴转矩，可得加载力与丝杠轴转矩的关系、丝杠角位移与电动伺服阀输出位移的关系分别为[12]：

(2)

式中，F为加载力；r为丝杠半径；λ为丝杠螺纹升角；L1为电动伺服阀输出位移；P为丝杠导程。

在理想情况下，基于PMSM在d-q轴系下模型方程[9]，且综合式(1)～式(2)，得ELLS传递函数为：

F=G1uq-G2L1

(3)

其中，

(4)

(5)

G3={(Lms+Rm)[(Jm+JL)s2+(Bm+BL)s+KL]+KtKes}rtanλ

(6)

式中，Kt为电磁转矩常数；uq为PMSM定子在q轴上的电压；Rm为定子的绕组电阻；Lm为电感常数；Ke为反电动势常数；Bm为电机阻尼常数；Jm为PMSM转动惯量。

ELLS控制结构图如图3所示。图3中，Tm为电磁转矩，ωm为PMSM转子角速度，TL为PMSM输出转矩。

图3 ELLS控制结构图

4 ELLS控制器设计

为提高ELLS加载精度，采用三闭环控制的闭环结构，如图4所示，图中：F*为指令力；Gω(s)为角速度补偿控制；Gp(s)为位置环控制；Giq(s)为电流环控制；GF(s)为力外环控制。基于复矢量PI控制的电流内环能够使PMSM电流准确地跟踪指令信号，位置内环Gp(s)与力外环GF(s)均应用PID控制。

图4 ELLS复合控制结构

在ELLS中，电流环控制器能够影响PMSM实际电流跟踪的快速性、准确性，且加载电机的电流环设计好坏直接影响负载力/力矩外环的复杂程度。

(7)

(8)

式中，KCP、KCI相应为PI控制器的比例和积分常数。

图5 电流环复矢量PI控制框图

由图5得复矢量PI控制的传递函数：

(9)

由式(9)可知，PI控制器中参数KCP及KCI对电流环交直轴耦合项补偿能力起着决定作用。当已知PMSM的电阻Rm和电感Lm时，可合理调节复矢量PI控制器参数KCP及KCI，使KCP/KCI=Lm/Rm成立，故可与d-q轴系的复矢量极点相消除[14]。在不考虑PMSM非线性因素及电流采样延时等情况下，将式(9)简化为式(10)，当KCω取较大值，可使复矢量PI控制器有良好的动态跟踪性能。

(10)

式中，KCω=KCP/Lm，KCω为电流环的开环截止频率。

5 实验验证

5.1 实验条件

为验证基于LabVIEW和PXI所搭建的ELLS的有效性，对自主研制的ELLS进行了调试；为验证所提控制方法能否有效满足ELLS指标要求，对ELLS进行了信号跟踪实验，试验台及控制台如图6所示。实验中，各控制器参数如下所示，Gp(s)：P1=1.32，I1=0.61，D1=0.02；GF(s)：P2=1.38，I2=0.89，D2=1.01；Giq(s)：KCP=4.1，KCI=450，KCω=1000。

(a) ELLS控制台

1.PMSM 2.转矩转速传感器 3.滚珠丝杠副 4.拉压力传感器 5.电动伺服阀(b) ELLS试验台图6 ELLS控制台及试验台

5.2 信号跟踪实验

基于LabVIEW图形化编程和MATLAB编程，编写了测控软件，并进行ELLS信号跟踪实验，信号跟踪曲线如图7所示。电动伺服阀设置幅值为3mm、频率为2Hz和5Hz的正弦信号为驱动指令信号，PMSM设置幅值为2000N、频率与扰动信号相同的正弦信号为加载指令信号。

对于被测电动伺服阀，其控制输出为位移，采用ELLS测试其输出力，以检验其推力是否满足在姿轨控发动机中的要求。ELLS初期调试，实验时间较短。在图7中，标有Force_Setpoint、Force_Feedback及Force_Error的曲线分别为设定加载曲线、加载反馈曲线及为误差曲线。由图7a，当电动阀输出频率为2Hz时，测得反馈曲线正峰值为2106.06N，反峰值为-2124.34N，相位为-8.01°，定义反馈值与设定值的比为加载精度，加载精度为93.783%，可见ELLS加载效果较好；当电动阀输出频率为5 Hz时，测得反馈曲线正峰值为2184.90N，反峰值为-2174.48N，相位为-8.83°，加载精度为90.755%。工程中常用指令信号与反馈信号的相位差小于10°、幅值差小于±10%来衡量ELLS性能，称之为“双十指标”[15]。总之，力外环和位置内环有效补偿电动阀的主动输出，基于复矢量PI的电流环有效增强了PMSM电磁转矩的控制能力，反馈曲线与设定曲线的相位差均小于10°，幅值误差也在10%以内，较好地达到了“双十指标”，有效地测试了此电动伺服阀能够满足2000 N的实载推力。

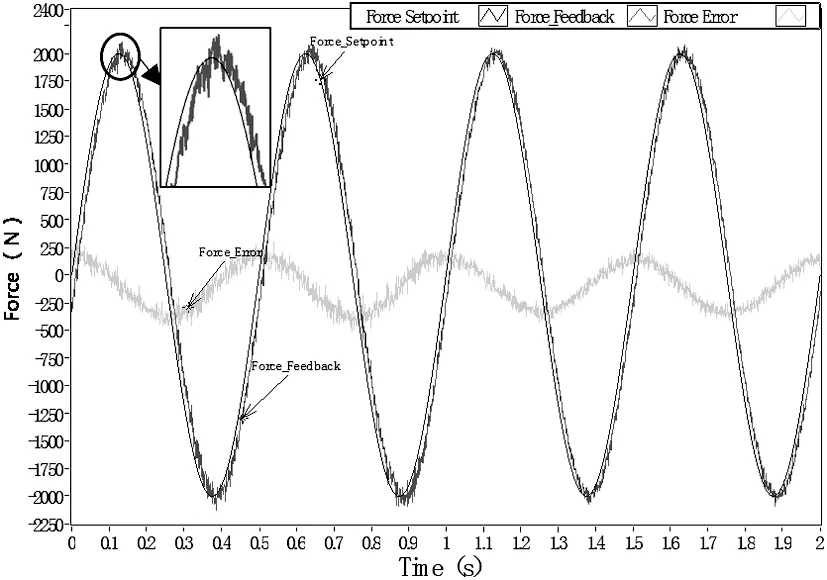
(a) 扰动信号为3 mm/2 Hz时的ELLS信号跟踪结果

(b) 扰动信号为3 mm/5 Hz时的ELLS信号跟踪结果图7 ELLS正弦信号跟踪曲线

6 结论

为测试某型电动伺服阀，设计了一种基于LabVIEW和PXI总线的电动直线加载系统(ELLS)；在机械结构上，采用PMSM加精密滚珠丝杠副的驱动形式。针对直线加载扰动更难抑制的特点，采取一种基于电流内环、位置内环和力外环的三闭环控制方法，并在电流内环中采用基于复矢量PI控制的电流耦合补偿方法。在构建的ELLS试验系统上进行信号跟踪实验，实验结果表明ELLS有效地测试了电动伺服阀的输出推力，并且ELLS达到了90%以上的跟踪精度，有效地抑制了多余力。

[参考文献]

[1] 张卫东,李力,张茂森,等.基于虚拟仪器和PXI总线的电磁阀控制系统研制[J].火箭推进,2015,41(1): 112-116.

[2] Wang Chengwen,Jiao Zongxia,Wu Shuai,et al.An experimental study of the dual-loop control of electro-hydraulic load simulator(EHLS)[J].Chinese Journal of Aeronautics, 2013, 26(6): 1586-1595.

[3] 杨波,程龙.提高电动加载系统输出平滑的CMAC复合控制[J].北京航空航天大学学报,2013,39(6): 723-727.

[4] 杨雪松,李长春,延皓,等.基于矢量匹配的扰动力矩消除方法[J].兵工学报,2016,37(2):348-356.

[5] 牛国臣,王巍,宗光华.基于迭代学习的电动负载模拟器复合控制[J].控制理论与应用,2014,31(12):1740- 1747.

[6] 周明广,于云峰,闫杰.直线舵机加载台控制系统建模与设计[J].测控技术,2011,30(6):53-56.

[7] 闫淑群,黎玉刚,母勇民,等.基于PXI总线的导弹自动测试系统设计[J].计算机测量与控制,2011,19(8): 1925-1929.

[8] 吕帅帅,林辉,樊明迪.电动加载系统多闭环复合控制[J].电机与控制学报,2015,19(9):16-21.

[9] 王哲.被动式力矩伺服系统加载策略研究[D].哈尔滨:哈尔滨工业大学,2015.

[10] Sebastian,Abu.Design methodologies fot robust neon positioning[J].IEEE Transactions on Control Systems Technology， 2005:868-876.

[11] 濮建荣.行星滚柱丝杠副接触、摩擦与工作特性的理论与试验研究[D].南京:南京理工大学,2015.

[12] 葛邵鹏程,范元勋.直线运动机构电动加载测试系统建模与仿真分析[J].组合机床与自动化加工技术,2016(9):91-94.

[13] Briz F,Degner M W,Lorenz R D.Analysis and Design of Current Regul Using Complex Vectors[J].IEEE Transactions on Industry Applications,2000,36(3):817- 825.

[14] 郭希铮,游小杰,王晓丹.永磁同步电机电流调节器动态特性改进方法分析[J],电力自动化设备,2011, 31(6):39-44.

[15] 焦宗夏,华清,王晓东.负载模拟器的评价指标体系[J].机械工程学报,2002,38(11):26-30.