行星滚柱丝杠螺纹误差对啮合状态影响分析

程 远，范元勋

(南京理工大学 机械工程学院，南京 210094)

0 引言

行星滚柱丝杠是一种将螺旋运动转化为直线运动的装置，由于其没有自锁能力，也可将直线运动转换为旋转运动。行星滚柱丝杠具有承载能力强、刚度大、效率高以及寿命长等优点。目前，主要应用在航空航天、精密机床、工业机器人及医疗器械等领域[1]。

受加工制造误差的影响，装配后的行星滚柱丝杠各零件之间的啮合状态，即啮合干涉量或啮合间隙量偏离预先设定值，在啮合区出现间隙过大或过度的干涉现象。间隙过大会导致行星滚柱丝杠传动精度降低[2]；过度的干涉会导致行星滚柱丝杠初期剧烈的摩擦磨损[3]，降低丝杠传动效率及使用寿命[4]。

在行星滚柱丝杠啮合分析方面，文献[4-5]建立了啮合运动方程，对初始啮合点及相对滑动速度进行了分析。文献[6]通过将螺旋面进行离散，对啮合间隙进行了计算。文献[7]通过建立行星滚柱丝杠螺纹螺旋曲面方程，建立行星滚柱丝杠啮合方程，并进行了求解。但以上分析都是对理论螺旋面进行的分析，未对行星滚柱丝杠啮合干涉及间隙情况进行分析，更没有考虑加工误差对行星滚柱丝杠啮合状态的影响。

本文基于行星滚柱丝杠结构特点，建立行星滚柱丝杠空间啮合方程，采用数值算法对空间啮合方程进行求解，计算出零侧隙啮合条件下行星滚柱丝杠丝杆和螺母螺纹的几何中径。在此基础上，分析了行星滚柱丝杠螺纹几何中径误差，螺距误差，牙型半角误差，滚柱型面圆弧半径误差对行星滚柱丝杠啮合状态的影响。结果表明，几何中径，螺距误差对啮合状态的影响较大，滚柱型面圆弧半径对啮合状态的影响很小。误差分析结果与实际生产情况一致，验证了方法和分析结果的有效性。

1 行星滚柱丝杠结构

行星滚柱丝杠有多种形式，考虑到分析的典型性，本文以标准型行星滚柱丝杠为研究对象。其主要由丝杆、滚柱、螺母、齿环、保持架以及挡圈等组成[8]，如图1所示。当丝杠运动时，丝杆绕轴线转动，滚柱绕丝杆轴线做行星运动，螺母直线运动。

图1 行星滚柱丝杠结构

通常情况下，为获得良好的接触状态，丝杆、螺母的轴向截面内牙型轮廓为直线，滚柱轴向截面牙型轮廓为圆弧形，从而获得点接触形式。行星滚柱丝杠牙型轮廓如图2所示。

图2 牙型轮廓

图中，P0表示螺距，β为型面牙型半角，Rr为滚柱型面圆弧半径。

2 空间啮合方程

2.1 坐标系的建立

根据行星滚柱丝杠的结构特点，建立如图3所示的空间坐标系。主要有固定坐标系(Oxyz)、滚柱坐标系(ORxRyRzR)、滚柱截面坐标系(Orxryrzr)、丝杆截面坐标系(Osxsyszs)、螺母截面坐标系(Onxnynzn)。

图3 啮合接触分析坐标系

图中，rs、rr、rn分别表示滚柱、丝杆和螺母螺纹中径半径，a为滚柱轴线与丝杆轴线之间的距离。

2.2 螺旋面方程

考虑到对称性，仅对行星滚柱丝杠滚柱、丝杆以及螺母一侧螺旋曲面建立参数方程[9]。

在滚柱截面坐标系Orxryrzr中，滚柱左侧母线上一点M在滚柱坐标系ORxRyRzR中的参数方程为：

(1)

式中，ur为角参变量，xrM、yrM、zrM为M点在滚柱坐标系中坐标。

固定坐标系Oxyz内，滚柱母线绕滚柱轴线做螺旋运动所形成的螺旋曲面参数方程为：

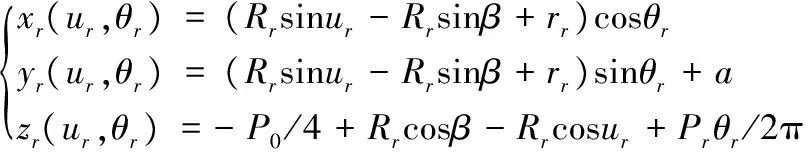
(2)

式中，θr为滚柱母线绕滚柱轴线zr的转角，Pr为滚柱导程。

为获得零侧隙啮合接触状态，将行星滚柱丝杠丝杆、螺母螺纹几何中径设为未知参数。丝杆右侧母线绕丝杆轴线z形成的螺旋曲面可以分别表示为：

(3)

式中，θs为丝杆右侧母线绕丝杆轴线z的转角，Ps为丝杆导程，us为参变量。

同理，螺母右侧母线绕螺母轴线z形成的螺旋曲面可以分别表示为：

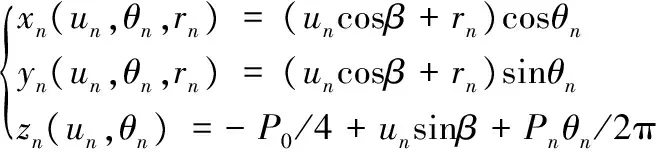
(4)

式中，θn为丝杆右侧母线绕丝杆轴线z的转角，Pn为丝杆导程，un为参变量。

2.3 啮合方程

根据空间啮合原理，行星滚柱丝杠滚柱与丝杆滚柱与丝杠满足连续啮合的条件为[10]：

vrs·n=0

(5)

式中，vrs为啮合点相对运动速度，n为啮合点螺纹螺旋面法向矢量。

(6)

式中，u为ur或us，θ为θr或θs。

因螺旋面任意点切向矢量与该点处法向矢量垂直，有vr·nr=vs·ns=0。则当二者在任一点有公法线时，满足啮合条件。nr=kns，k为比例系数。

由此，滚柱与丝杆的啮合方程为：

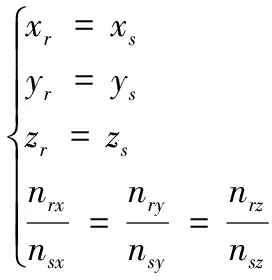
(7)

求解上述方程，可解得(ur,θr,us,θs,rs)，最终获得滚柱、丝杆啮合点坐标P(Px,Py,Pz)和丝杆螺纹几何中径rs。

同理得滚柱与螺母的啮合方程为：

(8)

求解方程，可解得(ur,θr,un,θn,rn)，最终获得滚柱、螺母啮合点坐标Q(Qx,Qy,Qz)和螺母螺纹几何中径rn。

2.4 啮合计算

行星滚柱丝杠啮合方程为非线性方程组，可以通过牛顿-拉弗逊算法对其进行计算[11]。

以某一规格的标准型行星滚柱丝杠为例，对行星滚柱丝杠啮合方程进行计算。行星滚柱丝杠理论参数如表1所示，此参数满足行星滚柱丝杠运动学方程[8]。

表1 行星滚柱丝杠理论几何参数

基于表1参数及啮合方程，分别求出零侧隙啮合情况下行星滚柱丝杠丝杆、螺母螺纹几何中径rs、rn。计算结果如表2所示。

表2 滚柱与丝杆和螺母实际啮合中径值

以上实际结果表明，在按行星滚柱丝杠运动学方程进行参数计算所得到的理论参数设计行星滚柱丝杠时，滚柱与螺母之间干涉很小，工程上可以忽略不计，但滚柱与丝杠之间存在严重的干涉问题。

3 螺纹型面误差分析

在实际加工过程中，行星滚柱丝杠螺纹型面与理论参数存在偏差，本节以表1行星滚柱丝杠实际参数为例，从螺纹几何中径误差，螺距误差，牙型半角误差，滚柱型面圆弧半径误差等四个方面对啮合状态的影响进行分析。

3.1 螺纹几何中径误差

行星滚柱丝杠螺纹几何中径误差对行星滚柱丝杠的啮合状态的影响如图4所示。图中，啮合点轴向间隙量正值表示存在啮合间隙，负值表示存在啮合干涉。所分析的滚柱、丝杆以及螺母的几何中径直径误差在±0.1mm范围内。

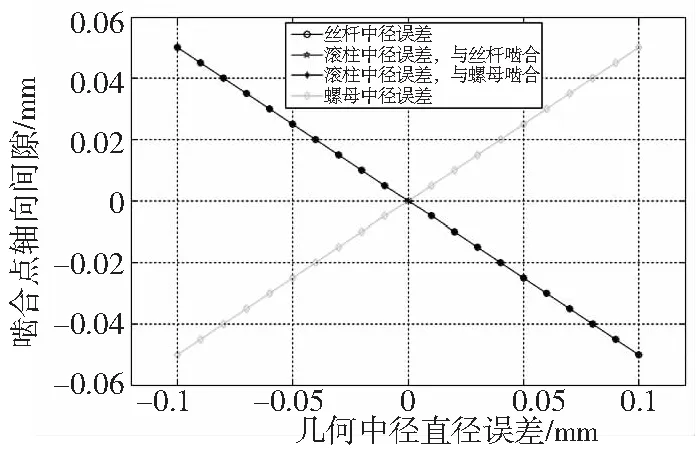
图4 几何中径误差分析

从图4可见，啮合间隙量与滚柱、丝杆以及螺母的几何中径误差成线性关系。滚柱、丝杆螺纹几何中径误差值增大，啮合点轴向间隙量减小；螺母螺纹几何中径值增大，啮合间隙量增大。行星滚柱丝杠螺纹几何中径误差对行星滚柱丝杠啮合状态有明显影响。

3.2 螺距误差

行星滚柱丝杠螺距误差对行星滚柱丝杠的啮合状态的影响如图5所示。其中，由于行星滚柱丝杠螺距值一般较小，误差值也较小。所分析滚柱、丝杆以及螺母的螺距误差在±0.05mm范围内。

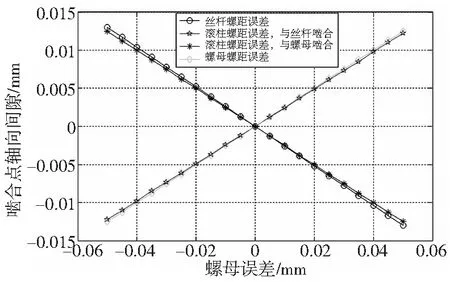
图5 螺距误差分析

从图5可见，啮合点轴向间隙量与滚柱、螺母、丝杆螺距误差成线性关系。丝杆螺距误差值增大，滚柱与丝杆轴向间隙减小；滚柱螺距误差值增大，滚柱与丝杆啮合轴向间隙增大，滚柱与螺母啮合轴向间隙减小；螺母螺距误差值增大，滚柱与螺母啮合轴向间隙增大。螺距误差对啮合点轴向间隙量的影响略小于几何中径，依然很大，工程中不可忽略。

3.3 牙型半角误差

行星滚柱丝杠牙型半角差对行星滚柱丝杠的啮合状态的影响如图6所示。其中，滚柱、丝杆以及螺母的牙型半角误差在±0.5°范围内。

图6 牙型半角误差

从图6可见，啮合间隙量与滚柱、丝杆和螺母的牙型半角误差均成非线性关系，类似于二次抛物线。滚柱和螺母误差的啮合间隙量抛物线顶点在误差零点；丝杆误差啮合间隙量抛物线顶点在误差为正的某一点。当滚柱与螺母牙型半角存在偏差时，均会产生啮合干涉；丝杆的牙型半角误差为负时，产生啮合干涉，误差为正时，存在啮合间隙，且间隙先增大后减小，误差大于一定值时存在啮合干涉。丝杆牙型半角误差对啮合状态的影响大于滚柱和螺母牙型半角误差，牙型半径对啮合状态的影响较小。

3.4 滚柱型面圆弧半径误差

行星滚柱丝杠滚柱圆弧半径对行星滚柱丝杠的啮合状态的影响如图7所示。所分析滚柱圆弧半径误差在±0.5mm范围内。

从图7可见，滚柱与丝杆啮合点轴向间隙量与滚柱型面圆弧半径误差近似成线性关系，误差值增大，啮合间隙量减小；滚柱行星圆弧半径对滚柱与螺母之间啮合间隙量无影响。

图7 滚柱型面圆弧半径误差

3.5 小结

分析结果表明，在行星滚柱丝杠螺纹几个参数中：螺纹几何中径误差与啮合间隙量在同一数量级上，对啮合点轴向间隙量的影响最大，螺距误差次之，误差会导致啮合干涉或间隙量过大，工程中需重点关注；牙型半角误差引起的啮合间隙量在10-4mm数量级，滚柱型面圆弧半径误差对啮合间隙量在10-9mm数量级，工程中均可以忽略。

在实际生产加工过程中，螺纹几何中径误差和螺距误差对啮合干涉或啮合间隙影响明显。误差分析结果与实际生产加工情况一致，证明方法和分析结果有效。

4 结论

本文通过建立行星滚柱丝杠螺旋型面空间啮合坐标系以及空间啮合方程，分析了行星滚柱丝杠螺纹螺旋面参数误差对行星滚柱丝杠啮合状态的影响，得出如下结论：

(1)在按行星滚柱丝杠运动学关系对行星滚柱丝杠螺纹参数进行设计时，滚柱与丝杆之间存在严重的干涉问题，实际丝杆螺纹几何中径值应小于运动学方程计算所得理论值。

(2)行星滚柱丝杠螺纹几何中径及螺距误差对啮合状态影响明显，牙型半角误差、滚柱型面圆弧半径误差对啮合状态影响较小，工程上可以忽略。

[参考文献]

[1] 刘更，马尚君，佟瑞庭,等.行星滚柱丝杠副的新发展及关键技术[J].机械传动，2012，36(5)：103-108.

[2] Lemor P C. The roller screw, an efficient and reliable mechanical component of electro mechanical actuators[C]. Energy Conversion Engineering Conference, 1996. Iecec 96. Proceedings of the, Intersociety. IEEE, 2002:215-220.

[3] Jones M H, Velinsky S A. Kinematics of Roller Migration in the Planetary Roller Screw Mechanism [J]. Journal of Mechanical Design, 2012, 134(6):579-580.

[4] Velinsky S A, Chu B, Lasky T A. Kinematics and Efficiency Analysis of the Planetary Roller Screw Mechanism[J]. Journal of Mechanical Design, 2009, 131(1):011016.

[5] Jones M H, Velinsky S A. Contact Kinematics in the Roller Screw Mechanism[C]. ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2012:451-459.

[6] 赵英, 倪洁, 吕丽娜. 滚柱丝杠副的啮合计算[J]. 机械设计, 2003, 20(3):34-36.

[7] 付晓军，刘更，马尚君,等.行星滚柱丝杠副螺旋曲面啮合机理研究[J].机械工程学报，2016，52(3)：26-33.

[8] 靳谦忠, 杨家军. 行星式滚柱丝杠副的运动特性及参数选择[J]. 制造技术与机床, 1998(5):13-15.

[9] 吴序堂.齿轮啮合原理[M].西安：西安交通大学出版社，2009.

[10] 徐强, 王水铭, 赵国平,等. PWG型差动丝杠的啮合干涉分析与消除[J]. 组合机床与自动化加工技术, 2015(9):107-109.

[11] 陈宝林. 最优化理论与算法[M]. 北京:清华大学出版社, 2005.

(编辑李秀敏)