数控双驱二维工作台的控制方法与联合仿真研究*

卢 红，毛尔东，范 维

(武汉理工大学 机电工程学院，武汉 430070)

0 引言

随着现代制造业的发展，数控装备正向着高速、高精、高效等方向快速发展。进给系统作为数控装备的控制对象和执行单元，其系统结构和控制精度将直接影响装备的工作性能[1]。传统的进给驱动方式一般是采用单电机加单丝杠驱动方式，这样做往往很难保证轴驱动力能够精确作用于运动部件重心，进而影响机械装备的精度和使用寿命。数控双驱二维工作台作为一种新型的数控二维工作台，采用双电机+双丝杠的驱动方式，使丝杠直径减小的同时也使传动合力作用点移至工作台的几何中心上，实现了机床速度、精度的提高并能大幅提升机床使用寿命，其进给模型如图1所示。但双驱同步结构中的电机、丝杠等部件从出厂起即存在特性上的差异，加上双电机间的强机械及电磁耦合的影响，使双电机的输出不可能完全一致，产生同步误差，进而导致双驱工作台发生扭斜等问题，最终导致工作台的精度难以保证。因此，对高速高精的数控加工系统的双驱同步控制方法的研究具有重大意义。

图1 数控双驱二维工作台

为了提高双驱进给系统的同步精度，国内外学者从上位机运动控制方法的角度对双驱同步控制问题进行了大量的研究。在早期，日本学者Masatoshi Nakamura 等在两自由度机械手的主从跟随位置同步控制研究基础上，提出了“主从双模同步控制”算法，即利用主从控制方式中主动轴有较好的抗干扰能力，根据干扰力矩大小进行主从轴实时切换[2]；国内学者李连升提出了加入差点流负反馈的方法保证两个电机的电流一致，在此基础上陈庆伟又提出了一种差速负反馈的控制器，断开从动电机的速度环，由主动电机速度补偿后将电流信号直接加给电流环[3]，这两种控制方法都是采用串联控制，即一个或多个电机跟踪主电机的电流、速度或位置；与其相对应的另一种方法叫并联控制，采用两套相同的伺服系统，两轴相互独立。 Koren在上世纪80年代初首次提出交叉耦合的控制方法，通过附加速度差或位置差的反馈信号实现对轴间位置偏差的补偿； Tomizuka 等基于两直流电机并行驱动结构，设计了自适应扰动补偿和自适应前馈控制技术，将自适应技术引入交叉耦合控制器； Sun 等将自适应前馈控制技术拓展到位置同步控制中，提出自适应耦合控制策略，将位置误差和同步偏差反馈一起引入到控制器和参数适配器上，实现了两机器人的协同控制[4]。

就目前的发展来看，基本的控制方式有串联控制，并联控制以及交叉耦合控制。串联控制中，如果从动轴受到干扰，主动电机则无法收到反馈，同样，并联控制中，其中一个电机受到扰动另一个也无法得知。而交叉耦合控制实时地计算了多种干扰因素造成的同步误差，因此交叉耦合控制策略成为了双驱同步控制策略应用的主流技术，很多控制策略都是基于交叉耦合控制策略的基础上逐渐演化来的。这一控制策略实现起来较为简单，衍生技术的积累也最多，应用最广泛，可以满足多样化的控制需求[5-6]。

在交叉耦合控制的基础上，结合前馈技术提出基于扰动补偿的交叉耦合同步控制方法改善系统响应特性和精度。利用ADAMS和Matlab进行机电联合仿真，通过与实验结果的轮廓轨迹对比验证联合联合仿真的可靠性。并在仿真过程中给定控制信号，对比分析传统交叉耦合控制方法和基于扰动补偿的交叉耦合控制方法的控制效果，最后通过实验验证。结果表明机电联合仿真的结果可信度较高，为工作台的设计提供更加可靠的仿真方法，而基于扰动补偿的交叉耦合控制方法的同步控制效果更优，改善了双驱进给系统的同步控制精度。

1 双驱同步控制方法研究

1.1 基于扰动补偿的交叉耦合同步控制

基于扰动补偿的交叉耦合同步控制是在并行控制的基础上,考虑了轴间控制的耦合和协调关系,通过引入速度差或位置差作为附加反馈信号实现对轴间位置偏差的协调和补偿,从而获得较好的轴间同步性能。传统的交叉耦合控制策略示意图如图2所示，在该控制方式下,同步性能的优劣关键取决于补偿算法,应用不同算法,轴间同步性能将有所不同。基于单轴扰动补偿的改进交叉耦合控制策略，在扰动发生时，补偿控制器及时动作，可以很好地抑制被控制量的动静态偏差，图3为基于扰动补偿的改进交叉耦合控制策略示意图。

图2 常规交叉耦合控制

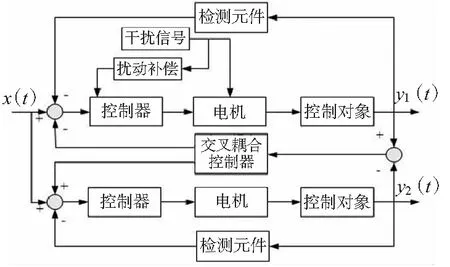
图3 基于扰动补偿的改进交叉耦合控制

1.2 单轴伺服驱动系统建模

要建立伺服系统的模型，首先对交流伺服电机进行建模，交流伺服电动机不仅具有电磁惯性和机械惯性，而且其调节特性和机械特性是非线性的，同时考虑到电磁惯性与机械惯性相比相对较小，因此采用小偏差线性化方法进行动态分析。为了简化计算，假定电机为空载，电机运动方程为[7]:

(1)

式中，J—转动惯量，M—电磁转矩，Ω—旋转角速度。

在初始为零的条件下，对式(1)作拉式变换，可得：

M(s)=J×s×Ω(s)

(2)

设Ω(t)是控制电压UK和转矩M的函数，则有：

(3)

在工作点附近的小范围内，∂Ω/∂UK和∂Ω/∂M可视为常数，在初始为零的条件下，对式(3)作拉式变换，可得：

(4)

将式(2)带入式(4)得：

(5)

因此，交流伺服电机的传递函数G(s)为：

(6)

式中，Tm=-∂Ω/∂M是伺服电机常数，等于机械特性率与转动惯量的乘积，Kc=∂Ω/∂UK为增益系数，是电机调节特性在工作点出的斜率。而本系统所选用的是德国倍福公司的AM8531型电机，根据其固有参数，可得Tm=7.26087，Kc=4347.82609。

根据以上公式，加入位置和电流环调节器传递函数模块，即可得到该数控双驱二维工作台进给系统的电机-控制器数学模型，内环和外环均采用PI控制策略，经简化后其传递函数分别为G1(s)=1/(Kis+1)，G2(s)=Ks(τs+1)/τss，其中Ki为电流环时间常数，Ks为速度环比例参数，τs为速度环的积分时间常数。

1.3 单轴扰动补偿控制器的设计

为了提高砂轮修形机工作台进给过程双电机的同步精度，从提高单电机伺服系统本身抑制负载扰动性能的角度出发，采用基于扰动补偿的伺服系统。其原理图可简化如图4所示。

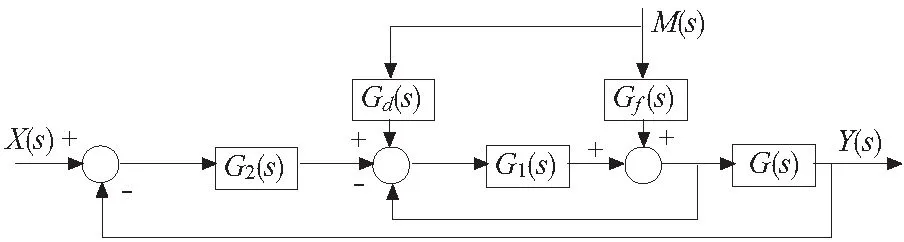
图4 扰动补偿原理图

图4所示的前馈—反馈控制系统，系统对扰动的传递函数为：

而在单纯前馈控制下，系统对扰动的传递函数为:

由此可见，通过对比前馈—反馈控制系统与单纯的前馈控制系统的传递函数，扰动量的影响为原来的1/[1+G(s)×G1(s)×G2(s)]，扰动影响减少了，同时增加了反馈调节能力。

1.4 双轴伺服驱动系统建模

在对单轴进给系统进行建模后，需要确定双电机控制模型的控制策略。运用机电联合仿真技术对基于扰动补偿的交叉耦合控制策略和传统交叉耦合控制策略分别进行仿真实验，并对比单独在Simulink中仿真以及最后实验数据。控制策略的系统控制框图如图5、图6所示。

图5 传统交叉耦合控制框图

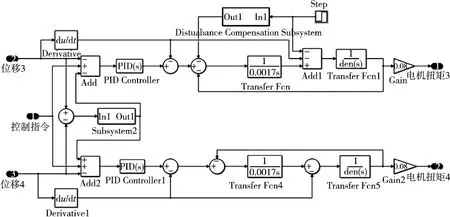
图6 基于扰动补偿控制框图

2 机电联合系统仿真平台实现

基于多领域的联合建模和仿真技术能够很好解决控制系统和机械系统在设计过程中交互不足的问题，为对进给驱动系统的研究提供了一种新的方法。与过去机械系统和控制系统分别孤立进行仿真的方式不同，机电联合仿真能够更准确地模拟实际负载和控制效果，省去了建立负载数学模型的过程，提高了仿真效率[8-9]。联合仿真可分为4个步骤[10]：①建立数控双驱二维工作台进给驱动系统的机械模型，添加约束；②建立系统的控制变量接口，定义输入和输出；③建立系统的控制模型；④联接控制系统与机械传动模型，进行仿真实验，对比工作台在不同双驱控制方法下的动态性能。

2.1 虚拟样机模型的建立

采用Solidworks软件对数控双驱二维工作台进行实体建模，在此将工作台台面直接导入ADAMS中，简化键槽和螺纹等一些不影响精度的细节信息。但其他零部件的结构位置较为复杂。例如，在Solidworks中建立的伺服电机仅为一个模型，其内部结构均为简化结构，如果将其直接导入ADAMS软件便无法对其添加旋转副等约束，因此对于整个装置中的伺服电机、滚珠丝杠及螺母，导轨滑块以及滚珠丝杠轴承和与电机相连的联轴器均在ADAMS软件中进行建模。建立的虚拟样机模型如图7所示。

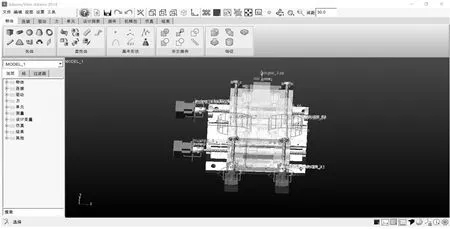
图7 虚拟样机模型

2.2 定义ADAMS的输入与输出

这里，模型的输入为工作台X向与Z向4个电机轴的扭矩，输出为螺母的位置，X向平台的位置、速度和加速度，Z向平台的位置、速度和加速度。将ADAMS的工作目录设定为目标路径，执行Control模块中的Export命令，导出一个Matlab的可执行文件(.m)、一个ADAMS的命令文件(.cmd)和一个ADAMS的Solve的命令文件(.adm)，供联合仿真分析时使用[11]。

2.3 控制系统协同模型的建立

在Matlab/Simulink下建立前文所述的控制系统模型，并将在ADAMS中构建的机械模型导入Simulink中成为一个模块。在Matlab中建立数控双驱二维工作台机电联合仿真平台如图8所示。

图8 机电联合仿真平台

2.4 仿真和实验结果

为了验证联合仿真的可靠性，在采用传统交叉耦合的控制方式下将机电联合仿真结果与二维双驱工作台的X、Z向进给的轮廓轨迹在不同速度时进行对比分析。给定控制信号为工作台在X轴方向与Z轴方向的位移分别为，X方向正向移动40mm再反向移动40mm，Z方向先正向移动20mm再反向移动40mm再正向移动20mm。图9为基于倍福数控系统控制的二维工作台实物图。图10～图12为机电联合仿真与试验的轮廓轨迹对比。对应的速度从上至下依次为50mm/s,30mm/s,5mm/s，虚线是试验数据，实线是仿真数据。

图9 工作台实物图

图10 轮廓轨迹1

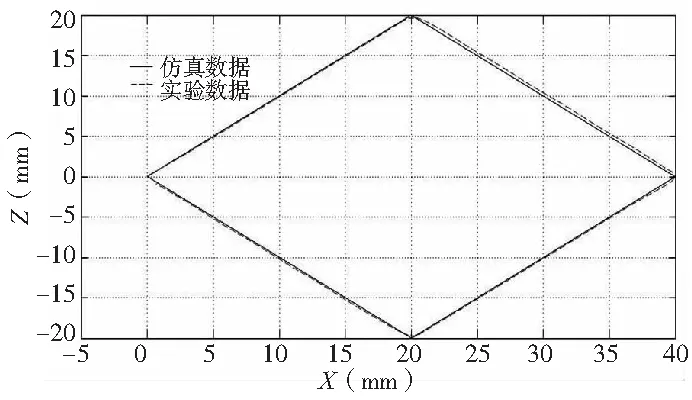
图11 轮廓轨迹2

图12 轮廓轨迹3

对比实验结果可以看出，在低速情况下，仿真结果和实验数据相差较小，虽然在高速进给的时候误差相对较大，但是轨迹和趋势仍然符合实际情况，因此联合仿真能够准确的反映工作台进给系统的动态特性，符合双驱二维工作台的实际工况，能对实际双驱二维进给的同步和轮廓轨迹的控制策略设计提供指导。

进一步进行仿真和实验，在基于扰动补偿的控制方式下，设定仿真时间为5s，给定控制信号同上，在移动过程中，进给速度为16mm/s。完成设置之后即可开始联合仿真，并分别得到工作台X方向与Z方向的位移，速度和加速度曲线，分别如图13～图14所示。进行实验前，下载安装 TE1400-Target-for-Matlab-Simulink， TE1400利用Simulink Coder 把 Simulink 中的模型生成实时 C/C++代码，并进一步导出自带输入输出接口的可供倍福数控系统控制软件TwinCAT3直接调用的TcCOM模块。完成导出后，在TwinCAT3的TcCOM Objects中添加生成的TcModule并配置输入输出。输入为控制指令及X轴和Z轴的位置反馈，输出为电机扭矩。为了提高测量精度，此系统在最外环添加了直接的位移检测元件，GIVI绝对式光栅尺：AGS-T01A-270-05V-B1-V-M04/R-C58，检测精度达±1μm。完成配置后用相同的控制信号，在现有的基于倍福数控系统控制的二维工作台上进行试验，得到两种控制方式下工作台两个方向位移、速度和加速度曲线如图15～图18所示。

联合仿真结果：

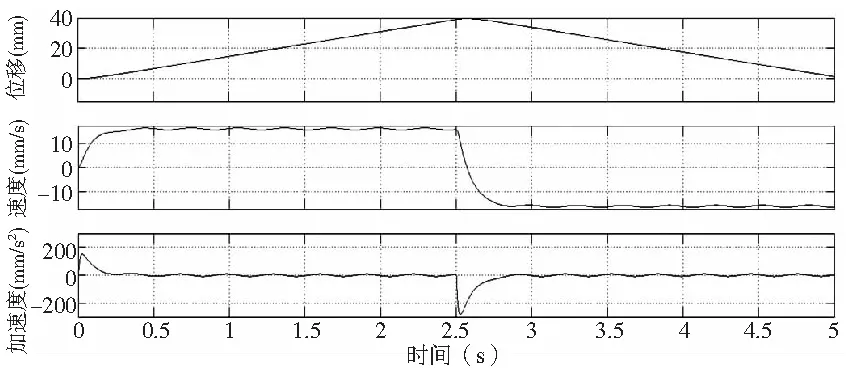
图13 基于扰动补偿控制X向

图14 基于扰动补偿控制Z向

试验结果：

图15 交叉耦合控制X向

图16 交叉耦合控制Z向

图17 基于扰动补偿X向

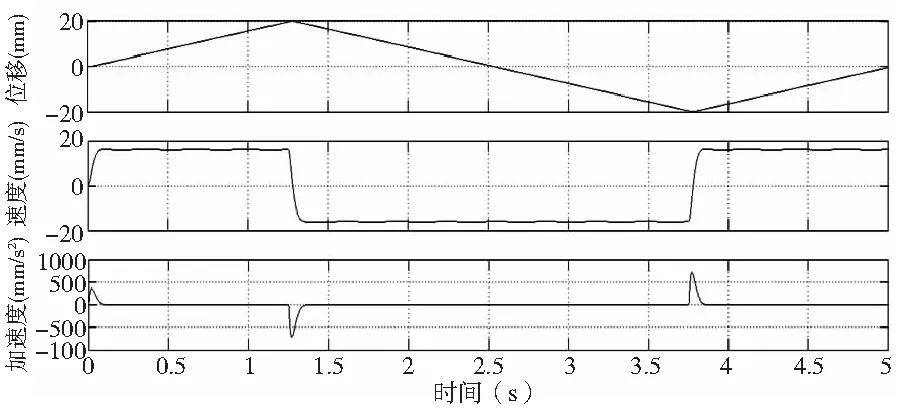
图18 基于扰动补偿Z向

从双驱二维进给试验结果中可以看出，相比于传统交叉耦合控制，工作台在基于扰动补偿的改进交叉耦合的双驱同步控制下，系统的运动轨迹轮廓误差较小，控制精度更高，速度曲线与加速度曲线最为平稳且在工作台在换向时，稳态响应时间较短，能及时做出响应。

3 结论

在研究了多种双轴同步控制策略的基础上，建立分析基于扰动补偿的改进交叉耦合双驱同步控制策略，结合ADAMS和Matlab软件搭建机电联合仿真平台。对比仿真和实验数据。表明基于扰动补偿的改进交叉耦合双驱同步控制策略拥有更好的控制精度，而机电联合仿真平台帮助我们避免了复杂的建模过程，降低了设计成本，为双驱二维工作台进给驱动方案的设计提供来了可靠的研究方法，也为提前发现问题、整定系统参数并对系统改进提供了依据。

[参考文献]

[1] 夏田，王志军，缑建文,等.基于重心驱动进给系统工作台动态性能分析[J].组合机床与自动化加工技术,2014

(9):109-112.

[2] Nakamura M, Yamanaka S. Dual mode synchronous positioning with switching of master-slave axes by using a torque signal for contour control of articulated robot arms [J]. Electrical Engineering in Japan,2001,37(11):1062.

[3] 陈庆伟，郭毓.双电机同步联动控制系统[J].南京理工大学学报,2005,29(s1):103-107.

[4] Sun Dong, Shao Xiaoyin, Feng Geng. A Model-free Cross-coupled Control for Position Synchronization of Multi-axis Motions: Theory and Experiments [J]. IEEE Transaction on Control Systems Technology,2007,15(2):306-314.

[5] 程颖.基于PMAC的双丝杠驱动同步运动控制研究和应用[D].武汉:华中科技大学,2011.

[6] 何王勇. 数控机床双轴同步控制技术研究[D].武汉:华中科技大学,2011.

[7] 丁文, 高琳, 梁得亮.永磁同步电机矢量控制系统的建模与仿真[J]. 微电机,2010,43(12): 66-71.

[8] 周奎，王文格,肖博.多轴鼓轮系统同步控制机电联合仿真研究[J].工程设计学报,2013，20(5):368-374.

[9] ANYU C，XILIANG D，SHUGEN H. Co-simulation study on EPS system based on ADAMS and MATLAB [C].Proceeding of Third International Conference on Measuring Technology and Mechatronics Automation ICMTMA. Shanghai:2011.

[10] 沈俊，宋健.基于ADAMS和Simulink联合仿真的ABS控制算法研究[J].系统仿真学报，2007,19(5):1141-1143,1160.

[11] 袁安富,沈思思,余莉,等.基于ADAMS和MATLAB的喷涂机器人运动仿真研究[J].组合机床与自动化加工技术,2014(8):44-48.

(编辑李秀敏)