基于多因素影响的数控铣床定位误差研究*

曾 超，王湘江

(南华大学 机械工程学院，湖南 衡阳 421000)

0 引言

在现代机械制造中，精密和超精密数控加工技术成为最重要的组成部分和研究方向，而数控机床的定位精度则是机床验收和测试的重要指标，同时，随着机床的使用，定位精度会逐渐降低[1-4]。所以，对数控机床定位误差的研究，显得尤为重要，国内外学者也做了一定的研究。Kwintarini W[5]总结了数控铣床定位精度的影响因素和现有加工技术的局限性 。Yang J[6]提出了一种轮廓误差的在线估计与控制方法，通过将轴分量反馈到各轴闭环伺服控制系统，轮廓误差减小了一半。JY Chen[7]利用球杆仪和激光干涉仪相结合的方法对影响数控机床加工精度的因素进行分析并补偿，提高了定位精度。Wang W[8]等通过检测不同温度下的定位误差，并利用牛顿插值的方法进行建模，得到误差补偿模型，而Chen T C[9]也在提出减小热误差是能有效提高机床精度的基础上研究开发了一种减少数控铣床热误差的补偿模块。陈芳[10]提出了一种基于3D测头和宏程序相结合的机床定位精度自动测量的方案，能在不增加昂贵设备的同时，有效地提高机床定位精度。可以看出大量的研究还只是基于理论分析或数学建模，缺乏在实际过程中的分析。

本文内容建立在大量的实验基础上，通过对比试验分析环境因素对定位误差测量的影响。同时，分别分析在进给速度、测量间距、加工时间的单因素影响下误差变化情况。最后通过在一定时间段内，多次测量定位误差，并绘制概率分布曲线，分析定位误差可靠度以及影响定位精度的原因。

1 试验装置介绍

试验研究设备是南华大学金工实习工厂的一台三轴数控铣床，型号为MVC850B，该机床3轴行程长度(x-y-z)为800mm-500mm-550mm。测量仪器是德国雷尼绍生产的LaserXL-30激光干涉仪，并带有配套的测量软件。图1为数控铣床定位误差测量装置。每次测量之前，启动机床先空运行1～2h，使机床达到相对平衡状态，激光器预热20min左右，使激光频率达到稳定状态，尽量减小周围环境的振动和干扰源[11-12]。

图1 数控铣床定位误差测量装置

采用激光干涉仪对数控铣床的定位误差进行测量，激光器发出激光束①，由分光镜分裂成反射光束②和发射光束③。这两束光分别经反射镜又反射到分光镜的同一位置，由分光镜进行调制后，把光束④传送到激光器中，从而使这两束光在激光探测器中产生干涉条纹。最后传送到安装有测量软件的计算机进行记录，得到误差数据。

2 环境参数对比试验分析

由于激光干涉仪是利用光电效应进行机床定位误差的测量，因此对工作环境十分敏感。为了保证激光测量的高精度，对实际工作的环境有严格的要求范围。环境控制的主要指标为空气温度、空气的相对湿度以及大气压力等。以上指标变化的综合结果将会引起空气折射率发生变化，从而导致波长的变化，最终引起测量误差[13-14]。

在标准环境状态下和通过对环境参数进行修正后的实际环境状态下分别测量X轴、Y轴定位误差，如图2、图3所示，测量时的实际环境参数与标准参数如表1所示。

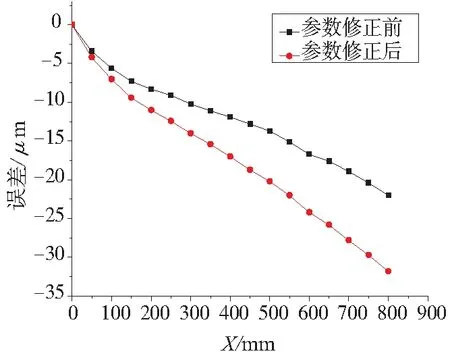
图2 X轴定位误差对比图

图3 Y轴定位误差对比图

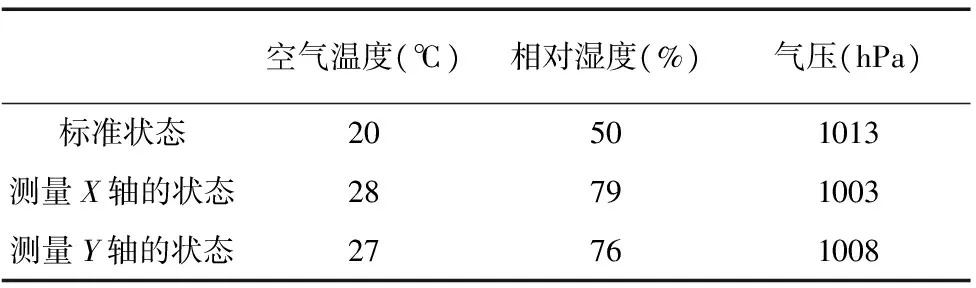
表1 环境参数表

根据Edlen经验公式，可以得到由环境引起的测量误差δ可以表示为：

δ=-0.929×10-6Δt-0.042×10-8Δf+0.269×10-8Δp

式中，Δt、Δf、Δp分别为温度、湿度、气压相对于标准状态的变化量。

由于环境参数修正前后的两次测量时间间隔较短，这里忽略机床温度变化的影响。通过计算可以得出理论上X轴、Y轴由环境引起的测量误差δx、δy分别为-7.6μm、-6.6μm。而根据图2、图3可知，通过直接测量的由环境引起的实际测量误差δx测、δy测分别为-9.8μm、-5.3μm。测量的数据与通过理论经验公式计算出来的数据相差不大，说明通过对环境参数的修正，可以得到更加较为准确的机床定位误差。而对以后实际加工时进行机床误差补偿时，消除由环境引起的测量误差有较为重大的意义。同时可以得到温度对测量误差的影响较大，其次是气压的影响，湿度的影响较小，可以忽略。

3 定位误差单因素分析

在大量的试验研究基础上，总结出在测量时进给速度，测量时的测距以及加工时间对测量定位误差的影响。以进给速度、测距、加工时间为变量因素，反向间隙误差和螺距累积误差作为响应输出。其中进给速度的变化范围为50mm/min～4000mm/min，测距分别以1mm、5mm、10mm、20mm、50mm、100mm进行测量，加工时间从1h～13h。通过控制其中两个因素不变，改变其中一个因素，测量机床的定位误差，通过数据统计计算，得到每个因素变化范围内响应输出反向间隙和螺距累积误差的极差值，如表2所示。

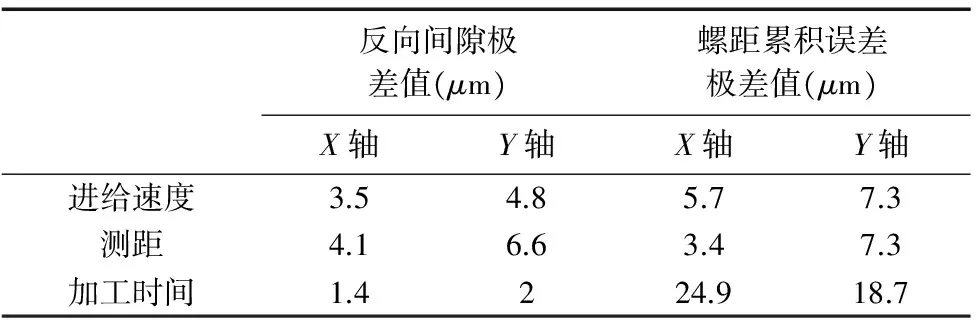
表2 不同因素响应结果极差值

通过表2，可以很明显地对比出，测量时的进给速度和测距相比于加工时间对反向间隙的影响更大，而加工时间则相对于进给速度和测距对螺距累积误差的影响更大。为了更加直观的了解进给速度和测距对反向间隙的影响趋势，以及加工时间对螺距累积误差的影响趋势，作了如图4～图7所示的趋势变化图(其中图5中横轴的点1～6分别表示测距为1mm、5mm、10mm、20mm、50mm、100mm)。

图4 反向间隙随进给速度变化图

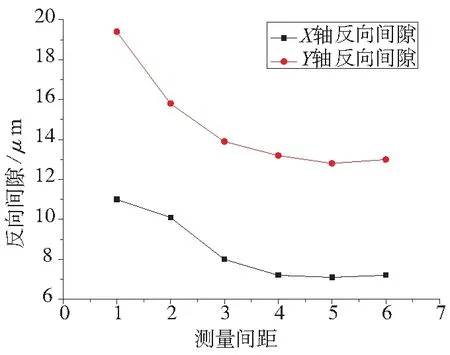
图5 反向间隙随测距变化图

图6 X轴螺距累积误差随加工时间变化图

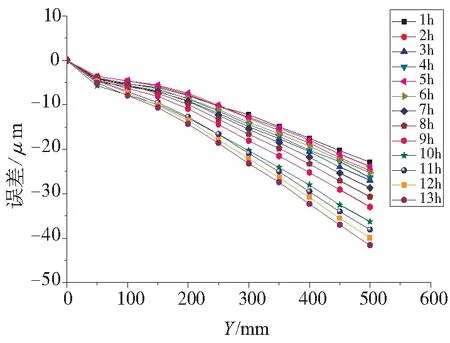
图7 Y轴螺距累积误差随加工时间变化图

由图4可以看出，反向间隙随着进给速度的增大会逐渐减小，到2000mm/min以后变化波动较小。取Y轴800mm/min、1200mm/min、1800mm/min的进给速度进行验证，分别得到Y轴反向间隙为13.6μm、12.9μm、12.7μm，验证成立。由图5可知，反向间隙随着测距的增加而逐渐减小，在测距增大为20mm以后，反向间隙变化波动较小。测距反映的是机床运动的连续性。取Y轴测距为25mm进行验证，得到Y轴反向间隙为12.9μm，验证成立。由图6、图7可知，数控铣床X轴、Y轴的螺距累积误差随着加工时间的增加逐渐增大，这是由于随着机床加工时间的增加，温度逐渐上升，导致机床传动部件发生线性膨胀对定位误差的影响。所以，在编写程序进行工件加工时，要选用合适的进给速度，尽量保证加工的连续性，而且要及时给机床散热。

4 定位误差分布情况分析

4.1 反向间隙可靠度分析

由于机床在制造和装配中存在公差等因素，机床的定位误差也会出现随机性，对机床定位误差的可靠度分析可以判断机床的运动精度保持性以及预测可能出现的误差。在一天时间内，对机床定位误差进行测量，每次测量都是单独的，即每次都是在同一条件下测量。记录100次随机测量结果作为机床反向间隙在某时间段内的总体，可以得到，X轴、Y轴反向间隙的区间分别是(7.4～10.1)μm、(10.5～13.9)μm。将以上区间以0.2μm为间隔，统计落在各个区间里的频数和频率，画出柱状图，再进行高斯拟合，得到如图8、图9所示。

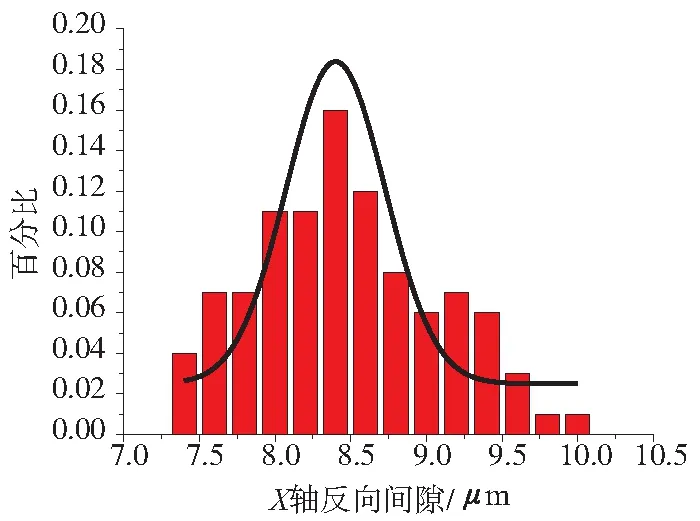
图8 X轴反向间隙统计图

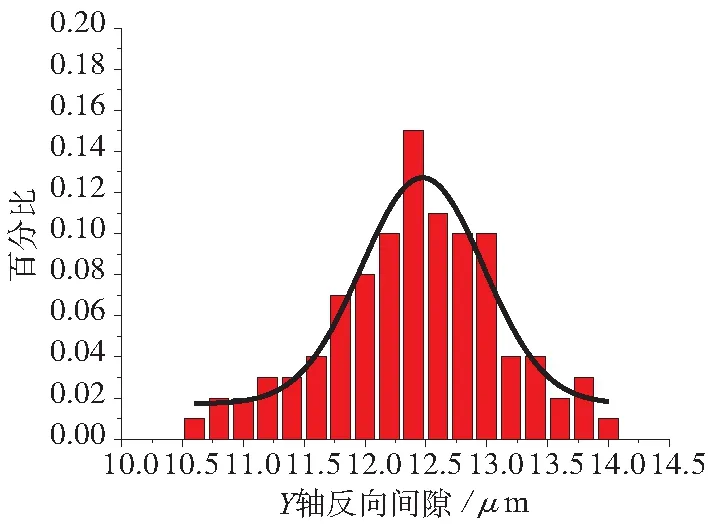
图9 Y轴反向间隙统计图

用N(μ，σ2)表示随机变量θ服从一个数学期望为μ，方差为σ2的正态分布。由图8、图9可知，X轴反向间隙基本服从Nx(8.4，0.4265)的正态分布，Y轴反向间隙基本服从NY(12.4717，1.004)的正态分布。可以得出，X轴相对于Y轴反向间隙较小且更加稳定，Y轴传动机构出现磨损更加严重。

为了检验上述正态分布的可靠度，在同样的条件下，随机选取10次X轴、Y轴反向间隙测量结果，计算出各自的平均值和方差，得到如表3所示。

表3 X、Y轴随机10次反向间隙测量平均值与方差

用随机抽取的小样本数据的数学期望与总体数据的数学期望的偏差大小作为检验机床误差分布情况可靠度的标准，计算得到，X轴反向间隙正态分布可靠度为98.58%，Y轴反向间隙正态分布可靠度为99.05%，可靠度都比较高，可以通过小样本分析目前机床的状况，更加简单准确。

4.2 直线定位精度检验分析

在同一条件下，随机选取50次定位误差测量结果，以100mm为间距，作出各定位点的误差分布曲线，得到如图10、图11所示X轴、Y轴螺距误差各定位点的分布曲线图。(为了观察更清晰，将分布曲线图放大了5倍放入整体的螺距误差变化图里面)

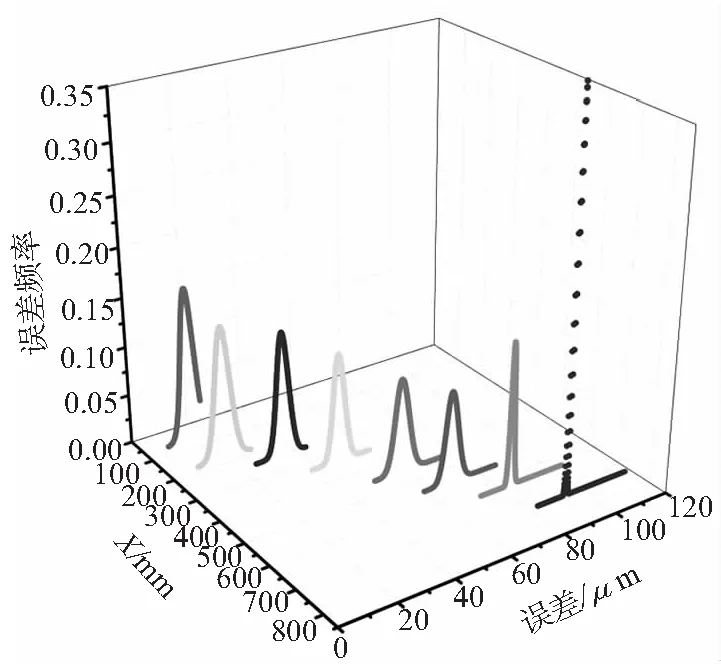
图10 X轴螺距误差各定位点分布曲线图

通过图10、图11可以很直观的得到X轴、Y轴螺距误差的整体变化趋势，并通过分析各测量点的误差分布，可以找出影响定位精度的原因，对误差产生较大的位置，有利于针对性进行误差补偿。从X轴、Y轴的螺距误差分布曲线图可知，X轴各测量点的误差分布相对比较集中，而且随着进给行程的增加，螺距累积误差并没有出现大范围变化，说明测量的X轴螺距误差可靠度比较高，X轴各传动机构状况相对良好，精度保持性较高。而Y轴各误差点分布相对分散，且随着进给行程的增加，螺距累积误差变化范围较大，说明测量的Y轴螺距误差可靠度相对较低，Y轴传动机构磨损较为严重。

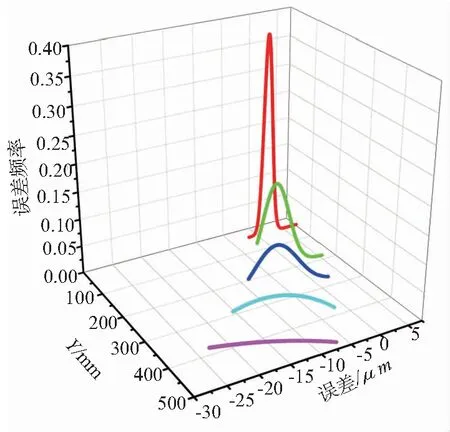
图11 Y轴螺距误差各定位点分布曲线图

5 结论

本文通过对数控铣床定位误差的测量，分析在不同因素影响下的误差测量结果，可以得出以下结论：

(1)外界温度、湿度以及大气压力对机床定位误差的测量有影响，且温度影响最大，其次是大气压，湿度影响最小，可以忽略。

(2)进给速度和测距对反向间隙影响较大，而加工时间则对螺距累积误差影响更大。反向间隙随着进给速度的增大而减小，随着测距的增大而减小，螺距累积误差随着加工时间的增加而逐渐增大。

(3)X轴、Y轴反向间隙分别服从Nx(8.4，0.4265)、NY(12.4717，1.004)的正态分布，且可靠度分别为98.58%、99.05%，可靠度较高。

(4)Y轴相对X轴误差检测的可靠度较低，螺距误差稳定性较差，说明Y轴磨损更加严重，影响加工产品的质量和精度稳定性。

[参考文献]

[1] 庾辉, 李梦奇, 李冬英,等. 数控机床定位精度研究进展[J]. 机械设计与研究, 2015(6):101-104.

[2] Usop Z, Sarhan A A D, Mardi N A, et al. Measuring of positioning, circularity and static errors of a CNC Vertical Machining Centre for validating the machining accuracy[J]. Measurement, 2015, 61:39-50.

[3] Cai L, Zhang Z, Cheng Q, et al. A geometric accuracy design method of multi-axis NC machine tool for improving machining accuracy reliability[J]. Eksploatacja i Niezawodnosc - Maintenance and Reliability, 2015, 17(1):143-155.

[4] Jiang X, Cripps R J. Geometric characterisation and simulation of position independent geometric errors of five-axis machine tools using a double ball bar[J]. International Journal of Advanced Manufacturing Technology, 2016, 83(9-12): 1905-1915.

[5] Kwintarini W, Wibowo A, Martawirya Y Y. Mathematical Approach for Geometric Error Modeling of Three Axis CNC Vertical Milling Machine[J]. Applied Mechanics & Materials, 2016, 842:303-310.

[6] Yang J, Altintas Y. A generalized on-line estimation and control of five-axis contouring errors of CNC machine tools[J]. International Journal of Machine Tools & Manufacture, 2015, 88:9-23.

[7] Chen J Y. Accuracy Measurement and Error Compensation of Three-Axis CNC Milling Machine[J]. Applied Mechanics & Materials, 2014, 651-653:616-619.

[8] Wang W, Zhang Y, Yang J, et al. Geometric and thermal error compensation for CNC milling machines based on Newton interpolation method[J]. Proceedings of Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2013, 227(4):771-778.

[9] Chen T C, Chang C J, Hung J P, et al. Real-Time Compensation for Thermal Errors of the Milling Machine[J]. Applied Sciences, 2016, 6(4):101.

[10] 陈芳. 结合3D测头和宏程序实现机床定位精度自动测量[J]. 组合机床与自动化加工技术, 2016(10):124-127.

[11] 季林, 侯茂盛, 邱丽荣,等. 基于双频激光干涉反馈的快速精密定位系统[J]. 光学技术, 2015, 41(2):156-161.

[12] 高俊翔, 汤善治, 李明,等. 数控机床圆检验测量技术及应用[J]. 电子测量与仪器学报, 2016, 30(12):1805-1811.

[13] 王新孟, 杨军, 梅雪松,等. 精密坐标镗床进给系统热误差分析与预测[J]. 西安交通大学学报, 2015, 49(10):22-28.

[14] 池峰, 朱煜, 张志平,等. 双频激光干涉测量中的环境补偿技术[J]. 中国激光, 2014,41(4):182-188.