Remarks on ‘A new non-specificity measure in evidence theory based on belief intervals”

Joaquı´n ABELLA´N

Department of Computer Science and Artificial Intelligence,University of Granada,Granada 18071,Spain

1.Introduction

Normally,information is expressed via a degree of imprecision.To express our knowledge,we usually use a range of possible values.For example,to express our knowledge in a numerical way,we give a value of belief ‘betweenaandb”(a≤b)for a determinate event.There exist many mathematical models to represent and manipulate information expressed in that way.Usually those models are based on imprecise probabilities(see Walley 1).

One of the most used models based on imprecise probabilities is the Theory of Evidence(TE),also known as Dempster-Shafer’s theory,2,3which was presented as an extension of the classical Probability Theory(PT).In the TE,available information is expressed via a concept called basic belief assignment(bba)on a universe called frame of discernment,which is similar to a probability distribution in the PT.This theory has been widely used in many areas.Some of the most recent and different applications can be seen in Refs.4–13

Many works have been presented in the 90s analyzing uncertainty-based information that a bba can represent.14In the TE,more types of uncertainty have been found than those in the PT.Hence,Yager15makes the distinction between two types of uncertainty,which are called discord(randomness or con flict)and non-specificity,respectively.The first one is related with the entropy and the second one with the imprecision.

Shannon’s entropy16in the PT verifies an important set of desirable properties.A similar set of properties was established in the TE for a measure of uncertainty.17,14To quantify the non-specificity part,only the generalized Hartley measure18verifies an important set of properties.In recent years,other attempts to measure uncertainty in the TE,in a whole way(quantifying both discord and non-specificity)or separately,have appeared.19–23Due to the importance of these measures to be used in applications,their possible drawbacks must be found.24,25That is the principal motivation of the presented paper.

The non-specificity part of uncertainty is associated with cases where information is focused on sets with cardinality greater than one.Then,the non-specificity measures are based on the way to quantify the imprecision in a bba.This type of uncertainty does not appear in the PT,and it can be considered as the principal difference between the PT and other theories that generalize it.The majority of these theories are based on imprecise probabilities.1,26

In the TE,con flict uncertainty appears when focal sets(elements with a positive value of bba)do not share elements,i.e.,they have empty intersections.We can find real situations where there is no con flict and all the uncertainty is a nonspecificity type(see Refs.24,27),when all the focal sets share at least one element and some of them have cardinality over 1.If we find contrary situations,i.e.,uncertainty of only a conflict type,we would be in grounds of the PT and then the classic Shannon’s entropy is the best alternative to use to quantify the uncertainty.Hence,a correct quantification of the nonspecificity uncertainty is important when we choose the TE to represent the information because it is the principal characteristic that distinguishes this theory from the PT.

Very recently,Yang et al.21presented a new measure of non-specificity in the TE.This measure is based on beliefs intervals that a bba represents the single elements of a finite set.The authors simplified the expression of that measure in a function very easy to apply.They showed that this new measure verifies a similar set of properties to those of the generalized Hartley measure:range,monotonicity,symmetry,additivity,and subadditivity.Unfortunately,those two last properties,additivity and subadditivity,are not really verified by the new measure.

The additivity and subadditivity properties are related to the conservation of information.They are coherent properties when we work with different Frames of Discernment(FDs).The first one states that we cannot loss or win information when we combine available information from two different non-interactive(independent)FDs,i.e.,the in formation(uncertainty)that comes from these two sources cannot vary if we want to use them in a combined FD.The subadditivity property states that if we have information on an FD and this FD can be separated on two interactive(dependent)FDs,the original information cannot be increased,i.e.,the uncertainty on the original FD cannot be greater than the sum of the associated uncertainty on each individual FD.

In this paper,we show that the original paper of Yang et al.21has errors in the proofs about the additivity and subadditivity properties.The problems of the mathematical proofs of the authors,about these properties,were that they did not take into account some considerations about the cardinal of the focal sets.Moreover,we use examples to show that the new measure does not really verify those properties.

The paper is organized as follows.Section 2 reviews briefly the necessary background about the TE,uncertainty measures,and the definitions of the properties treated here.Section 3 is devoted to study the additivity and subadditivity of the measure based on belief intervals.Section 4 is dedicated to conclusions.

2.Brief background

2.1.Theory of evidence

The TE2,3is a type of mathematical theory based on imprecise probabilities(see Walley1).Its principal characteristics and principal concepts can be described as follows.

LetXbe a finite set(also called frame of discernment in the TE),considered as a set of possible situations,|X|=n,℘(X)the power set ofX,andxany element inX.The TE is based on the concept of basic belief assignment(bba),also called mass assignment.A bba is a mappingm:℘(X)→ [0,1],so that∑A setAso thatm(A)＞0 is called a focal element(The focal elements can be noted asA∈℘(X)orA⊆X,withm(A)＞0.An empty set is never considered here because alwaysm（∅）=0 ofm).

LetXandYbe finite sets.Consider the product space of possible situationsX×Yand m a bba onX×Y.The marginal bba onX,m↓X(and similarly onY,m↓Y),is defined as follows(the expressions of the marginal bba’s from Eq.(21)in the paper of Yang et al.21have an erratum:The set ‘R’must be‘S’.):

whereRXis the set projection ofRonX.

There are two functions associated with each basic probability assignment,a belief function,Bel,and a plausibility function,Pl:

They can be seen as the belief bounds ofA(lower and upper beliefs of setA,respectively).

We may note that belief and plausibility are interrelated for allA∈ ℘（X）,by Bel（A）=1-Pl（AC）,whereACdenotes the set complement ofA.Furthermore,Bel（A）≤ Pl（A）.Hence,the interval[Bel(A),Pl(A)]is called the belief interval for setA.

2.2.Measures of uncertainty in DST

Shannon 16 presented a measure of entropy on the probability theory defined as follows:

wherepis a probability distribution onX,a finite set,andp(x)is the probability of valuex.Here,log2is normally used to measure the value in bits.S(p)measures the only type of uncertainty presented in the probability theory,and it verifies a large set of desirable properties.7,16

There exist two types of uncertainty in the evidence theory15: ‘one associated with cases where the information is focused on sets with empty intersections;and one associated with cases where the information is focused on sets with cardinality greater than one”.The first concept is known as discord(also as randomness or conflict),and the second one is known as non-specificity.

In the 90s,there were many attempts to quantify the degree of discord in the evidence theory.14However,because of the aims of the paper,we will focus on non-specificity.

The most known measures of non-specificity are the one of Yager15and the one of Dubois and Prade18.

The measure of specificity of Yager15has the following expression:

It was presented to quantify the degree of lack of imprecision,i.e.,the non-specificity degree can be calculated as 1-S(m).Unfortunately,it does not verify all the required properties for such a measure.17

Dubois and Prade18introduced the following function based on the Hartley measure,28that was defined in the classical set theory.It represents a measure of non-specificity associated with a bba,which is expressed as follows:

I(m)attains its minimum value(zero)whenmis a probability distribution.Its maximum value(log2(|X|))is obtained for a bba,m,withm(X)=1 andm(A)=0,∀A⊂X.In the literature,we can check thatIis the only measure of nonspecificity that verifies all the required properties for such a type of measure.

2.3.Additivity and subadditivity of non-specificity measures in the TE

The additivity and subadditivity properties for a Measure of Uncertainty(MU)can be defined as follows24:

Additivity.‘Letmbe a bba on the spaceX×Yandm↓Xandm↓Yits marginal bbas onXandYrespectively so that these marginal bbas are not interactive(m（A×B）=m↓X（A）m↓Y（B）,withA⊆X，B⊆Y;m(C)=0 ifC≠A×B).Then an MU verifies the additivity property iff it satis fies the following equality:

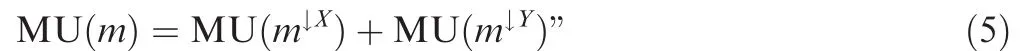
Subadditivity.‘Letmbe a bba on the spaceX×Yandm↓Xandm↓Yits marginal bbas onXandYrespectively.Then an MU verifies the subadditivity property iff it satis fies the following inequality:

They represent important properties that a measure of nonspecificity must verify in the TE.17

3.A measure of non-specificity based on belief intervals

Very recently,Yang et al.21presented a non-specificity measure in the TE based on belief intervals.This measure takes into account the maximum difference between the beliefs of each possible state of a finite setX.If we consider a bbamon a finite setXwith states{x1,x2,...,xn},the new measure is defined using the values Pl({xi})-Bel({xi}),i∈{1,2,...,n}.

The new measure is the average of those values about the belief intervals,and can be expressed as follows:

Its definition has a coherent sense in the way of the definition of the non-specificity concept.This concept is focused on the degree of imprecision of a bba.Then,it is related to the values of the belief intervals used in the definition of the new measure.

The authors have shown that NEBIcan be reduced(The expressions of the summations from Eq.(15)in the paper of Yang et al.21are somehow confusing.For example,to express the value of Pl({θi}),they usedfor Pl({θn}),we could interpret that the summation does not include any term,becausethereisnoj＞n.Itshould beexpressed aswhich represents the correct value in a less confusing way)to the following expression:

3.1.Properties

In the paper of Yang et al.21,it has been proven that the new measure verifies the properties of range,monotonicity,and symmetry that are not discussed here.However,it is also shown that it verifies the multiplicativity and submultiplicativity properties that are equivalent to the additivity and subadditivity properties(they are their counter-part measures17)These properties can be described in a similar way to that for the additivity and subadditivity properties.

Multiplicativity.‘Letmbe a bba on the spaceX×Yandm↓Xandm↓Yits marginal bbas onXandYrespectively so that these marginalbbas are notinteractive (m（A×B）=m↓X（A）m↓Y（B）,withA⊆X，B⊆Y;m(C)=0 ifC≠A×B).Then NEBIverifies the multiplicativity property iff it satis fies the following equality:

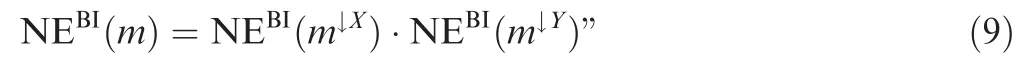
Submultiplicativity.(In the paper of Yang et al.21,the expression about this property is not correct.We have a bbamonX× Y and wetryto provethatNEBI（m）≤NEBI（m↓X）·NEBI（m↓Y),using the marginal bbas.It is not correct to use NEBI（m↓X×m↓Y）,because it is possible thatm≠m↓X×m↓Y.For example,taking the values of the bbamin Example 2,we get that the bbam′=m↓X×m↓Yhas the valuesm′({z21,z22,z31,z32})=0.4 andm′(X×Y)=0.6,that are different from those ofm.)

‘Letmbe a bba on the spaceX×Yandm↓Xandm↓Yits marginal bbas onXandYrespectively.Then a MU verifies the submultiplicativity property iff it satisfies the following inequality:

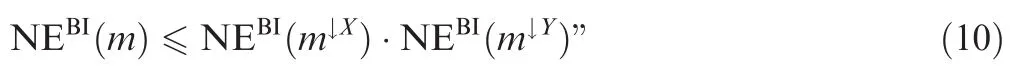
At this point,we want to remark the words in the paper of Yang et al.21about the importance of these properties:‘Note that the physical meaning of submultiplicativity is in essential the conservation of information,i.e.,the amount of uncer-tainty in a joint bba is no greater than the total amount of uncertainty of its corresponding marginal bbas.The equation holds if and only if the corresponding marginal bbas are independent,i.e.,there is not correlated part.”

Now,we consider the following example.

Example 1.With the above notation,letX×Ybe the product space of setsX={x1,x2,x3}andY={y1,y2},andm1andm2the following bbas onXandY,respectively:

Hence,we can build the following bbam=m1×m2onX×Y,and consequently the marginal bbas are not interactive.Thenmhas the following masses:

wherezij=(xi,yj).

The values of uncertainty via the NEBImeasure are

Then NEBI(m)≠NEBI(m1)˙s NEBI(m2),and the multiplicativity property is not satis fied by NEBI.

The above Example 1 serves to us to prove that NEBIalso does not verify the submultiplicativity property.We only need to consider the same bbamonX×Yand then its marginal bbas arem1andm2onXandY,respectively,in that example.We have

which implies that the submultiplicativity property is not verified for NEBI.

From the above results,the new measure does not verify the multiplicativity and submultiplicativity properties,but we find in the paper of Yang et al.21that the authors proved that this measure does verify both properties.We think that the principal error in their proofs is related to the cardinal of the sets.For example,ifA⊆XandB⊆Y, thenA×B⊆X×Yand it is possible to find the focal sets of each bba so that|A×B|＞1 and|A|=1,|B|＞1,as happen in Example 1.

To analyze the proof about multiplicativity,we apply the values of Example 1 on the penultimate step in Eq.(23)in the paper of Yang et al.21.We can see the following situation,detailing the calculus(To simplify,setsAare in space X,and setsBin spaceY)from Example 1:

It is easy to see that

Hence,the penultimate step in Eq.(23)in the paper of Yang et al.21is not correct.

As we see,focal elements with cardinal 1 in setX,i.e.,sets that do not produce any imprecision,can be components of sets in the product spaceX×Ythat produce imprecision.This has not been considered in the proof of the multiplicativity in the paper of Yang et al.21.

Now,we analyze the proof of the submultiplicativity property and find that the last step cannot be correct in some situations.That last step expresses the following equality(moreover,in Ref.21,the expression NEBI（m↓X×m↓Y）should be NEBI（m），using the correct definition of the property26):

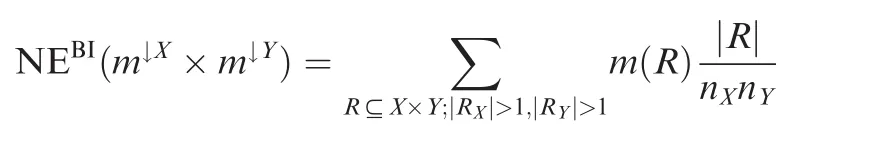
However,this equality is not always correct.Again,if we consider the values of Example 1,the left term of the above equality is NEBI(m)and contains the following addend:

Now,consideringR={z31,z32},we have thatRX={x3}and|RX|=1.Hence,that addend cannot be in the right part of the equality.We conclude that the equality is not correct in this case.

We could think that this measure could be supermultiplicative,i.e.,with the above notation,it always verifies that

but with the following example,we see that it is also not so.

Example 2.LetX×Ybe the product space of setsX={x1,x2,x3}andY={y1,y2},andmthe following bba onX×Y:

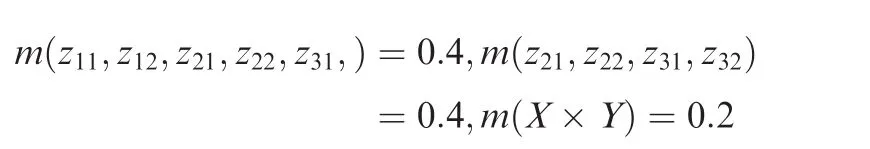
wherezij=(xi,yj).

Now,the marginal bbas onXandYhave the following values:

The values of uncertainty via the NEBImeasure are

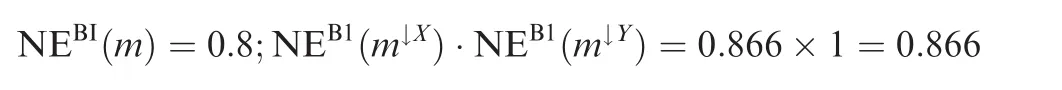
Hence,NEBI（m）＜ NEBI（m↓X）·NEBI（m↓Y）,and the supermultiplicativity property is not satis fied by NEBI.

Examples 1 and 2 represent a very con flictive situation for this new measure.If we have a complex problem in the TE and we can reduce the complexity using projections on 2 less complex sets,via the marginal bbas,we see that in some situations,the information(uncertainty)available can be decreased,while in other situations,it can be increased.This is a very bad behavior for this measure.

4.Conclusions

(1)In this paper,we have analyzed the properties of additivity and subadditivity of a new measure of nonspecificity.We have detected some errors in the original proofs presented to show that the measure verifies such properties.It has also been shown that the measure presents incoherent results when a decomposition is done using the same functional projections:in some situations,that decomposition presents an increase in information,butin others,itpresentsa decreaseof information.These results must be known.In addition,we have detected some other misprints and inaccuracies in the original paper where the new measure was presented.

(2)Here,we do not discuss the possible utility that could have that measure,but with the results presented here,the use of this measure could not be appropriate in some situations,decreasing its importance to be used in applications.

(3)In the original paper where the measure has been presented,21we can find applications where the measure can give coherent results(Examples 1–4).In those applications,the concepts of interactive or non-interactive frames of discernment are not used.Hence,a use of belief intervals can be useful in some situations,but the definition of a total coherent measure based on this tool is still an open question.As we mentioned in the paper,belief intervals are related to the value of nonspecificity of a bba,but the problem is the way to use them.

(4)So far,the generalized Hartley measure and the ones presented in Ref.27are the only measures that have a theoretical coherent behavior under our point of view.These measures could serve the aims of the paper that we have analyzed here.It will be a matter of our future work,where we also try to find utility to the use of belief intervals for this type of measures.

Acknowledgements

We would like to thank E.Bosséfor his help in drawing up this work.This work was supported by the Spanish ‘Ministerio de Economı´a y Competitividad” and by ‘Fondo Europeo de Desarrollo Regional”(FEDER)(No.TEC2015-69496-R).

1.Walley P.Statistical reasoning with imprecise probabilities.New York:Chapman and Hall;1991.

2.Dempster AP.Upper and lower probabilities induced by a multivaluated mapping.Ann Math Stat 1967;38(2):325–39.

3.Shafer G.A mathematical theory of evidence.Princeton:Princeton University Press;1976.

4.Liu Z,Pan Q,Dezert J,Mercier G.Credal classification rule for uncertain data based on belief functions.Pattern Recogn 2014;47(4):2532–41.

5.Su X,Mahadevan S,Xu P,Deng Y.Dependence assessment in human reliability analysis using evidence theory and AHP.Risk Anal 2015;35(7):1296–316.

6.Tang J,Wu Z,Yang C.Epistemic uncertainty quantification in utter analysis using evidence theory.Chin J Aeronaut 2015;28(1):164–71.

7.Li D,Wang H,Wang R,Xiong Y.Professional competence evaluation of information management undergraduates based on rough set and DS evidence theory.Int J Database Theory Appl 2016;9(5):111–20.

8.Yang K,Liu S,Li X,Wang XA.DS evidence theory based trust detection scheme in wireless sensor networks.Int J Technol Human Interact 2016;12(2):48–59.

9.Han D,Liu W,Dezert J,Yang Y.A novel approach to preextracting support vectors based on the theory of belief functions.Knowl-Based Syst 2016;110:210–23.

10.Wang Q,Li W,Wu Y,Pei Y,Xing M,Yang D.A comparative study on the landslide susceptibility mapping using evidential belief function and weights of evidence models.J Earth Syst Sci 2016;125(3):645–62.

11.Farah MB,Mercier D,Delmotte F,Lefevre E.Methods using belief functions to manage imperfect information concerning events on the road in VANETs.Transport Res Part C:Emerg Technol 2016;67:299–320.

12.Denoeux T,Sriboonchitta S,Kanjanatarakul O.Evidential clustering of large dissimilarity data.Knowl-Based Syst 2016;106(15):179–95.

13.Liu Z,Pan Q,Dezert J,Mercier G.Hybrid classification system for uncertain data.IEEE Trans Syst Man Cybern:Syst 2016;PP(99):1–8.

14.Klir GJ,Wierman MJ.Uncertainty-based information.Berlin:Phisica-Verlag HD;1998.

15.Yager RR.Entropy and specificity in a mathematical theory of evidence.Int J Gen Syst 1983;219(4):291–310.

16.Shannon CE.A mathematical theory of communication.Bell Syst Tech J 1948;27(4):379–423.

17.Dubois D,Prade H.Properties of measures of information in evidenceand possibility theories.FuzzySetsSyst1987;24(2):161–82.

18.Dubois D,Prade H.A note on measure of specificity for fuzzy sets.Int J Gen Syst 2007;10(4):279–83.

19.Shahpari A,Seyedin SA.Using mutual aggregate uncertainty measures in a threat assessment problem constructed by Dempster-Shafer network.IEEE Trans Syst Man Cybern:Syst 2015;45(6):877–86.

20.Deng Y.Deng entropy.Chaos Solut Fract 2016;91:549–53.

21.Yang Y,Han DQ,Dezert J.A new non-specificity measure in evidence theory based on belief intervals.Chin J Aeronaut 2016;29(3):704–13.

22.Yang Y,Han DQ.A new distance-based total uncertainty measure in the theory of belief functions. Knowl-Based Syst 2016;94:114–23.

23.Wang J,Hu Y,Xiao F,Deng X,Deng Y.A novel method to use fuzzy soft sets in decision making based on ambiguity measure and Dempster-Shafer theory of evidence:an application in medical diagnosis.Artif Intell Med 2016;69:1–11.

24.Abella´n J,BosséE.Drawbacks of uncertainty measures based on the pignistic transformation.IEEE Trans Syst Man Cybern:Syst 2016;PP(9):1–7.

25.Abella´n J.Analyzing properties of Deng entropy in the theory of evidence.Chaos Solut Fract 2017;95:195–9.

26.Klir GJ.Uncertainty and information:foundations of generalized in formation theory.Hoboken,NJ:John Wiley;2016.

27.Abella´n J.Combining non-specificity measures in Dempster-Shafer theory of evidence.Int J Gen Syst 2011;40(6):611–22.

28.Hartley RVL.Transmission of information.Bell Syst Tech J 1928;7:535–63.