Experimental research in rotating wedge-shaped cooling channel with multiple non-equant holes lateral inlet
2018-04-19HuiminZHOUHaiwangLIZhiTAOHongwuDENGMeisongYANGShuqingTIAN
Huimin ZHOU,Haiwang LI,Zhi TAO,Hongwu DENG,*,Meisong YANG,Shuqing TIAN
aNational Key Laboratory of Science and Technology on Aero-Engine Aero-Thermodynamics,Beihang University,Beijing 100083,China
bCollaborative Innovation Center of Advanced Aero-Engine,Beihang University,Beijing 100083,China
cResearch and Development Center,AVIC Commercial Aircraft Engine Co.,Ltd.,Shanghai 201108,China
1.Introduction
Demands of higher efficiency of modern advanced gas turbines require them operate in a temperature higher than the melting point of the blade,to promote the development of both internal and external cooling techniques to enhance turbine heat transfer.Previous experimental studies on internal cooling technology of advanced gas turbines have been summarized by Han and Huh1–3Internal cooling approaches vary with different parts of the turbine to respond to different needs and achieve the best cooling effect.The trailing edge is one of the most challenging regions due to typically narrow cooling channels.The structural features of the turbine trailing edge can be summarized asfollows:wedge-shaped converging crosssection,pin- fin or other turbulence promoters,lateral coolant ejection and large installation angle.Coriolis force and buoyancy force generated in a rotating state make the flow and heat transfer inside the channel further complicated.
Under static condition,many studies have been done and confirmed that the flow and heat transfer of turbine trailing edge are mainly influenced by pin- fin cooling configuration and cooling channel structure.Lateral ejection is one of the most effective characteristics.Lau et al.4,5studied a pin- fin cooling channels with lateral ejection structure.The results showed that the decreasing rate of mass flow along the channel caused by the lateral ejection reduced the downstream heat transfer of the channel and furt6her affected the overall heat transfer.Wright and Gohardanifound that the heat transfer of both rectangular channel and wedge-shaped channel is uniform in the cross-section without lateral ejection,and the lateral ejection structure is very effective in increasing the heat transfer coefficient near the out flow holes.Kumaran et al.7confirmed Lau’s conclusion and found that the length of ejection holes had little effect on the channel heat transfer by comparing the heat transfer three different channel configurations pin- fin roughened channel with short lateral ejection holes,with long ones and without lateral ejection holes.McMillin and Lau8studied a pin- fin arrayed rectangular channel with naphthalene sublimation technique and drew the conclusion that the turning of main flow caused by side-wall ejection generated higher mass transfer near the ejection but lower near the opposite inner region.Taslim et al.9studies a wedge-shaped channel with lateral ejection and observed a significant span-wise heat transfer difference due to the trapezoidal converging configuration.It was also found that this span-wise heat transfer variation can be apparently weakened by the side-wall ejection.Hwang et al.10conducted experiments involving eight wedge-shaped channels with different pin- fin and outlet configurations to study the effect of lateral-to-total flow ratio.It was found that the heat transfer was the worst when the ratio approached to 0.3.Hwang and Lu11confirmed that the effect of lateral-tototal was a main factor as well as pin shape after further study via transient liquid crystal technique.The worst heat transfer happened when the ratio approached 0.3–0.4 depending on different pin shape.Kan et al.12did numerical simulation of flow and heat transfer in a high aspect ratio channel with lateral ejection.It was shown that the heat transfer near the end of channel reduced due to a significant flow separation happened there.
Rotating experimental researches are more challenging than the static ones.Chang et al.13found that the heat transfer in a rib roughened wedge-shaped channel with side-wall ejection holes was lower than that without the side-wall ejection ones,especially in a rotating state.However,the experiments were conducted when the installation angle of channel was 90°rather than the real configuration of a trailing edge cooling channel.Wright et al.14studied the heat transfer characteristics of a rotating smooth wedge-shaped cooling channel with radial out flow under the channel configuration of 135°.The experimental results showed that the rotation number and buoyancy number are ideal parameters for describing the rotational heat transfer characteristics of the channel.The effect of rotation on the leading surface was greater than that on the trailing surface.There was a critical rotation leading to the obvious change of the heat transfer on the leading surface.Liu et al.15did similar investigation but the experiment channel was with lateral ejection.It was found that the lateral ejection weakened the rotation effects and enhanced the overall heat transfer inside the channel for inducing turbulence mixing.The local heat transfer near the out flow slots was especially increased due to a gas film formed near the ejection.Rallabandi et al.16added pin- fins inside the channel which enhanced the heat transfer and weakened the effect of rotation.Liu et al.17also did experiments with turbulators and obtained similar conclusions.Qiu18and Tao19et al.experimentally investigated the effects of channel orientation,outlet boundary condition on flow and heat transfer in a rotating wedge-shaped channel with lateral fluid extraction.The results indicated that the channel orientation was an in fluential factor on channel heat transfer,thus should be chosen carefully to simulate the actual conditions of the turbine.The heat transfer of the channel’s inner top region approached the worst point and was sensitive to the rotation effect under the channel configuration of 90°.Srinivasan et al.20examined Qiu’s experiments18by numerical simulation and confirmed that the heat transfer on the trailing wall was enhanced significantly by rotation.Pardeshi et al.21numerically investigated more complex situation additionally considering pin- fin/rib turbulators.Li et al.22added an additional inlet to wedge-shaped channel at the inner top region and experimental investigated the flow and heat transfer under both rotating and non-rotating conditions.As a result,the second inlet notably improved the heat transfer at the top of the channel and compensated the negative effects induced by the rotation.When the mass flow rate ratio(second inlet mass flow rate/major inlet mass flow rate)came to 0.3,the second inlet benefited overall heat transfer at high rotation numbers.
From the foregoing,previous studies have confirmed that both lateral outlets and inlets have positive effect on heat transfer of the channel and can weaken the impact of rotation.However,adding a second coolant inlet at the top of the channel can only improve the local heat transfer in the vicinity of the inlet but does not benefit the overall heat transfer enough.From the overall perspective,the negative effect of rotation can lead to local overheating of the channel and low efficiency of coolant utilization.The objective of this paper is to further improve the overall heat transfer of turbine trailing edge cooling channel and decrease adverse impact of rotating.Concretely,the second inlet is expanded from one single hole to multiple lateral holes.The radius of those holes varies depending on their location to enhance channel heat transfer uniformity and improve the utilization efficiency of the cooling air by controlling the mass flow rate through different holes.Experiments have been done to research the effect of this new inlet structure under both static and rotating states and the results are summarized.
2.Experiment setup
2.1.Rotating facilities
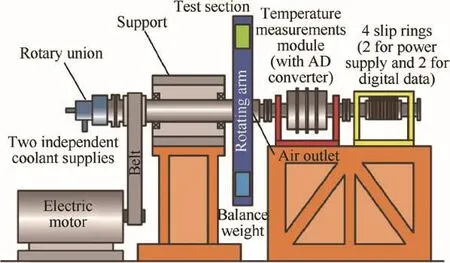
Fig.1 Rotating facility.
As shown in Fig.1,the rotating facility consists of four main modules connected by standard interface,which are electric motor,airing system,rotating arm with support and measurements module.Before being supplied into the rotating facility through a Deublin rotary union,two passes of cooling air cooling air individually pass through a FCI-ST98 thermal flow meter and a GEMU electromagnetic valve.The FCIST98 thermal flow meter can collect the mass flow rate in real time,the measuring range of which is from 0 to 29.5 kg/h and from 0 to 60 kg/h.The GEMU electromagnetic valve cooperating with thermal flow meter achieves automatic control of mass flow rate by regulating valve opening according to the difference between the real-time mass flow rate and set value.The test section is placed at the top of the rotating arm with the maximum rotating diameter of 1.3 m.Cooling air through test section is directly discharged to the atmosphere.In order to ensure a large enough range of the rotation number,a throttle valve is set at the exit of the channel so that the pressure inside the channel is maintained at about 5 times the atmospheric pressure.Temperature measurement is accomplished by thermocouples.The cold ends of the thermocouples are placed in a rotating cavity isolated from hot parts to ensure that the temperature in this cavity could be considered as constant and uniform.The analog signals are converted into digital ones before being transmitted to the non-rotating facilities by slip rings.More details about the rotating facilities can be found in our previous works.22–24
2.2.Test section
The test channel is simplified and amplified by five times on the base of actual cooling channel.The dimensions of test model are shown in Fig.2.The channel consists of 230 mm long heated section and a 63 mm long unheated entrance region.The cross-section of the heated channel is a trapezoid with a height of 57.5 mm.The 20 mm wide edge of this wedge narrows to 6 mm and gives the apex an angle of 15.Thus,the Area of the cross section(A)is about 702 mm2and the hydraulic diameter(Dh)is 22.9 mm.The height of the bottom inlet is 2/3 of the heated channel,thus there is a sudden expansion of the entrance,which is similar with actual channel.The distance from the axis of rotation to the major inlet of heated section is 350 mm.The second inlet consists of 8 circular holes located on the side-wall whose diameters vary from 6 mm to 12 mm.Eight slots are drilled on the narrow side-wall,through which the coolant is ejected from the heated channel.The pressure inside the channel is maintained at 5×105Pa by manual regulation through a throttle valve.
Forty-eight copper plates with a surface area of 22 mm×16 mm are embedded on Nylon made leading and trailing surfaces.A T-type thermocouple is inserted into the back side blind hole of each copper plate to measure the average surface temperature of the copper.One film heater is glued on the back of copper plate to supply the heat energy.In the span-wise direction of the channel,the channel is divided into three parts(inner,mid-span and outer)according to the location of copper plates.And in the stream-wise direction,there are eight locations numbered from P1to P8.Since the resistances of those heaters that connected in series are basically the same,the overall thermal boundary could be considered as iso- flux.Ω in Fig.2 is the rotating angular velocity of the channel.To simulate the real turbine blade trailing edge configuration,the channel is oriented at 135°respect to the rotating plane.1,18The inlet temperature(Tin)is 292 K.The wall temperature ranges from 315 K to 370 K and the average wall temperature is about 335 K.Other details of working conditions are listed in Table 1.

Fig.2 Dimensions of test channel.

Table 1 Working conditions of test channel.
3.Data reduction
To facilitate the experiment,the mass flow rate of major inlet is confirmed while that of second inlet is adjustable.The Mass flow rate Ratio(MR)is defined as follows based on main inlet to describe the proportion of bottom inletand lateral inlet

or

The total inlet mass flow rate ratio is defined as the ratio of lateral flow to total flow so as to research the role of lateral inlet as follows:

Both entries correspond to a Reynolds number.Reynolds number of working condition is defined with the major inlet mass flow rate for unified comparison as Eqs.(4),(5):

where ρ is the density of the fluid,μ is the viscosity,and Vinis the velocity of the inlet flow.In this paper,Re refers to Remainwithout special instructions.
The effective Reynolds number is defined with total inlet mass flow rates to describe conditions while different inlet is major inlet as Eq.(6):

where Vin,sumis the equivalent velocity of coolant from both inlets.
Rotation number is defined as follows to represent the magnitude of rotation:

where n is the rotational speed.
Nusselt number is defined as follows:

where λ is the thermal conductivity of the coolant,h is heat transfer coefficient.
The regionally averaged heat transfer coefficient depends on the net heat flux of the inner wall of the channel(Qnet),heat transfer surface area,regional average wall temperature(Tw)and the overall average bulk temperature(Tb).And the specific definition is shown in Eq.(9):

The net heat flux can be calculated as Eq.(10)with total electrical energy and the heat loss(Qloss),which can be estimated by heat loss coefficient(α)and the difference between wall temperature and environment temperature(Te):

where I is the electric current,and Riis the resistance of each temperature measuring point.
The heat loss coefficient is a function of angular velocity which varies with the change of dimensionless position and can be calibrated by heat loss experiments as follows:

The local bulk temperature(Tb,x)is difficult to measure or calculate directly because it changes greatly under different operating conditions.So in this experiment,it is described by overall averaged bulk temperature as follows:

where Toutis the temperature at the outlet,and cpis the heat capacity of the coolant.
As coolant from two inlets is at the same temperature,Tbcan be further simplified as follows:

Thermal conductivity is defined as follows:

where λ0is the thermal conductivity of air at standard atmospheric pressure,and the qualitative temperature Tf,xis selected as Tb,xin this paper.
The regional buoyancy number is defined as follow:

in which TR represents the local temperature ratio of the channel and RLrepresents the radius of gyration.The temperature ratio is fixed to 0.14 as the real turbine working conditions on the basis of previous studies.The temperature ratio has an effect on heat transfer characteristics by changing the physical properties and the buoyancy force in the channel.At low rotational speeds,the weakening effect on the heat transfer due to change of the physical property is greater than the enhancement of that due to the increase of buoyancy force.But this effect is not obvious in the actual experimental process as shown in Fig.3,where the ordinate Nu/Nusrepresents the ratio of span-wise average Nusselt number under rotating conditions and that under static conditions.With the increase of the rotation number,the effect of buoyancy increase on heat transfer becomes more and more obvious and the two effects of the temperature ratio cancel each other out.When the rotation number further increases and the influence of buoyancy becomes dominant,especially at the top of the channel,the heat transfer is enhanced with the temperature ratio increasing but the maximum of heat transfer differences between conditions where TR=0.14 and TR=0.08 is less than 8%.So it can be considered that the change of temperature ratio is negligible in this paper.For another,the RL/Dhis a constant in this experiment.So buoyancy number has the same effect as the rotation number in this paper.
The measured Nusselt numbers are customarily compared with Dittus-Boelter/McAdams correlation or data under static conditions to normalize the data as Eq.(16).In this study,the Prandtl number(Pr)is a constant of 0.4.In the following discussion,Nu0is the average Nusselt number of fully developed turbulence in a static smooth pipe with the same hydraulic diameter as the channel,and Nu0is calculated with the effective Reynolds number without special instructions.It has been proved in previous studies that the Nu/Nu0is a good way to normalize the Nusselt number.22


Fig.3 Effect of local temperature ratio on heat transfer in a channel with bottom inlet under rotating conditions(Re=20000,MR=0).
Fanning friction factor(f)is employed as the flow resistance coefficient to describe the frictional losses within the channel.Thus,in Eq.(17),pinand poutrespectively represent static pressure at the inlet and outlet,is the dynamic head at the radial inlet channel cross-section, Δpe,cenis a correction term for pressure changes caused by centrifugal force,and L is the length of the channel.In this experiment,the pressure difference between inlet and outlet is not influenced by centrifugal force because the pressure measuring points are on the same rotating radius.

To comprehensively analyze heat transfer and flow resistance caused by different channel structure and other factors,the thermal performance(η)is described as Eq.(18)based on the constant pumping power condition25:

The resistance coefficient and the thermal performance are normalized in the same way as Nusselt numbers.Nus,ηsand fsare data under static conditions;Nu0,η0and f0are data of fully developed turbulence in a static smooth pipe with the same hydraulic diameter as the channel.

Actually the experiment model and real blade are incompletely similar,which is subject to the rotation radius and rotating speed under laboratory conditions.Two main problems can be caused by incomplete similarity.First,it is difficult to match critical criterion numbers;Second,the small rotation radius can result in a small buoyancy number.As this experiment is conducted at a fixed temperature ratio,the correction of buoyancy number is not discussed in this essay.To match critical criterion numbers,the pressure inside the experiment channel is maintained at about 5 times the atmospheric pressure,which decreases the coolant velocity and increases the coolant density at the inlet.Thus,the rotation number is raised without changing the Reynolds number and similar experimental studies can be carried out.26,27The experimental error is given in Appendix A.
4.Results and discussion
4.1.Non-rotating channel with single inlet

Fig.4 Distribution of Nusselt number ratios at non-rotating conditions with either bottom inlet or lateral inlet(TR=0.14,MR=0,Ro=0).
The Nu/Nu0distributions along the channel with only bottom inlet or lateral inlet is shown in Fig.4.The results show that under non-rotating conditions,the major inlet Reynolds number barely affect the heat transfer distribution curve,which allows easier analysis of the data under different Reynolds number conditions and wider application of the experimental results.The heat transfer difference between the leading and trailing wall is inconspicuous because of geometric symmetry.Under conditions with only bottom inlet,the heat transfer capacity significantly decreases in stream-wise direction.This phenomenon can be attributed to the coolant continuously spilling from lateral ejection,so the cooling air at the top of the channel is much less than that at the bottom of the channel.In span-wise direction,except P1,the heat transfer at the outer region is higher than that at the mid-span and inner area,for the air flow is accelerated when turning nearly 90°and being ejected through side-wall slots.However,at P1,a flow dead zone formed due to the sudden expansion of the entrance as shown in Fig.5,which slightly weakens the heat transfer near the outer surface.As a comparison,lateral inlet apparently improves the heat transfer at high radius area of the channel.In the ideal case,the coolant should be injected in exact span-wise direction and make the heat transfer uniform throughout the whole channel.In the actual experiment,however,the air flow incidence angle is not exact 90°especially in the vicinity of the root of the channel as the cooling air is injected radially initially and sharply turns to the axial direction,which gives rise to a flow dead zone and reduces the heat transfer near the bottom inlet as shown in Fig.6.When the airflow reaches the middle of the channel,the injection direction is gradually close to axial and the impact effect is strengthened,which enhanced the heat transfer around the middle.On the contrary,the heat transfer at the top of the channel slightly decreases.The reason can be inferred that less cooling air is injected from the top holes.In span-wise direction,the midspan region of the channel present better heat transfer characteristics than the outer and inner areas for being directly impinged by the coolant as shown in Fig.6.Compared with conditions with only bottom inlet,the average heat transfer in the channel with lateral inlet is respectively enhanced by 30.01%and 28.87%when the Reynolds number is 10000 and 20000.And the heat transfer at the high-radius half channel(P5–P8)respectively increases by 168.2%and 128.3%with the Reynolds number 10000 and 20000.Partial data at P8are missing due to thermocouple damage but it has little impact on interpretation of the trend of the whole curve.

Fig.5 Flow distribution at non-rotating conditions with bottom inlet.

Fig.6 Flow distribution at non-rotating conditions with lateral inlet.
4.2.Non-rotating channel with two inlets

Fig.7 Distribution of the Nusselt number ratios at non-rotating conditions with two inlets(Re=12000,TR=0.14,Ro=0).
Fig.7 shows the Nu/Nu0distribution in the non-rotating channel with two inlets varying with MR.Reynolds number of the main inlet is kept at 12000 and the MR changes from 0 to 1.0.Considering the good symmetry of the heat transfer on the leading wall and the trailing one,data at corresponding points on both sides are averaged.In Li’s study22,the heat transfer on the top of the channel grows with the ratio of the second coolant injection to total flow.But a decrease in bottom inlet coolant leads to the decrease in Nu/Nu0at the first few locations of the channel.Similarly,in this experiment the lateral inlet expands the influence of the second injection.In short,bottom injection is good for the first few locations while lateral injection benefits the heat transfer from the middle to the top of the channel.It can be inferred that there is a proper MR that is relatively best for the overall heat transfer.
In order to further study the influence of the mass flow rate ratio on the local heat transfer of the channel,48 temperature measurement points were divided into four areas and numbered 1–4.Averaged data of these four areas are organized by the total inlet mass flow rate ratio(MR′)and the result is shown in Fig.8.It is shown that before MR′reaches 0.2,the heat transfer in Area 1 is almost the same,and that in other 3 areas decreases due to the reduction of the proportion of bottom inlet coolant.When MR′exceeds 0.2,the heat transfer in Area 1 decreases while heat transfer in other 3 areas is enhanced by lateral injection.The standard deviations of Nu/Nu0in these 4 areas are organized by MR′and shown in Fig.9.When MR′approaches 0.56,i.e.when the coolant from two inlets is roughly equal,the heat transfer inside the channel is the most uniform.Considering both intensity and uniformity of the heat transfer,it can be concluded that the lateral mass flow rate of about half of the total mass flow rate is the best option under non-rotating conditions.

Fig.9 Effect of mass flow rate ratio on standard deviation of averaged Nusselt number ratios at non-rotating conditions with two inlets(Re=12000,TR=0.14,Ro=0).

Fig.8 Effect of mass flow rate ratio on Nusselt number ratios at non-rotating conditions with two inlets(Re=12000,TR=0.14,Ro=0).
4.3.Rotating channel with single inlet
Figs.10 and 11 present the Nu/Nusdistribution of each measuring point with rotation number at different Reynolds numbers(Re=10000 and Re=20000)in rotating channel with either bottom inlet or lateral inlet.The curves at different Reynolds numbers are quite similar but the rotation effect reduces under higher Reynolds number at the top of the channel with bottom inlet so the curve fluctuation amplitude decreases in Fig.10(b),which may be attributed to the increase of coolant.In the channel with bottom inlet,rotation enhances the heat transfer on the trailing wall and weakens that on the leading wall.This phenomenon is especially obvious in the vicinity of the sudden expansion entrance and the top of the channel.Lateral injection reduces negative effect of rotation to a certain extent.In comparison,Nu/Nusof channel with lateral inlet is almost independent with the rotation number and the heat transfer disparity between two walls is apparently reduced.Two counter-current zones are formed at the top of the channel(P8)and the inner region in low radius area(P2and P3),where the average air flow velocity is from the top of the channel to the bottom and the heat transfer on the leading wall is enhanced.
Fig.12 shows the Nu/Nu0distribution along a rotating channel with lateral inlet at Reynolds number of 10000.Due to the lateral inlet,rotation has hardly affected the distribution except enhancing the heat transfer near P2and P3on the leading wall.The heat transfer on the leading wall and the trailing wall still has a good symmetry and the overall heat transfer is uniform.Similar statement is also applicable to the condition at Reynolds number of 20000(Fig.13).
4.4.Rotating channel with two inlets
For a clearer study of the effect of the mass flow rate ratio on the heat transfer characteristics along the channel,the parameters are averaged along the span direction as follows:

Fig.10 Effect of rotation on Nu/Nusin channel with bottom inlet(TR=0.14,MR=0).

Fig.11 Effect of rotation on Nu/Nusin channel with lateral inlet(TR=0.14,MR=0).

Fig.12 Effect of rotation on distribution of Nusselt number ratios in channel with lateral inlet(TR=0.14,Re=10000,MR=0).

Fig.13 Effect of rotation on distribution of Nusselt number ratios in channel with lateral inlet(TR=0.14,Re=20000,MR=0).

Fig.14 Effect of rotation on distribution of Nusselt number ratios in channel with two inlets(TR=0.14,Re=12000).

where the subscript‘T” is for trailing surface,the subscript‘L”is for leading surface,andthe subscript‘outer”,‘mid” and ‘inner”represent different area of the channel as shown in Fig.2.
It has been discussed that when the total mass flow rate ratio is about 0.5,it is proper for both intensity and uniformity of heat transfer under non-rotating conditions.Experiments have been done to acquire the appropriate MR′considering the effect of rotation and the Nui,ave/Nu0distribution is shown in Fig.14.When MR′is less than 0.5,i.e.coolant from bottom inlet is the main flow,the effect of lateral cooling air on the high radius of the channel is more obvious.When the proportion of lateral coolant is over 50%,lateral air flow’s sphere of influence is expanded to the total channel.When keeping increasing the lateral coolant,heat transfer at the middle and top of the channel is further enhanced with that near the bottom inlet decreasing.
Fig.15 shows the distribution of normalized resistance coefficient and the thermal performance in a two-inlet channel under the rotating condition.With the increase of the lateral injection,the flow resistance in the channel increases firstly and then decreases obviously.The effect of rotation on the parameters is not significant.Comparing with the condition where MR′=0.5,the f/f0decreases by 8.57%and the η/ηsincreases by 5.34%.
Considering the overall heat transfer and flow resistance of the channel,the total mass flow rate ratio of 0.67 is an appropriate option.

Fig.15 Effect of rotation on normalized resistance coefficient and synthesis coefficient in channel with two inlets(TR=0.14,Re=12000).
5.Conclusions
The flow and heat transfer in a smooth wedge-shaped channel with two inlets(bottom inlet and lateral inlet formed by multiple non-equant holes)and lateral coolant ejection is studied.48 temperature measurement points distributed on the inner surface of the channel and other measuring equipment provide the regionally averaged heat transfer coefficients.All the experiments are conducted at the inlet Reynolds numbers from 10000 to 20000 and rotation number from 0 to 1.16.The total mass flow rate ratio(lateral mass flow rate/total mass flow rate)varies from 0 to 1.0.The temperature ratio is fixed to 0.14 as the real working conditions of turbine.Conclusions based on experimental facts can be summarized as follows.
(1)In non-rotating conditions,lateral injection improves the heat transfer at the middle and the top of the channel but reduces at the low-radius areas.With lateral inlet,the average heat transfer in the channel with lateral inlet is respectively enhanced by 30.01%and 28.87%while the heat transferat the high-radius half channel(P5–P8)respectively increases by 168.2%and 128.3%with the Reynolds number 10000 and 20000 compared with conditions with only bottom inlet.
(2)In non-rotating conditions,when the lateral flow rate is about half of the total flow rate,the intensity and uniformity of overall heat transfer is satisfying.
(3)In rotating channel,the negative effects induced by rotation are significantly compensated by lateral injection and the heat transfer disparity on the trailing side and leading side of the channel is reduced to an acceptable range.The heat transfer at the middle and top of the channel is notably enhanced with that at the bottom of the channel reducing.The heat transfer distribution is almost free from the impact of rotation.
(4)Proper proportion of lateral coolant also helps decrease the flow resistance inside the channel.The flow and heat transfer performance is the best when the total flow rate ratio is about 0.67.
Sincere gratitude goes to AVIC Commercial Aircraft Engine Co.,Ltd.for the help in the research process,including providing information and helping confirm experimental project.
Appendix A
The main control variables used in this paper are the Reynolds number and the number of rotations while the main variable is the Nusselt number.The direct measurement quantities in the experiment mainly includes temperature(T),pressure(p),rotating speed,current,mass flow rate(m˙)and geometric dimensions.The direct measurement errors caused by the measurement tools and methods in this experiment are shown in Table A1.In Table A1,M represents the measuring range of flowmeter.
The errors of the direct measurement quantities further cause the errors of the indirect measurement quantities.Suppose the indirect measurement quantity Y is the general function of the direct measurement quantities X1,X2,...,Xnas Eq.(A1).

The relative error of the indirect measurement is as follows:

As mentioned in Table A1,the absolute error of the mass flow rate is relevant to the measuring range of flowmeter.Experiment flowmeter range is 30 kg/h or 60 kg/h,and the relative error of mass flow rate under each condition is shown in Table A2.
The relative error of the Reynolds number is defined as follows according to Eq.(A3)and the detailed results are shown in Table A3:

Table A1 Errors of direct measurement quantities.

Table A2 Relative errors of mass flow rate.

Table A3 Relative errors of Reynolds number.

The relative error of the rotation number is described as follows and the detailed results are shown in Table A4:

The error of the local Nusselt number is as follows:

Thermal conductivity of air is a function of temperature,

Then the error of air thermal conductivity can be calculated as Eq.(A7):

Due to the large number of working conditions and measuring points,the detailed local Nusselt number error is not list here.
The relative errors of fanning friction factor are calculated as Eqs.(A8)-(A11)and list in Table A5.


Table A4 Relative errors of rotation number(Remain=12000).

Table A5 Relative error of lf ow resistance coefficient.

1.Han JC.Fundamental gas turbine heat transfer.J Therm Sci Eng Appl 2013;5(2):021007.
2.Han JC.Turbine blade cooling studies at Texas A&M University:1980–2004.J Thermophys Heat Transfer 2006;20(2):161–87.
3.Han JC,Huh M.Recent studies in turbine blade internal cooling.Heat Transfer Res 2010;41(8):803–28.
4.Lau SC,Han JC,Batten T.Heat transfer,pressure drop,and mass flow rate in pin fin channels with long and short trailing edge ejection holes.J Turbomach 1989;111(2):116–23.
5.Lau SC,Mcmillin RD,Kukreja RT.Segmental heat transfer in a pin fin channel with ejection holes.Int J Heat Mass Transfer 1992;35(6):1407–17.
6.Wright LM,Gohardani AS.Effect of coolant ejection in rectangular and trapezoidal trailing edge cooling passages.New York:ASME;2008.Report No.:GT2008-50414.
7.Kumaran TK,Han JC,Lau SC.Augmented heat transfer in a pin if n channel with short or long ejection holes.Int J Heat Mass Transfer 1991;34(10):2617–28.
8.McMillin RD,Lau SC.Effect of trailing-edge ejection on local heat(mass)transfer in pin fin cooling channels in turbine blades.J Turbomach 1994;116(1):159–68.
9.Taslim ME,Li T,Spring SD.Experimental study of the effects of bleed holes on heat transfer and pressure drop in trapezoidal passageswith tapered turbulators.J Turbomach 1995;117(2):281–9.
10.Hwang JJ,Lai DY,Tsia YP.Heat transfer and pressure drop in pin- fin trapezoidal ducts.J Turbomach 1999;121(2):264–71.
11.Hwang JJ,Lu CC.Lateral- flow effect on end wall heat transfer and pressure drop in a pin- fin trapezoidal duct of various pin shapes.New York:ASME;2000.Report No.:2000-GT-0232.
12.Kan R,Li Y,Ren J,Jiang HD.Effect of rib configuration and lateral ejection on a high aspect ratio trailing edge channel.New York:ASME;2013.Report No.:GT2013-94549.
13.Chang SW,Liou TM,Chiou SF,Chang SF.Heat transfer in highspeed rotating trapezoidal duct with rib-roughened surfaces and air bleeds from the wall on the apical side.J Heat Transfer 2008;130(6):142–50.
14.Wright LM,Liu YH,Han JC,Chopra S.Heat transfer in trailing edge,wedge-shaped cooling channels under high rotation numbers.J Heat Transfer 2008;130(7):135–45.
15.Liu YH,Huh M,Wright LM,Han JC.Heat transfer in trailingedge channels with slot ejection under high rotation numbers.J Thermophys Heat Transfer 2015;23(2):305–15.
16.Rallabandi AP,Liu YH,Han JC.Heat transfer in trailing edge wedge-shaped pin- fin channels with slot ejection under high rotation numbers.J Therm Sci Eng Appl 2011;3(2):021007.
17.Liu YH,Huh M,Han JC.High rotation number effect on heat transfer in a trailing edge channel with tapered ribs.Int J Heat Fluid Flow 2011;33(1):182–92.
18.Qiu L,Deng H,Tao Z.Effect of channel orientation in a rotating smooth wedge-shaped cooling channel with lateral ejection.New York:ASME;2013.Report No.:GT2013-94758.
19.Tao Z,Qiu L,Deng H.Heat transfer in a rotating smooth wedgeshaped channel with lateral fluid extraction.Appl Therm Eng 2015;87:47–55.
20.Srinivasan B,Dhamarla A,Jayamurugan C,Rajan AB.Numerical Studies on effect of channel orientation in a rotating smooth wedge-shaped cooling channel.New York:ASME;2014.Report No.:GT2014-26560.
21.Pardeshi I,Shih TI,Bryden KM,Ames R,Dennis RA,Ding S,et al.Flow and heat transfer in a rotating and non-rotating wedgeshaped cooling passage with ribs and pin fins.Reston:AIAA;2015.Report No.:AIAA-2015-1444.
22.Li Y,Xu G,Deng H,Qiu L,Yu X.Effects of coolant mass flow rate ratio on heat transfer in a two-inlet rotating wedge-shaped channel.Int J Heat Mass Transfer 2016;96:353–61.
23.Deng H,Qiu L,Tao Z,Tian S.Heat transfer study in rotating smooth square U-duct at high rotation numbers.Int J Heat Mass Transfer 2013;66:733–44.
24.Qiu L,Deng H,Sun J,Tao Z,Tian S.Pressure drop and heat transfer in rotating smooth square U-duct under high rotation numbers.Int J Heat Mass Transfer 2013;66:543–52.
25.Fu WL,Wright LM,Han JC.Rotational buoyancy effects on heat transfer in five different aspect-ratio rectangular channels with smooth walls and 45 degree ribbed walls.J Heat Transfer 2006;128(11):1130–41.
26.Cheng J,Ni B,Deng H.Experimental technique and its validation for heat transfer in cooling channels at high rotation numbers.J Aerospace Power 2014;29(8):1817–23[Chinese].
27.Deng H,Cheng HJ,Chen H,Tian S.Heat transfer in two-pass smooth square channel under large rotation numbers.J Beijing Univ Aeronaut Astronaut 2014;40(5):701–6[Chinese].
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Recent development of a CFD-wind tunnel correlation study based on CAE-AVM investigation
- Correlation analysis of combined and separated eあects of wing deformation and support system in the CAE-AVM study
- High-speed wind tunnel test of the CAE aerodynamic validation model
- Multi-infill strategy for kriging models used in variable fidelity optimization
- Numerical evaluation of acoustic characteristics and their damping of a thrust chamber using a constant-volume bomb model
- Scaling procedures of cabin noise generated by turbulent boundary layer excitation
