Multi-infill strategy for kriging models used in variable fidelity optimization

Chao SONG,Xudong YANG,Wenping SONG

National Key Laboratory of Science and Technology on Aerodynamic Design and Research,Northwestern Polytechnical University,710072 Xi’an,China

1.Introduction

With the development of CFD,the high- fidelity analyses have been employed in the aerodynamic design process.1,2As a result,an optimization method that requires a large number of function evaluations becomes computationally expensive. Surrogate model methods have attracted increased attention because the design efficiency can be improved dramatically,especially when a high- fidelity but time-consuming solver is employed.3A surrogate model can be used to replace expensive function evaluations by an analytic model,which is constructed with sample points by probing the design space randomly.Different types of surrogates have been developed for various purposes.Some are globally accurate in design space but require high computational cost to construct and evaluate.Other forms are locally accurate and computationally efficient,known as a trust region approach.They are very attractive for use in Surrogate-Based Optimization(SBO)methods.To further improve the efficiency of building a surrogate model,the Variable-Fidelity Modeling(VFM)isdeveloped,which allows a reduction of expensive high- fidelity computations with the enhancement of cheaper low- fidelity data.Kennedy and O’Hagan4developed an autoregressive model,which used the output of low- fidelity codes to enhance the prediction of high- fidelity codes.Forrester et al.5presented an aerodynamic design of a wing using correlated empirical and panel codes.Han and Gortz6proposed a Hierarchical Kriging(HK)model,which provides a reasonable Mean-Squared-Error(MSE)estimation.The MSE estimation is critical for error based sample point refinement in the context of variable- fidelity optimization.The variable- fidelity based analysis and optimization have been extensively used in aerodynamic designs.7–9

This study uses a two-stage approach,in which a surrogate model is built with given training samples.Then,the design space is searched based on this surrogate model according to a certain criterion,so called infill strategy.The new points identified by infill strategies are used to increase the chance of obtaining the optimum solution by refining the surrogate model.The infill strategy is the key issue of the SBO approach.Many infill strategies are available,10,11such as maximizing Expected Improvement(EI),maximizing the Probability of Improvement function(PI),minimizing the Lower Confidence Bounding(LCB),Minimizing the Prediction of surrogate models(MP),and maximizing the MSE.In many studies,just one infill criterion is used and only one sample point is obtained in an updating cycle.Actually,each commonly used infill criterion has pros and cons.11For example,the EI is the most favored criterion in kriging based optimization but the EI function is highly multimodal in high-dimensional problems.12Besides,it may take weeks to complete optimizations by adding only a single sample point per cycle.There is a strong incentive to overcome this limitation.Yao et al.13proposed a hybrid infill strategy,the surrogate,which used the LCB and Divergence form local Linear Interpolation(DLI)criterion,for neuralnetwork based optimization.Chaudhurietal.14applied a SBO approach with EI and PI criteria in the optimization of flapping wings.Laurenceau15chose 3 different sample points determined by the LCB at each updating cycle for airfoil and wing design.It has been proven that the multi-infill strategy for surrogate models is more efficient than single infill criterion.16

Although the multi-infill strategy tends to be mature,investigationsofmulti-infillstrategy forvariable- fidelity models have seldom been involved.Development of a high efficient SBO method that would take full advantage of the exploration and exploitation capability of infill criteria and the trend prediction form low- fidelity model is still an open problem.In this paper,a computationally efficient design methodology using the HK model and multi-infill strategy is proposed to reduce the cost for model construction and refinement.The paper is organized as follows.An overview of the variable- fidelity method used in this paper is presented first in Section 2.Next,a description of the multi-infill strategy is provided,as well as the optimization procedure.In Sections3 and 4,the multi-infillstrategy forthe variable- fidelity model is illustrated by an airfoil optimization case and a high-dimensional design case considering 63 design variables on a wing.Finally,conclusions are given in Section 5.

2.Methodology for aerodynamic shape optimization

2.1.Hierarchical kriging

The HK model provides a simple correction process which models the differences between the cheap and expensive data.A low- fidelity kriging model is constructed firstly to assist the prediction of the high- fidelity function.Actually,the lowfidelity model has the same form of function as an ordinary kriging,and it expresses the unknown function ylf（x）as follows:

where x is an m-dimensional vector of design variables.Thefirst term μlfis a global constant and the second term is a stationary random process,which creates a localized deviation from the global model.The stationary random process Zlf（x）represents a local deviation from the global model.It has mean zero and covariance of

where σ2is the process variance of Zlf（x）and R（x，x′）is the spatial correlation function.A popular correlation function is

where θk(θk＞ 0)and θpkare correlation parameters to be determined for constructing the kriging model,andandare the kth components of vectors xiand xj.

The low- fidelity kriging predictor for the values of x is obtained from

A high- fidelity function is given by

The HK predictor can be written as

The HK provides a better MSE estimation than traditional kriging,which is very helpful for error-based sample point refinement in the context of optimizations.Ref.6can be referred to for more information about the HK model.

2.2.Optimization procedure

An optimization method is proposed based on the HK model,which takes the benefits from the low- fidelity model and the multi-infill strategy.In a common VFM optimization method,the Design of Experiments(DoE)is needed to generate samples for both low- fidelity and high- fidelity model.It may be a waste of high- fidelity data if redundant sample points are employed.In the proposed method,only the initial lowfidelity model is constructed and no DoE is employed for the initial high- fidelity model construction.Before the iteration process,sample points are identified by the multi-infill strategy based on the low- fidelity model prediction.These sample points will be evaluated using the high- fidelity solver for the HK model construction.

The model updating method is the key aspect for the success of the optimization.It must represent a compromise between exploitation and exploration.In this approach,the EI,PI,LCB,and MP are used for each updating cycle,and totally 4 new samples are added.

The flowchart of the optimization is shown in Fig.1.Here,a set of sample points are obtained by Latin Hypercube Sampling(LHS)17only for the low- fidelity model construction.The computational cost can be saved due to the absence of evaluations for high- fidelity samples.In the first iteration of the optimization case,the infill sample locations are predicted based on the low- fidelity model due to the fact that the highfidelity model is unable to be constructed at this time.After an initial HK model is constructed,it will be updated by the multi-infill criteria to obtain a more accurate kriging model.Then the model is searched using a Genetic Algorithm(GA)to find the optimal design.The optimization process is stopped when the maximum iteration steps are reached or the objective function is not improved after 20 consecutive iterations.

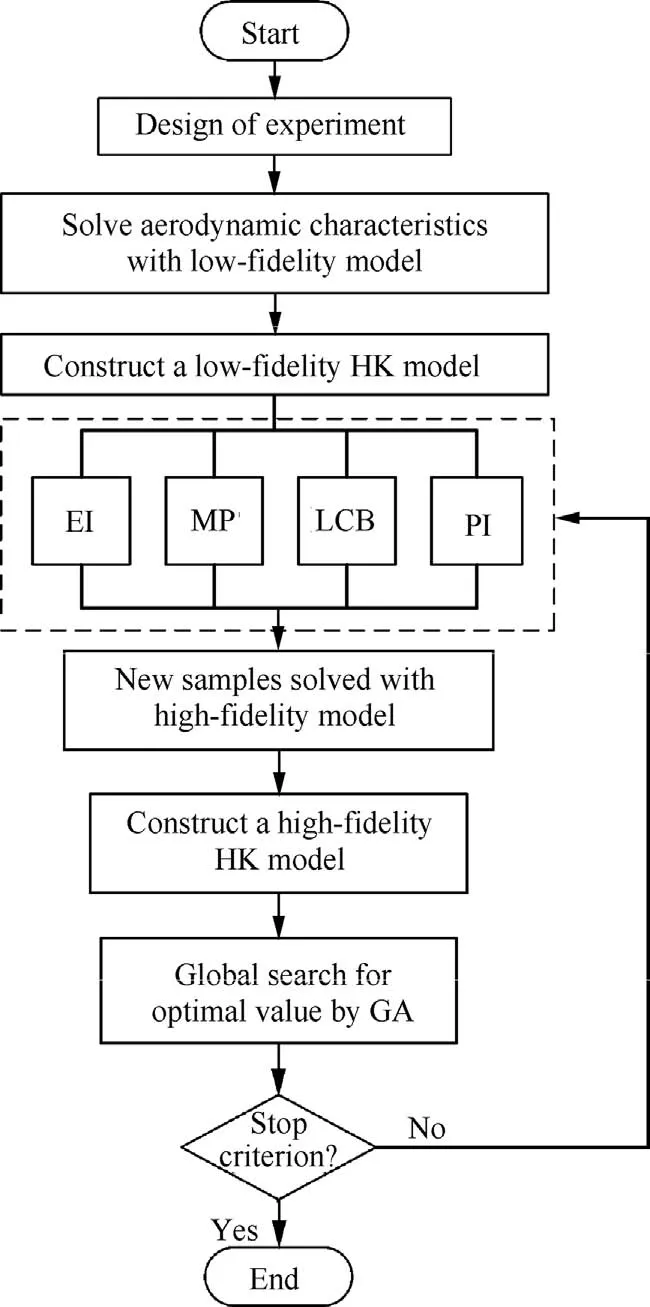
Fig.1 Flowchart of variable- fidelity optimization using multiinfill criteria.

2.3.Performance measurement of optimization methods

In order to evaluate the optimization methods,four criteria:improvement,computational cost,exploitation and exploration are defined.15The relative improvement of the objective function value is the main criterion,which is defined as

where Objiniis the objective function value of the baseline shape,and Objkis the function value at the kth iteration.The computational cost is the wall-clock time used for the optimization process.The criterion for the computational cost can be defined as 1/niter,where niteris the number of process iteration.

Balance between local search of promising solutions(exploitation)and global search within the entire design spaces(exploration)is one of the main concerns in global optimization algorithms.The optimizer may be trapped by the nearest local optimum before the design space has been explored sufficiently.However,over exploration is a waste of resources.Here,the exploitation criterion is defined as the ability of the optimization method to translate the information from function evaluations to the objective function improvement.It can be defined quantificationally as I/nevar,where nevaris the number of function evaluations in the optimization process.The exploration ability of the optimization method is measured by the distance between the best known design variables(xbest)and the de∑sign variables that have been explored(xe).It is expressed as‖xbest-xe‖/m,where m is the number of design variables.An optimization approach will be assessed from a compromise between the four criteria.

3.Transonic airfoil design case

In this section,the proposed approach was applied to an airfoil optimization problem to determine the shape with the minimum aerodynamic drag.The Mach number Ma was 0.8,and the angle of attack α was 1.25°.Both the geometry constraint and lift coefficient constraint were included in the objective function,and the optimization problem was defined as

where CDis drag coefficient,CLis lift coefficient,A represents the area for the airfoil and the subscript 0 indicates the value for the baseline airfoil.In order to improve the optimization efficiency,a low- fidelity model which can provide a suitable global trend for the high- fidelity HK model was to be determined.In this section,a coarse mesh was selected for the low- fidelity model.

The Stanford University Unstructured(SU2)software suite18has been used for the flow analysis.The high- fidelity sample points were obtained by solving the Euler equations with fine meshes,and the coarse meshes were used for lowfidelity data.The fine and coarse mesh around the airfoil consisted of 36909 and 3550 tetrahedral elements,respectively.The NACA0012 airfoil was used for the baseline airfoil.The surface meshes around the baseline airfoil for the high- fidelity and low- fidelity solutions are shown in Fig.2.The convective fluxes were computed with the Jameson-Schmidt-Turkel(JST)scheme.19Implicit local time-stepping was used to accelerate the problem converging to a steadystate solution.The wall-clock time for one high- fidelity flow simulation was about 35 s,and it was only 5.5 s for one lowfidelity simulation,using 2-core Intel i7(3.4 GHz)processors.

The airfoil shape was parameterized using the 4-order‘Class function/Shape function” Transformation(CST)technique,20resulting in 10 variables for the airfoil in total.100 sample points were selected by the LHS for the low- fidelity model construction.For comparison,the ordinary kriging based optimization refined by the multi-infill strategy and the HK based optimization using the EI were also carried out.Among many infill criteria,the EI infill criterion has been proved to be the best to find the global optimum.12The optimization method gets wide application in the aerodynamic design,which is by the name of Efficient Global Optimization(EGO).

The proposed optimization approach needs no DoE for the high- fidelity model.However,the ordinary kriging model is unable to be constructed without initial sample points.Thus 30 high- fidelity sample points selected randomly by the LHS were used for ordinary kriging model construction.The HK based optimization using the EI also employed the same high- fidelity samples to construct an initial high- fidelity model.Every test case was repeated for 10 independent times with randomly selected high- fidelity initial samples.Thus,the influence of high- fidelity samples could be eliminated.

Fig.2 Fine and coarse mesh around NACA0012 airfoil.

Fig.3 Averaged convergence histories of ordinary kriging and HK based optimizations.

Fig.3 represents the averaged convergence history of the optimization cases and the standard deviation of the optimal values.At the early stage of the optimization process,all objective values tend to converge rapidly.The HK model refined with the EI always keeps at a lower objective value than the ordinary kriging based optimization,although only one new sample point is added to the sample set.Taking the advantage of the low- fidelity model,a good trend prediction is provided for the HK model,and the optimization converges fast.The proposed approach employs both the low- fidelity model and the multi-infill strategy.It is the quickest to converge and less expensive due to being free of any initial sample requirement.

The averaged optimal value of the 10 independent runs of the ordinary kriging is 0.1775,with a standard deviation of 0.0256.The optimal value is further improved by the HK based optimizations employing the coarse mesh as a lowfidelity model.It is also important to note that the standard deviation is reduced evidently.The solving time of the lowfidelity solution is only about 15.7%of that using the fine mesh.Therefore,the optimization efficiency is further enhanced with such a coarse mesh.The combination of the low- fidelity model and the multi-infill strategy brings significant improvement of objective value,and reduction of iterations.

The performance characteristics of the three optimization methods are summed up in Table 1,using the criteria described previously.A bigger value in the table represents better performance.We can confirm again that the HK based optimization using multi-infill strategy outperforms the other methods in both objective function improvement and convergence speed.

When it comes to calculating the exploitation criterion,both the number of low- fidelity and high- fidelity sample evaluations are involved in nevar.A low- fidelity flow solution is considered to be 0.157 high- fidelity flow evaluation,according to the computation time.Although the proposed method needs only 44 iterations to complete the optimization process,4 different high- fidelity samples are evaluated in each updating cycle.Then the total number of equivalent flow solutions is 192 using the proposed method,and the HK model refined with the EI needs about 108 evaluations.As a result,the HK based optimization using the EI achieves higher exploitation value than the ordinary kriging and the proposed method.One can see here that there is no free lunch theorem for optimization,21and one has to pay more computational price in order to obtain a better solution.However,the multi-infill strategy is ready for parallel computation and the convergence speed can match with single infill criteria with sufficient resources.In other words,the advantage of the proposedmethod will be more evident when the infill strategy is carried out in parallel.

Table 1 Performance of optimization methods.

It is interesting to compare the exploration criteria of the three methods.The exploration value of the optimization using EI is much lower than the multi-infill strategy in the HK based optimizations.It indicates that the exploration ability is mainly contributed by the infill criteria.The ordinary kriging performs less exploration than the HK model,using the multi-infill strategy.This means that the low- fidelity model is also helpful for the exploration of the optimization method.

The aerodynamic performance of the baseline airfoil and the optimized airfoils obtained by different methods is reported in Table 2.In this table,the optimized airfoils are the best results of the 10 independent runs using different methods.Both the lift and the area of the optimized airfoils meet the condition of constraints.Using the ordinary kriging with multi-infill strategy,the drag is reduced by 85.7%,whereas the HK based optimization with EI method and the multi-infill strategy further reduces it by 86.6%and 86.7%,respectively.In Fig.4,the optimized shapes using different methods are represented.There are noteworthy differences between the shape obtained by the ordinary kriging and the HK based optimizations.This illustrates that the aerodynamic optimization is a multimodal problem and the ordinary kriging based optimization may be trapped in a local optimum.Fig.5 shows the pressure coefficient Cpof the baseline and the optimized shapes.The pressure distribution on the baseline airfoil shows the presence of a shock at the upper surface.This shock is suppressed by the deformations proposed by the optimizer,and thus the drag is reduced significantly.As we can see in thefigure,the strength of the shock wave on the optimized airfoil obtained by the proposed method is the weakest,corresponding to the lowest drag level.

4.High-dimensional wing design case

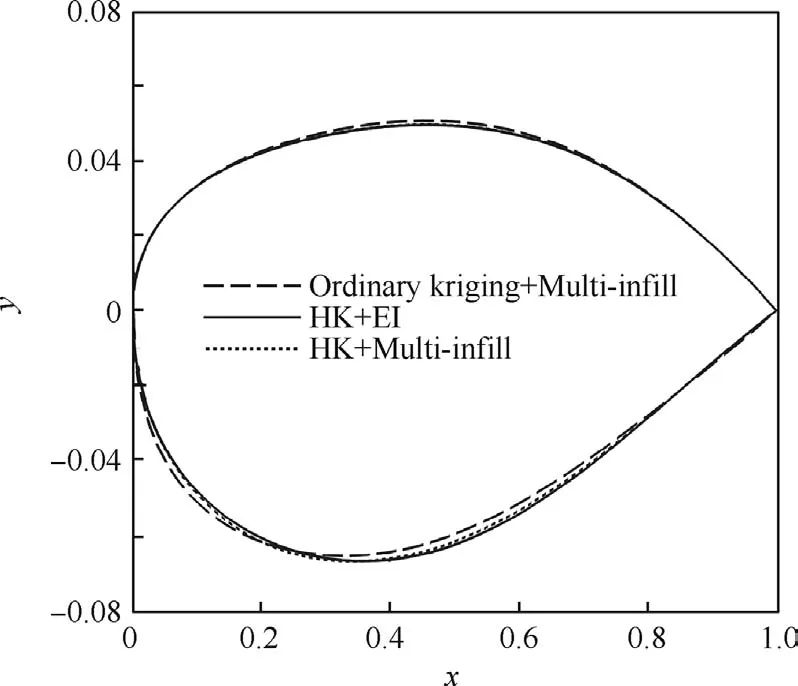
Fig.4 Optimized shape using different methods.

Fig.5 Pressure coefficients on surface of baseline airfoil and optimum designs.

The ONERA M6 wing was used for the baseline wing.The objective function considered was the aerodynamic drag subject to the lift of the baseline configuration,at a Mach number of Ma=0.8395 and an angle of attack of 3.06°.The SU2software suite has been used for the flow analysis.The highfidelity sample points were obtained by solving the RANS equations.The convective fluxes were computed with the second-order Jameson’central scheme19and the Spalart-Allmaras turbulence model22was solved for turbulence flow simulation.Implicit local time-stepping was used to accelerate the problem converging to a steady-state solution.The unstructured mesh around the ONERA M6 wing consisted of1051036 tetrahedral elements for Reynolds-Averaged Navier-Stokes(RANS)equations solutions.The wall-clock time for one high- fidelity flow simulation was more than 1 h,using 2-core Intel i7(3.4 GHz)processors.

Inviscid Euler simulation results were solved using the similar manner as the low- fidelity data and the Euler mesh consisted of 582752 elements.An Euler solution can be quickly resolved with only about 3 min.The surface meshes for the RANS and Euler solutions are shown in Fig.6.

Fig.7 shows the computational pressure coefficient distributions from SU2and the wind-tunnel experimental data23,under the free-stream condition of Ma=0.8395，Re=11.72 × 106，α =3.06°.The RANS simulation can get better accordance with the experimental results at the 44%and 90%span-wise station of the wing than the Euler simulation.

In this three-dimensional design case,a Free-Form Deformation(FFD)24strategy has been adopted.A set of control points were defined on the surface of the box,and the shape inside the FFD box was controlled by these control points.In this case,only movements in the vertical direction for the upper surface were allowed,and there were a total of 63 control points as shown in Fig.8.Once the deformation has been applied,a classical spring method was used in order to deform the rest of vertices of the mesh.25

Fig.6 Meshes for RANS and Euler solutions.

Fig.7 Comparison of pressure distribution between experimental results and SU2simulations.

Fig.8 Control points of FFD box(spherical symbols).

Fig.9 Convergence history of objective function of optimization process.

In this section, theHKbased optimizations using the EI infillcriterion and the multi-infill strategy were carried out to demonstratethe effectiveness of the multi-infill strategy. The ordinarykriging model with the multi-infill strategy was also employedfor the optimization case to show the advantage of the lowfidelitymodel. Both the sampling and infilling processes werecarried out in parallel in this section due to expensive numericalRANS simulations. Totally 300 low-fidelity sample points wereselected by the LHS. The number of initial high-fidelity samplepoints was 100 for HKbased optimization using the EI and ordinarykriging using the multi-infill strategy.

Fig.9 represents the convergence history of each optimizer.The ordinary kriging needs more iterations to converge to its final value,compared with the HK model.The HK based optimization using the EI achieves a relatively low value by less iterations.However,it converges slower than the optimization using both the low- fidelity data and the multi-infill strategy.It is noteworthy that the HK based optimization using the multi-infill strategy reached a plateau within only 24 iterations,even without any initial highfidelity sample.At the same time,a significant improvement of the function is achieved.Another further benefit of the multi-infill strategy is easy to implement for parallel computation.As the design case in this section,the optimization requires a large amount of computation time for highfidelity computer simulations.Table 3 shows that the wall clock time for the flow solutions of DoE and infilling process using different optimization methods.The ordinary kriging based optimization takes about 3 days and needs 48 iterations to complete the whole process,including the cost of sampling for the initial model construction.Because the multi-infill strategy is applied in parallel and the optimization process needs around 24 iterations to converge,the wall-clock time for high- fidelity solutions is only about 26 h.It means that more than 60%computational time can be saved compared with the ordinary kriging based optimization.

Table 3 Wall-clock time for optimization process using different methods.

Fig.10 Comparison of airfoil shapes and pressure distributions of 2 span-wise sections of baseline and optimized wing.

Fig.11 Comparison of pressure contours on baseline and optimized wing obtained by HK based optimization using multiinfill strategy.

Table 4 Aerodynamic performance of baseline and optimized shapes.

Fig.10 presents the airfoil shapes and the associated pressure distribution for the span-wise sections of the baseline and the optimized wings.A shock wave appears on the upper surface of the baseline configuration.As we can see in Fig.10(b)and(d),the shock on the baseline shape is strong,and it is attenuated evidently by the deformations proposed by the optimizer.The deformation of the section shape on 90%semi-span is more obvious.By reducing the camber near the leading edge,the flow velocity deceases on the upper surface and the shock strength is reduced.Although all optimizers find different shapes and are able to reduce the strength of the shock,the shock wave on the shape obtained by the proposed method is the weakest.Therefore,the objective function converges to the lowest level.Fig.11 shows the pressure contours on the upper surface of the baseline and the optimized wing shape obtained by the proposed method.It can be concluded again that the optimizer leads to the shape with weak shocks,as can be verified on the pressure contours on the wing skin.

In terms of improvement of the objective function(Table 4),the HK based optimizers largely outperform the ordinary kriging.Both the HK based optimizations using the EI and multiinfill strategy give close results in terms offinal optimum objective value.It confirms that the low- fidelity model is able to provide a good model prediction for the global trend.The drag is decreased by 12.2%,using the multi-infill strategy,which is a little better result than the result obtained using the EI infill criterion only.It confirms the enhanced exploration and exploitation capabilities of the multi-infill strategy.

5.Conclusions

A highly efficient optimization approach has been proposed based on the HK model using the multi-infill strategy.The developed approach takes full advantages of low- fidelity model and multiple kinds of infill criteria.A large amount of highfidelity evaluations for initial model construction are no more needed and the optimization process is speeded up evidently.

(1)In the airfoil design case,a coarse mesh is able to enhance the HK model prediction.Compared with the ordinary kriging using the multi-infill strategy and HK using the EI method,an optimum design is found without DoE for high- fidelity model using the proposed method.It outperforms the other methods largely in terms of objective function improvement,convergence speed,and exploration ability.Despite the fact that the proposed method needs more high- fidelity function evaluations to find a better optimum design,the multi-infill strategy is ready for parallel computation and the wall clock time can be equivalent to the EI method.

(2)The proposed method is applied to a high-dimensional wing design case considering 63 design variables.It is free of the time-consuming high- fidelity sampling process,and converges quickly with much less iterations.As a result,more than 60%computational cost is saved compared with the ordinary kriging using the same infill strategy.Besides the improvements in design efficiency,a better optimization is obtained.The enhanced exploration and exploitation capabilities of the proposed method are confirmed by the high-dimensional design case.

(3)The developed approach is promising for efficient design optimization,especially when computational expensive evaluations or high-dimensional design problems are involved.The significant improvement of the optimization efficiency allows a faster overall design process,while produces better final designs.

This study was co-supported by the National Natural Science Foundation of China(Nos.11272263 and 11302177).

1.Lu WS,Tian Y,Liu PQ.Aerodynamic optimization and mechanism design of flexible variable camber trailing-edge flap.Chine J Aeronaut 2017;30(3):988–1003.

2.Zhao K,Gao ZH,Huang JT,Li Q.Aerodynamic optimization of rotor airfoil based on multi-layer hierarchical constraint method.Chin J Aeronaut 2016;29(6):1541–52.

3.Jeong S,Murayama M,Yamamoto K.Efficient optimization design method using kriging model.J Aircraft 2005;42(5):413–20.

4.Kennedy M,O’Hagan A.Predicting the output from a complex computer code when fast approximations are available.Biometrika 2002;87(1):1–13.

5.Forrester AIJ,So´bester A,Keane AJ.Multi- fidelity optimization via surrogate modeling.Proceed Roy Soc A:Math,Phys Eng Sci 2007;463(2088):3251–69.

6.Han ZH,Gortz S.Hierarchical kriging model for variable- fidelity surrogate modeling.AIAA J 2012;50(9):1885–96.

7.Kwon HI,Yi S,Choi S,Kim K.Design of efficient propellers using variable- fidelity aerodynamic analysis and multilevel optimization.J Propul Power 2015;31(4):1057–72.

8.Moore J,Stanford B,McClung A,Beran P.Variable- fidelity kinematic optimization of a two-dimensional hovering wing.49th AIAA aerospace sciences meeting including the new horizions forum and aerospace exposition.Reston:AIAA;2011.

9.Siegler J,Ren J,Leifsson L,Koziel S,Bekasiewicz A.Supersonic airfoil shape optimization by variable- fidelity models and manifold mapping.Procedia Comput Sci 2016;80:1103–13.

10.Forrester AI,Keane AJ.Recent advances in surrogate-based optimization.Prog Aerosp Sci 2009;45(1):50–79.

11.Liu J,Han ZH,Song WP.Efficient kriging-based aerodynamic design of transonic airfoils:some key issues.50th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition.Reston:AIAA;2012.

12.Jones DR, Schlonlau M, Welch WJ. Efficient global optimizationof expensive black-box functions. J Global Optim 2008;13(4):455–92.

13.Yao W,Chen XQ,Huang Y,Tooren MV.A surrogate-based optimization method with RBF neural network enhanced by linear interpolation and hybrid infill strategy.Opt Methods Softw 2013;29(2):406–29.

14.Chaudhuri A,Haftka RT,Ifju P,Chang K,Tyler C,Schmitz T.Experimental flapping wing optimization and uncertainty quantification using limited samples.Struct Multidiscip Optim 2014;51(4):1–14.

15.Laurenceau J,Meaux M,Montagnac M,Sagaut P.Comparison of gradient-based and gradient-enhanced response-surface-based optimizers.AIAA J 2010;48(5):981–94.

16.Liu J,Song WP,Han ZH,Zhang Y.Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models.Struct Multidiscip Optim 2017;55(3):925–43.

17.McKay MD,Beckman RJ,Conover WJ.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code.Technometrics 2000;42(1):55–61.

18.Palacios F,Economon TD,Aranake A,Copeland SR,Lonkar AK,Lukaczyk TW,et al.Stanford university unstructured(SU2):Analysis and design technology for turbulent flows.52nd aerospace sciences meeting.Reston:AIAA;2014.

19.Jameson A,Schmidt W,Turkel E.Numerical solutions of the euler equations by finite volume methods using runge-kutta timestepping schemes.14th fluid and plasma dynamics conference.1981.

20.Kulfan BM.Universal parametric geometry representation method.J Aircraft 2008;45(1):142–58.

21.Wolpert DH,Macready WG.No free lunch theorems for optimization.IEEE Trans Evol Comput 1997;1(1):67–82.

22.Spalart PR,Allmaras SR.A one equation turbulence model for aerodynamic flows.30th aerospace sciences meeting and exhibit.Reston:AIAA;1992.

23.Schmitt V,Charpin F.Pressure distributions on the ONERA-M6-wing at transonic Mach numbers.Paris:AGARD;1979.Report No.:AGARD-AR-B1-20.

24.Sederberg TW,Parry SR.Free-form deformation of solid geometric models.ACM SIGGRAPH Comput Graph 1986;20(4):151–60.

25.Degand C,Farhat C.A three-dimensional torsional spring analogy method for unstructured dynamic meshes.Comput Struct 2002;80(3):305–16.