Modal characteristics analysis for a flexible rotor with non-smooth constraint due to intermittent rub-impact

Jie HONG,Pingcho YU,Dyi ZHANG,*,Zhicho LIANG

aSchool of Energy and Power Engineering,Beihang University,Beijing 100083,PR China

b Collaborative Innovation Center of Advanced Aero-Engine,Beihang University,Beijing 100083,PR China

1.Introduction

The high performance requirements for modern aero-engines always bring about the decrease of the clearance between rotors and stators,which probably results in the terrible rubimpact during operation.1Rub-impact is mostly a secondary failure for aero-engines2,which may result from misalignment,unexpected imbalance,blade off,etc.When rub-impact occurs,severe vibration can be induced to the machinery,which can lead to the permanent bow of the shaft,and even damages to the whole system.3As a result,the rotor-to-stator rubimpact has always been the crucial problem affecting the reliability and integrity of aero-engines,and it is extremely beneficial to study the vibration characteristics for the dynamics analysis and safety design of the aero-engine rotor systems.4–6

Rub-impact involves several physical phenomena,such as the most notable impact,friction and a stiffness increase while the contact is maintained,and as a result,the system turns to be highly nonlinear.7During the past decades,a significant amount of researches have been done on the mechanisms and the complicated phenomena of rub-impact,and some representative works include the thermal effects8–10,the possible dynamic behavior and corresponding response characteristics,the destructive dry-whip and its stability,and the stiffening effects.

Dynamic behavior of the rotor system excited by the impact force is one important research topic mentioned in many public references.Beatty introduced the piecewise linear rubimpact force model and investigated typical characteristics of rub-impact fault11for the first time.After his pioneering work,Choy et al.performed a detailed theoretical investigation to observe the effects of the casing stiffness,friction coefficient,etc.on the rub force and rotor orbit.12Goldman and Muszynska studied the dynamics of rotor systems with partial rubimpact.The orderly harmonic responses,sub-harmonic responses as well as chaotic responses were obtained in their simulation.13Chu and Zhang14investigated the non-linear vibration characteristics of a rub-impact Jeffcott rotor.They also found that when the rotating speed was increased,the grazing bifurcation,the quasi-periodic motion and chaotic motion occurred after the rub-impact.Ma et al.studied the rubbing-induced vibration responses based on contact dynamics theory,under different rubbing types such as single-point rubbing15,multi-point rubbing16,and full annular rubbing.17Some interesting fault features had also been extracted.Taking single-point rubbing as an example,different rotor motions,such as period-one motion P1,P2 and P3,could be observed with the increasing rotation speeds.15

Another emphasis of the researches is about the dry-friction whip and whirl characteristics of the rub-impact rotor system caused by the tangential friction force.During dry-friction whirl and whip,the rotor undertakes very large deformation and is subjected to high-frequency stress,which will initiate the break or the fatigue damage of the shaft and cause the failure of the machine.18In order to investigate dry-friction whirl,Black built a general model for synchronous rubbing and concluded that dry-friction whirl was only possible in the frequency band,extending from an individual rotor/stator natural frequency to the next higher combined system frequency.19Applying Black’s model to a long-cantilevered disk,Zhang20accounted for multiple rotor modes in dry-friction whip and whirl and identified the same whirl regions as Black.19,20Jiang and Ulbrich presented a modified Jeffcott rotor with a given rotor/stator clearance and cross-coupling influences and carried out an analytical study on the stability of the full annular rubbing conditions.18Childs and Kumar developed analytic dry-friction whip and whirl solutions for a rigid-rotor/rigid-stator model with contact at two rubbing locations.21

On the other hand,the influence of stiffening effects for rub-impact is also investigated by many researchers.The stiffening effect,also called constraint effect in Ref.22,is the phenomenon that rotor’s displacement is constrained and the stiffness of rotor system increases when rotor contacts with stator during rub-impact.Making use of this characteristic,Chu and Lu analyzed the change of transient stiffness of rotor quantitatively based on parameter identification theory and put forward an effective method to detect the rubbing positions.23,24Generally,rubbing forms determine the constraint stiffness change process of rubbing rotor.In rotor system,the rubbing forms mainly include full annular rubimpact17,20and intermittent rub-impact.16,17,25Full annular rub-impact denotes that the rotor is in continuous contact with the stator17,and consequently,constraint effect exists all the time.Ma et al.built a constraint mechanical model of full annular rub-impact and their study showed that constraint effect made the rotor’s resonant range expand.22Intermittent rub-impact,during which the contact between rotor and stator is characterized by a ‘bouncing”or intermittent type of behavior25,is one of the most common rubbing forms in rotor system.Due to the contact and separation of rotor with stator,constraint effect at that time is discontinuous and stiffness of rotor system is time-varying.As ‘discontinuous” is named‘non-smooth” in non-smooth mechanics26,this reference names the constraint effect or stiffening effect of intermittent rub-impact as ‘non-smooth constraint”.Bently demonstrated experimentally that intermittent rub-impact causes a periodic variation in the rotor’sstiffness,which could lead to Mathieu-Hill type of parametric instability.27Childs built a simple physical model and presented analysis of rotor’s dynamic characteristics and stability by this kind of rubinduced parametric excitation.28Abuzaid et al.investigated effect of intermittent rub-impact on rotor’s shaft vibration experimentally and analytically.In their study,rotor’s stiffness with the influence of non-smooth constraint was analyzed and a new additional stiffness model considering time-varying characteristic was proposed.29

In the literatures described above,researchers mostly focused on the dynamic behavior and vibration response characteristics of rubbing rotor system excited by impact and friction forces.However,the discussion on the modal characteristics of intermittent rub-impact rotor system with non-smooth constraint was rarely reported so far.The additional constraint produced by the rub-impact has been preliminarily discussed in the authors’previous researches2,in which the mechanism of the additional constraint is confirmed by an extremely simplified method;however the effects of non smooth constraint on rotor modal characteristics,particularly on the rotor’s stability,are not well studied.Meantime,it is also not well understood how the modal characteristics influence the rotor’s vibration response.In view of the above mentioned work, this paper further studies the modal characteristics of an overhung flexible rotor system with non smooth constraint more detailedly and systematically.A non-smooth constraint stiffness model is proposed based on the physical process of intermittent rub-impact,and the dynamic equation for an overhung rotor with non-smooth constraint is established.The time-varying parameters analysis method developed by Floquet theory and Hill’s method is described and used to obtain the modal characteristics of a non-smooth constraint rotor.Moreover,the influence of non-smooth constraint on the rotor response is obtained from the view of modal characteristics,and related experiments are performed to validate the theoretical results.

2.Theoretical study for rotor system with non-smooth constraint

In this section,the non-smooth constraint caused by the intermittent rub-impact is described,the corresponding modeling method is given,and the governing equations to describe the rotor behavior are established.Based on these results,the analysis method is developed by Floquet theory and Hill’s method to obtain the modal characteristics of a non-smooth constraint rotor.

2.1.Qualitative description for non-smooth constraint

The physical process of intermittent rub-impact could be described as Fig.1,In the figure,O and Ocare the centroids of the stator and rotor respectively,ω is rotation speed of the Jeffcott rotor and t is time.Firstly,the rotor collides the stator and then they contact for some time under the excitation of external loads.The permeating depth between the rotor and the stator will increase until a certain maximum value during the contact,and then the rotor rebounds apart from the stator.The above behavior repeats as periodic or quasi-periodic,and the friction always plays an important role during these processes due to the rotor-to-stator relative slip at the contact point.

In the process of intermittent rub-impact,repeated radial impact and contact not only provide a sort of widefrequency excitation on rotor,but also restrain the rotor’s lateral displacement.The latter will increase the radial stiffness of the rotor system.7,30This constraint effect could be regarded as an additional support,as shown in Fig.2.As already stated in the introduction,this kind of constraint effect is named as‘non-smooth constraint”in this article,for the reason that the constraint is discontinuous and behaves as non-smooth with the change of the rotor vibration amplitude.The increase of radial stiffness will result in unpredicted natural frequencies and eigen-mode modifications.Moreover,we should note that the repeated contact and separation between rotor and stator lead to a periodic variation for the rotor’s radial stiffness,and hence the constraint effect possesses time-varying characteristics,which may lead to parametric instability.28

Fig.1 Assumed physical process of intermittent rub-impact.

Fig.2 Non-smooth constraint caused by repeated radial impact.

Fig.3 Sketch of a typical LP rotor in aero-engine.

The influence of constraint effect on rotor system is mainly determined by the ratio between average constraint stiffness k’and equivalent stiffness of the rotor k at the rubbing position.The equivalent stiffness is defined as k=F/x31,where F and x are the static force and deformation at the corresponding position,respectively.If k′/k was minimal,the constraint effect produced during the process of repeated radial impact could be ignored due to the fact that this constraint affects little on the rotor system.However,if k′is closer to or higher than k,the constraint affects the rotor’s critical speeds and mode shapes significantly,and the constraint effect must be considered.Taking the aero-engine Low Pressure(LP)rotor as an example(Fig.3),the bending stiffness of the LP rotor is extremely low because of its long span between supports and its slender shaft.The constraint effect is remarkable and must be considered when rub-impact happens on it.

2.2.Dynamic modeling for a rotor system with non-smooth constraint

2.2.1.Mathematical description for non-smooth constraint

In the process of intermittent rub-impact,the constraint effect has time-varying features caused by the repeated radial impact and contact.Actually the constraint effect is very complex;however its key mechanical parameters could be extracted according to the rubbing physical process(Fig.1),and as a consequence,the parameters are summarized as the contact time,rubbing frequency and constraint stiffness amplitude.A simplified constraint model is established considering the above parameters and also their time-varying features,as shown in Fig.4.The stiffness curve during the rotor-tostator contact process is assumed to be a sine function for this modeling,and the formula for the stiffness is given as Eq.(1),whereis the maximum value for the constraint stiffness,called as constraint stiffness amplitude in this article;Tkis the rubbing period,which is equal to the constraint stiffness variation cycle;α is the ratio of the contact time over the rubbing period Tk,representing the contact duration during one rubbing period.T is the rotor rotation period.The ratio of Tk/T indicates the amount of rubbing times in one rotation period,for example,if the value was 1 or 1/2,the rotor rubs with stator for one time or two times in one rotation period.

Fig.4 Parameters to describe additional constraint stiffness.

2.2.2.Dynamic governing equation for non-smooth constraint rotor

An overhung fan rotor with multiple bearings,whose configuration and dynamical characteristics are similar to a typical LP rotor of the high bypass ratio gas turbine engine,is used in this study,as shown in Fig.5,blade-disk mass md=123 kg,polar inertia of blade-disk Jp=8 kg·m2,diameter inertia of bladedisk Jd=4 kg·m2,Elastic modulus E=2.1 × 105MPa,density ρ =7800 kg·m-3,Possion’s ratio μ =0.3,damping ratio ξ=0.1,shaftlengthl=2000 mm,l1=300 mm,l2=300 mm,l3=1400 mm,outer diameter D1=160 mm,D2=160 mm,D3=80 mm,inner diameter d1=140 mm,d2=140 mm,d3=70 mm,support stiffness k1=k2=k3=5=×=107=N·m-1.The non-smooth constraint is applied to the fan.The rotor’s parameters are also given in Fig.5.Finite element method is used to establish the dynamic governing equation of the model.The shaft is divided into 6 Timoshenko beam elements and 7 nodes.The blade and disk of fan are modeled using lumped mass elements.The bearings are simplified as linear stiffness and linear damping,and meanwhile,the non-smooth constraint model built in previous section is superimposed on the corresponding nodes.Eventually,the dynamic governing equation of the model is given as

where M,C,G,K,q and f（t）denote the mass matrix,the damping matrix,the gyroscopic matrix,the stiffness matrix,the displacement vector and the external force vector(mainly including the unbalance force)of the global system respectively.Here,the stiffness matrix K includes the rotor stiffness and the bearing stiffness,and the damping matrix C includes the bearing damping and the viscous damping of the rotor.Rayleigh damping form is applied to determining the damping matrix and it is obtained by the formula C=,where¯α and¯β can be obtained based on Ref.32.Ks（t）is the nonsmooth constraint stiffness matrix and has the periodic timevarying characteristics according to the model as shown in Fig.4.

2.3.Analytical method for modal characteristics

When the modal characteristics of the rotor system are analyzed,the external excitation force f（t）is ignored and the homogeneous equation is obtained:

Due to time-varying characteristics of constraint stiffness,there exist some differences for modal characteristics of nonsmooth constraint rotor system and the general linear rotor system.According to the Floquet theory,the solution of Eq.(3)can be written as

Fig.5 Overhung rotor and its configuration parameters.

where λ is the quasi eigenvalue,and Φ is the quasi modal vector which is periodically time-varying.Remarkably,variation period of quasi-mode Φ is equal to that of non-smooth constraint stiffness Ks（t）.

Considering the periodically time-varying features of Φ and Ks（t）,they can be expanded as the following Fourier forms:

where ljis the jth-order component of Φ（t）,and Ks，pis the pthorder component of Ks（t）.

By substituting Eqs.(5)and(6)into Eq.(3),it can be written as

where ωk=2π/Tk.

In Eq.(7),the coefficients’summation of the same index terms is equal to 0,and then an infinite determinant is obtained:

Firstly,the modal truncation must be adopted for Eq.(8)to transform it into finite term,and then modal frequencies can be obtained through eigenvalue solution of the finite determinant.Remarkably,the accuracy of solution is dependent on the number of modal truncation term j.We can choose an appropriate value of j by comparing the results under different values of j.When the eigenvalue solutions do not change obviously for the increase of j,we could reach the appropriate results.The number of modal truncation term j is chosen as 4 in the following study.

According to the Fourier forms stated in Eq.(5),the modal frequencies acquired from Eq.(8)can be expressed as

Eq.(9)shows that the modal frequencies of the non-smooth constraint rotor system are a set of values around ωn，0,and the difference of adjacent frequencies is rubbing frequency(constraint stiffness variation frequency) ωk.Here ωn，0is the nth-order main modal frequency of the system,also called as the nth-order normal modal frequency,which is corresponding with the nth modal frequency of the rotor without non-smooth constraint,and ωn，j（j=...，-1，1，...）is the jth harmonic frequency of the nth-order mode,produced by the non-smooth constraint stiffness.33

For each mode,the stability is determined by the real parts of the corresponding eigenvalues.The stable condition for the nth-order mode can be expressed as

The mode will be instable if the real parts of either harmonics in its family are greater than 0.Thus,the computation of eigenvalues of Eq.(8)truncated to a jmaxorder for each rotation speed implies the stability of modes.33

3.Modal characteristics of non-smooth constraint rotor system

3.1.Modal frequency

3.1.1.Rotor system without non-smooth constraint

In order to analyze the influence of the non-smooth constraint,modal frequencies of rotor system without the non-smooth constraint are calculated firstly.Parameters of the rotor model are shown in Fig.5,and critical speeds and corresponding modes are displayed in Fig.6.

The first critical speed is 48.1 Hz(2886 r/min),and its corresponding mode is overall bending of the rotor.The second critical speed is 151.9 Hz(7310 r/min),and its corresponding mode is the shaft bending between the support 2#and the support 3#.As the vibration displacement at fan edge is much smaller for the second mode(Fig.6(b))than that of the first mode(Fig.6(a)),the rubbing effects will be limited for the second mode.Therefore,only the results related to the first mode are studied in the following.

3.1.2.Rotor system with non-smooth constraint

When the non-smooth constraint is applied to the fan,modal frequencies of the rotor during the increase of rotation speed are calculated,as shown in Fig.7.According the theory in Section 2.3,there exist 9 modal frequencies aiming to the 1st order modal frequencies of the rotor system,i.e.1 normal modal frequency and 8 harmonic modal frequencies.Due to the fact that the normal mode indicates the traditional linear mode and usually dominates the rotor’s response,only the results of the normal modal frequencies are depicted.The identification of the normal modal frequency is based on the relationship between the normal modal frequency and harmonic modal frequencies,as shown in Eq.(9).In the calculation,the constraint stiffness amplitude~ksis given as 5×107N/m,which is equal to the stiffness of support 1#,i.e.for the upper curve in Fig.7.The contact time ratio α in one stiffness variation cycle is 0.8,and the rubbing periods are T,T/2 and T/3 which mean that the rotor rubs with stator for once,twice and three times in one rotation period,respectively.Besides,the modal frequencies of the rotor without constraint and with the maximum constraint are also presented in Fig.7.

Fig.7 exhibits several interesting phenomena.First of all,when the non-smooth constraint is applied to the rotor system,the modal frequencies will increase.The values of modal frequencies are within the interval defined by the rotor without non-smooth constraint and with the maximum constant constraint.Critical speeds also increase significantly by the effects of non-smooth constraint,and the critical speed interval for this case is between 5000 r/min and 5800 r/min.Secondly,with the increase of rotation speed,the change trend of modal frequencies for non-smooth constraint rotor system is fluctuant,especially at high rotation speeds,which is quite distinct from the monotonous change trend for the linear rotor modal.That is due to the time-varying characteristics of constraint stiffness.At lower rotation speeds,the rubbing frequencies are small and the constraint stiffness is almost constant,and thus the effects of rubbing frequencies can be negligible and the modal frequencies change gradually.On the other hand,at higher rotation speeds,the rubbing frequencies are higher and the time-varying characteristics of constraint stiffness are obvious;therefore the modal frequencies are not only dependent on the constraint extent but also the rubbing frequency,and as a consequence,the modal frequency changes fluctuant.Moreover,as the rubbing frequencies increase(from 1/T to 3/T),the fluctuant range of modal frequencies expands significantly from original[85.8,95.3]Hz to[64.5,100]Hz.Thirdly,at low rotation speeds(0–2000 r/min for this case),modal frequencies under different numbers of rubbing times are very close,which means that modal frequencies are not sensitive to the numbers of rubbing times.However at high rotation speeds,the influence of the rubbing frequencies is remarkable mainly because the rubbing frequencies at high rotation speeds are higher.

Fig.7 Campbell diagram for rotors with/without non-smooth constraint.

Furthermore,the influence of constraint stiffness parameters on modal frequencies under different rotation speeds is calculated,as shown in Fig.8.To clearly distinguish whether the rotor is under subcritical status or under supercritical status,the rotation speed ratio λ is employed and defined as ω/ω1,and here ω1is the first critical speed for the rotor without non-smooth constraint,i.e.48.1 Hz(2886 r/min).When λ is smaller than 1.0,the rotor operates under subcritical status.Subcritical rotation speeds 28.87 Hz(1732 r/min,λ=0.6),38.48 Hz(2309 r/min,λ=0.8)and supercritical rotation speeds 57.72 Hz(3463 r/min,λ=1.2),67.33 Hz(4040 r/min,λ=1.4)are selected.The rubbing period Tkis T/2.Fig.8(a)shows how the constraint stiffness amplitude affects the rotor modal frequencies.The contact time ratio α here is 0.8.The results are shown as follows:

Fig.6 Critical speeds and modal shapes of rotor system.

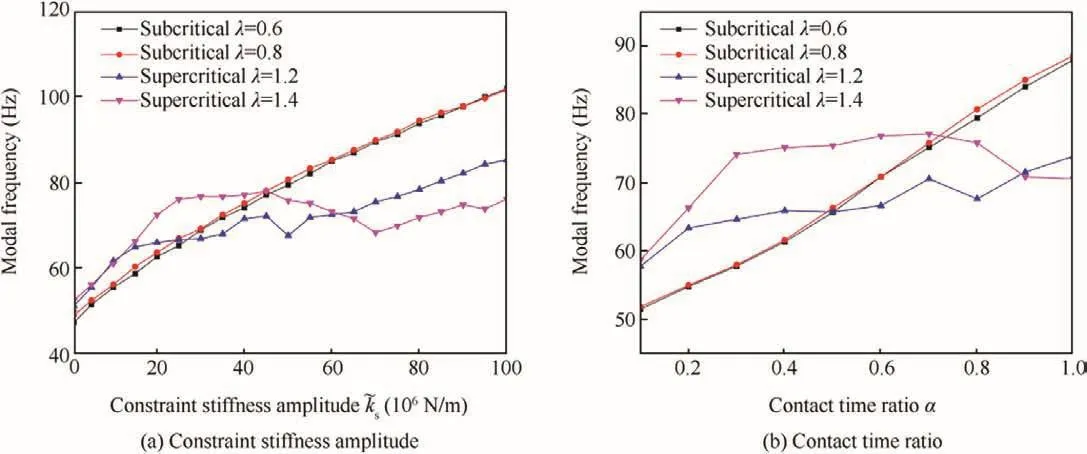
Fig.8 influence of constraint stiffness on modal frequencies for different rotation speed ratios.

(1)The modal frequencies both under subcritical status and under supercritical status increase with the increase of the constraint stiffness amplitude.However,the modal frequencies under subcritical status increase more obviously than those under supercritical status,which indicates that constraint stiffness amplitude plays a more important role on the modal frequencies of a rotor operating under subcritical status.

(2)The variation of modal frequency may exhibit some differences under different rotation speeds.For rotor in subcriticalrotation speeds,themodalfrequencies increase monotonically,whereas in supercritical rotation speeds the modal frequencies have fluctuant change,especially when constraint stiffness amplitude exceeds 4×107N/m.It is possibly because the modal frequencies are determined by both the constraint stiffness amplitude and rubbing frequency as the contact time ratio is fixed.When the numbers of rubbing times in one period are same,for the subcritical rotor,the corresponding rubbing frequencies are relatively lower,and then the modal frequencies are mainly affected by constraint stiffness amplitude.However for the supercritical rotor,the rubbing frequency is higher,and then the rubbing frequency may be the main influence factor of the modal frequencies.These can also be obtained from Fig.7,in which we can see that the modal frequencies under high rotation speeds fluctuate and present uncertainty with the effects of the rubbing frequency,but at lower rotation speeds the modal frequencies with different rubbing frequencies are quite close.

The influence of contact time ratio is shown in Fig.8(b),and the constraint stiffness amplitude is 5×107N/m at that moment.The results indicate that contact time ratios have similar effects on the modal frequencies compared with the constraint stiffness amplitude.

To be noticed,Figs.17 and 18 in Ref.2 show that the modal frequencies under supercritical status increase monotonically with the increase of the constraint stiffness and contact time,which are different from the results in this paper.These results in Ref.2 are also listed in Appendix B in order to be compared with our calculation results conveniently.The mainly reason for the difference is that the modal truncation term j in Ref.2 is too small to reflect the influence of the time-varying features of the constraint stiffness adequately.Therefore,j should be given an enough large value so that we can reach the appropriate results.

Another parameter ‘average constraint stiffness” is defined to indicate the non-smooth constraint stiffness.Its value is the average of the non-smooth constraint stiffness and can be calculated by Eq.(11),and Fig.9 exhibits how the average constraint stiffness affects the modal frequencies for different values ofand α.

Fig.9 influence of average constraint stiffness on modal frequencies.

The two curves in Fig.9 are obtained while the rotor rotation speed λ is 0.6 and rubbing period Tkis T/2.The black curve represents the rubbing statuses with equal numbers of contact times and different constraint stiffness amplitude,and the red curve represents the rubbing statuses with equal constraint stiffness amplitude and different numbers of contact times.The figure shows that the modal frequencies are quite close for the two curves when the values ofare the same,which exhibits that if the rubbing frequencies were identical,there is similar influence of constraint stiffness on modal frequencies,no matter the case is ‘short contact time and large invasion” or ‘long contact time and small invasion”.

3.2.Stability characteristics

Stability characteristics are analyzed in this section when the fan of rotor is subject to non-smooth constraint.Due to the fact that the stability of the rotor system is mainly affected by the parametric excitation of the non-smooth constraint stiffness,so real parts of the eigenvalues under different rubbing frequencies are calculated,as seen in Fig.10.The constraint stiffness amplitudeand the contact time ratio α are given as 5×107N/m and 0.8,respectively.The following stability characteristics could be drawn from Fig.10(a):

(1)There exist more than one instable regions,including the normal modal instable region and the harmonic modal instable region.The normal modal instable region corresponds with the rubbing frequencies under which real parts related to normal mode are greater than 0,whereas harmonic modal instable region corresponds to the rubbing frequencies under which real parts of harmonic mode are greater than 033.For the given parameters,the real parts of the 2nd–4th harmonic modes are always lower than zero,which means that the instable regions of the 2nd–4th harmonic modes do not exist.Therefore,the harmonic modal instable regions in the figure correspond to the 1st harmonic frequency.Moreover,It should be noted that the normal instable region often exceeds the harmonic instable region.

(2)The eigenvalue real parts under different rotation speeds are almost coincident,which indicates that rotor stability is unrelated to the rotation speed.It seems that the rotor stability only depends on the non-smooth constraint stiffness parameters.

In general,the rubbing frequency primarily depends on the rotor rotation speeds and rubbing times in one rotation period.In order to learn the rotor stability with the influence of rubbing times under different rotation speeds,eigenvalue real parts under different numbers of rubbing times for several rotation speeds are derived through Fig.10(a),as shown in Fig.10(b).It can be concluded that at the low rotation speeds,the instability often occurs in the case of high rubbing times,while at high rotation speeds,that is just opposite.For example,we can see the instable start points for subcritical rotor(λ=0.6)and supercritical rotor(λ=1.4)are 2.1 and 0.9 times,respectively.In the practical rotating machinery,when the rotor operates at lower rotation speeds,rubbing times are also less generally.Therefore,it is rarely observed in the experiments that the instability of rubbing motion appears at the low rotation speeds.25

The influence of constraint stiffness parameters on the rotor stability is analyzed and Fig.11(a)shows effects of the constraint stiffness amplitude,where λ and α are selected as 1.4 and 0.8,respectively.It can be seen that the instability region is very small and the harmonic instability region even disappearswhen constraint stiffness amplitude is very low(1×107N/m).With the increase of the constraint stiffness amplitude,both the harmonic instability region and the normal instability region expand.Moreover,the rubbing times for the instability starting also increase,which implies that the instability phenomenon occurs under more rubbing times when the constraint stiffness amplitude improves.

Fig.11(b)suggests effects of the contact time ratio,where λ is still 1.4.The results show that both the instability regions and the rubbing times for the instability starting will increase when the contact time ratio becomes greater,which is similar to the influence of constraint stiffness amplitude.In fact,the rotor stability also mainly depends on the constraint extent,so that when either the constraint stiffness amplitude or the contact time ratio rises,the change laws of the rotor stability are almost similar.

Fig.10 Influence of rubbing frequency and rubbing times on stability of non-smooth constraint rotor.

Fig.11 Influence of constraint stiffness on stability of non-smooth constraint rotor.

4.Influence of non-smooth constraint on rotor response

From the conclusions in Section 3,we can infer that the response of rub-impact rotor must be changed due to the variation of modal frequencies and stability characteristics caused by non-smooth constraint.Up to present,researchers have investigated the vibration response of rub-impact rotor by experimental and theoretical methods.For example,Muszynska7and Abuzaid et al.29observed the vibration amplitude of rubbing rotor in the process of speed increase through experimental approach.Peletan34and Groll et al.35also studied the rotor response of rub-impact rotor using a simplified rotor model.In these studies,the amplitude jump phenomena and the change of resonance speeds were both obtained.This section will re-analyze the vibration response of rub-impact rotor and give an explanation from the view of modal characteristics obtained in previous section.

The rotor model in Refs.34,35,which is a simplified Jeffcott rotor,will be utilized in order to illustrate the influence of the non-smooth constraint on rotor response.The model and its governing equation can be seen in Appendix A.Fig.12 shows amplitude-rotation speed curves with the increase of the rotor rotation speeds.

The speed increasing process is 1–2–4–5 for no rub-impact rotor,while it changes into 1–2–3–5 when rub-impact occurs.The figure shows that the resonance speed and the resonance sideband of rub-impact rotor increase significantly in comparison to the case of no rub-impact condition.Generally,this is related to the stiffness increase due to rotor-to-stator rubimpact.So it could be explained by the theoretical results in the previous section.

First of all,rotor’s orbits and constraint stiffness at some rotation speed points are picked up from the simulation results,shown in Fig.13 and Table 1.The value for the constraint stiffness at certain time can be calculated through Eq.(12),where r0is the rotor-to-stator clearance,|q|is the rotor vibration amplitude obtained from rotor orbit,and kcis the stiffness of the stator.The rubbing frequency and contact time can also be obtained from the rotor’s orbit.

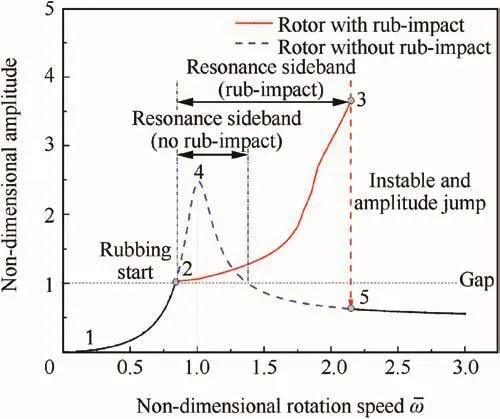
Fig.12 Comparison of non-dimensional amplitude between rotors with and without rub-impact.

The rotor orbits in Fig.13 imply that intermittent rubimpact occurs during the process of speed increase.Due to the fact that the alternative contact and separation of the rotor with stator,non-smooth constraint,which is time-varying,is applied to the rotor,modal frequencies increase as shown in Section 3.And along with the rise of rotor speeds,the nonsmooth constraint becomes stronger,which can be gotten from Fig.13 and Table 1 that the invasion depth and the average constraint stiffness increase.Consequently,modal frequencies of rotor system will continuously increase until the end of the rub-impact.Ultimately,the rotor vibrates with higher amplitude for a considerable speed range and exhibits as the increase of the resonance speed and the resonance sideband,shown in Fig.12.Furthermore,the expansion of resonance sideband may cause that rotor cannot pass the critical speed successfully,which will endanger safe operation of the rotor system.

Fig.13 Rotor axis orbits and constraint stiffness at different rotation speed ratios.

On the other hand,the amplitude jump phenomenon is also presented in Fig.12,which indicates the instability of the rotor motion.This phenomenon might also be related to the instability caused by the parametric excitation of the non-smooth con-straint stiffness.As can be seen,there exists the instable region because of the non-smooth constraint.When the rotor rotation speeds are lower,the constraint stiffness is weaker as well,then the instable region is also smaller and the rotor runs outside of the instable range.With the increase of rotor rotation speeds,the average constraint stiffness increases and the constraint extent becomes stronger(see Fig.13 and Table 1),and thus the instable regions,especially that with high rubbing frequencies,increase continuously.Until the case that rubbing frequencies are very close to or just at the instable region,the intermittent rub-impact becomes instable and amplitude jump phenomenon appears.

Table 1 Constraint stiffness at different rotor rotation speed ratios.

5.Experiments for rotor system with non-smooth constraint

5.1.Experiment system

5.1.1.Test devices

Fig.14 Overall view for overhung rotor-support test rig.

The experiment system mainly includes rotor system and rubimpact constraint device.The rotor has one disc installed overhung and two supports,as shown in Fig.14.The one near the disc is elastic support and the other is rigid support.A flexible coupling is connected between the motor and the shaft.The 1st critical speed of the rotor system is 4290 r/min,and corresponding mode shape is the shaft bending with pitch vibration at cantilever disc.The 2nd critical speed is 23,224 r/min and the corresponding mode shape is the bending between supports.The 2nd critical speed is not discussed here because the rotor operation speed is much lower than the 2nd critical speed.

The rub-impact constraint device is at the outside of disc,as shown in Fig.15.The rubbing ring is connected with the mounting pedestal and there is elastic material between them.We can change the constraint stiffness by replacing different elastic materials.The elastic material,mounting pedestal and rubbing ring are fixed together by a baf fle,and then the mounting pedestal is fixed to the foundation through a pull rod.In order to avoid direct contact of the rotor shaft with the rubbing ring to protect the rotor,a shaft sleeve is tight fitted with the rotor shaft.There exists clearance between the rubbing ring and the shaft sleeve,which is 0.5 mm in our experiment.The constraint effect is applied to the rotor through the contact of the rubbing ring and the shaft sleeve.

5.1.2.Measure points arrangement

Fig.16 shows the measure points arrangement of the experiment.Five eddy current displacement sensors are placed on the rotor(3300XL 5/8 mm made by Bently,sensitivity of 7.87 V/mm).Among them,1#measure point is as a tacho signal,which is used to obtain the rotation speeds.2#and 3#measure points are located at the position between the disc and elastic support to acquire the amplitudes in the horizontal and vertical directions.4#and 5#measure points are used to measure the horizontal and vertical vibration displacements of the rotor shaft sleeve when the constraint device is not mounted.When the constraint device is mounted to apply the constraint to rotor,4#and 5#measure points are used to measure the displacements of the rubbing ring.

Fig.15 Rub-impact constraint device.

Fig.16 Measure points for rotor.

5.2.Experimental results

5.2.1.Constraint effects of rub-impact

The unbalance of the rotor is 54.33 g·cm.During the accelerating process of rotation speed of rotor,vibration amplitude of rotor system will exceed the clearance between rotor and stator,then rub-impact occurs and constraint effects are applied to the rotor subsequently.Four different stiffness of rubbing rings are selected by the replacement of elastic materials to study the influence of different constraint conditions on rotor operation.The stiffness of the rubbing ring is measured based on the quasi-static experiment.The test rig is shown in Appendix C.The stiffness values obtained are 1.2×106N/m,1.95×106N/m,5.2×106N/m and 5×107N/m respectively,while their damping ratios are all approximately 0.13.

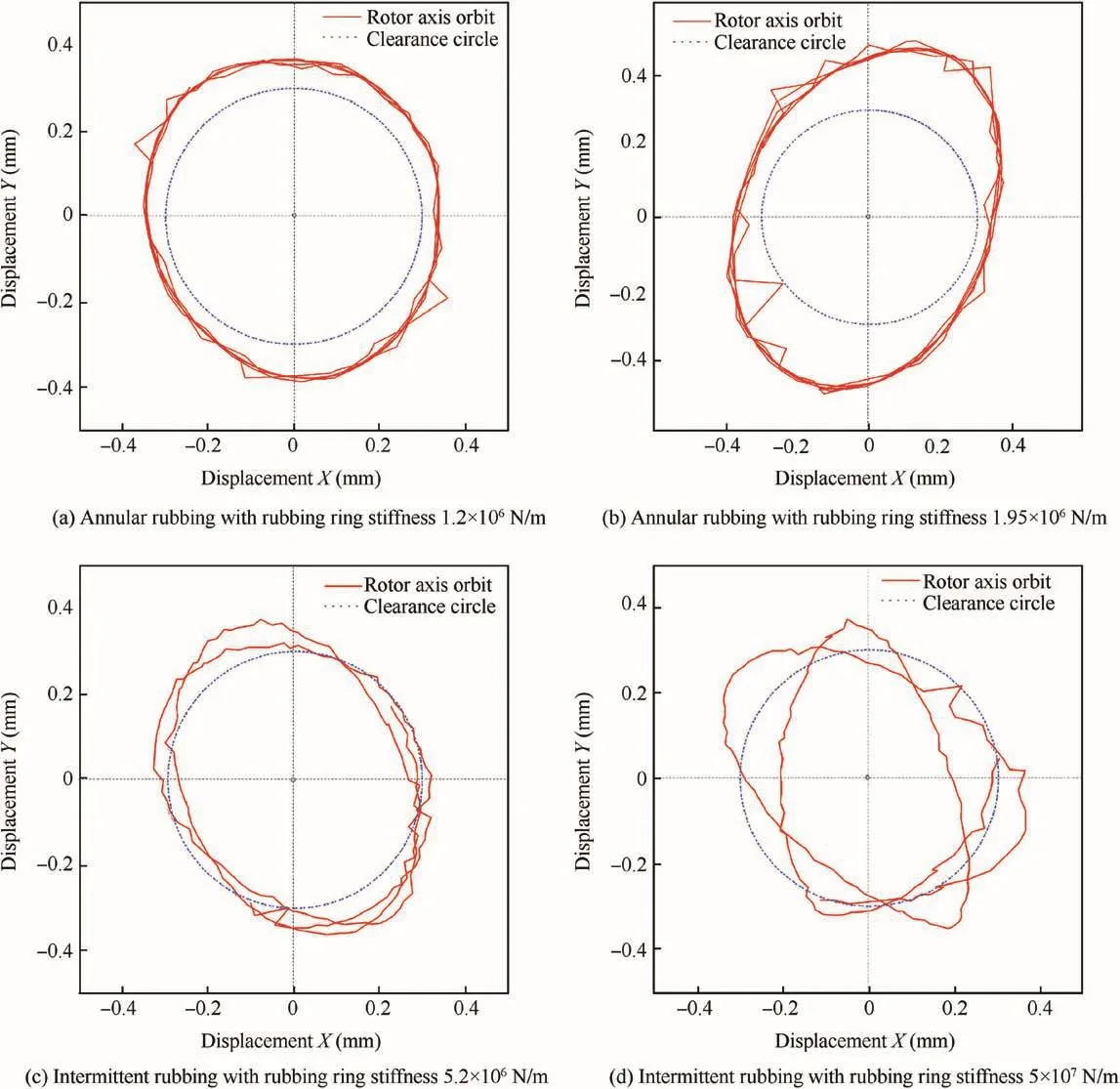
Fig.17 Rotor orbits measured for different rubbing states.

Fig.18 Constraint stiffness comparison for different stator stiffness.

The constraint conditions for different rubbing forms are distinct apparently and constraint stiffness values are estimated for the four rubbing states in Fig.17 according to the method in Section 4,as shown in Fig.18 and Table 2.It is noted that the rotor contacts the stator all the time and constraint stiffness is relatively constant with the rubbing ring stiffness being 1.2×106N/m and 1.95×106N/m,while the rotor contacts and separates with the stator repeatedly when the rubbing ring stiffness is 5.2×106N/m and 5×107N/m,respectively.At that time,the constraint stiffness varies between zero and a finite value,presenting significantly timevarying characteristics.In addition,it seems that the characteristics for constraint stiffness of the intermittent rub-impact obtained from experiment is basically consistent with that acquired from the simulation.

5.2.2.Influence of non-smooth constraint on rotor dynamic characteristics

The influence of the non-smooth constraint on the rotor modal characteristics will be analyzed in this section by amplituderotation speed curves,which can reflect the resonance speeds and stability characteristics of the rotor system.Fig.19 indicates the variation of the rotor vibration amplitude as rotor rotation speed rises for the four different rubbing ring stiffness.On the one hand,the experiment results show that the resonance speed and the resonance sideband increase in comparison to the case of no rubbing state,certainly caused by the constraint effect due to rub-impact.Besides,the higher the average constraint stiffness during rotor operation is,the stronger the constraint applied to rotor is.Consequently,the resonance speed and resonance sideband are also higher(see Fig.19 and Table 3).The above phenomena are coincident with the theoretical analyses.

Fig.19 Vibration amplitudes for rotor during rotation speed ascending for different constraint states.

On the other hand,the instability of rotor intermittent rubimpact could also be observed in the experiment.As we can see,in the case of no rub-impact or the annular rub-impact,there is no constraint effect or relatively constant constraint applied to the rotor,at that time the rotor motions are stable all the time and the amplitude-rotation speed curves are also similar.However,when the intermittent rub-impact occurs,the constraint effects applied to rotor are non-smooth and time-varying,and then we can see that the rotor’s motions are instable at a certain rotation speed point and the amplitude jump phenomena appear.Consequently,based on the results for the no constraint or the constant constraint and nonsmooth constraint conditions,we can infer that the non smooth constraint could lead to the instability of rotor motions,which also coincides with the theoretical analysis.

6.Conclusions

(1)The non-smooth constraint produced by the intermittent rub-impact will increase the modal frequencies and critical speeds of the rotor system significantly.Due to the time-varying features of the constraint stiffness,the modal frequencies for the intermittent rub-impact rotor present fluctuant changes with the increase of rotationspeed,which is different from the general linear rotor system,whose modal frequencies increase monotonically.The constraint amplitude and the contact time ratio have significant positive correlation in fluences on modal frequencies of the rotor system,especially at low rotation speed;however the rubbing frequency has little effect on the modal frequencies.

Table 2 Constraint stiffness parameters for different stator stiffness.

Table 3 Resonance speeds and stability characteristics for different constraint states.

(2)The non-smooth constraint is possible to lead to the rotor’s instability.The instable regions are mainly determined by the non-smooth constraint stiffness parameters,and the instable regions can expand significantly for the increase of average constraint stiffness,constraint amplitude and contact time ratio.

(3)The change of the rotor modal frequencies and stability characteristics due to non-smooth constraint could affect the rotor responses.Both the simulation and experiment results indicate that the non-smooth constraint could expand the resonance speed and resonance sideband of the rotor system,which sometimes may lead to the result that the rotor could not pass critical speed.Moreover,the non-smooth constraint may also increase the possibility of rotor instability.And once the instability happens,the amplitude jump appears immediately,during which the intermittent rub-impact vanishes suddenly and changes into the no rubbing state soon.

This paper has obtained the influence of the non-smooth constraint on the rotor modal characteristics theoretically,and the corresponding experimental results could also show the credibility of theoretical analysis.However,in the process of rotor rub-impact for the actual aero-engine,the constraint stiffness must change with the variation of rotor operation parameters,such as its rotation speeds,unbalance mass and other disturbance,showing the uncertainty characteristics.Therefore,some effective uncertainty analysis methods might be introduced.What’s more,non-smooth constraint may also affect the vibration response and cause the non-synchronous precession,leading to alternating stress and fatigue fracture of the rotor shaft.These problems should also be investigated in the future researches.

Acknowledgements

The authors would like to acknowledge the financial support from the National Natural Science Foundation of China(Nos.11772022,51575022 and 51475021).

Appendix A

Jeffcott rotor is always used to explain the mechanism of some vibration phenomena inrotordynamics because it is very simple but can cover the basic mechanical characteristics of the rotor system.In order to illustrate the influence of non smooth constraint on rotor response,the modified Jeffcott rotor which is shown in Fig.A1 is utilized in Section 4.The rotor has a massless shaft carrying a mid-span disk with mass m.The mass center of the rotor is located at a distance e from its geometrical center.The stiffness of shaft is k.The rotation speed of the rotor is ω.The stator has a rigid ring with mass neglected.The rigid ring is supported elastically,the stiffness of the support is kc,and the damping is ignored.The clearance between the rotor and the stator is r0.

Then the motion equation of the above rotor system can be written as

where q=x+iy,x is the horizontal displacement and y is the vertical displacement.vrelis the relative speed at the contact point of rotor,μ is friction coefficient,vrel=Ω|q|+ωrdisk,Ω is whirl angular velocity of the rotor,and rdiskis radius of the disk.

Eq.(A1)is rewritten in the following non-dimensional form to facilitate the analysis:

Fig.A1 Modified Jeffcott rotor model.

Table A1 Parameters of rotor.

The vibration amplitude could be calculated according to the above model using Newmark-β method,and the following parameters(see Table A1)are used for the simulation results in Section 4.

Appendix B

The influence of key parameters including amplitude of constraint stiffness and contact time on rotor’s modal frequency was reported in Ref.2,as shown in Figs.B1 and B2.The analytical method was similar to that described in Section 2.3 of this paper,but the number of modal truncation term j was chosen as 2 in the reference.The contact time ratio α=0.8,stiffness varying period Tk=0.5T,and the range of interval constraint stiffness kswas assumed to be [0, 4K1](K1=5×107N/m).The normal modal frequencies with different rotating speeds(λ=0.6, λ=0.8 at subcritical state and λ=1.2, λ=1.4 at supercritical state)are shown in Fig.B1.The results show that the frequencies at subcritical state and supercritical state increase with the amplitude of constraint stiffness.In Fig.B2,the stiffness varying period Tk=0.5T, the constraint stiffness amplitude ks=5×107N/m,and the contact time ratio is assumed to be[0,1].The results show that the frequencies increase with the contact time ratio.

Fig.B1 influence of constraint stiffness on modal frequency published in Fig.17 of Ref.2.

Fig.B2 Influence of contact time ratio on modal frequency published in Fig.18 of Ref.2.

Fig.C1 Quasi-static test rig of rubbing ring.

Appendix C

The stiffness of rubbing ring is obtained by the quasi-static experiment shown in Fig.C1.The Instron machine applies compression force to the rubbing ring through the double compression bars and loading shaft.The forces and displacements are measured by the force sensor and electrical micrometer gauge,respectively.Then the average stiffness is obtained according to the equation K=F/X.In the test,each rubbing ring is tested in 4 different directions and each direction is tested for 3 times.The final stiffness value used in the paper is the average value of all the measured results.

Appendix D.Supplementary material

Supplementary data associated with this article can be found,in the online version,at https://doi.org/10.1016/j.cja.2018.01.003.

1.Sinha SK.Non-linear dynamic response of a rotating radial Timoshenko beam with periodic pulse loading at the free-end.Int J Non Linear Mech 2005;40(1):113–49.

2.Wang C,Zhang DY,Ma YH,Liang ZC,Hong J.Theoretical and experimental investigation on the sudden unbalance and rubimpact in rotor system caused by blade off.Mech Syst Sig Process 2016;76:111–35.

3.Dai X,Zhang X,Jin X.The partial and full rubbing of a flywheel rotor–bearing–stop system.Int J Mech Sci 2001;43(2):505–19.

4.Choi YS.Dynamics of rotor rub in annular clearance with experimental evaluation.KSME J 1994;8(4):404–13.

5.Dai X,Dong J.Self-excited vibrations of a rigid rotor rubbing with the motion-limiting stop.Int J Mech Sci 2005;47(10):1542–60.

6.Fan CC,Pan MC.Active elimination of oil and dry whips in a rotating machine with an electromagnetic actuator.Int J Mech Sci 2011;53(2):126–34.

7.Muszynska A.Rotordynamics.New York:Taylor&Francis;2005.

8.Goldman P,Muszynska A.Rotor-to-stator,rub-related,thermal/mechanical effects in rotating machinery.Chaos,Solitons Fractals 1995;5(9):1579–601.

9.Sawicki JT,Montilla BA,Gosiewski Z.Thermomechanical behavior of rotor with rubbing.Int J Rotat Mach 2003;9(1):41–7.

10.Yong WT,Jian GY.Research on vibration induced by the coupled heat and force due to rotor-to-stator rub.J Vib Control 2011;17(4):549–66.

11.Beatty RF.Differentiating rotor response due to radial rubbing.J Vib Acoust 1985;107(2):151–60.

12.Choy FK,Padovan J,Li WH.Rub in high performance turbomachinery,modeling,solution methodology and signature analysis.Mech Syst Sig Process 1988;2(2):113–33.

13.Goldman P,Muszynska A.Chaotic behavior of rotor/stator systems with rubs.J Eng Gas Turb Power 1994;116(3):692–701.

14.Chu F,Zhang Z.Bifurcation and chaos in a rub-impact Jeffcott rotor system.J Sound Vib 1998;210(1):1–18.

15.Ma H,Shi CY,Han QK,Wen BC.Fixed-point rubbing fault characteristic analysis of a rotor system based on contact theory.Mech Syst Sig Process 2013;38(1):137–53.

16.Ma H,Wu ZY,Tai XY,Wen BC.Dynamic characteristics analysis of a rotor system with two types of limiters.Int J Mech Sci 2014;88:192–201.

17.Ma H,Zhao QB,Zhao XY,Han QK,Wen BC.Dynamic characteristics analysis of a rotor-stator system under different rubbing forms.Appl Math Model 2015;39(8):2392–408.

18.Jiang J,Ulbrich H.The physical reason and the analytical condition for the onset of dry whip in rotor-to-stator contact systems.J Vib Acoust 2005;127(6):594–603.

19.Black HF.Interaction of a whirling rotor with a vibrating stator across a clearance annulus.J Mech Eng Sci 1968;10(1):1–12.

20.Zhang W.Dynamic instability of multi-degree-of-freedom flexible rotor systems due to full annular rub.IMechE 1988;C252(88):305–8.

21.Childs DW,Kumar D.Dry-friction whip and whirl predictions for a rotor-stator model with rubbing contact at two locations.J Eng Gas Turb Power 2012;134(7):072502.

22.Ma Y,Cao C,Zhang D,Liang Z,Hong J.Constraint mechanical model and investigation for rub-impact in aero-engine system.ASME turbo expo 2015:turbine technical conference and exposition.2015 June 15–19;Montreal,Canada.New York:ASME;2015;V001T01A018.

23.Chu F,Lu W.Determination of the rubbing location in a multidisk rotor system by means of dynamic stiffness identification.J Sound Vib 2001;248(2):235–46.

24.Chu F,Lu W.Stiffening effect of the rotor during the rotor-tostator rub in a rotating machine.J Sound Vib 2007;308(3):758–66.

25.Zilli A,Williams RJ,Ewins DJ.Nonlinear dynamics of a simplified model of an overhung rotor subjected to intermittent annular rubs.J Eng Gas Turb Power 2015;137(6):065001.

26.Cao DQ,Chu SM,Li ZF,Liu RQ.Study on the non-smooth mechanical models and dynamics for space deployable mechanisms.Chin J Theoret Appl Mech 2013;45(1):3–15[Chinese].

27.Black HF.Forced subrotative speed dynamic action of rotating machines.J Mech Eng Sci 1968;10(4):1–12.

28.Childs DW.Rub-induced parametric excitation in rotors.J Mech Des 1979;101(4):640–4.

29.Abuzaid MA,Eleshaky ME,Zedan MG.Effect of partial rotorto-stator rub on shaft vibration.J Mech Sci Technol 2009;23(1):170–82.

30.Tai X,Ma H,Liu F,Liu Y,Wen B.Stability and steady-state response analysis of a single rub-impact rotor system.Arch Appl Mech 2015;85(1):133–48.

31.Liu S,Ma Y,Zhang D,Hong J.Studies on dynamic characteristics of the joint in the aero-engine rotor system.Mech Syst Sig Process 2012;29:120–36.

32.Chen G.Vibration modelling and verifications for whole aeroengine.J Sound Vib 2015;349:163–76.

33.Meng MW,Jun WJ,Zhi W.Frequency and stability analysis method of asymmetric anisotropic rotor-bearing system based on three-dimensional solid finite element method.J Eng Gas Turb Power 2015;137(10):102502.

34.Peletan L,Baguet S,Jacquet RG,Torkhani M.Use and limitations of the harmonic balance method for rub-impact phenomena in rotor-stator dynamics.ASME turbo expo 2012:turbine technical conference and exposition.2012 Jun 11–15;Copenhagen:Danemark.New York:ASME;2012:p.647–55.

35.Groll GV,Ewins DJ.On the dynamics of windmilling in aeroengines.Seventh international conference on vibrations in rotating machinery.2000 Sep 12–14;University of Nottinham,UK.London:Professional Engineering Publishing;2007.p.779–88.