Variations of flutter mechanism of a span-morphing wing involving rigid-body motions

Cho HUANG,Cho YANG,Zhigng WU,*,Chnghong TANG

aSchool of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China

bThe First Aircraft Institute,Aviation Industry Corporation of China,Xi’an 710089,China

1.Introduction

The morphing aircraft can be defined as aerial vehicles which are capable of altering their configurations actively to fulfill multiple missions.Previous surveys have shown that future aircraft with morphing wings gain superior flight performance.1,2As a solution of configuration transformation, the span-morphing wing has attracted aeronautical specialists’attention.The design and the test have been conducted on span-morphing wings to verify their feasibility.3,4However,many practical problems still remain and flutter instability is one of them.

Flutter is an aeroelastic problem which may destroy the aircraft in flight.Consequently,the flutter-free design is essential to aircraft safety.Specialists are required to master comprehensive knowledge about flutter mechanism,and such requirement in turn establishes challenges on flutter investigations for morphing aircraft.

The flutter investigations for morphing aircraft are mostly related to the Z-shape morphing wings,5–8while analyses and discussions on flutter characteristics with respect to the spanmorphing wing are quite rare in the aeroelastic literature.Recently,Huang and Qiu developed a state-space model to uncover the aeroelastic properties of a variable-span wing during the morphing process.9Almost at the same time,Zhang et al.derived nonlinear governing equations of motion for a deploying-and-retreating wing in supersonic flow.10

Generally, flutter is caused by the detrimental interaction between elastic structural dynamics and unsteady aerodynamics.The cantilever wing is usually studied first,which is the case in Refs.9,10.The conclusions made from the cantileverwing case,however,may be incorrect if rigid-body degrees of freedom are introduced to the structural dynamics.There is a potential threat caused by the coupling between rigid-body motions and wing elastic vibrations,and attention should be paid to this threat.11

Flutter induced by the preceding coupling is nowadays termed as Body-Freedom Flutter(BFF)where the rigid-body pitch motion mainly couples with the wing bending motion.12–14The BFF occurrence has been observed in the flutter analysis of a Z-shape morphing wing for an unrestrained aircraft.8Thus,the question how flutter mechanism of the span-morphing wing are affected by the rigid-body motions arises.To authors’best knowledge,no published effort has been devoted to answering such a question.

Focusing on a span-morphing wing model involving rigidbody motions,the present paper reveals the variations of its flutter mechanism from the classical Bending-Torsional Flutter(BTF)to the BFF,deepening the understanding of the aeroelastic properties of span-morphing wings.The rest part of the paper is organized as follows.Section 2 illustrates the schematic of the span-morphing wing model and states some assumptions to simplify the aeroelastic formulation.The development of equations of motion and the solution method are presented in Section 3.Section 4 gives the numerical results and Section 5 demonstrates the influence of some parameters on the variations of flutter mechanism,which is followed by the final conclusions drawn in Section 6.

2.Preliminaries

The investigated span-morphing wing is illustrated in Fig.1.Fig.1(a)displays its three-dimensional configuration.The semispan model perturbs around a trimmed state.Only two symmetric rigid-body motions,i.e.the pitch motion θ and the plunge motion w,are allowed.The main structure is a telescopic spar similar to the one in Ref.3.The spar provides most weight and rigidity,and it is comprised of two thin-walled tubes where the inner tube moves freely inside the outer one.Thus,a rectilinear Elastic Axis(EA)is assumed.It runs from the inboard to the outboard,indicating that the wing has a medium or high aspect ratio.

The origin of the rectangular coordinate system is placed at the intersection of the EA and the wing-root section.The y axis coincides with the EA and the z axis points to the downward.Fig.1(b)displays the planform dimensions.A concentrated mass MFwhich lies ahead of the origin XFrepresents the inertia of the half fuselage.A tip weight representing the winglet is added,and the same idealization is applied to the tip weight MPlocated at the intersection of the EA and the wing-tip section.Besides,the following simplifications for the wing are made:

(1)The chord-wise sections perpendicular to the EA are absolutely stiff,and its length is constant.

(2)The span lengths of two tubes are identical,and the length is l0for the completely retracted configuration,and thus 2 l0for the fully extended configuration.

(3)The wing is treated as a three-segment stepped Euler-Bernoulli beam during the span morphing,and the location of the EA,the static unbalance Xαas well as the radius of gyration Rαare all assumed unchanged along the span.

(4)The in-plane deformation is neglected.

(5)The span-morphing speed is so slow that any change about inertia and stiffness stemmed from such speed is ignored in the present quasi-static modeling.

3.Equations of motion and solution methods

Based on the aforementioned definition,the kinematics of the fuselage is described by the plunge motion w,positive downward,and the pitch motion θ,positive nose-up.The kinematics of the wing is represented by the EA motion.The EA motion which is commonly described by a vertical translation,h,positive downward,and a twist about the EA,α,positive nose-up,can be further decomposed into the rigid-body components and the elastic components as follows:

Fig.1 Schematic of a span-morphing wing model.

where Λ,ψ and φ denote the sweep angle,the bending displacementandthetorsionaldisplacement,respectively.Consequently,thekinematicsofthetipweightisgivenbythemotionshandαat the location y=l.In Eq.(1),the elastic displacements ψ and φ are usually expressed in modal expansion forms:

In the morphing process,the ith mode shapes fi(y)and gi(y)are piecewise functions defined in three length intervals,[0,l-l0],[l-l0,l0]and[l0,l],and ψi(t)and φi(t)are the corresponding modal coordinates.Using the analytical method proposed in Ref.15,the uncoupled natural bending and torsional modes of the three-segment stepped cantilever beam are chosen.Herein the number of the modes,nψ=2 and nφ=1,are adopted.

The kinetic energies of the fuselage,the wing and the tip weight are given respectively in the following compact forms:

where m denotes the wing mass per unit length,RFthe radius of gyration of the fuselage about the origin,and RPthe radius of gyration of the tip weight about the EA.The wing length at any instance is l,and its value falls in the interval between l0and 2l0.

The potential energy is attributable to the strain energy of the wing that reads:

where E(y)I(y)and G(y)J(y)are local bending rigidity and torsional rigidity,respectively.

The aerodynamic strip theory is applied to the wing immersed in an incompressible airstream.Utilizing Theodorsen’s unsteady thin-airfoil theory,the running lift L and moment Mincluding the sweep effect are simplified as

where the aerodynamic terms Lnc,Lc,Mncand Mccan be found in Ref.16,and subscripts ‘nc” and ‘c” represent noncirculation and circulation,respectively.Three modifications in the above equations are addressed.Firstly,the Theodorsen function C(k)is approximated by a finite-state rational function obtained from Ref.17:

where i denotes the imaginary unit,k=(ωb)/(VcosΛ)is the reduced frequency,and ω,b and V are the circular frequency,the semi-chord length and the airstream speed,respectively.Secondly,the local lift-curve slope CLαtakes place of the coefficient 2π in those aerodynamic terms in Eq.(5)and CLαincluding the effect of the finite span is used as18

where AR=l/b denotes the aspect ratio and a0=2π is employed here for simplicity.The coefficient CLαcan also be replaced by simulated CFD data or wind-tunnel data.Finally,the aerodynamics on both the winglet and the fuselage are neglected since it is hard to acquire their analytical expressions.Substituting foregoing expressions into the Lagrange’s equation,the aeroelastic equations of motion are ultimately developed in a state-space form:

where the vector X contains the states corresponding to the kinematic components in Eq.(1),their derivatives with respect to time as well as the aerodynamic lags.The state matrix Γ is expressed as

where M stands for the structural inertial matrix,K the structural stiffness matrix,Q2the aerodynamic inertial matrix,Q1the aerodynamic damping matrix and Q0the aerodynamic stiffness matrix.The parameter vnequals(VcosΛ)/b,and the matrices A,B and C which are associated with Eq.(9)are given as follows:

Finally,the flutter solution turns to be an eigenvalue problem of Eq.(10)for a specific range of airstream speeds.The flutter onset mathematically refers to a condition where the real part of one eigenvalue becomes zero while its associated imaginary part remains a nonzero value.Using eigenvalue decomposition function and other plotting syntax in MATLAB software,the flutter speed and frequency can be quickly captured from a V-g-f diagram.It should be noted that the state-space solution mentioned above,rather than the traditional frequency-dependent solution,is beneficial to the BFF investigation where the predominant eigenvalues lying in the proximity of the origin of the complex plane can be effectively solved.19

4.Numerical example

The data used in the present span-morphing wing model example are summarized in Table 1.These data are chosen to re flect a possible wind-tunnel flutter test model.Also the following piecewise relationship for the three-segment stepped beam is established due to the assumption that the two tubes of the wing spar share the same properties concerning the rigidity and the mass per unit length:

In Eq.(11),the subscript ‘Ref” refers to the completely retracted configuration.According to Table 1,the aspect ratio for the completely retracted configuration is 5,and becomes 10 when the wing is fully extended.

Fig.2 shows the variations of span-morphing location on the flutter characteristics of the model.The dimensionless flutter speed vFlutter=V/ωRefb and frequency ΩFlutter= ω/ωRefare used and vary with the dimensionless length ratio χ.Also calculated are the flutter speeds and frequencies in the cases where the rigid-body degrees of freedom and the elastic torsional degree of freedom are excluded successively.

As anticipated,a continued decrease in the flutter speed accompanying the increase in span length is observed.However,the flutter speeds disagree with the calculated ones in the degrees-of-freedom-excluded cases.When the wing extends,it is found that the flutter speed approaches the value in the torsional-degrees-of-freedom-excluded case.Moreover,there is an abrupt drop of the flutter frequency in the interval between χ =1.4 and χ =1.5.When χ is less than 1.4,the flutter frequency lies between the frequencies of the first bending mode and the first torsional mode.If χ is beyond 1.5,the flutter frequency falls in the frequency band corresponding to the rigid-body pitch motion.

To explain the preceding frequency drop,the V-g-f diagrams for χ =1.0 and χ =2.0 are then plotted and displayed in Fig.3 and Fig.4 respectively.Clearly,the completely retracted configuration of the span-morphing wing exhibits classical BTF where the torsional mode mainly couples with the second flexural mode and eventually goes unstable.On the contrary,the rigid-body pitch mode couples with the first bending mode when the wing is fully extended,leading tothe BFF.The BTF still exists but occurs at a higher airstream speed.

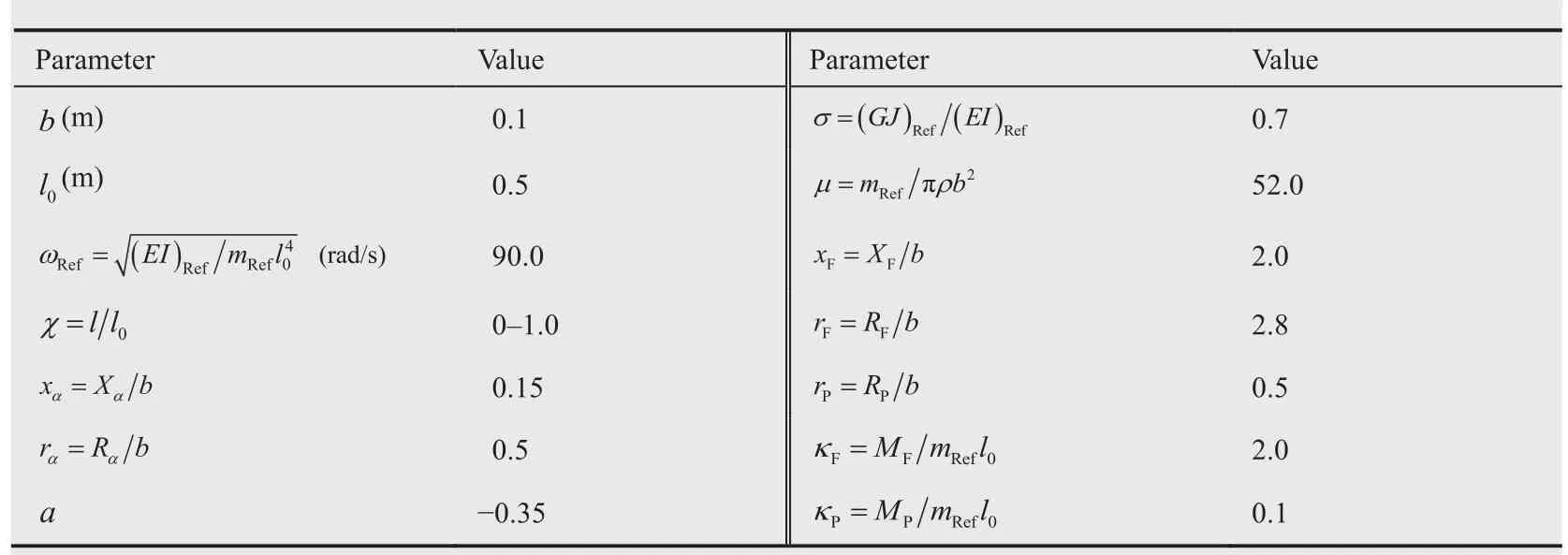
Table 1 Data for present span-morphing wing model.

Fig.2 Effects of variation of span-morphing location on flutter characteristics.

Fig.3 V-g-f diagram of span-morphing wing model when χ=1.0.

Fig.4 V-g-f diagram of span-morphing wing model when χ=2.0.

Another calculation for the case with all bending modes excluded is also carried out,and no flutter instability is found.Since the frequency of the torsional mode is much higher compared to the one of the rigid-body pitch mode,the abrupt drop of the flutter frequency indicated in Fig.2 then reveals a variation of flutter mechanism,i.e.,from the BTF to the BFF.The rigid-body pitch mode and the torsional mode dominate the flutter mechanism for different span-morphing stages.Also,the fact that neither of these two modes should be excluded in the present example is demonstrated by Fig.2.

Fig.5 Effect of wing mass ratio on variation of flutter mechanism.

It should be noted that the flutter mode in the present BFF mechanism is always the pitch mode.Although the bending mode often acts as the stability killer in the current BFF investigations,the situation where the pitch mode becomes unstable can also be discovered in the early BFF literature.12,13,20–22Whether the pitch mode or the bending mode goes unstable is strongly dependent on the parameter selection.

5.Influence of some parameter variations

The effect of the wing mass ratio μ is illustrated in Fig.5.It can be seen that a small value of μ makes the transition of the flutter mechanism appear at the early stage of the span morphing.This implies that the lightweight wing is usually susceptible to the BFF.The effect of μ on the BFF speed,however,is not so significant in the present example.The BFF speed falls in the vicinity of a limited value when the wing approaches its fully extended configuration.On the other hand,the decrease of μ is destabilizing for the BTF.

Fig.6 Effect of sweep angle on variation of flutter mechanism.

Fig.8 Effect of location of fuselage mass on variation of flutter mechanism.

Fig.9 Effect of radius of gyration of fuselage on variation of flutter mechanism.

Fig.10 Effect of tip mass on variation of flutter mechanism.

The effect of the sweep angle Λ is shown in Fig.6.Apparently,Λ decreases the BTF speed but makes no considerable influence on the change of its frequency.Because the change of Λ leads to the change of the inertia and the aerodynamics at the same time,the corresponding transition from the BTF to the BFF is a little complex.For Λ less than 5°,the transition still occurs within χ∈[1.4,1.5],and the BFF speed is slightly increased by the increase in Λ.For a certain value of Λ in the range between 5°and 10°,the preceding transition is delayed and makes the trend of the BFF speed irregular.

The results displayed in Fig.7 reveal that the increase of the fuselage mass expedites the transition of the flutter mechanisms if the wing total mass remains constant.Furthermore,a heavier fuselage leads to a lower BFF speed and frequency,whereas it has an opposite and extremely limited influence on the BTF.Fig.8 depicts the variation of the flutter characteristics when the effect of the location of the fuselage mass xFis studied.The increase of xFplays a stabilizing role on the BFF,and its effect on the BTF is negligible.The BFF occurrence would be eliminated if xFcontinues to increase.For the present span-morphing wing model,it can be inferred that a certain large value of xFcan make the flutter characteristics almost identical to the one of the cantilever wing.

Fig.9 presents the effects of the radius of gyration of the fuselage rF,cgon the flutter characteristics for some specified morphing locations.Here the parameter rF,cgis defined by

The increase in rF,cgto suppress the BFF seems to be more effective than the enlargement of xF.Since the BTF is mostly related to the properties of the wing alone,the effect of rF,cgon the BTF is not noticeable as expected.This suggests that an unrestrained aircraft with large pitch moment of inertia contributed mainly from the fuselage is not sensitive to the BFF.As a result,the flutter mechanism may vary little if more sophisticated methods such as those proposed in Refs.9,10are applied to the span-morphing wing model.

The results in Fig.10 indicate that an increase of the tip mass can reduce the flutter speed and frequency for both the BTF and the BFF.In the present analysis,the transition of the flutter mechanism which occurs within χ∈ [1.4,1.5]is still observed regardless of any change of the tip mass.

6.Conclusions

(1)In this paper,an aeroelastic span-morphing wing model involving the rigid-body motions is developed in a quasistatic way.The flutter characteristics of such a model is analyzed,and the results reveal variations of flutter mechanism from the BTF to the BFF accompanying the fact that the flutter speed decreases ceaselessly as the span increases.For an unrestrained aircraft having a symmetric configuration and a span-morphing wing,it is suggested that the rigid-body motions especially the pitch motion should be included in the flutter analysis to obtain more accurate understanding of its flutter characteristics.

(2)Effects of some parameters belonging to the wing,the fuselage and the tip weight on the variation of flutter mechanism are investigated respectively.As for the flutter speed and the transition of flutter mechanism,the variation of either or both is observed.The parameters of the fuselage have limited in fluences on the BTF but significant effects on the BFF.A fuselage with a large value of the radius of gyration about the wing’s elastic axis eliminatesthe BFF occurrenceof thespanmorphing wing most effectively.

1.Barbarino S,Bilgen O,Ajaj RM,Friswell MI,Inman DJ.A review of morphing aircraft.J Intel Mat Syst Str 2011;22(9):823–77.

2.Weisshaar TA.Morphing aircraft systems:historical perspectives and future challenges.J Aircraft 2013;50(2):337–53.

3.Blondeau J,Pines D.Design and testing of a pneumatic telescopic wing for unmanned aerial vehicles.J Aircraft 2007;44(4):1088–99.

4.Vocke RD,Kothera CS,Woods BKS,Wereley NM.Development and testing of a span-extending morphing wing.J Intel Mat Syst Str 2011;22(9):879–90.

5.Tang D,Dowell EH.Theoretical and experimental aeroelastic study for folding wing structures.J Aircraft 2008;45(4):1136–47.

6.Liska S,Dowell EH.Continuum aeroelastic model for a foldingwing configuration.AIAA J 2009;47(10):2350–8.

7.Wang I,Gibbs SC,Dowell EH.Aeroelastic model of multisegmented folding wings:Theory and experiment.J Aircraft 2012;49(3):911–21.

8.Snyder MP,Sanders B,Eastep FE,Frank GJ.Vibration and flutter characteristics of a folding wing.J Aircraft 2009;46(3):791–9.

9.Huang R,Qiu ZP.Transient aeroelastic responses and flutter analysis of a variable-span wing during the morphing process.Chinese J Aeronaut 2013;26(6):1430–8.

10.Zhang W,Sun L,Yang XD,Jia P.Nonlinear dynamic behaviors of a deploying-and-retreating wing with varying velocity.J Sound Vib 2013;332(25):6785–97.

11.Wu ZG,Yang C.Flight loads and dynamics of flexible air vehicles.Chinese J Aeronaut 2004;17(1):17–22.

12.Widmayer E.Some low-speed studies of the effects of wing location on wing-deformation-body-freedom flutter.Langley Field:Langley Aeronautical Laboratory,National Advisory Committee for Aeronautics;1952.Report No.:RM-L52I24.

13.Weisshaar TA,Zeiler TA.Dynamic stability of flexible forward swept wing aircraft.J Aircraft 1983;20(12):1014–20.

14.Love MH,Zink PS,Wieselmann PA,Youngren H.Body freedom flutter of high aspect flying wings.46th AIAA/ASME/ASCE/AHS/ASC structures,structural dynamics&materials conference;2005 Apr 18–21;Austin,USA.Reston:AIAA;2005.

15.Naguleswaran S.Vibration of an Euler-Bernoulli beam on elastic end supports and with up to three step changes in cross-section.Int J Mech Sci 2002;44(12):2541–55.

16.Bisplinghoff RL,Ashley H,Halfman RL.Aeroelasticity.New York:Dover Publications;1996.p.398.

17.Venkatesan C,Friedmann P.New approach to finite-state modeling of unsteady aerodynamics.AIAA J 1986;24(12):1889–97.

18.Diederich FW.A planform parameter for correlating certain aerodynamic characteristics of swept wings.Langley Field:Langley Aeronautical Laboratory,National Advisory Committee for Aeronautics;1951.Report No.:TN-2335.

19.Pototzky AS.Modeling state-space aeroelastic systems using a simple matrix polynomial approach for the unsteady aerodynamics.NATO RTO specialists meeting AVT-154 on advanced methods in aeroelasticity;2008 May 5-7;Loen,Norway.Brussels:NATO Science and Technology Organization;2008.

20.Pak CG,Truong S.Creating a test-validated finite-element model of the X-56A aircraft structure.J Aircraft 2015;52(5):1044–67.

21.Schmidt DK.MATLAB-based flight-dynamics and flutter modeling of a flexible flying-wing research drone.J Aircraft 2016;53(4):1045–55.

22.Cunningham HJ,Lundstrom RR.Description and analysis of a rocket-vehicle experiment on flutter involving wing deformation and body motions.Langley Field:Langley Aeronautical Laboratory,National Advisory Committee for Aeronautics;1955.Report No.:TN-3311.