超高维数据的稳健秩条件特征筛选

李向杰，张景肖

(中国人民大学a.应用统计科学研究中心；b.统计学院，北京 100872)

一、引 言

随着社会的进步和科技的发展，高维和超高维数据在生活中越来越普遍。对于高维数据，正则化回归技术在最近20年来已经很成熟，例如LASSO、 SCAD、MCP、Adaptive -LASSO、Elastic net、Dantzig Selector等。但是，在超高维数据情况下，因为变量维度p以样本量n的指数阶增加，直接应用上述的正则化方法会产生算法不稳定、推断不正确、计算成本高等一系列问题，因此超高维特征筛选方法应运而生。

超高维特征筛选方法是将维度从非常大的p降到适中的d，然后再用上述提到的LASSO等正则化方法进一步进行分析。超高维筛选方法可以分成两类：第一类是基于特定模型的筛选方法，例如Fan等在线性模型的框架下提出的SIS方法和迭代的SIS方法(ISIS)[1]；Hall等提出的基于广义相关系数的gcorr筛选方法[2]；Liu等针对超高维变系数模型提出的条件相关系数筛选方法(CCSIS)[3]。此外，还有MMLE[4]、RRCS[5]、NIS[6]、GSIS[7]等；第二类是模型自由 (Model Free)的筛选方法，如F-KOL[8]、SIRS[9]、 DCSIS[10]、MVSIS[11]、HDSIS[12]。Liu等对超高维筛选方法做了较为全面的文献综述[13]。

Barut等在2016年首次提出了条件边际筛选(Conditional SIS)方法，在线性模型的假设下，当条件变量是空集时，条件SIS就变成了SIS，但该方法只对广义线性模型适用，并且对异常值不够稳健[14]。Wang等提出了条件独立筛选方法MCSCIS，虽然它不依赖于模型设定,但是由于它需要二维的经验分布函数来估计联合分布，在小样本情况下表现不是很好[15]。本文提出了一种新的条件筛选方法——稳健秩条件筛选方法(RRCSIS)，该方法在因变量或者自变量含有厚尾分布或者含有异常值时表现都很稳健，并且可以衡量一般的相关性，还可以刻画条件相关性，另外该方法也是模型自由的。

二、研究方法

皮尔逊相关系数度量的是线性相关性，当数据之间存在非线性关系或者有异常值时，皮尔逊相关系数不再适用。在Anscombe的4组数据(R软件中，直接输入变量Anscombe可查到)中，每组数据中的x和y的皮尔逊相关系数都为0.816,但是它们呈现出不同的关系，如图1所示。

图1　4个Anscombe 数据集的线性回归图

从图1可以看出，数据1(左上图)可以很好地用线性回归模型来拟合，数据3(左下图)除一个异常点外也有比较清楚的线性关系，而数据2(右上图)则呈现出明显的非线性关系，数据4(右下图)相关性很弱。这4个数据集的Kendallτ相关系数分别为0.636，0.564，0.964，0.420，而用本文中给出的基于条件稳健秩的相关性度量，这4个数据集之间的相关性程度分别为0.818，0.691，0.991，0.200，由此可以看出，相比皮尔逊相关系数和Kendallτ相关系数，本文提出的度量表现得更为合理。

(一)基于条件稳健秩的相关性度量

令Y是因变量，X=(X1，X2，…，Xp)T是p维的自变量，Z是条件变量，假设{(Xi，Yi，Zi)，i=1，2，…，n}是来自总体(X，Y，Z)的n个随机样本，Xij是第j个变量的第i个样本，i=1,2，…,n；j=1,2，…，p。定义Fz=(Z≤z)，Fy=(Y≤y)，Fy|z=(Y≤y|Z≤z)，为了衡量在给定条件变量Z下因变量Y和自变量Xj的关系，本文用Xj的秩来构造相关性度量，j=1，2，…，p。令表示随机样本Xij的秩。明显地，R(Xij)服从离散均匀分布，其分布为(R(Xij))=1/n，i=1，2，…，n，从而可以得到R(Xij)的期望为E[R(Xij)]=(n+1)/2，为此可以构造如下的条件稳健秩相关度量统计量：

wj=EXj，Y，Z{[R(Xj)-E(R(Xj))]FY|Z}

(1)

其中期望是对Xj,Y,Z同时来计算。 值得注意的是，如果当条件变量Z为空时，该方法很自然可以表示为wj=EXj，Y{[R(Xj)-E(R(Xj))]FY}，因此它可以同时处理条件特征筛选和特征筛选。

(二)样本估计

令估计量：

(2)

(3)

(4)

(a)Y=κ·X+ε

(b)Y=κ·exp(X·I(X<0))+ε

图2　模型(a)中的箱线图

图3　模型(b)中的箱线图

图4　不同筛选方法随着样本增加的时耗变化图

三、条件确保筛选过程

根据式(4)提出的新的条件筛选方法RRCSIS，采用Zhu等人采用的记号[9-10]，在给定Z的条件下，定义解释变量X中对Y重要的变量集合为：

A={j：存在某y∈RY|Z,使得FY|x,Z依赖Xj，

j=1，2，…，p}

其中RY|Z是给定随机变量Z下Y的支撑，重要变量构成的集合A简称活跃集，并定义J={1，2，…，p}A为非活跃集。给定一个阈值d，用下式来估计A：

一方面，本文提出的RRCSIS方法没有对模型设定做假设，即它是“Model Free”的；另一方面，由于估计量只依赖于经验分布函数和秩排序，故它对厚尾分布或者异常值数据都比较稳健，并且对原始数据的严格单调变换是保持不变的。

此外，类似迭代的SIS[1]、迭代的SIRS[9]和迭代的DCSIS[16]，本文提出了迭代的RRCSIS，简称为IRRCSIS，过程如下：

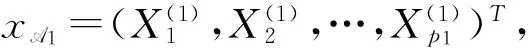
第三步：更新A1∶=A1∪A2，并重复第二步，直到总的筛选变量个数达到预选的d，最终筛选的变量集合为A1。

四、数值模拟

下面通过数值模拟来检验RRCSIS的表现，并且和已有的 SIS[1]、SIRS[9]、DCSIS[10]和MCSCIS[15]等重要方法进行对比，取d=[n/log(n)]。采用以下3条准则进行对比：

1.Pj：给定一个阈值d，在多次模拟中真变量Xj被选中的比例。Pj越大说明筛选的效果越好，反之越差。

2.Pall：给定一个阈值d，在多次模拟中所有真变量都被选中的比例。Pall越大说明筛选的效果越好，反之越差。

3.MMS：包含所有真实变量所需要的最少的变量个数。

例1(线性模型) 本例采用了Wang 等的例1[15]，即数据由下面的线性模型产生：

Y=XTβ+ε

表1和表2分别给出了例1在ρ=0.5和0.8时的筛选结果，在d=[100/log (100)]=21的情况下，无论是从包含真实变量的比例还是从最小模型数MMS来看，RRCSIS都有最优的表现。当误差项为标准正态分布时，由于此时误差项没有异常值，所有的筛选方法都不错，但是在误差项含有异常值或者是厚尾分布时，SIS、DCSIS就几乎失效，SIRS和MCSCIS也受到很大的影响，而RRCSIS表现很稳健。

表1　例1(线性模型) 在ρ=0.5下的Pj，Pall以及MMS的均值和标准差(括号内)

例2(变系数模型) 考虑如下变系数模型：

Y=β1(Z)X1+β2(Z)X2+β3(Z)X3+β4(Z)X4+ε其中β1(Z)=2，β2(Z)=3Z,β3(Z)=(Z+1)2，β4(Z)=4sin(2πZ)/(2-sin(2πZ))，即活跃集是A={1,2,3,4}。解释变量X=(X1，X2，…，Xp)T服从多元t分布T(0p，Σ,v)，其中Σ=(σij)p×p是协方差矩阵，σij=ρ|i-j|,i,j=1,2，…,p,v表示多元t分布的自由度，0p是p维零向量。条件变量Z服从均匀分布U(0，1)。本例取样本量n=200、p=1 000并取ρ=0.5和0.8两种情况，误差的分布和例1一样，每种情况模拟300次。表3和表4分别给出了在ρ=0.5和ρ=0.8下的筛选结果，这是因为在生成自变量和因变量Y时都含有大量的异常值，而SIS、DCSIS方法对含有异常值的数据不稳健；SIRS虽然对Y含有异常值时比较稳健，但是此例中X也含有大量的异常值，所以SIRS表现也不佳；相反RRCSIS和MCSCIS的表现很稳健，能够准确地筛选出重要变量。

表2　例1(线性模型) 在ρ=0.8下的Pj，Pall以及MMS的均值和标准差(括号内)

表3　例2(变系数模型) 在ρ=0.5下的Pj，Pall以及MMS的均值和标准差(括号内)

表4　例2(变系数模型) 在ρ=0.8下的Pj，Pall以及MMS的均值和标准差(括号内)

例3本例是为了显示出迭代的RRCSIS方法能有效地筛选边际不相关但联合相关的重要变量。考虑如下3个模型：

表5　例3中3个模型RRCSIS方法和迭代的RRCSIS方法的比较

五、实证分析

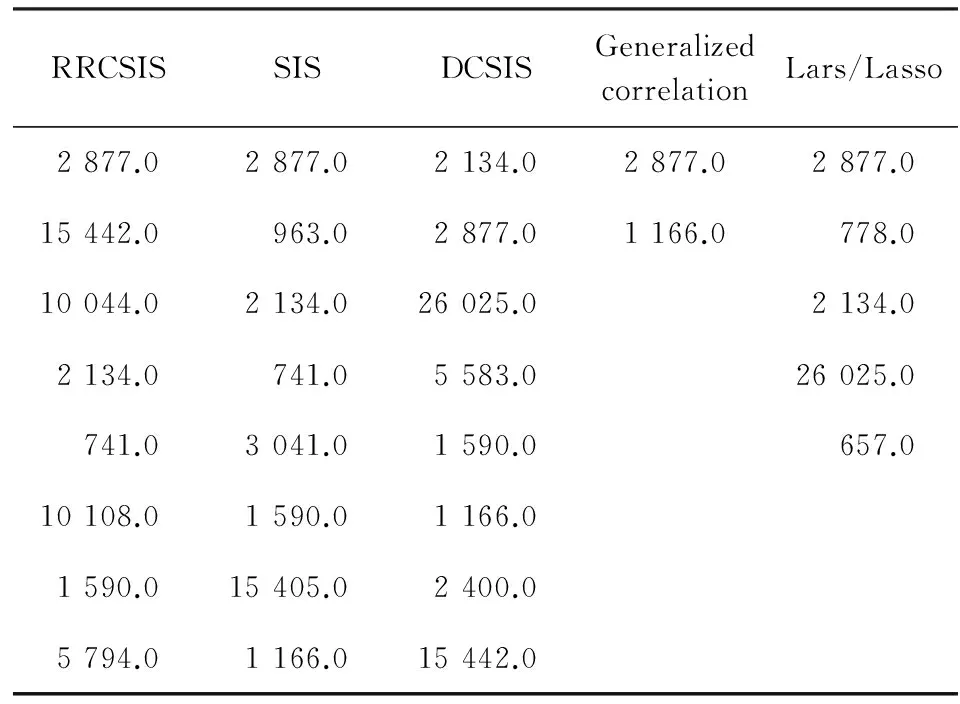
下面将RRCSIS方法应用到实际数据分析中。该数据是研究小鼠的基因对G蛋白耦联受体(G Protein-coupled Receptor)(Rol)的影响，因为此蛋白耦联受体与扩张心肌病有很强相关关系，故该数据实际上是研究小鼠基因对扩张心肌病的影响。该数据集曾被Hall 等研究过[2，10，17]。此数据有30个样本(n=30)，6 319个基因(p=6 319)，因变量是 Rol。图5给出了因变量的直方图，可以看出该数据是右偏的并且有潜在的异常值，此数据特征使我们可以应用RRCSIS来分析该数据。表6给出了在d=8下不同方法的基因筛选结果，可以看出RRCSIS可以很好地筛选出重要的基因Msa.2134.0 和 Msa.2877.0，并且筛选出的其他基因和已有方法(如DC-SIS)筛选的基因有很多重合， Li等已经验证了DC-SIS的合理性[10]，这也验证了RRCSIS在无条件变量下筛选的合理性。

图5　Rol的直方图

RRCSISSISDCSISGeneralizedcorrelationLars/Lasso2877.02877.02134.02877.02877.015442.0963.02877.01166.0778.010044.02134.026025.02134.02134.0741.05583.026025.0741.03041.01590.0657.010108.01590.01166.01590.015405.02400.05794.01166.015442.0

六、结论与展望

本文提出了一种新的特征筛选方法RRCSIS，该方法不仅可以应用条件特征筛选，还可以应用于普通的特征筛选。为了识别那些对因变量边际不相关但联合相关的情况，本文还提出了迭代的稳健秩特征筛选，即IRRCSIS。模拟结果显示该方法具有较好的稳健性，并且是模型自由的，实际数据分析结果显示该方法有效。由于该方法不依赖于模型设定，并且对异常值很稳健，所以其应用并不仅仅局限在生物信息领域。此外，当样本量充分大时，还可以考虑多维的因变量以及多维的条件变量，对应FY|Z=(Y1≤y1,…,Yq≤yq|Z1≤z1,…,Zm≤zm)可以用相应的多维的示性函数来估计。

参考文献：

[1]Fan J，Lv J.Sure Independence Screening for Ultrahigh Dimensional Feature Space[J].Journal of the Royal Statistical Society，Ser.B，2008,70(5).

[2]Hall P，Miller H.Using Generalized Correlation to Effect Variable Selection in very High Dimensional Problems[J].Journal of Computational and Graphical Statistics，2009,18(3).

[3]Liu J，Li R，Wu R.Feature Selection for Varying Coefficient Models with Ultrahigh-Dimensional Covariates[J].Journal of the American Statistical Association，2014,109(505).

[4]Fan J，Song R.Sure Independence Screening in Generalized Linear Models with NP Dimensionality[J].The Annals of Statistics，2010,38(6).

[5]Li G，Peng H，Zhang J，Zhu L.Robust Rank Correlation Based Screening[J].The Annals of Statistics，2012,40(3).

[6]Fan J，Ma Y，Dai W.Nonparametric Independence Screening in Sparse Ultrahigh-Dimensional Varying Coefficient Models[J].Journal of the American Statistical Association，2014,109(507).

[7]马学俊.GSIS 超高维变量选择[J].统计与信息论坛，2015，30(8).

[8]Mai Q，Zou H.The Fused Kolmogorov Filter：A Nonparametric Model-free Screening Method[J].The Annals of Statistics，2015,43(4).

[9]Zhu L，Li L，Li R，Zhu L.Model-free Feature Screening for Ultrahigh Dimensional Data[J].Journal of the American Statistical Association，2011,106(496).

[10] Li R，Zhong W，Zhu L.Feature Screening via Distance Correlation Learning[J].Journal of the American Statistical Association，2012,107(499).

[11] Cui H，Li R，Zhong W.Model-free Feature Screening for Ultrahigh Dimensional Discriminant Analysis[J].Journal of the American Statistical Association，2015,110(510).

[12] 张景肖，李向杰，郭海明.HDSIS超高维数据稳健变量筛选[J].统计与信息论坛，2016，31(4).

[13] Liu J，Zhong W，Li R.A Selective Overview of Feature Screening for Ultrahigh-Dimensional Data[J].Science China Mathematics，2015,58(10).

[14] Barut E， Fan J， Verhasselt A.Conditional Sure Independence Screening[J].Journal of the American Statistical Association， 2016,111(515).

[15] Wang L，Liu J，Li Y，Li R.Model-free Conditional Independence Feature Screening for Ultrahigh Dimensional Data[J].Science China Mathematics，2017,60(3).

[16] Zhong W，Zhu L.An Iterative Approach to Distance Correlation Based Sure Independence Screening[J].Journal of Statistical Computation and Simulation，2015,85(11).

[17] Segal M，Dahlquis K，Conklin B.Regression Approach for Microarrary Data Analysis[J].Journal of Computational Biology,2003,10(6).