采用桥臂电抗投切控制的MMC降电容运行方法
2018-04-16屈海涛赵成勇许建中曹均正
李 帅, 屈海涛, 赵成勇, 许建中, 曹均正
(1. 新能源电力系统国家重点实验室(华北电力大学), 北京市 102206; 2. 中电普瑞电力工程有限公司, 北京市 102200)
0 引言
模块化多电平换流器(modular multilevel converter,MMC)在2003年被首次提出[1],与基于晶闸管的传统直流换流器和基于两电平电压源换流器的柔性直流换流器相比,具有以下优势[2-4]:①结构的模块化使得系统易于扩展,从而能够实现更高的电压等级,方便构建的冗余结构也提高了系统的可靠性;②开关频率低,降低了开关损耗;③可以产生更多的电平数,波形质量高,无需安装交流滤波器;④无需采用功率开关器件直接串联成阀来提高电压等级,对器件的要求降低,制造难度下降。
然而,MMC也存在子模块电容电压波动难以抑制的问题,使交流侧输出电压出现偏差,影响波形质量[5],限制了子模块电容值的进一步减小,而子模块电容值与换流器体积、造价紧密相关。
针对MMC电容电压波动的抑制,国内外学者进行了深入的研究并提出了有效的解决思路。文献[6]对子模块电容电压波动的产生机理进行了详细的数学分析,但并未提出波动抑制方案。文献[7]针对桥臂上存在的二倍频环流分量,设计了二倍频环流抑制控制器,但这种方法无法应用于三相不平衡工况。文献[8]提出了一种基于MMC环流模型的通用环流抑制控制(circulating current suppressing control,CCSC)策略,从而降低了子模块电容电压波动,其实现原理简单,无需负序坐标变换和相间解耦环节,但控制精度低于负序坐标变换策略。文献[9]设计了一种附加控制器来抑制子模块电容电压波动,但由于需要进行复杂的两倍频负序旋转坐标变换,设计较为复杂。文献[10]提出了一种用于确定最优注入环流的优化算法,但随着工况的变化,对计算的实时性要求较高。文献[11]引入准比例谐振控制器用于控制MMC内部环流,简化了控制过程但无法进一步改善电容电压波动的抑制效果。
以上方法仅从环流抑制角度达到降容的目的,文献[12]提出了一种调制波注入三次谐波的方法,可起到降低换流器损耗及子模块电容电压波动的作用,但由于半桥MMC最大调制比仅为1.15,限制了降容的效果。文献[13]对半桥加全桥混合子模块及其均压策略进行了详细的研究,由于全桥子模块的加入,可使换流器电压调制比进一步升高,但该方案需要大量增加绝缘栅双极型晶体管(IGBT)的使用数量,成本和运行损耗较高。
文献[14]提出了一种含中间子模块的MMC改进拓扑,其中间子模块不含基频电压波动,顶部子模块和底部子模块不含基频与二倍频电容电压波动,降容效果较好,但该方案下不同位置的MMC子模块接线方式不同,较难改造。
本文在参考文献中提出的环流与子模块电容电压波动关系的基础上,提出了一种桥臂电抗投切控制(arm reactor switching control,ARSC)策略,以降低子模块电容电压波动;对其作用机理进行了分析并设计了相应的控制策略;在PSCAD/EMTDC仿真环境下验证了拓扑的有效性,并与CCSC的作用效果进行了对比;从经济性角度将ARSC与CCSC进行了对比。
1 ARSC结构及其运行方式
本文提出的ARSC需要在MMC半桥换流器拓扑的桥臂电抗处做出改动,将桥臂电抗接成电抗器子模块的形式。主电路结构如图1所示,图中uva,uvb,uvc分别为a,b,c三相交流侧电压。MMC三相换流器各相单元均由上、下两桥臂,桥臂电感和电抗子模块组成。上、下两桥臂中各包含N个MMC子模块,该子模块采用半桥型结构,由两个IGBT(均配置有续流二极管)和一个子模块电容组成。
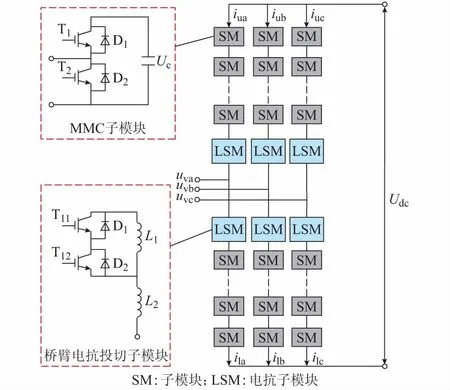
图1 含桥臂电抗投切子模块的MMC拓扑Fig.1 Topology of MMC with arm reactor switching sub-module
在传统MMC半桥换流器的基础上,将桥臂电抗的固定接入改为灵活投入的方式,将桥臂电感分为灵活投切部分L1和固定投入部分L2。桥臂的总电抗值为:
L=L1+L2
(1)
由图1可知,桥臂电抗投切子模块的电感L1上并联有反向串联的IGBT,IGBT的数量由L1的实际承压水平决定,每个IGBT都配置有续流二极管。这里为了简化分析,只写出两个IGBT模块。该子模块的运行方式如图2(a)所示。
1)电抗器切除:当开关管T11和T12同时被触发时,该子模块的电抗器被短接,电流由开关管流过。
2)电抗器投入:当开关管T11和T12同时关断时,电流流过电抗器,等同于将该电抗器直接串联入桥臂电路。
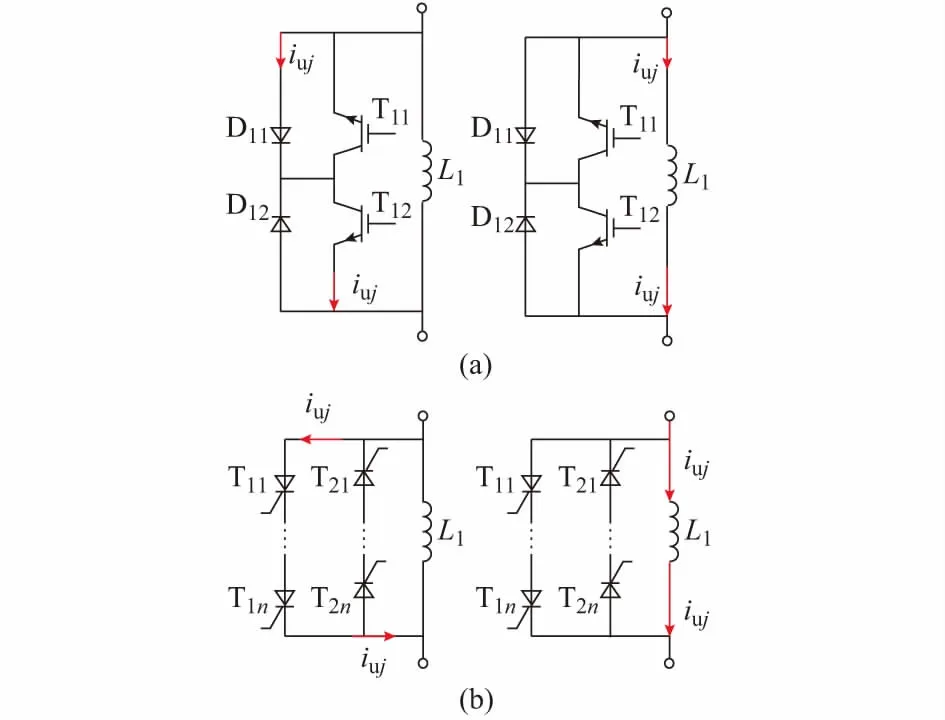
图2 电抗子模块运行方式Fig.2 Operation mode of reactor sub-module
由于IGBT成本较高,且电抗器的每次投入或切除状态下的电流方向不变,而关断时开关管会承受反压,所以可利用晶闸管的半控特性与单向导通特性来实现电抗器的投切。本文设计的基于晶闸管的替代方案如图2(b)所示,晶闸管T11-T1n与T21-T2n反向并联,其中T11-T1n只在逆变工况下触发或关断,整流状态下保持闭锁状态,T21-T2n反之。本文如无特别说明,将采用基于晶闸管的电抗子模块进行分析和仿真。
2 ARSC控制原理与对比分析
2.1 ARSC控制原理
文献[6]指出,增大桥臂电感可以有效降低环流的幅值,进而抑制子模块电容电压波动。但提高桥臂电感仅能起到降低环流的作用,与CCSC效果相当但经济性较差。
在传统MMC半桥换流器拓扑中,假定MMC的3个相单元的参数完全相同,相单元对于直流电压Udc来说具有相同的阻抗,因此可以认为直流电流在3个相单元中平分;同样,由于MMC上、下桥臂参数对称,可以认为交流电流在上、下桥臂平分。忽略内部环流,则上下桥臂电流可以表示为[15]:
(2)
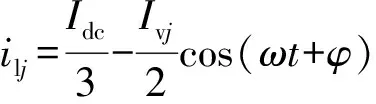
(3)
式中:Idc为直流母线电流;iuj和ilj分别为MMC各相上下桥臂电流;Ivj为MMC各相交流侧电流幅值;j=a,b,c;ω为基波角频率;φ为初相角。
由于电抗对交流电流的影响较大,当上下桥臂电抗值不同,即上下桥臂参数不对称时,可以在较大程度上影响上下桥臂的电流分布,其中电抗值较大的桥臂电流分量较小,电抗值较小的桥臂电流分量较大。
为了简化分析桥臂电抗的改变对输出交流电流分量的影响,这里只对MMC的a相等效电路进行分析,如图3所示,同样的分析也适用于b,c两相。其中输出阻抗的电阻部分用R表示,电感部分统一归到桥臂电抗部分用L1和L2表示,uG为MMC直流侧等效钳位点电压。
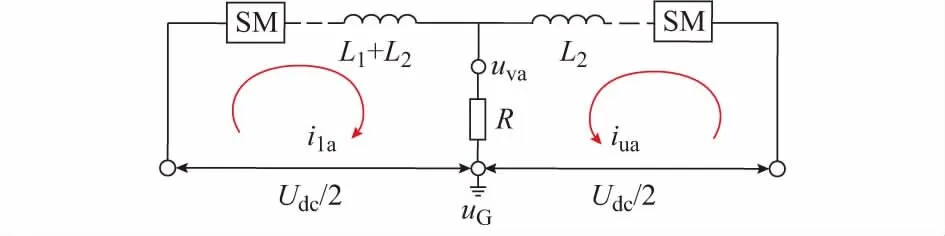
图3 a相MMC等效电路Fig.3 Equivalent circuit of a-phase MMC
根据叠加原理,该相上下桥臂输出总电流的交流分量为:
i=iua+ila
(4)
通过ARSC,将上桥臂的可投切电抗器(电感值为L1)切除,下桥臂部分的可投切电抗器(电感值为L1)投入,由基尔霍夫定律可得:
(5)
(6)
式中:uva为交流系统a相网侧电压,满足uva=Uvacos(ωt+θ),其中Uva为a相网侧电压幅值;uua和ula分别为a相上下桥臂电压,根据MMC的运行特性可得
(7)
(8)
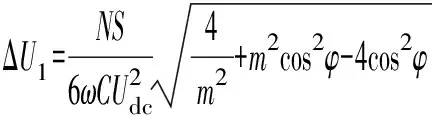
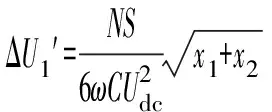
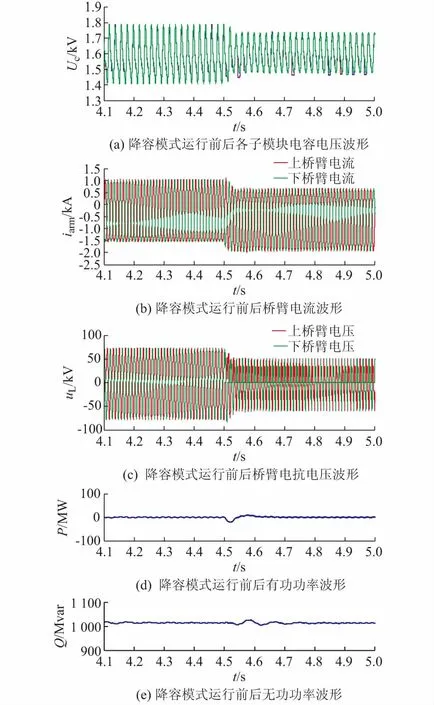
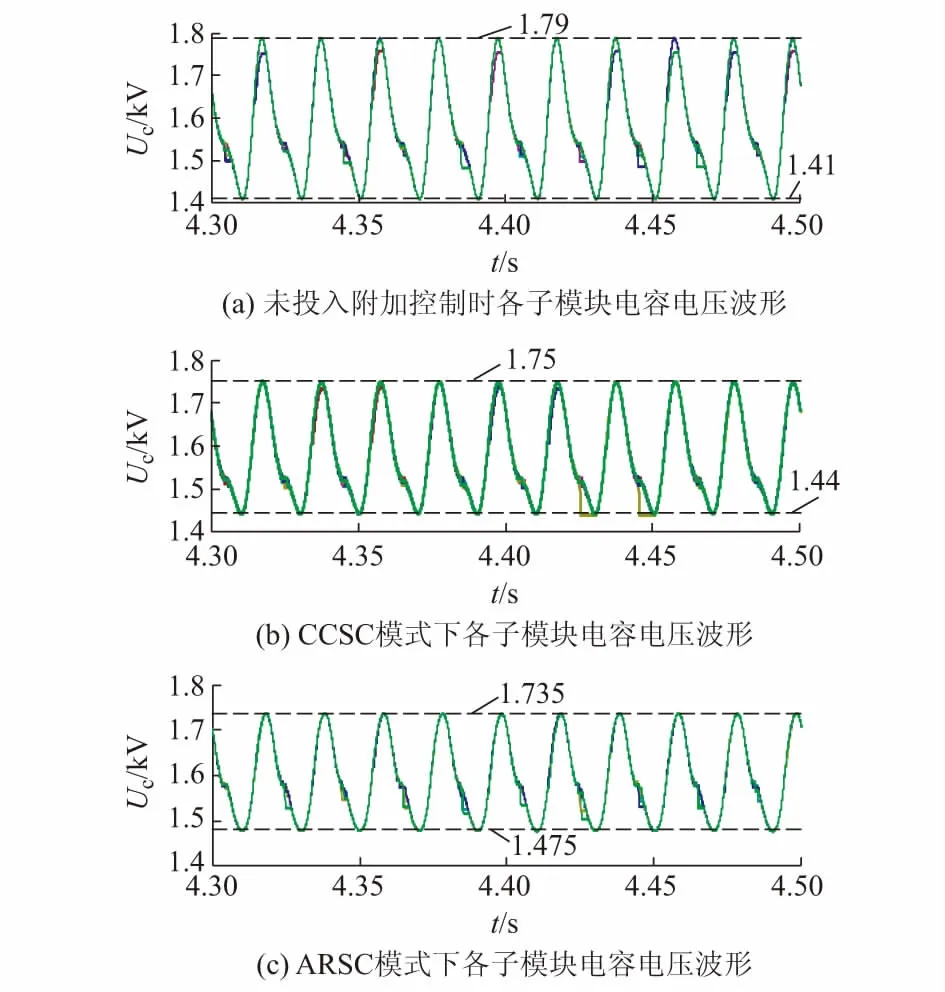
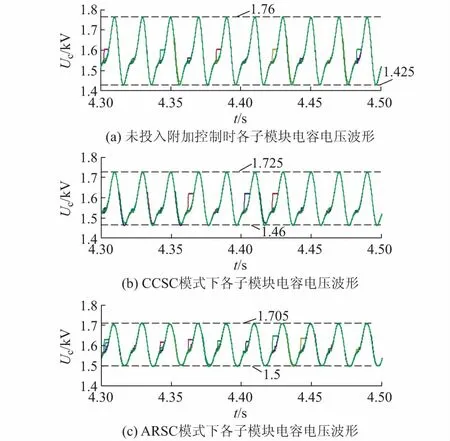
式中:m为调制比,定义为m=2U/Udc,通常情况下有0 代入式(5)、式(6)可求得上下桥臂电流分别为: (9) (10) 其中 (11) 则可知上下桥臂基频交流电流有效值的变化量ΔI可以表示为 (12) 可见,随着上桥臂电抗值的减小,桥臂电流的有效值将随之增大,由于IGBT和二极管通流能力的限制,为了保证器件的安全裕度,应确保桥臂电抗被切除的半个工频周期的桥臂电流不超过器件额定值(另外半个工频周期由于可投切桥臂电抗的投入,桥臂电流将大幅降低,故可以不予考虑)。因此,可通过式(12)和IGBT模块的参数来作为电抗L1和L2选取的约束条件,以保证电流有效值不超过所用器件的允许范围,在达到最优降容效果的同时满足可靠性的要求。 在上下桥臂电抗的不对称投入运行工况下,每相上下桥臂电流可以表示为: (13) (14) 换流器的上下桥臂各有N个子模块,且每个桥臂投入的子模块个数从0到N变化。由MMC的运行原理可知:①只有处于投切状态的子模块才会因充放电而产生电压波动;②处于工作状态的MMC子模块之间为串联关系,故同一时刻充放电速率相同;③MMC上下桥臂对称运行,上下桥臂子模块投入个数之和为固定值。 因此,在排序频率足够高的情况下,同一时刻下桥臂等效电容值与处于投入状态中的子模块个数之间的关系可以表示为: (15) (16) 式中:Ceq为该桥臂对外等效电容;n为处于投入状态的子模块数量;Ci为第i个子模块的电容值。 由式(15)、式(16)可见,处于投入状态的子模块数量较少的桥臂等效电容值较大,在同样的排序频率下,子模块电容电压波动幅值小于子模块数量较多的另一桥臂。因此,可通过增加该桥臂电流和抑制另一桥臂电流的方式降低整体电容电压波动幅值,进而抑制整体波动水平。 为了从数学原理上说明ARSC与CCSC的区别,首先列写了MMC子模块电容电压表达式[16],分别得出CCSC与ARSC对子模块电容电压的基频与二倍频分量的影响,以对比二者的投入对子模块电容电压的基频与二倍频分量的作用。 在非理想状态下,桥臂电流除了直流分量和基频交流分量,还包含以二次环流为主的内部环流。以A相为例,忽略幅值较低的高次环流,此时上下桥臂的电流可以表示为: (17) (18) 式中:I2f为二倍频环流的幅值;φ2f为二倍频的初相角。 可以看出,二倍频环流按负序在三相间流动,因此可以采用两倍频负序的旋转坐标变换把二倍频环流分解为两个直流分量。 CCSC的原理为将式(17)、式(18)相加除以2,得到不平衡电流icia,使其经过两倍频负序的旋转坐标变换分解为直流量,与参考值(通常取0)作差再经比例—积分(PI)控制器得到电压参考值,引入电压调制,从而消除二倍频环流分量。消除环流分量后的桥臂电流即可由式(2)、式(3)表示。 表征上下桥臂各子模块开关状态的开关函数可以表示为: (19) (20) 假设排序频率足够大,则各子模块电容电压保持一致,有 (21) (22) 式中:ucua和ucla分别为上下桥臂上任一子模块的电容电压;C为子模块电容值。 式(21)和式(22)中,由交直流侧有功功率平衡约束得到: (23) 则由式(21)至式(23)可得上下桥臂子模块的电压为: ucua=Ucref+UcrefΔU1sin(ωt+φ)+ UcrefΔU2sin(2ωt+φ2f) (24) ucla=Ucref-UcrefΔU1sin(ωt+φ)+ UcrefΔU2sin(2ωt+φ2f) (25) 其中 (26) (27) 式中:S为视在容量;Ucref为子模块电容电压额定值,即Udc/N;ΔU1和ΔU2分别为电压基频、二倍频的波动幅值。 无CCSC作用时,考虑到高次谐波幅值较小,对电容电压波动的影响较小,为了简化分析,只列写基频和二倍频的表达式,得到此时上下桥臂子模块电压表达式为: ucua′=Ucref(1+ΔU1′sin(ωt+φ)+ ΔU2′sin(2ωt+φ2f)) (28) ucla′=Ucref(1-ΔU1′sin(ωt+φ)+ ΔU2′sin(2ωt+φ2f)) (29) 其中 (30) (31) 且有 (32) (33) (34) 对比式(24)至式(27)与式(28)至式(34)可知,x2和x3部分被CCSC环节消除。因此采用CCSC消除了桥臂上的二倍频环流后,子模块电压的基频与二倍频分量得到了一定程度的减少。 将式(30)和式(31)展开,可得以电流为变量的基频二倍频幅值表达式为: (35) (36) 式中:Ix为桥臂电流交流分量的幅值。 结合式(12)可知,通过ARSC可改变桥臂电流的交流分量Ix,进而可以成比例地改变子模块电容电压的基频与二倍频分量,而CCSC仅减少了x2与x3部分,无法具有更宽的调节范围。 对于子模块投入数较多的桥臂,通过ARSC控制可使子模块的基频和二倍频电压波动减小,而另一桥臂由于等效电容的增加,子模块受基频、二倍频影响的波动幅值均降低,所以适当调节电抗子模块的电感值来分配上下桥臂的交流分量,可以使整体子模块电压波动减小。 在本文所提出的控制策略下,根据上下桥臂投入子模块个数的大小关系,分配上下桥臂的电抗值,使得每一时刻上下桥臂之间电抗值不变,但上桥臂或下桥臂与交流侧始终有一个电抗器处于投入状态,从而改变桥臂原有能量分布,以减小整体的子模块电压波动。 考虑到当上下桥臂投入子模块个数之和为N,当投入子模块个数为N/2时,上下桥臂投入子模块个数相同。为了不影响上下桥臂的对称性,将上下桥臂投入临界点选择为N/2子模块个数,当MMC作为逆变站运行时设计如下控制。 1)当上桥臂投入子模块数低于N/2并将继续减少,即nup 2)当上桥臂投入子模块数nup>N/2时,上桥臂电抗投切晶闸管将承受反压而关断,从而将电抗投入到电路中,此时通过控制单元触发下桥臂电抗投切开关管T11-T1n,使下桥臂电抗处于切除状态。此时上桥臂电抗将因T11-T1n承受反压迅速截止而投入,电抗值大于下桥臂电抗值而使上桥臂流过电流减小,所以等效子模块电容值较低的上桥臂电容电压波动减小。 当MMC处于整流站运行时,由于晶闸管的单向导通特性,此时控制触发的是开通方向与T11-T1n相反的T21-T2n开关管,而T11-T1n开关管始终处于闭锁状态,其他控制策略与逆变站相同。 在PSCAD/EMTDC环境下搭建了双端401电平MMC柔性直流输电系统仿真模型。其中一端定直流电压控制:直流电压给定值为640 kV,无功功率为0 Mvar;另一端定有功功率为1 000 MW,无功功率为0 Mvar。系统详细参数如附录A表A1所示。 为了体现ARSC方案的优势,将其与非降容运行状态下的传统MMC方案及CCSC方案进行对比分析,以验证子模块电容纹波的抑制效果。三种方案的每个桥臂电抗均为0.150 1 H。对于ARSC方案,每个桥臂的固定电抗值为0.000 1 H,可投切的桥臂电抗值为0.15 H。在4.5 s前,所有桥臂的电抗器子模块中的开关管均处于闭锁状态,即电抗器处于工作状态,与传统MMC拓扑及CCSC模式的运行状态相同。 图4显示ARSC方案运行前后的对比波形,4.5 s时按照所设计的控制策略对电抗器子模块进行投切控制。控制启动之后所有子模块的电容电压波动幅度均迅速降低,其中a相上桥臂子模块电容电压波形如图4(a)所示。a相上下桥臂电流如图4(b)所示,其中正向桥臂电流值降低,反向电流值相应增大,所以每周期桥臂子模块部分流过的电流有效值不变,且流过IGBT的电流有效值降低,流过续流二极管的电流有效值相应升高。 图4(c)显示了降容模式前后a相上下桥臂电抗电压波形,由图可见降容运行之后桥臂电抗电压有效值得以较大幅度降低,从而降低了对桥臂电抗投切晶闸管的耐压要求;图4(d)和(e)显示控制过程中系统有功功率、无功功率经过短暂的波动之后恢复为正常值。 为了直观显示晶闸管开通和关断时刻,附录B图B1展示了a相上下桥臂电抗器投切晶闸管开通和关断的时序图。为了使开关状态与调制波对应,将常见的双窄脉冲触发改为方波触发,在输出高电平时触发晶闸管导通,低电平时停止触发。 图4 降容模式运行前后波形对比Fig.4 Comparison of waveforms before and after capacitance reduction operation 为了同时显示方波与调制波之间的关系,将高电平的刻度设为100,而正弦调制波的取值范围为0~400,对应该桥臂的400个子模块。可知,当桥臂开通子模块个数小于200时,触发导通该桥臂电抗投切晶闸管,从而将桥臂电抗旁路,当开通个数大于200时,停止触发该晶闸管,随后晶闸管将因电流过零而截止,从而将桥臂电抗投入到桥臂中,同一时刻上下桥臂只有一个桥臂电抗处于投入状态。 4.3.1整流站仿真结果 图5(a)(b)(c)分别显示无降容控制措施、CCSC方案、ARSC方案下,MMC子模块在同等系统参数与工况下的电容电压波动曲线。由图可知,CCSC的投入可以将电容电压波动的波峰波谷差值降低18.4%,如图5(b)所示。而未采用其他辅助降容控制的ARSC拓扑方案的投入可将电容电压波动的峰谷差降低31.5%,如图5(c)所示。 图5 整流模式下ARSC与CCSC的降容效果对比Fig.5 Comparison of capacitance reduction effect by ARSC and CCSC under rectification mode 4.3.2逆变站的仿真结果 图6(a)(b)(c)分别显示无降容控制措施、CCSC方案、ARSC方案下的MMC系统在逆变工况下的电容电压波动曲线。此时有功功率仍为系统的最大功率1 000 MW,由图可知CCSC的投入可以将电容电压波动的波峰波谷差值降低21%,如图6(b)所示。而采用ARSC方案可将电容电压波动的峰谷差降低39%,如图6(c)所示。 图6 逆变模式下ARSC与CCSC的降容效果对比Fig.6 Comparison of capacitance reduction effect by ARSC and CCSC under inverter mode 4.3.3子模块电容电压FFT分析 通过对整流工况下的MMC子模块电容电压进行快速傅里叶变换(FFT)分析,得到了非降容运行工况、CCSC方案、ARSC方案下的子模块电容电压波动的基频分量幅值分别为:0.131 4,0.113 2,0.097 4 kV;二倍频分量分别为:0.064 4,0.043 5,0.028 1 kV;三倍频分量分别为:0.006 3,0.001 7,0.002 0 kV。幅值对比如附录C图C1所示。 经过对比可知,ARSC方案下的基频、二倍频、三倍频电容电压波动分量相比于另外两种方案都有所降低,与本文第2节的分析结果相符。 考虑到半桥串全桥混合子模块方案和三次谐波注入方案主要是从提高电压调制比的角度出发从而达到降容效果,而CCSC方案和ARSC方案主要是对桥臂电流的基频和二倍频分量进行附加控制来达到降容效果,后两种方案可以在前两种方案的基础上进一步增强该效果。所以本节主要对机理类似的CCSC方案和ARSC方案开展经济性对比分析。 本节所选用的器件型号如下:晶闸管型号为T2871N80TOH,其参数为8 kV/2.6 kA,厂商为英飞凌[17];IGBT型号为5SNA 1500E330305,参数为3.3 kV/1.5 kA,厂商为ABB[18]。 CCSC方案采用纯控制的方法达到抑制环流以降低子模块电容电压波动的作用,因此仅需要额外消耗计算资源,增加的硬件投资成本可以忽略不计,即可实现电容电压波动降低18.4%以上,即同样电容纹波要求下,电容值可以降低18.4%,电容的成本、重量、体积均可有效降低。 对于ARSC方案,所选晶闸管可承受90 kA持续时间为10 ms的冲击电流。为了提高可靠性,考虑电压安全裕度,在本文中其安全承压设计值为4 kV。 由于所提方案下桥臂电抗承压极值为50 kV,考虑安全余量可设计承压为80 kV的投切开关,所以每个桥臂所需晶闸管数量为20×2个,三相六桥臂共需240个晶闸管及相应的晶闸管串联均压电路。为防止故障情况的过电压,每组晶闸管均需额外配置保护电压为80 kV的避雷器。另外,由于桥臂电抗在晶闸管导通的过程中被旁路掉,投入时间得以减少,电流的热效应也得以缓解,可以选择额定电流较低的电抗器以降低成本。根据仿真结果可知,采用该方案的电容纹波幅值降低约31.5%,等同于纹波幅值不变的情况下电容容值降低31.5%。 综上所述,ARSC方案相比于CCSC方案能够进一步降低约16%的电容值。考虑到电容重量和体积在子模块中占比较大,有效降低电容值能够从一定程度上实现柔直换流阀的轻型化。由于换流器子模块数量众多,仿真模型为2 400个子模块(不含冗余),有效降低电容值能够大幅降低系统整体造价,具有一定的工程意义。 5.2.1损耗组成 对于桥臂子模块部分,根据文献[19-21],损耗的主要来源是IGBT、二极管的开关损耗与通态损耗。IGBT和二极管导通损耗的计算公式分别如下: PTcon=UCEIC=(RTIC+UCE0)IC (37) PDcon=UDID=(RDID+UD0)ID (38) 式中:UCE为IGBT集电极和发射极之间的电压;UD为二极管两端电压;IC和ID分别为IGBT与二极管的工作电流;RT和RD分别为IGBT与二极管的导通电阻,与结温有关;UCE0和UD0分别为IGBT和二极管的通态压降,与结温有关。 IGBT和二极管的开关损耗计算公式如下[22]: (39) (40) (41) 式中:a1,b1,c1,a2,b2,c2,a3,b3,c3为拟合系数;Eon为IGBT单次开通消耗的能量;Eoff为IGBT单次关断消耗的能量;EDrec为二极管单次反向恢复消耗的能量。由上式可知开关损耗与开关频率密切相关。 桥臂电抗投切部分的损耗来源于晶闸管,分为通态损耗和开关损耗[23]。 晶闸管的通态损耗计算公式为: (42) 式中:nT为串联的晶闸管个数;UT0为晶闸管门槛电压;rT为晶闸管通态电阻平均值;R为晶闸管间通态电阻平均值;ITAV为晶闸管平均电流值;ITRMS为晶闸管电流有效值。 晶闸管开关损耗的计算公式为: PTon=3×2nTfPwon (43) PToff=3×2nTfPwoff (44) 式中:PTon为晶闸管开通损耗;PToff为晶闸管关断损耗;Pwon为晶闸管单次开通损耗;Pwoff为晶闸管单次关断损耗;f为工作频率。 5.2.2CCSC与ARSC损耗对比 对于IGBT,由附录D表D1、表D2中的IGBT模块在结温125 ℃时的参数,可通过式(37)至式(41)计算得出通态损耗与开关损耗;对于晶闸管,由器件手册可知UT0为1.267 V,R为0.366 mΩ,Pwon为0.001 9 kW,Pwoff为0.011 5 kW。因此可通过式(42)至式(44)计算出开关损耗与通态损耗。 根据式(37)至式(44),通过仿真模型计算得出三种方案下的单端MMC的损耗功率,其中ARSC方案的换流器通态损耗为6.81 MW,开关损耗为7.14 MW,其中通态损耗包含投切晶闸管的通态损耗0.19 MW,开关损耗包含投切晶闸管的开关损耗0.08 MW,该方案下晶闸管投切新增的损耗占换流器总损耗的1.9%;CCSC方案下的开关损耗和通态损耗分别为7.05 MW和6.66 MW;非降容运行工况下的开关损耗和通态损耗分别为7.05 MW和6.96 MW。由以上数据可知,ARSC方案下的换流器损耗比非降容工况下的总损耗低约0.4%,比CCSC工况高约1.8%。 相比于CCSC,ARSC能够在同样开关频率下进一步降低至少16%的电容纹波幅值,因此能够允许牺牲部分电容纹波幅值的抑制效果以降低开关频率,进而能够显著降低系统的开关损耗水平,有利于在投资成本与运行成本之间进行折中。 本文针对柔直换流阀轻型化面临的问题之一,即子模块电容体积和重量较难降低的问题,从MMC拓扑结构的角度,主要进行了如下工作:①提出了一种降容运行策略ARSC,并描述了其运行方式;②对比分析了CCSC和ARSC的降容原理;③在PSCAD/EMTDC环境下,搭建了采用ARSC策略的两端柔性直流输电系统仿真模型,并进行了仿真分析;④对CCSC与ARSC的经济性进行了分析。得出了以下结论。 1)相比于CCSC,ARSC可在更大程度上调节子模块电容电压波动中占主导的基频、二倍频分量。 2)PSCAD仿真的工况中,在保证系统正常运行的前提下,所提策略能够达到比CCSC更好的降容效果。 3)所提MMC拓扑需要增加晶闸管等器件以对桥臂电抗器进行投切控制,考虑到子模块数量众多且电容器造价较高,而晶闸管成本相对较低且新增数量有限,所以子模块电容体积和容值的降低能够换来更好的经济性,有利于实现MMC换流阀的轻型化。 4)对于ARSC方案下的MMC开关频率、运行损耗,以及子模块电容电压纹波幅值的综合优化,本文所做的工作还不充分,有待进一步深入研究。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 [1] LESNICAR A, MARQUARDT R. An innovative modular multilevel converter topology suitable for a wide power range[C]// IEEE Power Technology Conference, June 23-26, 2003, Bologna, Italy: 6p. [2] 徐政.柔性直流输电系统[M].北京:机械工业出版社,2013. [3] DEBNATH S, QIN Jiangchao, BAHRANI B, et al. Operation, control, and applications of the modular multilevel converter: a review[J]. IEEE Transactions on Power Electronics, 2014, 30(1): 35-37. [4] 杨晓峰,林智钦,郑琼林,等.模块组合多电平变换器的研究综述[J].中国电机工程学报,2013,33(6):1-14. YANG Xiaofeng, LIN Zhiqin, ZHENG Qionglin, et al. A review of modular multilevel converters[J]. Proceedings of the CSEE, 2013, 33(6): 1-14. [5] 雷鸣,李耀华,葛琼璇,等.MMC变流器模块电压波动对输出电压的影响[J].电机与控制学报,2014,18(3):25-33. LEI Ming, LI Yaohua, GE Qiongxuan, et al. Effects of the module voltage fluctuation on the output voltage of modular multilevel converter[J]. Electric Machines and Control, 2014, 18(3): 25-33. [6] 周月宾,江道灼,郭捷,等.模块化多电平换流器子模块电容电压波动与内部环流分析[J].中国电机工程学报,2012,32(24):8-14. ZHOU Yuebin, JIANG Daozhuo, GUO Jie, et al. Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters[J]. Proceedings of the CSEE, 2012, 32(24): 8-14. [7] TU Q, XU Z, XU L. Reduced switching-frequency modulation and circulating current suppression for modular multilevel PWM converters[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 2009-2017. [8] 杨晓峰,郑琼林.基于MMC环流模型的通用环流抑制策略[J].中国电机工程学报,2012,32(18):59-65. YANG Xiaofeng, ZHENG Qionglin. A novel universal circulating current suppressing strategy based on the MMC circulating current model[J]. Proceedings of the CSEE, 2012, 32(18): 59-65. [9] 高航,苏建徽,汪晶晶,等.模块化多电平型换流器电容电压二倍频波动抑制策略研究[J].电力系统保护与控制,2014,42(6):116-122. GAO Hang, SU Jianhui, WANG Jingjing, et al. Study on control strategy for suppressing double fundamental frequency fluctuation of capacitor voltage of modular multilevel converter[J]. Power System Protection and Control, 2014, 42(6): 116-122. [10] PICAS R, POU J, CEBALLOS S, et al. Optimal injection of harmonics in circulating currents of modular multilevel converters for capacitor voltage ripple minimization[C]// IEEE ECCE Asia Downunder, June 3-6, 2013, Melbourne, Australia: 318-324. [11] 黄守道,彭也伦,廖武.模块化多电平型变流器电容电压波动及其抑制策略研究[J].电工技术学报,2015,30(7):63-71. HUANG Shoudao, PENG Yelun, LIAO Wu. Study of capacitor voltage fluctuation and its suppression for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 63-71. [12] LI R, FLETCHER J E, WILLIAMS B W. Influence of third harmonic injection on modular multilevel converter-based high-voltage direct current transmission systems[J]. IET Generation, Transmission & Distribution, 2016, 10(11): 2764-2770. [13] LU Maozeng, HU Jiabing, ZENG Rong, et al. Imbalance mechanism and balanced control of capacitor voltage for a hybrid modular multilevel converter[J/OL]. IEEE Transactions on Power Electronics[2017-08-24]. DOI: 10.1109/TPEL.2017.2743780. [14] LI Binbin, ZHANG Yi, WANG Gaolin, et al. Modified modular multilevel converter with reduced capacitor voltage fluctuation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6018-6119. [15] 李凯,赵争鸣,袁立强,等.基于能量平衡的降低模块化多电平变换器子模块电容电压波动控制策略[J].电工技术学报,2017,32(14):17-26. LI Kai, ZHAO Zhengming, YUAN Liqiang, et al. Reduced modular multi-level transformer sub-module capacitance voltage fluctuation control strategy based on energy balance[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 17-26. [16] LI Z, WANG P, CHU Z, et al. An inner current suppressing method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4873-4879. [17] Infineon Technologies. Datasheet thyristor T2871N[EB/OL]. [2014-11-02]. http://www.infineon.com. [18] ABB Switzerland Ltd. Datasheet IGBT 5SNA 1500E330305[EB/OL]. [2014-07-19]. http://new.abb.com/products/semiconductors. [19] Determination of power losses in voltage sourced converter (VSC) valves for HVDC system: Part 1general requirements: IEC 62751[S]. 2012. [20] Determination of power losses in voltage sourced converter (VSC) valves for HVDC system: Part 2modular multilevel converter: IEC 62751[S]. 2012. [21] Determination of power losses in high-voltage direct current (HVDC) converter stations with line commutated converters: IEC 61803[S]. 2016. [22] 张哲任,徐政,薛英林.基于分段解析公式的MMC-HVDC阀损耗计算方法[J].电力系统自动化,2013,37(15):109-116. ZHANG Zheren, XU Zheng, XUE Yinglin. Valve loss calculation of MMC-HVDC based on piecewise analytical formula[J]. Automation of Electric Power Systems, 2013, 37(15): 109-116. [23] 李海生.TCR支路损耗研究[D].南宁:广西大学,2013. 李帅(1986—),男,通信作者,博士研究生,主要研究方向:柔性直流输电。E-mail: lishuaiwork@foxmail.com 屈海涛(1983—),男,工程师,主要研究方向:柔性直流输电。E-mail: haitaoqu@163.com 赵成勇(1964—),男,教授,博士生导师,主要研究方向:高压直流输电、混合直流输电。E-mail: chengyongzhao2@126.com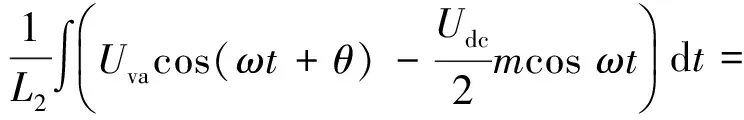
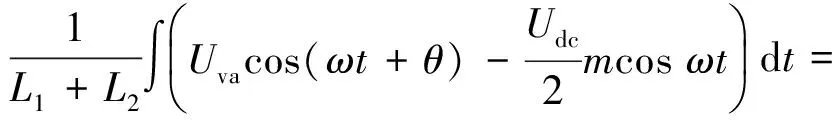
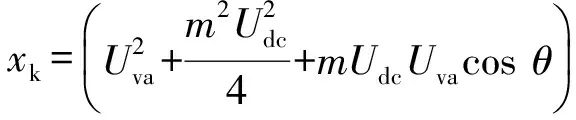
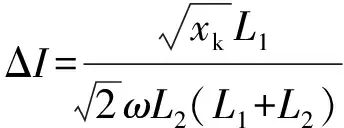
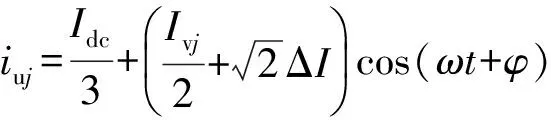
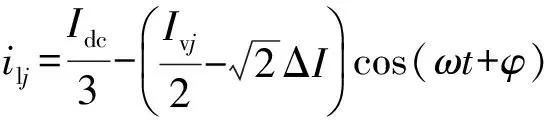
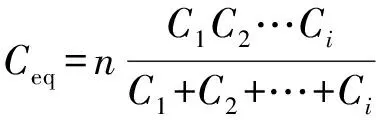
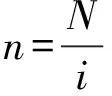
2.2 ARSC与CCSC抑制电容电压波动机理对比
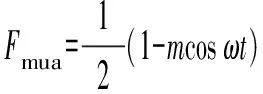
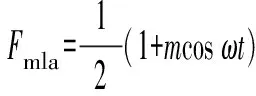
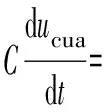
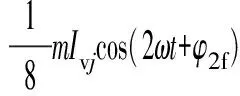
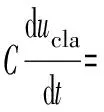
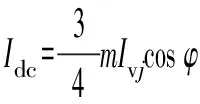
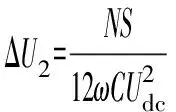
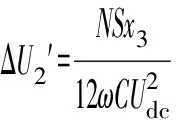
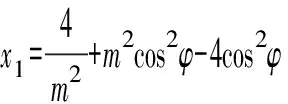
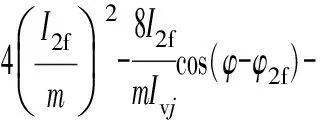
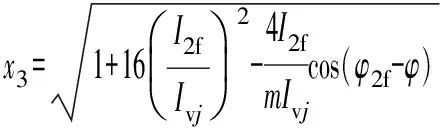
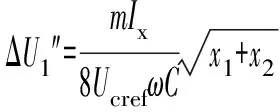
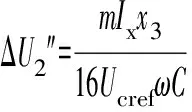
3 ARSC控制时序
4 仿真验证
4.1 仿真模型
4.2 ARSC方案仿真结果
4.3 ARSC方案与CCSC方案仿真对比
5 经济性分析
5.1 造价分析
5.2 损耗分析
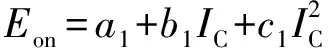
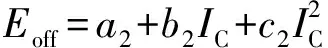
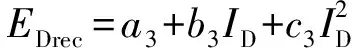
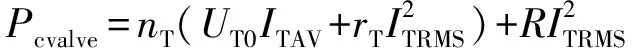
6 结语
