电网电压对称骤升时DFIG暂态电流分析及限流电阻阻值优化

孙丽玲, 王艳娟

(华北电力大学电气与电子工程学院, 河北省保定市 071003)

0　引言

双馈感应风力发电机(DFIG)以其换流器容量较小、有功和无功功率解耦控制、调速范围宽等优点一直占据着风电市场的主要份额[1-2]。但是,DFIG定子绕组与电网直接相连,使其对电网电压故障尤为敏感,故障穿越能力也极具挑战性。目前,低电压穿越技术相对成熟且已取得了一定的研究成果,但高电压穿越 (high voltage ride-through,HVRT)技术尚未引起足够的关注[3-7]。HVRT同样也是风电大规模并网运行的关键技术之一。电网电压骤升故障同样对DFIG定转子造成强烈的冲击,为确保DFIG在电网电压骤升时仍能并网运行,有必要对HVRT下的转子电流特性进行分析。

电网电压故障时转子电流的精确分析关系到故障穿越的实现和故障特性的分析。已有较多文献对电网电压严重故障导致转子保护投入时的短路电流特性进行了研究[8-12],但均未涉及换流器的调控分析和HVRT时转子电流特性研究。文献[13-14]给出了计及换流器调控作用时,转子电流在时域中的解析表达式;文献[15]在分析换流器调节特性对故障电流影响的基础上给出了故障电流解析表达式，不同于三相短路情况,HVRT期间的转子电流特性由于撬棒保护并未投入[16]。此外,常规研究大多集中于故障期间转子电流特性分析,在计算转子电流最大值时只考虑了故障发生时刻,忽略故障切除后DFIG的动态变化,存在故障电压升高的暂态过程尚未结束,转子电流的暂态分量尚未衰减完毕,导致故障切除时暂态过程叠加使转子电流大于故障发生时刻,使得HVRT期间转子电流最大值计算不准确,进而导致限流电阻阻值整定偏小。本文综合分析了故障发生和切除时转子电流的变化,推导电网故障发生而致电压骤升、故障切除及其后的转子电流表达式。

忽略故障切除后转子电流的动态变化,导致DFIG在HVRT期间转子电流暂态特性分析不全面,进而影响HVRT控制策略的制定,如基于转子串联电阻电路中限流电阻阻值整定。文献[17]仅提出可以利用转子串电阻方法解决撬棒电路的失控问题,但对转子串电阻保护的相关信息并未进行说明;文献[18]分析了基于转子串电阻的DFIG故障穿越技术,但在限流电阻阻值整定时,认为转子故障电流的最大值出现在故障期间;文献[19]采用转子串电阻和静止同步补偿器(STATCOM)的综合保护方案以协调多风电场间的故障穿越问题。若按上述整定方式会使HVRT时所选取的限流电阻偏小,不能抑制故障切除后的转子过电流。

针对以上不足,本文在对电磁暂态全过程分析的基础上,推导出电网电压对称骤升故障下的转子电流表达式。忽略故障切除后转子电流的变化,将导致采用转子串电阻电路实现HVRT时限流电阻阻值的整定偏小,无法完成电网电压恢复后的HVRT。在此基础上对限流电阻阻值进行优化,对DFIG的HVRT研究具有一定的指导意义。

1　对称骤升故障下的DFIG暂态特性分析

为分析DFIG在电网电压对称骤升时的暂态特性,采用电动机惯例,忽略磁饱和现象后,DFIG在定子坐标系下的电压方程和磁链方程为:

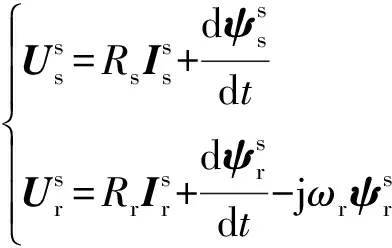
(1)

(2)

式中:U,I,ψ分别为电压、电流、磁链矢量;R和L为电阻和电感;Lm为定转子间的互感;ωr为转子旋转角速度;上标s和r分别表示定、转子参考坐标系;下标s和r分别表示定、转子分量。

根据式(1)、式(2)可得转子电压方程为:

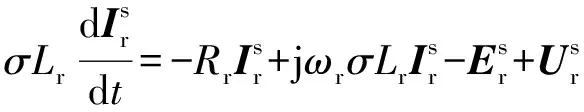
(3)

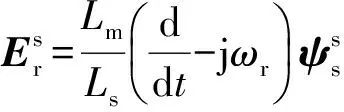
(4)

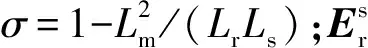
若t=0时,发生电网电压对称骤升故障,t=t1时故障切除,电压突变前后定子电压方程为:

(5)

式中:Us为电网电压幅值;d为电网电压骤升幅度;ω1为同步旋转角速度。

忽略定子电阻后,由式(1)可得:

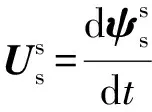
(6)

联立式(5)、式(6),定子磁链暂态全过程的表达式为:

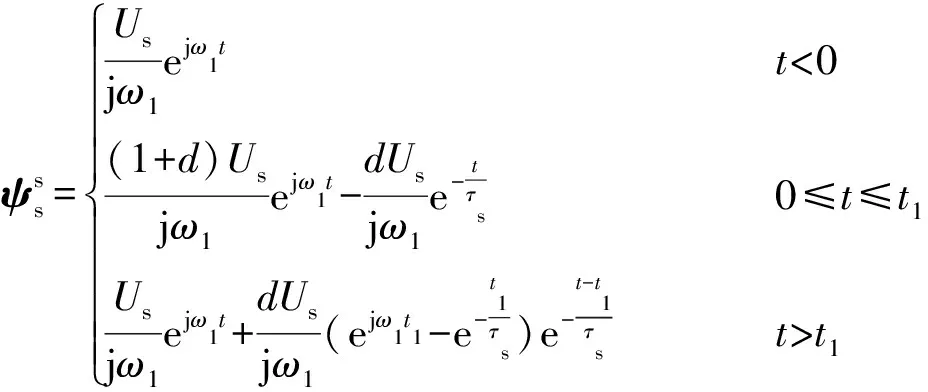
(7)

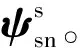
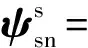
(8)

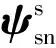
2　转子电流

将式(3)转换到转子旋转坐标系下为:

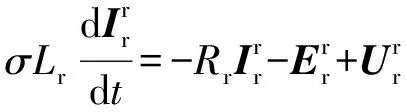
(9)

对于兆瓦级DFIG,Ls≫Rs,1/τs较其他项较小,可忽略不计。由式(4)和式(7)可得转子开路电压在转子旋转坐标系下为:

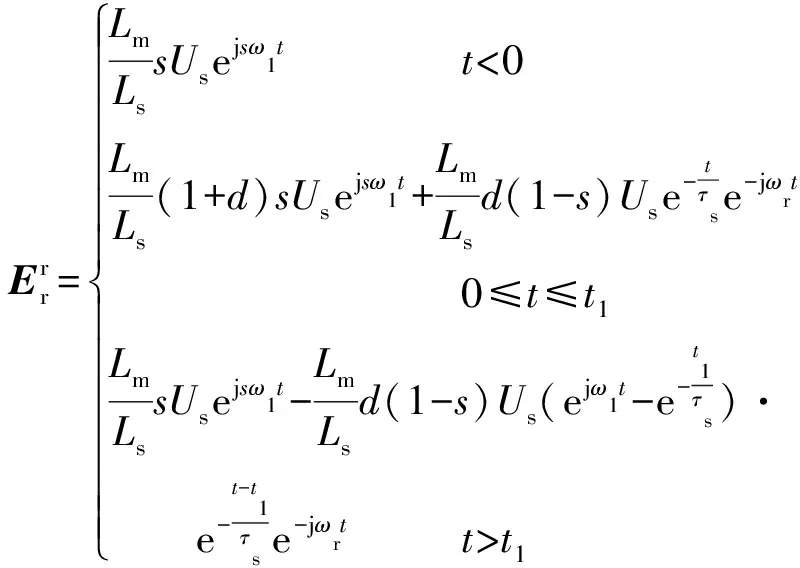
(10)

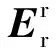
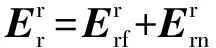
(11)

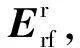
由式(9)、式(11)可知转子电流的动态方程为:

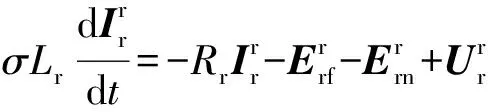
(12)

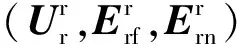
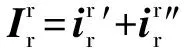
(13)

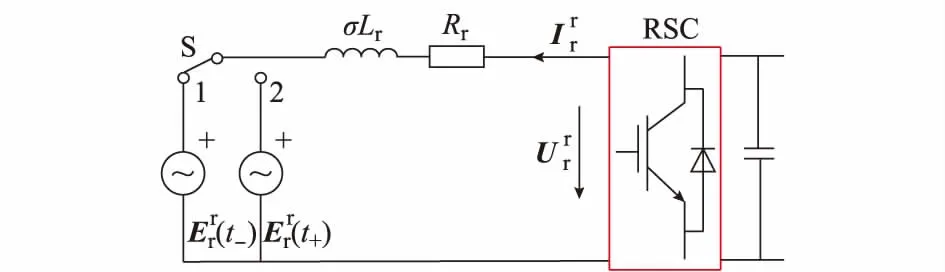
图1　转子回路换路过程等效电路Fig.1　Equivalent rotor circuit of DFIG during transition from one state to another

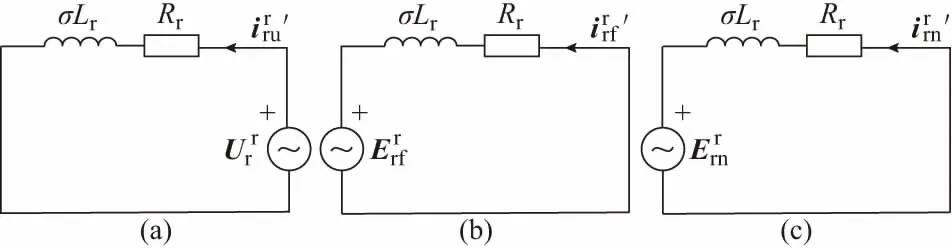
图2　故障过程中的等效转子电路Fig.2　Equivalent rotor circuit of DFIG during voltage fault

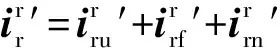
(14)

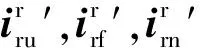
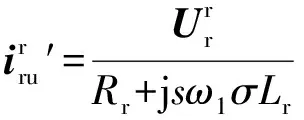
(15)

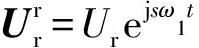
(16)

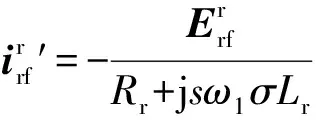
(17)

将式(10)中的稳态分量代入(17),令k=Lm/Ls得:

(18)

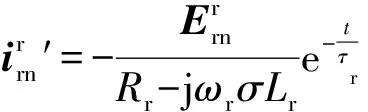
(19)

式中:τr为转子瞬态时间常数。

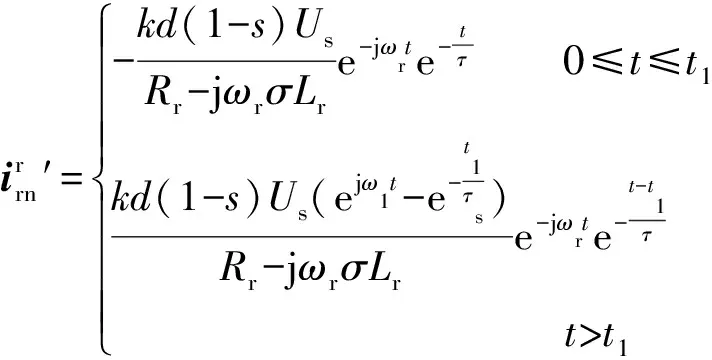
(20)

式中:τ=τsτr/(τs+τr)。

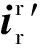
(21)

转子电流的直流分量可由下式确定:

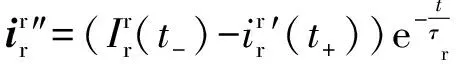
(22)

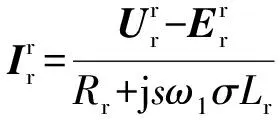
(23)

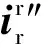
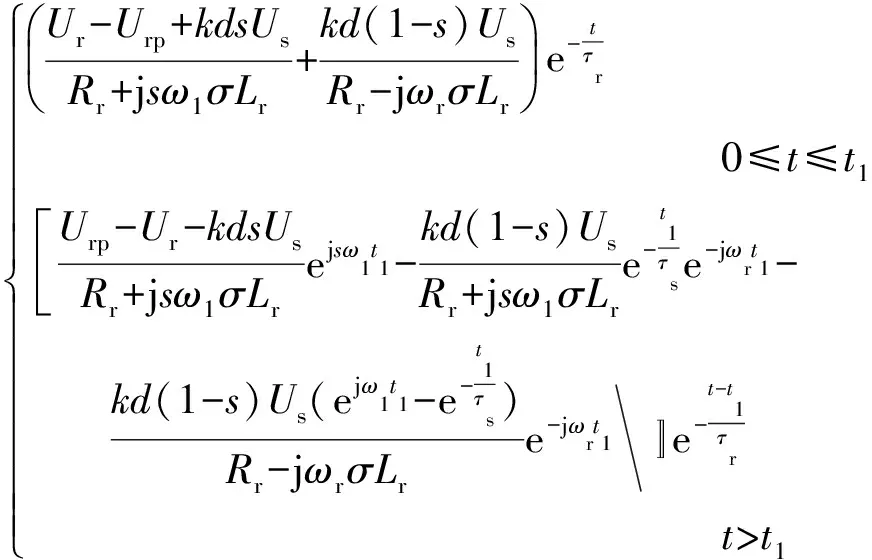
(24)

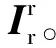
通过上述分析可知,故障过程中和故障切除后的转子电流由稳态交流分量、衰减的交流分量,以及直流分量组成,且电网电压故障切除后的转子电流要大于故障过程期间的转子电流。

转子电流的精确计算对HVRT控制策略制定有重要影响。例如:采用转子串电阻电路抑制转子过电流时,转子电流暂态过程分析不全面会使所选取的限流电阻偏小,无法抑制故障切除后的转子过电流。

3　转子串电阻电路分析

图3给出了含转子串电阻电路的DFIG结构，通过限流电阻来抑制HVRT中的转子过电流。图中：GSC为网侧换流器。

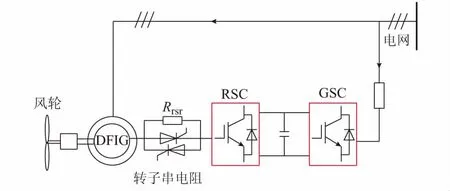
图3　含转子串电阻电路的DFIG结构Fig.3　DFIG structure of resistance circuit with rotor series

3.1　转子串电阻电路可行性分析

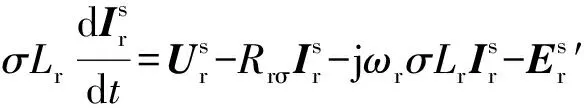
(25)

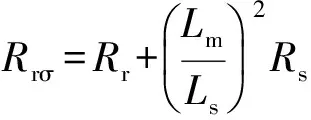
(26)

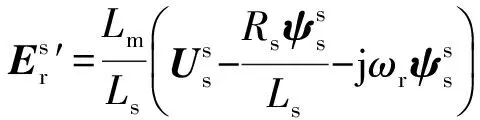
(27)

式中:Rrσ为转子瞬态电阻。

可见,增大Rr就能够增加Rrσ,以此抑制转子过电流。此外,随Rrσ增加,τr有所减小,使转子电流中暂态直流分量衰减速度加快,且运行期间无需封锁转子侧换流器,DFIG始终处于可控状态,解决了撬棒保护电路存在的电机失控问题。

3.2　限流电阻Rrsr阻值的确定

Rrsr阻值的确定首先要以高电压故障下转子电流可能出现的最大值为依据;其次,故障期间转子侧换流器仍处于工作状态,所以还需要考虑其所能承受的最大电压。

转子电流的精确计算对限流电阻Rrsr阻值的整定有重要影响,而现有文献均认为转子电流的最大值出现在故障发生期间,以此来对Rrsr进行整定。但通过上一节的分析可知,故障切除后,转子电流的最大值要大于故障发生期间。因此,在进行限流电阻阻值的整定时,要综合考虑全时间尺度下转子电流的最大值,否则会导致Rrsr整定偏小,无法对故障切除后的转子过电流进行抑制。

故障切除后的转子电流为:

(28)

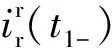
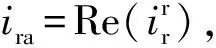
(29)

式中:β1=1/(σsω1τr);β2=1/(σωrτr)。

对上式取其最大值,可得

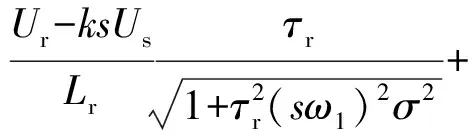
(30)

根据边界条件:

ira_max≤ir_lim

(31)

Ur≤URSC_lim

(32)

式中:ir_lim为转子电流的安全限值;URSC_lim为换流器电压的安全限值。

将式(31)、式(32)代入式(30)可求出转子暂态时间常数τr,根据τr=σLr/Rrσ,可得限流电阻Rrsr阻值为:

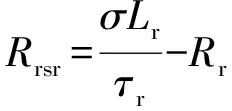
(33)

4　仿真分析

在MATLAB/Simulink仿真平台上搭建DFIG仿真模型,其中DFIG参数为:额定功率1.5 MW,定子额定线电压575 V,直流母线额定电压1 200 V,额定频率50 Hz,极对数为3,定子电阻0.007 06,转子电阻0.005,定子漏感0.171,转子漏感0.156,定转子间互感2.9,均为标幺值。故障前转速为1.2(标幺值),且故障期间转速恒定。

4.1　转子电流精度验证

为验证本文所给出转子电流解析式的正确性,分别对电网电压不同骤升程度时的转子电流进行仿真,图4给出了最大转子电流仿真和计算结果对比波形。

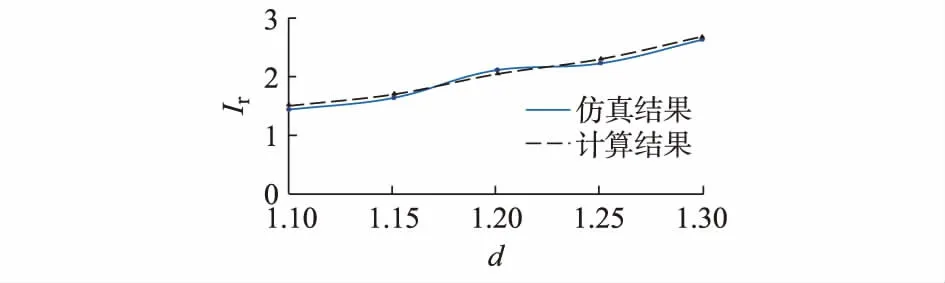
图4　最大转子电流仿真和计算结果Fig.4　Simulation and calculation result of maximum rotor current

计算结果和仿真结果基本吻合,采用本文所推导的转子电流解析式能够比较准确地描述DFIG转子电流。但仿真与计算结果仍存在小误差,这主要是由于理论分析中忽略了定子电阻且假设转速不变造成的。

此外,所采用的数学解析方法同时考虑了转子侧换流器输出和机端电压不同骤升程度对转子电流的影响,所得转子电流表达式更具一般性。

4.2　转子电流

为对比故障切除时间对转子电流的影响,附录A给出了2 s时电压对称骤升至1.3(标幺值),故障切除时间分别为2.02,2.03,2.43 s时的转子电流波形。

故障持续时间为0.02 s时,HVRT期间转子电流在安全限值2(标幺值)[20]以内,故障切除后,转子电流逐渐稳定至1(标幺值)。在转子电流上表现为全时间尺度下无转子过电流现象发生,无需采用转子串联电阻保护电路。故障持续时间为0.03 s时,HVRT期间转子电流在安全限值以内,故障切除后转子电流的最大值达到3.3(标幺值),远大于故障期间,出现转子过电流现象,此时有必要投入转子串电阻电路来对故障切除后的转子过电流限值。当故障持续时间为0.43 s时,HVRT期间和电网电压恢复后转子电流最大值相差不大。因为在电网电压恢复时,定子磁链已衰减至稳定值附近,反映到转子电流上表现为故障期间和故障切除后转子电流最大值相差不大。

4.3　不同Rrsr取值对HVRT效果分析

2 s时电网电压骤升至1.3(标幺值),2.11 s时故障切除,分别按照传统限流电阻整定方式下的Rrsr阻值0.06(标幺值)与本文所提方式下的Rrsr阻值0.08(标幺值)进行仿真,附录B给出了两种电阻整定方式下转子电流、直流母线电压、有功功率、无功功率的对比波形。同时,为更好地对比两种电阻整定方式下的仿真效果,表1给出了转子电流、直流母线电压、有功功率、无功功率峰值的详细数据。

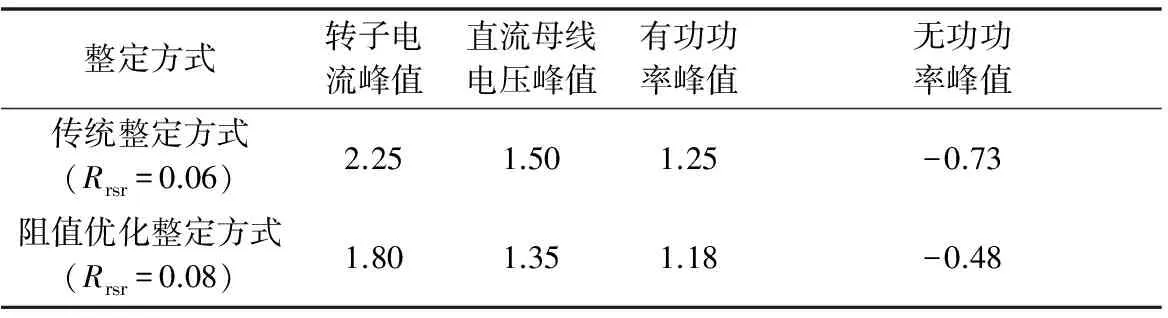
表1　不同整定方式下HVRT瞬态响应Table 1　HVRT transient response under different resistance strategies

可以看出,按照传统整定方法得到的Rrsr阻值使转子电流和直流母线电压的振荡幅度明显减小,对HVRT效果有一定的改进,但是故障切除后,转子电流超过其安全限值2(标幺值),对换流器的安全造成一定影响;此外,有功和无功功率的波动也较为明显。按照此方法整定的Rrsr偏小,无法抑制故障切除后的转子过电流;采用Rrsr阻值优化的方法,转子电流在全时间尺度下都处于安全限值以内,且直流母线电压、转子电流、有功功率、无功功率的瞬态响应较传统整定方式下更具优越性。可见,采用Rrsr阻值优化的方法更为合理。

5　结论

本文在对DFIG电磁暂态全过程分析的基础上,推导出电网电压对称骤升故障发生到切除及其后的转子电流表达式,并对Rrsr的整定方法进行优化,仿真结果验证了理论分析的正确性,得出如下结论。

1)转子电流全过程表达式同时考虑了换流器输出和机端电压不同骤升程度对转子电流的影响,且具有较高的精度。

2)揭示了故障持续时间对DFIG转子电流的影响。故障持续时间较短,且t1=(K+0.5)T时,故障切除后转子过电流现象明显。

3)传统Rrsr阻值整定方法只分析了HVRT期间转子电流的最大值,忽略了故障切除这一特殊时刻,使Rrsr阻值偏小,不能有效抑制故障切除后的转子过电流;Rrsr阻值优化方法综合考虑全时间尺度下转子电流的最大值,整定方法更加合理。

上述结论对DFIG的HVRT运行研究及控制策略的制定具有一定的指导意义。但本文仅对电网电压对称骤升故障下的转子电流进行了理论推导,今后将进一步完善电网电压不对称骤升故障下转子电流的理论分析。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 贾俊川,刘晋,张一工.电网电压故障时双馈异步发电机定子磁链的动态特性研究[J].中国电机工程学报,2011,31(3):90-96.

JIA Junchuan, LIU Jin, ZHANG Yigong. Dynamic characteristics of stator flux of doubly-fed induction generator during grid voltage fault[J]. Proceedings of the CSEE, 2011, 31(3): 90-96.

[2] OKEDU KENNETH E, MUYEEN S M, TAKAHASHI R, et al. Wind farms fault ride through using DFIG with new protection scheme[J]. IEEE Transactions on Sustainable Energy, 2012, 3(2): 242-254.

[3] WEISE B. Impact ofK-factor and active current reduction during fault-ride-through of generating units connected via voltage-sourced converters on power system stability[J]. IET Renewable Power Generation, 2015, 9(1): 25-36.

[4] 徐海亮,章玮,贺益康,等.双馈型风电机组低电压穿越技术要点及展望[J].电力系统自动化,2013,37(20):8-15.

XU Hailiang, ZHANG Wei, HE Yikang, et al. A review on low voltage ride-through technologies and prospect for DFIG wind turbines[J]. Automation of Electric Power Systems, 2013, 37(20): 8-15.

[5] LIU Xiaoge, XU Zhao, WONG K P. Recent advancement on technical requirements for grid integration of wind power[J]. Journal of Modern Power Systems and Clean Energy, 2013, 1(3): 216-222.

[6] 孟永庆,翁钰,王锡凡,等.双馈感应发电机暂态性能精确计算及Crowbar电路参数优化[J].电力系统自动化,2014,38(8):23-29.DOI:10.7500/AEPS20130818001.

MENG Yongqing, WENG Yu, WANG Xifan, et al. Accurate calculation of DFIG transient performance and parameters optimization of Crowbar circuit[J]. Automation of Electric Power Systems, 2014, 38(8): 23-29. DOI: 10.7500/AEPS20130818001.

[7] LI Ruiqi, GENG Hua, YANG Geng. Fault ride-through of renewable energy conversion systems during voltage recovery[J]. Journal of Modern Power Systems and Clean Energy, 2013, 37(4): 14-20.

[8] 翟佳俊,张步涵,谢光龙,等.基于撬棒保护的双馈风电机组三相对称短路电流特性[J].电力系统自动化,2013,37(3):18-23.

ZHAI Jiajun, ZHANG Buhan, XIE Guanglong, et al. Three-phase symmetrical short-circuit current characteristics analysis of wind turbine driven DFIG with crowbar protection[J]. Automation of Electric Power Systems, 2013, 37(3): 18-23.

[9] SUFFA F, SVENSSON J. Symmetrical and unsymmetrical short-circuit current of squirrel-cage and doubly-fed induction generators[J]. Automation of Electric Power Systems Research, 2011, 81(7): 1610-1681.

[10] 郑涛,魏占朋,李娟,等.计及撬棒保护的双馈风电机组不对称短路电流特性分析[J].电力系统保护与控制,2014,42(2):7-12.

ZHENG Tao, WEI Zhanpeng, LI Juan, et al. Unsymmetrical short circuit current analysis of doubly fed induction generators with crowbar protection[J]. Power System Protection and Control, 2014, 42(2): 7-12.

[11] 郑重,杨耕,耿华.电网故障下基于撬棒保护的双馈风电机组短路电流分析[J].电力自动化设备,2012,32(11):7-14.

ZHENG Zhong, YANG Geng, GENG Hua. Short-circuit current analysis for DFIG-based wind generation system with crowbar protection under grid faults[J]. Electric Power Automation Equipment, 2012, 32(11): 7-14.

[12] 徐殿国,王伟,陈宁.基于撬棒保护的双馈电机风电场低电压穿越动态特性分析[J].中国电机工程学报,2010,30(22):29-36.

XU Dianguo, WANG Wei, CHEN Ning. Dynamic characteristic analysis of doubly-fed induction generator low voltage ride-through based on Crowbar protection[J]. Proceedings of the CSEE, 2010, 30(22): 29-36.

[13] 凌禹.大型双馈风电机组故障穿越关键技术研究[D].上海:上海交通大学,2014.

[14] 熊小伏,欧阳金鑫.电网短路时双馈感应发电机转子电流的分析与计算[J].中国电机工程学报,2012,32(28):115-121.

XIONG Xiaofu, OUYANG Jinxin. Analysis and calculation of rotor currents for doubly-fed induction generators under short circuits in power grids[J]. Proceedings of the CSEE, 2012, 32(28): 115-121.

[15] 孔祥平,张哲,尹项根,等.计及励磁调节特性影响的双馈风力发电机组故障电流特性[J].电工技术学报,2014,29(4):256-265.

KONG Xiangping, ZHANG Zhe, YIN Xianggen, et al. Fault current characteristics of DFIG considering excitation and regulation characteristics[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 256-265.

[16] 李少林,王伟胜,王瑞明,等.双馈风电机组高电压穿越控制策略与试验[J].电力系统自动化,2016,40(16):76-82.DOI:10.7500/AEPS20160401005.

LI Shaolin, WANG Weisheng, WANG Ruiming, et al. Control strategy and experiment of high voltage ride through for DFIG-based wind turbines[J]. Automation of Electric Power Systems, 2016, 40(16): 76-82. DOI: 10.7500/AEPS20160401005.

[17] RAHIMI M, PARNIANI M. Transient performance improvement of wind turbines with doubly fed induction generators using nonlinear control strategy[J]. IEEE Transactions on Energy Conversion, 2010, 25(2): 514-525.

[18] 孟娜娜,孙丽玲.基于转子串电阻的双馈风电机组故障穿越方法研究[J].现代电力,2017,34(3):19-24.

MENG Nana, SUN Liling. Analysis of fault ride-through of doubly-fed wind power generator based on rotor series resistor[J]. Modern Electric Power, 2017, 34(3): 19-24.

[19] 张曼,姜惠兰.协调相邻风电场之间低电压穿越的综合保护方案[J].电网技术,2013,37(7):1983-1989.

ZHANG Man, JIANG Huilan. A comprehensive protection scheme for the LVRT coordination between neighboring wind farms[J]. Power System Technology, 2013, 37(7): 1983-1989.

[20] 凌禹,蔡旭.基于转子串电阻的双馈风电机组故障穿越技术[J].电力自动化设备,2014,34(8):25-30.

LING Yu, CAI Xu. Fault ride-through of DFIG wind turbine with rotor series resistor[J]. Electric Power Automation Equipment, 2014, 34(8): 25-30.

孙丽玲(1972—),女,博士,副教授,主要研究方向:大型电机的状态监测与故障诊断。E-mail： sll_ncepu@126.com

王艳娟(1992—),女,通信作者,硕士研究生,主要研究方向:双馈风力发电系统运行。E-mail: 734741309@qq.com