弱电网下考虑锁相环影响的并网逆变器改进控制方法

张学广, 付志超, 陈文佳, 徐殿国

(哈尔滨工业大学电气工程系, 黑龙江省哈尔滨市 150001)

0　引言

随着三相并网逆变器的应用日益广泛,其并网稳定问题目前受到普遍关注[1]。由于电网阻抗的存在,并网逆变器的控制系统与电网阻抗相互耦合,其滤波器引起的谐振、电网阻抗与逆变器控制系统的耦合作用,以及并联逆变器控制系统之间的耦合作用,都可能导致系统稳定性下降,产生振荡甚至失稳[2-4]。因此有必要研究并网逆变器不稳定产生原因及改进控制方法。

目前针对三相并网逆变器稳定性的研究,主要关注于逆变器系统中滤波器谐振和电流环设计,通常使用虚拟阻抗方法来提高系统稳定性[5-7]。文献[8]在LCL型并网逆变器电容电流反馈基础上,加入高通滤波器,等效在滤波电容两端并联RC阻尼器,消除传统阻尼器带来的相角滞后,提高谐波抑制能力。文献[9]在三相静止坐标系下,利用电网电压前馈,抵消电网背景谐波对逆变器电流的影响,同时基于在线电网阻抗测量方法,对并网逆变器进行自适应控制,实时调节锁相环带宽,提高系统稳定性。文献[10]分析了逆变器侧电流反馈 LCL 并网逆变器存在的问题,提出了一种适用于逆变器侧电流反馈并网逆变器的电网电压全前馈策略,完全消除了电网电压畸变对并网电流的影响。文献[11]通过阻抗分析法研究了弱电网条件下并网逆变器的稳定性,基于系统相角裕度动态补偿控制思路,提出了一种并网逆变器阻抗相角补偿策略。文献[12]介绍了目前虚拟阻抗的不同实施方式,对基于虚拟阻抗控制的电流源和电压源型变换器进行了系统的总结。

锁相环是目前三相并网装置中普遍采用的电网相位检测方法,锁相环的动态特性在不同并网条件下对系统稳定性的影响不容忽视。弱电网条件下,并网逆变器锁相环与电网阻抗之间存在很强的耦合现象[13]。文献[14]研究了锁相环与电网阻抗的耦合关系,提出随着电网阻抗的增加,锁相环与电网阻抗的耦合关系加剧,锁相环最大增益下降,系统稳定性降低。文献[15]考虑了锁相环的影响,利用多目标函数求解,设计并网变换器电流环控制器参数,使变换器的控制性能呈现更优异的鲁棒性和动静态响应特性。文献[16]分析了弱电网下锁相环对于并网逆变器稳定性的影响,提出并网逆变器与弱电网之间基于逆变器输出阻抗的级联稳定判据,结合相角裕度给出了锁相环参数的设计方法。

文献[14-16]均从控制器参数设计的角度提高并网逆变器稳定性。目前通过改变控制器结构提高并网逆变器稳定性的研究相对较少。因此,本文在同步旋转坐标系下建立了包括锁相环、电流环和滤波器等环节的三相并网逆变器阻抗模型,分析不同电网阻抗和锁相环带宽对三相并网逆变器稳定性的影响。利用阻抗模型中系统电压通过锁相环对控制电流的影响,提出一种改进的前馈控制方法来减小锁相环输出影响,前馈环节中包括系统电压和锁相环动态特性和滤波器等环节。

本文首先建立考虑锁相环影响的三相并网逆变器的阻抗模型;然后采用广义奈斯判据分析不同条件下系统稳定性,提出考虑锁相环影响的逆变器稳定性改进控制方法,增强并网逆变器弱电网适应性。最后通过实验结果证明了本文理论分析的正确性。

1　三相并网逆变器输出阻抗建模

1.1　三相并网逆变器

图1为三相并网逆变器的结构框图。图中:Udc为直流电压;idc为直流侧电流;S1至S6为6个反并联二极管的自关断器件;ia,ib,ic为逆变器侧电流;L为逆变器侧滤波电感;R为电感L上寄生电阻;Cf为滤波电容;Lg为电网电感;Rg为电感Lg上电阻;Uca,Ucb,Ucc为锁相环采集三相电压;ea,eb,ec为电网三相电压;iga,igb,igc为三相并网电流;θPLL为锁相环相角;Gdel为等效延时矩阵。三相并网逆变器采用电网电压定向矢量控制方式,电流环使用比例—积分(PI)控制器,电流环表达式为:

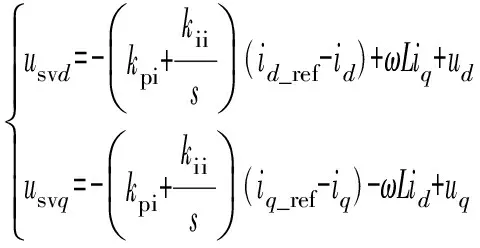
(1)

式中:ω为工频角速度;kpi和kii分别为电流环比例系数和积分系数;id,iq,id_ref,iq_ref分别为dq坐标系下d轴并网电流、q轴并网电流、d轴并网电流参考值、q轴并网电流参考值;ud,ud,usvd,usvq分别为dq坐标系下d轴并网电压、q轴并网电压、电流环d轴输出电压、电流环q轴输出电压。

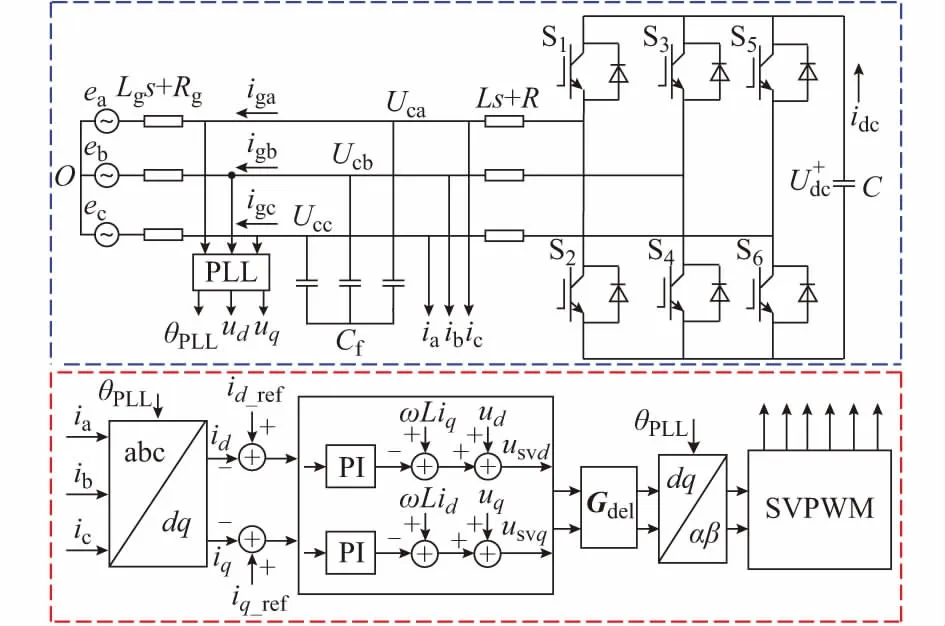
图1　三相并网逆变器结构框图Fig.1　Block diagram of three-phase grid-connected inverter

1.2　并网逆变器输出阻抗推导

针对并网逆变器稳定性分析,阻抗建模是一种广泛使用的方法[17-19]。阻抗分析法通过建立并网逆变器输出阻抗的二阶矩阵,利用广义奈斯判据对逆变器稳定性进行判断[20-21]。本文使用阻抗分析法,推导同步旋转坐标系下并网逆变器交流侧阻抗模型,模型结果如附录A图A1所示。

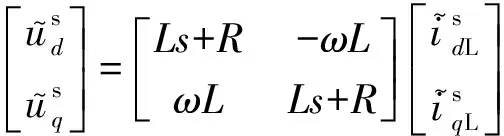
(2)

由此得到逆变器开环阻抗为:

(3)

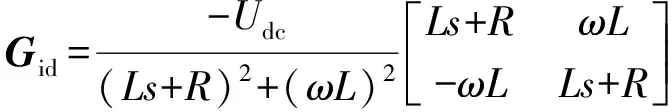
(4)

并网逆变器通常使用锁相环来获取电网同步信息,其动态特性会影响系统稳定性。为了分析锁相环对系统可能造成的影响,在小信号模型中加入锁相环,进而分析系统的稳定性。

系统和控制器dq坐标系如附录A图A2所示。在稳定状态下,系统和控制器的dq坐标轴应该重合。若电网电压中存在扰动,由于锁相环动态特性,两个坐标系存在一个角度差Δθ,影响系统稳定性。系统dq坐标轴向量到控制器dq坐标轴向量的传递函数可用旋转矩阵TΔθ表示:

(5)

因此有

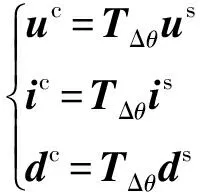
(6)

式中:上标s表示该变量在系统dq坐标系下,上标c表示该变量在控制器dq坐标系下;uc和us分别为控制器dq坐标系下和系统dq坐标系下的电压小信号向量;ic和is分别为控制器dq坐标系下和系统dq坐标系下的电流小信号向量;dc和ds分别为控制器dq坐标系下和系统dq坐标系下的电流小信号向量。

由锁相环平均模型可知,电网dq坐标系和控制器dq坐标系下的稳态关系如下:

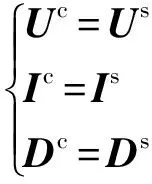
(7)

式中:Uc和Us分别为控制器dq坐标系下和系统dq坐标系下的电压稳态向量;Ic和Is分别为控制器dq坐标系下和系统dq坐标系下的电流稳态向量;Dc和Ds分别为控制器dq坐标系下和系统dq坐标系下的占空比稳态向量。

式(7)表明系统坐标系和控制器坐标系的向量相角差为0,再由旋转矩阵TΔθ得到:

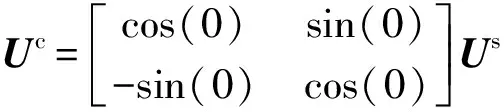
(8)

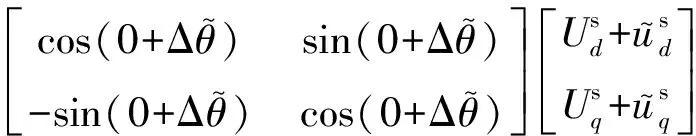
(9)

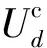
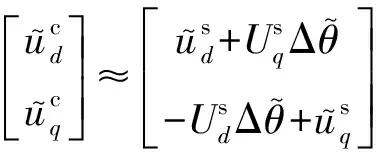
(10)

锁相环输出为:

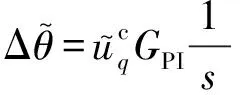
(11)

式中:GPI=kppll+kipll/s,其中kppll和kipll分别为锁相环的比例系数和积分系数。

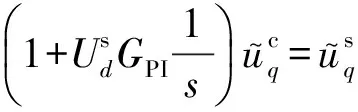
(12)

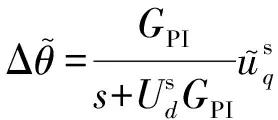
(13)

定义GPLL为:

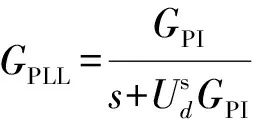
(14)

由此得到:

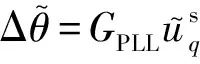
(15)

由式(10)和式(15)求得:

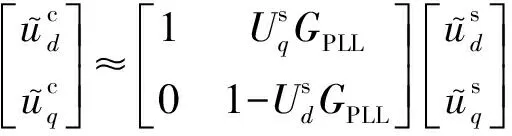
(16)

(17)

同理得到:

(18)

(19)

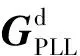
考虑电流环、锁相环及滤波器环节,得到三相并网逆变器阻抗模型框图如图2所示。图中:Gdel为考虑延时的传递矩阵,Gdec为解耦项矩阵,Gci为电流环PI控制矩阵。

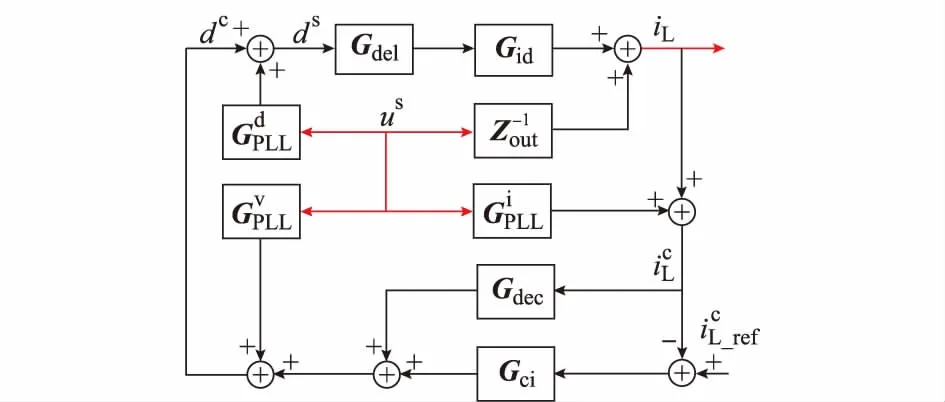
图2　并网逆变器阻抗模型框图Fig.2　Block diagram of grid-connected inverter output impedance model

Gdel,Gdec,Gci的表达式为:

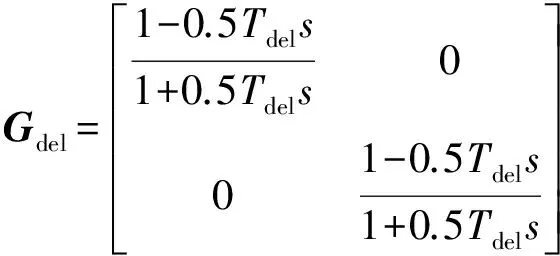
(20)

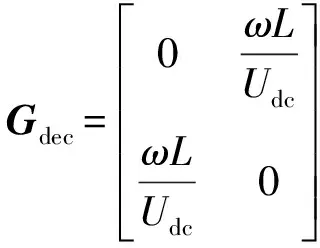
(21)

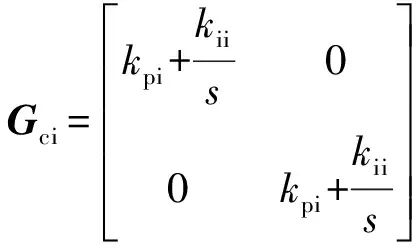
(22)

式中:Tdel=1/fsw,其中fsw为开关频率。

由此得到系统闭环输出阻抗为:

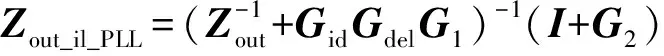
(23)

其中

电网阻抗矩阵Zg由电网阻抗Lg与滤波电容Cf并网值构成,由广义奈斯判据可知:

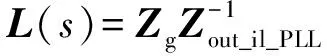
(24)

式(24)满足广义奈斯判据则系统稳定,否则不稳定。

2　电网阻抗和锁相环带宽对系统稳定性的影响分析

2.1　电网阻抗对系统稳定性的影响

电网阻抗与并网逆变器控制系统的交互作用对系统稳定性有一定影响。本节根据前文建立的三相逆变器阻抗模型,应用广义奈斯判据分析不同电网阻抗条件下系统稳定性。

系统参数如附录A表A1所示,其中Lg=4 mH时对应线路短路比(SCR)为12.8,Lg=16 mH时对应线路短路比为3.2。由文献[22]中的锁相环带宽定义,得到表A1中对应的锁相环PI参数设置。锁相环带宽为100 Hz,线路短路比为12.8时对应的奈奎斯特曲线如附录A图A3所示。附录A图A3(a)描绘系统奈奎斯特曲线的整体轮廓图,为清晰地描述奈奎斯特曲线与复平面(-1,j0)点的环绕关系,本文后续奈奎斯特曲线均使用局部放大图。

由附录A图A3可知,两条奈氏曲线均未包围(-1,j0)点,系统处于稳定状态。在此条件下,将电网侧阻抗增大至16 mH,得到如附录A图A4所示的奈奎斯特曲线。图中奈奎斯特曲线包围(-1,j0)点,表明系统处于不稳定状态。

由附录A图A3和图A4可知,电网阻抗的增加会导致电网与逆变器控制系统交互作用增强,系统稳定性降低。

2.2　锁相环带宽对系统稳定性的影响

在弱电网条件下,锁相环带宽的增加,会影响锁相环与电网阻抗的耦合性,不利于系统稳定。本节在线路短路比为3.2的条件下,通过奈奎斯特曲线,分析不同锁相环带宽对系统稳定性影响。

附录A图A5(a)表示锁相环带宽为13 Hz时对应的奈奎斯特曲线,曲线未包围(-1,j0)点,系统处于稳定状态。锁相环带宽为100 Hz时对应的奈奎斯特曲线如附录A图A5(b)所示,图中曲线包围(-1,j0)点,表示系统处于不稳定状态。对比附录A图A5(a)和(b)中的奈奎斯特曲线可知,在弱电网条件下,锁相环带宽的增加使电网阻抗与锁相环耦合性增强,降低系统稳定性,甚至造成失稳。

3　考虑锁相环影响的并网逆变器改进控制方法

由2.2节分析可知,电网阻抗和锁相环带宽均会影响系统稳定性。本文从提高并网逆变器弱电网适应性角度,提出一种考虑锁相环影响的并网逆变器改进控制方法,在弱电网条件下,减小锁相环输出误差,使并网逆变器在锁相环高带宽条件下稳定运行。在实施所提方案时,并未改变锁相环结构和参数,因此在加入所提方案前后锁相环带宽不变。

3.1　考虑锁相环影响的并网逆变器稳定性提高方法

由于锁相环的动态特性,系统电压对控制电流产生影响,降低了系统稳定性。本文基于电压前馈思想,提出一种并网逆变器改进控制方法,降低系统电压通过锁相环对控制电流的影响。控制方法的框图如图3所示。

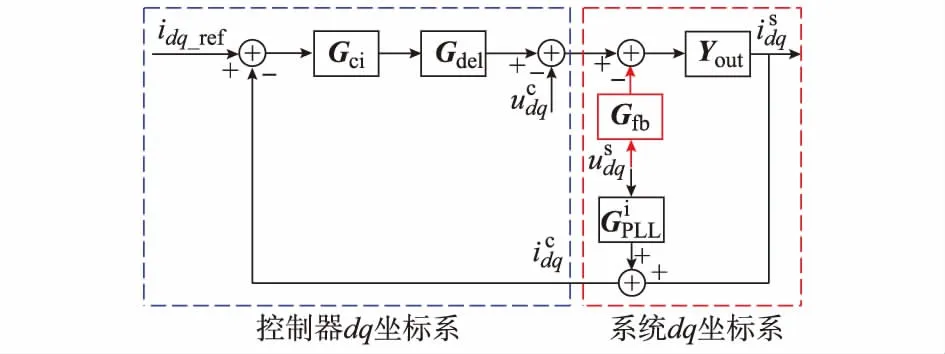
图3　所提方案电流环控制框图Fig.3　Control diagram of current loop with proposed strategy

图3中Gfb表示用以减小系统电压通过锁相环对控制电流影响的前馈项,其表达式为:

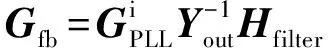
(25)

理论分析中的前馈电压为系统dq坐标系下公共耦合点电压,而实际使用的是控制器dq坐标系下公共耦合点电压。因此可根据系统电压和控制器坐标系电压关系,将图3中前馈电压替换为控制器坐标系电压,得到实际前馈项,即

(26)

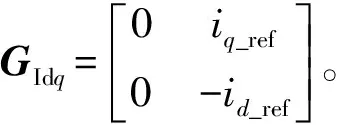
由式(26)可知,实际前馈项矩阵特点决定实际前馈电压仅有uq,得到所提方案实际电流环控制器表达式为:

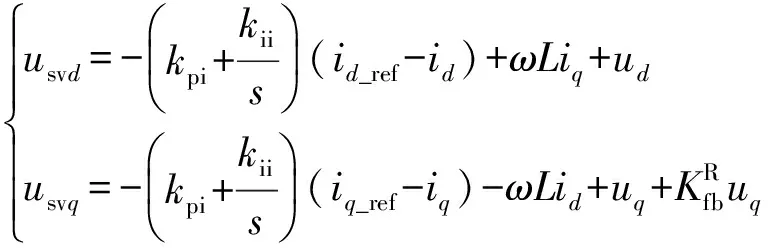
(27)

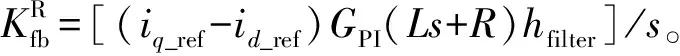
3.2　所提方法稳定性分析

根据所提方案电流环,结合前文建立的并网逆变器阻抗模型,得到所提方案并网逆变器阻抗模型框图,如图4所示。

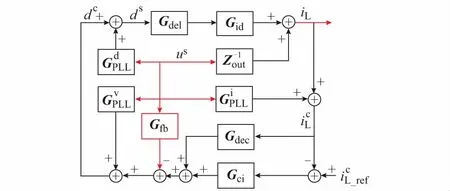
图4　所提方案并网逆变器阻抗模型框图Fig.4　Block diagram of impedance model of connected inverter in proposed strategy

系统参数见附录A表A1,其中线路短路比为3.2,锁相环带宽为100 Hz,得到加入所提方案前后的奈奎斯特曲线如图5所示。

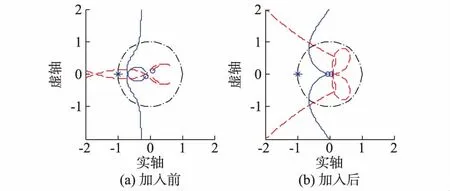
图5　加入所提方案前后的奈奎斯特曲线Fig.5　Nyquist curves with and without proposed strategy

图5(a)表示加入所提方案前系统的奈奎斯特曲线,曲线包围(-1,j0)点,系统处于不稳定状态。图5(b)表示加入所提方案后系统的奈奎斯特曲线,曲线不再包围(-1,j0)点,系统处于稳定状态。对比加入所提方案前后的奈奎斯特曲线可知,所提方案可以减小锁相环与电网阻抗的耦合性,提高并网逆变器弱电网稳定性。

附录A图A7表示线路短路比为3.2、锁相环带宽为100 Hz条件下,加入所提方案前后并网逆变器qq轴阻抗波特图。对比附录A图A7中波特图可知,在加入所提方案后,qq轴负阻抗频率范围明显减小,系统稳定性提高,分析结果进一步验证了所提方法有效性。

4　实验验证

为验证上述所提方法的正确性,本文采用一台三相并网逆变器进行实验。逆变器模块为英飞凌的FF1400R12IP4,主控数字信号处理器(DSP)芯片采用TI公司的TMS320F2812。为实验验证方便,在逆变器与公共电网之间串联不同电感来模拟不同电网阻抗接入条件。实验参数见附录A表A1。

附录B图B1表示锁相环带宽为100 Hz时不同电网阻抗条件下的实验波形。附录B图B1(a)为电网电感4 mH时对应的并网逆变器输出电流与并网点电压波形。由附录B图B1(a)可知,电网阻抗较小时,系统稳定。附录B图B1(b)表示电网电感为16 mH时逆变器输出电流和并网点电压波形,图中电压、电流波形均存在畸变。对比附录B图B1(a)和(b)波形可知,电网阻抗的增大使锁相环与电网阻抗的耦合性增强,导致系统失稳。

附录B图B2(a)为电网电感4 mH时逆变器输出电流快速傅里叶变换(FFT)分析图,图中无谐振峰,系统处于稳定状态。附录B图B2(b)为电网电感16 mH时逆变器输出电流FFT分析图,图中出现35 Hz和135 Hz谐振峰,系统不稳定。

附录B图B3表示电网电感为16 mH、锁相环带宽为13 Hz时,逆变器输出电流和并网点电压波形。对比附录B图B1(b)和附录B图B3可知,在弱电网条件下,减小锁相环带宽可提高系统稳定性。

图6所示电网阻抗为16 mH、锁相环带宽为100 Hz时加入所提方案前后实验波形。图6(a)所示为加入所提方案前的实验波形,此时电压、电流波形产生畸变,系统不稳定。图6(b)所示为加入所提方案后的实验波形,图中电压、电流波形无畸变,系统稳定。对比图6(a)和(b)可知,加入所提方案使锁相环与电网阻抗耦合性降低,锁相环输出误差减小,系统稳定性提高。

通过附录B图B3与图6(a)对比可知,弱电网条件下,较高的锁相环带宽会导致电网阻抗与锁相环耦合增强,引起系统不稳定。

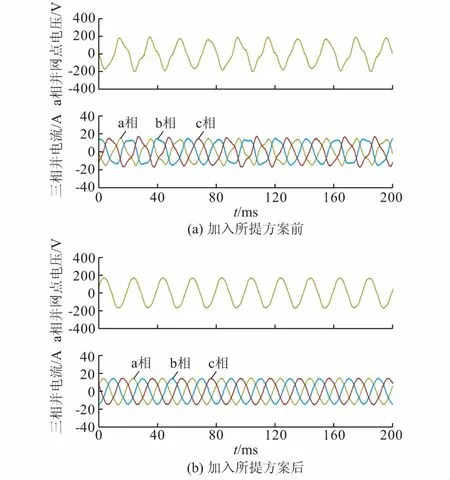
图6　加入所提方案前后并网逆变器实验波形Fig.6　Experimental waveforms of grid-connected inverter with and without proposed strategy

附录B图B4表示电网阻抗为16 mH,加入所提方案前后的动态实验波形。附录B图B4(a)所示为加入所提方案前,锁相环带宽为13 Hz时,d轴电流动态实验波形。附录B图B4(b)所示为加入所提方案后,锁相环带宽为100 Hz时,d轴电流动态实验波形。对比附录B图B4(a)和(b)可知,加入所提方案后,对系统动态性能影响不大。

以上实验结果表明,电网阻抗和锁相环带宽的增加会降低系统稳定性。在锁相环带宽较高的弱电网条件下,加入所提方法能够明显改善逆变器输出电流波形,提高系统稳定性,实验结果验证了理论分析的正确性。

5　结语

本文基于阻抗分析法,建立了考虑锁相环影响的三相并网逆变器输出阻抗模型。文中分析结果表明,电网阻抗和锁相环带宽的增加会导致锁相环与电网阻抗耦合性增强,降低系统稳定性。本文根据阻抗模型中系统电压经过锁相环对控制电流的影响,利用系统电压前馈减小锁相环输出误差,提高并网逆变器弱电网适应性。理论分析和实验结果均验证了所提方案的正确性。本文重点针对锁相环与电网阻抗的耦合性问题进行分析,下一步工作将进一步研究弱电网下控制器与锁相环耦合性问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] MARCO L, REMUS T, FREDE B. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J]. IEEE Transactions on Power Electronics, 2006, 21(1): 263-272.

[2] 杨淑英,张兴,张崇巍,等.LCL滤波电压源并网逆变器多环控制策略设计[J].电力系统自动化,2011,35(5):66-70.

YANG Shuying, ZHANG Xing, ZHANG Chongwei, et al. Strategy design of multiple feedback loop control for grid-connected voltage source inverter with LCL filter[J].Automation of Electric Power Systems, 2011, 35(5): 66-70.

[3] 陈新,张旸,王赟程.基于阻抗分析法研究光伏并网逆变器与电网的动态交互影响[J].中国电机工程学报,2014,34(27):4559-4567.

CHEN Xin, ZHANG Yang, WANG Yuncheng. A study of dynamic interaction between PV grid-connected inverters and grid based on the impedance analysis method[J]. Proceedings of the CSEE, 2014, 34(27): 4559-4567.

[4] WANG Xiongfei, FREDE B, WU Weimin. Modeling and analysis of harmonic stability in an AC power-electronics-based power system[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6421-6432.

[5] 殷进军,刘邦银,段善旭.LCL滤波并网逆变器双环控制参数设计与优化[J].电力系统自动化,2013,37(9):123-128.

YIN Jinjun, LIU Bangyin, DUAN Shanxu. Parameters design and optimization of dual-loop controller for grid-connected inverters with LCL filters[J]. Automation of Electric Power Systems, 2013, 37(9): 123-128.

[6] TANG Yi, POH C L, WANG Peng, et al. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1433-1443.

[7] 杨东升,阮新波,吴恒.提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法[J].中国电机工程学报,2014,35(15):2327-2335.

YANG Dongsheng, RUAN Xinbo, WU Heng. A virtual impedance method to improve the performance of LCL-type grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2014, 35(15): 2327-2335.

[8] WANG Xiongfei, FREDE B, POH C L. Virtual RC damping of LCL-filtered voltage source converters with extended selective harmonic compensation[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 4726-4737.

[9] MAURICIO C, SUN Jian. Adaptive control of grid-connected inverters based on online grid impedance measurements[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 516-523.

[10] 吴云亚,谢少军,阚加荣,等.逆变器侧电流反馈的LCL并网逆变器电网电压前馈控制策略[J].中国电机工程学报,2013,33(6):54-60.

WU Yunya, XIE Shaojun, KAN Jiarong, et al. A full grid voltage feed-forward control strategy with inverter-side current feedback for LCL grid-connected inverters[J]. Proceedings of the CSEE, 2013, 33(6): 54-60.

[11] CHEN Xin, ZHANG Yang, WANG Shanshan, et al. Impedance-phased dynamic control method for grid-connected inverters in a weak grid[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 274-283.

[12] WANG Xiongfei, LI Yunwei, FREDE B, et al. Virtual-impedance-based control for voltage-source and current-source converters[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7019-7037.

[13] DONG D, BO W, DUSHAN B, et al. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 310-321.

[14] JENNY Z, DING Hui, FAN Shengtao, et al. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2287-2296.

[15] 周诗颖,邹旭东,童力,等.考虑锁相环影响的LCL型并网变换器电流环控制器参数设计[J].中国电机工程学报,2016,36(4):1075-1089.

ZHOU Shiying, ZOU Xudong, TONG Li, et al. Design of LCL-type grid-connected converter current loop controller parameters considering effects of phase locked loops[J]. Proceedings of the CSEE, 2016, 36(4): 1075-1089.

[16] 吴恒,阮新波,杨东升.弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J].中国电机工程学报,2014,34(30):5259-5268.

WU Heng, RUAN Xinbo, YANG Dongsheng. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE, 2014, 34(30): 5259-5268.

[17] LENNART H, MASSIMO B, STEFAN L. Input-admittance calculation and shaping for controlled voltage-source converters[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3323-3334.

[18] BO WEN, DUSHAN B, ROLANDO B, et al. Analysis ofD-Qsmall-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.

[19] 李小强,伍小杰,耿乙文,等.感性电网阻抗下三相光伏逆变器稳定性分析[J].中国电机工程学报,2014,34(28):2906-2916.

LI Xiaoqiang, WU Xiaojie, GENG Yiwen, et al. Stability analysis of three-phase PV inverter under inductive grid impedance condition[J]. Proceedings of the CSEE, 2014, 34(28): 2906-2916.

[20] SUN J. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.

[21] 刘增,刘进军.带变流器负载的三相交流电源系统稳定性判据的研究[J].中国电机工程学报,2012,32(25):143-148.

LIU Zeng, LIU Jinjun. Stability criterion for three-phase AC power systems with converter load[J]. Proceedings of the CSEE, 2012, 32(25): 143-148.

[22] WANG Xiongfei, HARNEFORS L, BLAABJERG F. Unified impedance model of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1775-1787.

张学广(1981—),男,通信作者,博士,副教授,博士生导师,主要研究方向:风力发电技术和大功率电力电子技术。E-mail： zxghit@126.com

付志超(1992—),男,硕士研究生,主要研究方向:并网逆变器建模及稳定性分析。E-mail: fzcsd92@163.com

陈文佳(1993—),男,硕士研究生,主要研究方向:并网逆变器稳定性分析。E-mail: chenwj_hit@126.com