带负载阻抗角反馈的主动频移孤岛检测技术

唐忠廷, 粟　梅, 刘　尧, 韩　华, 王　辉, 李　鑫

(1. 中南大学信息科学与工程学院, 湖南省长沙市410083; 2. 广东电网有限责任公司珠海供电局, 广东省珠海市 519000)

0　引言

作为可再生能源的主要载体,分布式光伏并网发电系统为解决能源短缺和环境污染问题提供了新的途径,给大电网注入了新的活力,同时也带来了新的挑战,其中最为严重的就是孤岛问题。孤岛是一个没有调节控制能力的电力系统,存在潜在的安全隐患,可能由于发电与供电的不平衡及电压和频率的过大偏移而损坏发电或用电设备。分布式并网发电系统必须具有良好的反孤岛能力,在孤岛形成时迅速成功地检测到孤岛,及时消除孤岛的危害[1-2]。

目前,分布式发电系统孤岛检测方法一般分为远程检测法和本地检测法[3-4]。其中,基于远程通信设备的远程检测法成本高、可靠性低,一般不常用。因此,基于逆变器的分布式并网发电系统孤岛检测常采用本地检测法。本地检测法可分为被动式和主动式两类。其中,主动移频(AFD)[3]是一种较好的主动式检测方法,具有无须添加任何外部设备和孤岛检测成功率高等特点。但是,由于AFD是通过对系统注入一定的扰动后检测系统输出电压是否超过设定阈值来判断孤岛,扰动的大小将影响系统的孤岛检测准确度和系统的电能质量。而一些传统的主动式孤岛检测法如带正反馈的主动式频率偏移(active frequency drift with positive feedback,AFDPF)孤岛检测法[4]和滑动频率偏移(slip-mode frequency shifting,SMS)孤岛检测法[5]均无法兼顾孤岛检测的准确度和电能质量,存在检测盲区。为此,国内外学者提出了多种改进的算法[6-13]。文献[6]提出了一种改进的AFD孤岛检测技术,通过对电流施加可变的截断系数(从0递增到指定截断系数cf值)扰动,达到减小并网电流畸变率的目的,但是有些扰动量相对较小,使得孤岛检测时间稍长,甚至导致检测失败。文献[7]提出一种带电压频率正反馈的AFD式孤岛检测方法,以改变一个周期内部分电流幅值的方式,提升检测速度的同时达到减小并网电流谐波畸变率的目的,但是其参数设置依然不能平衡检测精度与电能质量之间的矛盾。文献[10-12]通过向参考电流注入低频扰动,在电网故障时检测公共点频率变化的速度来判定孤岛,虽然可以保证并网电能质量,但是影响了逆变器的有功功率输出值。

综合分析各种AFDPF孤岛检测法,检测失败通常是负载相位角随频率变化引起的[14]。随着并/离网逆变器技术的大力发展,其孤岛模式分为计划性孤岛和非计划性孤岛,其中非计划性孤岛需要满足国家标准[15-16]。在并/离网模型逆变器中,负载阻抗角成为了一个可知量。因此,本文以负载阻抗角可以实时检测为前提,提出带负载阻抗角反馈的主动频移孤岛检测技术(active frequency drift with load impedance angle feedback,AFDLIA),在保证电能质量的前提下,消除了孤岛检测盲区,并较好地解决了系统非线性因素引起的谐波畸变问题。仿真和实验均验证了所提方法的有效性。

1　传统主动频移孤岛检测技术的原理

AFD检测技术的原理是将有轻微失真的逆变器电流注入大电网中,当孤岛发生,公共点电压频率偏移超过阈值,系统判定孤岛并实施保护[14]。对于单相逆变器,AFD检测技术采用轻微失真的逆变器输出电流有两种方式:频率向上偏移和向下偏移。因传统负载多以感性为主,因此大多数的文献都以频率向上偏移为例进行讨论。本文以向上偏移的频率扰动为例进行傅里叶变换(FFT)分析,阐述AFD孤岛检测的原理。

分布式并网逆变器通过锁相环得到公共点电压频率和幅值,以频率和幅值是否越过阈值来判断是否发生孤岛。文献[17]中叙述了单相锁相环的机理,即通过滤除两次以上的高次谐波获得电网电压相位角和基频值。本文主要利用FFT分析AFD检测技术中电流扰动对公共点电压基频产生的影响。为了直观地反映电流扰动对公共点电压的影响,本文以纯电阻负载为例来进行分析,失真的逆变器输出电流的特性无偏差的传递到公共点电压。

AFD检测技术采用频率向上偏移的扰动,逆变器的给定参考电流作归一化处理,定义为:

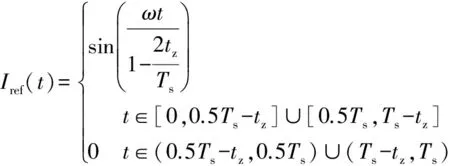
(1)

式中:tz为图1(a)中逆变器参考电流的斩波时间,表征了AFD孤岛检测技术所施加扰动的大小;ω为电网标准频率;Ts是参考电流的周期。

在纯电阻负载条件下,归一化公共点电压为:

(2)

为求取畸变后的公共点电压基频值,对单个周期的电压无限延拓后进行FFT分析,将图1(a)向右平移tz/2得到图1(b),一个中心对称的波形图FFT序列中只含奇次谐波,不含偶次谐波。

对该波形进行傅里叶分析,即

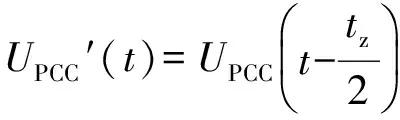
(3)

(4)

UPCC′(t)=U0′+(Ua1′cosωt+Ub1′sinωt)=

U0′+Ub1′sinωt

(5)

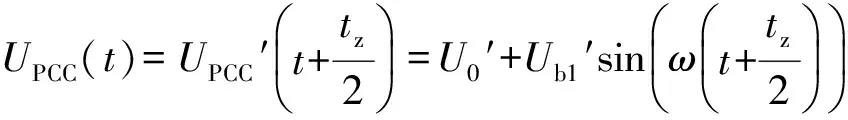
(6)

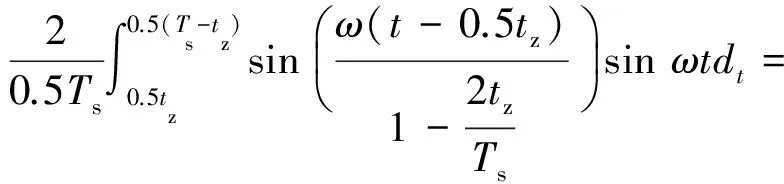
(7)

tz是一个很小的值,由等价无穷小原理可得:

(8)

Ub1′只有一个非常接近1的值,因此公共点电压幅值不会越过电压幅值的阈值。

基于单相锁相环锁基频的特性,锁相环对公共点电压锁相后的波形为图1(b)中的虚线波形。由于图1(b)是由图1(a)向右平移了tz/2时刻所得,实际锁相的零时刻为图1(b)中的tz/2时刻,因此在电网发生故障的第一个半周波,锁相得到的公共点电压频率为ω1=2π/(Ts-tz)。逆变器的下一个半周波电流扰动在频率为ω1的基础上施加,公共点电压频率继续偏移,其中Ts1=2π/ω1。因此,公共点电压将会以每半个周期移相πtz/Tsn的速度使得频率向上偏移直到频率超过阈值检测出孤岛。

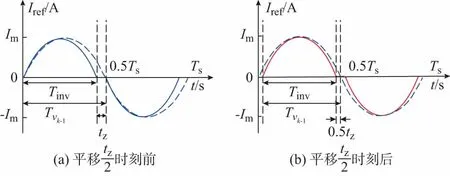
图1　AFD的参考给定电流波形Fig.1　Reference current waveforms of AFD

2　负载特性对孤岛检测的影响

负载的类型多种多样,孤岛检测技术中最挑剔的负载类型为RLC并联负载。其阻抗角为:

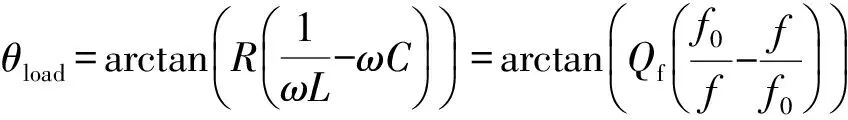
(9)

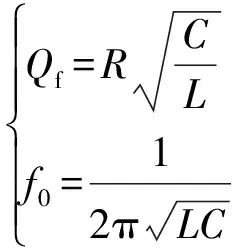
(10)

式中:Qf为负载的品质因数;f0为负载的谐振频率。

由式(9)可以看出,负载阻抗角与负载的电阻、电感、电容(决定品质因数)和频率有关系。品质因数越高对于孤岛检测技术的要求越是苛刻[15-16]。图2是RLC负载特性与频率的关系,ω0是负载的谐振频率。由图2可知,对于谐振频率是ω0的负载,当频率相对于ω0向上偏移时,负载阻抗角为负,呈容性;当频率相对于ω0向下偏移时,负载阻抗角为正,呈感性。

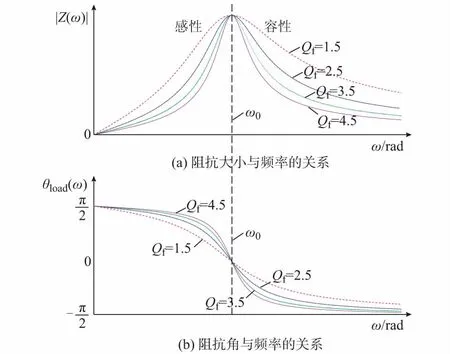
图2　RLC负载特性与频率的关系Fig.2　Load characteristics with different frequencies

因此,就单台逆变器而言,负载分为4种情况,即纯电阻负载、容性负载、感性负载、电网电压频率谐振负载[18]。当注入扰动产生的相位偏移与负载阻抗角相抵消时,AFD检测技术失败。纯电阻负载可以将电流频率偏移全部传递到公共点电压;感性负载时,电压超前电流,易使得采用向下扰动偏移的AFD检测技术失败;容性负载时,电压滞后电流,易使得采用向上扰动偏移的AFD检测技术失败。但是当负载谐振频率等于电网电压频率,电网故障时负载呈阻性,本周期AFD检测技术对频率的扰动会被完全传递,使频率升高(降低),偏离谐振频率的负载呈容(感)性,AFD检测技术对频率的扰动效应会受到负载相位角的阻碍,使得频率偏移速度减慢；严重的,扰动与负载相位角的作用相抵消,频率不再偏移无法越过阈值,孤岛检测失败。因此,对在电网电压频率谐振的负载,断网后新稳态满足的条件为:

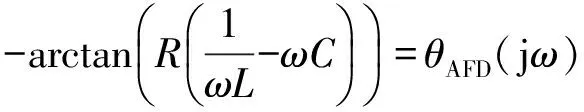
(11)

式中:θAFD(jω)是由AFD检测方法产生的相位偏移。

AFD检测技术中对并网电流注入扰动的大小是固定的,且扰动大,谐波畸变率大;扰动小,孤岛检测的准确度小。因此,有学者提出扰动随频率偏移变化的AFDPF检测技术[14],保留AFD检测技术的固定截断系数作为初始扰动,在此基础上引入频率正反馈,只要扰动产生相位角偏移的速度比负载阻抗角变化的速度快,孤岛检测就一定可以成功。在实际应用中,由于系统存在很多非线性因素,即便没有初始扰动,频率差也会存在,但由于频差的方向与负载阻抗角方向不同,孤岛检测时间变长甚至检测失败;在品质因数较大情况下,负载阻抗角的变化速度快,需要的正反馈系数尽可能较大,但正反馈系数太大又会影响逆变器的电能质量。因此,在实际并网逆变器中,AFDPF检测技术正反馈系数的设置会同时受到电能质量和孤岛检测准确度的制约。

3　AFDLIA孤岛检测技术

3.1　AFDPF孤岛检测技术的机理

本文第1节中提到AFD检测技术的机理是将轻微失真的逆变器电流注入电网,决定该失真电流电网故障时引起公共点电压发生频率偏移量大小的是截断系数cf值,cf=ωtz/π。为了加快主动频移的速度,文献[14]提出了AFDPF检测技术,采用式(12)所示的正反馈控制,逆变器电流给定的扰动截断系数随着频率的偏移而递增。即

cf=cf0+k(f-fg)

(12)

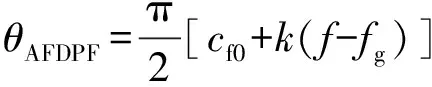
(13)

式中:θAFDPF为AFDPF检测结束的移频相角;cf0为初始截断系数;k为正反馈系数;f为公共点电压实时频率;fg为电网电压标准频率。

3.2　AFDLIA孤岛检测技术的实现

AFD检测技术和AFDPF孤岛检测技术的参数是固定的,而负载特性是多种多样的,多逆变器的情况下彼此之间的扰动也存在不同[19]。因此,基于附录A图A1(a)所示的带负载电流传感器的并/离网逆变器模型,本文提出了一种AFDLIA孤岛检测技术。该并/离网逆变器主要有三种运行模式:①离网带负载运行模式;②逆变器不运行,电网带负载;③逆变器并网带负载运行,文中以第3种并网带负载情况讨论孤岛保护。AFDLIA检测技术是一种改进型AFDPF检测技术,其截断系数随负载阻抗角的变化而自适应调节,不再为常数。

在孤岛检测中,当负载阻抗角较小时,截断系数的初始扰动值cf0越大,越有利于公共点电压频率发生偏移,但cf0太大会影响到逆变器的电能质量。因此,本文会以谐波畸变率小为前提设置截断系数的初始扰动cf0。首先,对负载电流Iload进行锁相,得到负载阻抗角θload。

1)初始扰动cf0的设计

对于初始扰动系数的定义为:

cfk0=-kcfcfmaxsign(θload)

(14)

式中:cfmax为在负载阻抗角为零时的一个固定扰动,根据谐波畸变率的要求,一般将之设定为0.01;sign(·)为取正负值函数，若θload数值为正，则函数值为1，若为负，则函数值为-1。kcf为一个随着θload绝对值变化的自适应变量。即

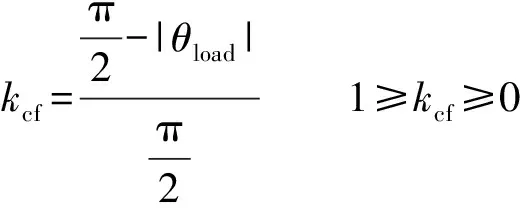
(15)

由于实际应用中负载的阻抗角在[-π/2,π/2]之间,因此随着负载阻抗角的减小cfk0会逐渐增大,但由前一个公式可以看出最大也不会超过0.01,因此在正常并网的情况下谐波畸变率得到了保证。cfk0的扰动方向与负载阻抗角对公共点电压频率作用的方向一致,不论在何种情况下,该初始扰动都能够使得公共点电压频率发生偏移。

2)负载反馈截断系数的设计

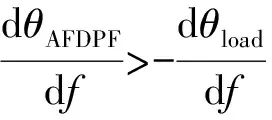
由负载频率特性可知,在电网电压基准频率发生谐振的负载最容易导致孤岛检测失败,电网频率下其负载阻抗角为零。在电网发生故障的情况下,如果AFD扰动使得公共点电压频移的速度大于阻抗角变化产生的频移速度,系统一定能够成功地检测孤岛并实施保护或切换离网模式。因此,要消除AFDPF检测技术的检测盲区,那么必须满足以下条件。即

(16)

对式(13)求导,可得:

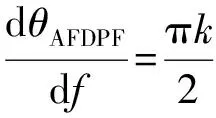
(17)

要满足公式(16)中的条件,那么k满足的条件为:

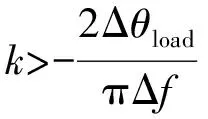
(18)

当负载的谐振频率与电网频率相同,在并网的时候,Δθload和Δf都是零,不利于在微控制器中计算。在电网发生故障时刻,负载阻抗角和公共点电压频率的变化为:

Δθload=θload,k-θload,k-1

(19)

Δf=fk-fk-1

(20)

由式(9)推导出负载阻抗角随频率变化趋势为:

(21)

其变化趋势由负载自身特性所决定。因此,在电网发生故障时刻负载阻抗角变化的斜率是一定的,即

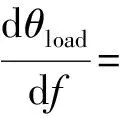
(22)

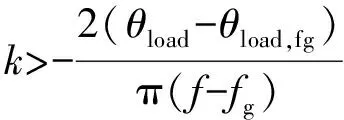
(23)

式中:θload为系统实时采样负载阻抗角;f为公共点电压实时频率;fg为电网电压频率;θload,fg为并网时刻的负载阻抗角。

主动频移检测方法的截断系数满足的关系为:

(24)

对于本文所提出的AFDLIA检测方法,可将截断系数设为:

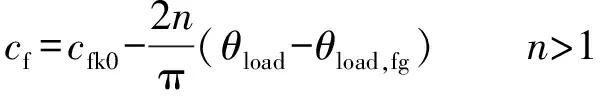
(25)

由式(25)可知,截断系数cf的设置与负载阻抗角相关;系数n的调节可以改变孤岛检测的时间。在并网时刻θload-θload,fg的值为零,cf最大是0.01,因此可以保证并网电流的电能质量。

由式(18)可知,当AFDPF检测技术不满足k>-2Δθload/(πΔf)时,孤岛检测落入检测盲区,检测失败。将式(25)写成AFDPF检测技术的形式。即

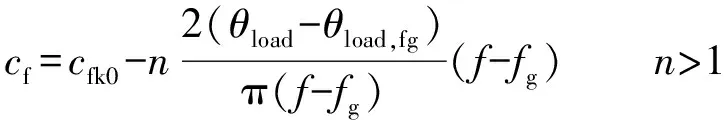
(26)

式中:由于n是一个始终大于1的数,正反馈系数始终满足k>-2Δθload/(πΔf)的条件,如式(27)所示。

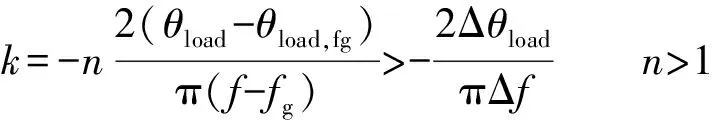
(27)

因此,只要n>1,本文所提的AFDLIA孤岛检测技术不论何种恶劣的负载条件下均不存在检测盲区。

3.3　多逆变器并网发电系统的AFDLIA孤岛检测

多台逆变器运行时,逆变器之间会发生稀释现象[19]。附录A图A2(b)所示为两台并/离网逆变器构成的多逆变器系统模型示意图,值得一提的是,并/离网逆变器的负载电流信息是通过逆变器装置内部的电流传感器获得的,因此附录A图A1(b)中将两台逆变器并联连接等效负载是为了方便分析和设置负载的参数。当逆变器1采用AFD检测技术向上频率偏移,而逆变器2采用AFD检测技术向下频率偏移,若偏移量相等,那么电网故障时,两个逆变器公共点电压均不发生频率偏移。采用AFDPF检测技术,初始扰动产生的稀释影响与AFD检测技术相同,同时还存在频差检测误差带来的稀释现象。

而本文提出的AFDLIA检测技术,其初始扰动方向与负载阻抗角方向一致,在负载阻抗角变化为零时,主要由初始扰动cfk0和负载阻抗角同时作用使公共点电压频率发生偏移,因此可以忽略频率检测误差带来的影响。由于cf=ωtz/π,当两台逆变器系统同时采用AFDLIA检测技术,可表示为:

Iref1(t)=

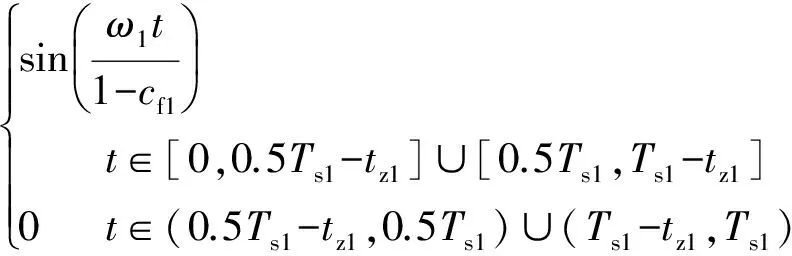
(28)

Iref2(t)=

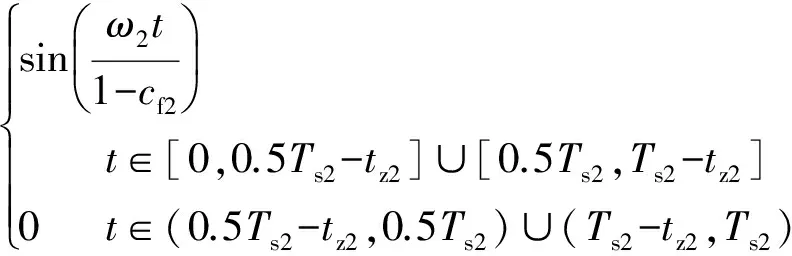
(29)

式中:cf=2tz/Ts;Iref1和Iref2分别为两台归一化的逆变器输出电流参考值;cf1和cf2是两台逆变器对应的斩波系数。

两台逆变器的作用等效成一台逆变器为:

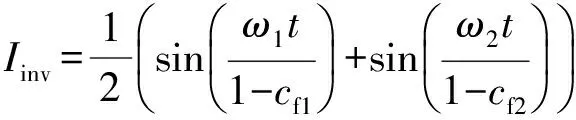
(30)

两台逆变器的参考电流的频率都为电网电压的频率,因此忽略他们之间的频率误差,ω1=ω2=ω,式(28)等效为:

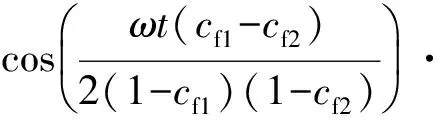
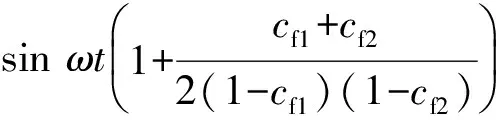
(31)

由于θ1与θ2较小,式(29)可以等价为:

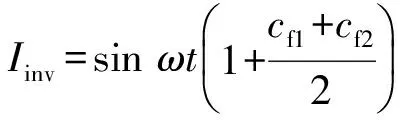
(32)

当cf1与cf2符号相同时,移相角为0.5ωt(cf1+cf2),移相角等于两台逆变器的平均值;当cf1与cf2符号相反时,移相角为0.5ωt(|cf1|+|cf2|),两台逆变器的移相角相抵消,移相作用减弱。

若两台逆变器均采用本文所提的AFDLIA检测技术,其移相角可表示为:

θAFDLIA=0.5ωt(cf1+cf2)=

(33)

式中:n1和n2大于1,两台逆变器均采用AFDLIA检测技术,其等效截断系数为两台逆变器的均值;初始扰动为(cfk01+cfk02)/2,不会发生稀释效应。

3.4　系统非线性因素分析

在实际的并/离网双模式光伏发电系统中,存在很多由非线性因素产生的误差:①通过锁相环得到的负载阻抗角存在一定的误差;②电压电流传感器经过数字锁相环得到的频率存在一定程度的误差。这些误差跟数字处理器的速度密切相关。因此,需要对3.1节中的孤岛检测技术作相应的分段式处理。

首先,当负载阻抗角在接近零的很小范围内变化时,由于通过锁相环得到的负载阻抗角存在一定的误差和延时,此时的正负值存在不确定性。那么初始扰动会一直处于一种震荡的状态,使得检测时间加长甚至导致失败。因此,可以将初始扰动设定为一个确定值,本文将cfk0定义为:

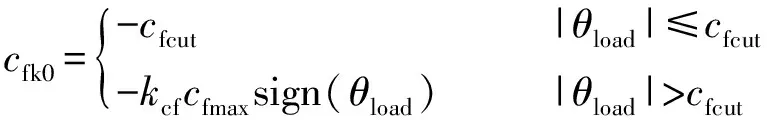
(34)

因此本文将负载阻抗角接近零时定义为-cfcut,-cfcut可以根据实际系统中负载阻抗角检测精度的容忍度来调节。值得一提的,初始系数的分段是为了避免采样误差带来的扰动震荡问题,当孤岛发生-cfcut使公共点电压频率发生微小偏移后,便由负载阻抗角的反馈值产生频率偏移扰动。因此,为了保证并网的电能质量,-cfcut不宜设置得太大。

其次,在实际系统中,系数n将放大并网时负载阻抗角的检测误差并附加给扰动,降低了逆变器的输出电能质量。为此,本文以频率的阈值为界限,当频差较小时,本文采用类比基于三次幂的检测方法,减小系数n的影响;当频差较大时,采用类比于基于抛物线的检测方法[13],增强系数n的移频作用。即

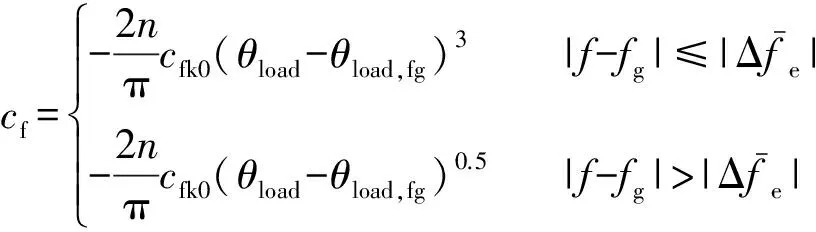
(35)

4　仿真与实验

1)仿真结果与分析

本文采用MATLAB/Simulink对所提方法进行仿真验证。单台逆变器的模型如附录A图A1(a)所示,相关参数如下:电网电压有效值和频率分别为220 V,50 Hz;逆变器直流侧电压为360 V,采用单位功率因数的电流控制方式,逆变器输出电流有效值为9.09 A,逆变器输出端滤波电感为1.5 mH;本地负载为RLC并联负载,额定电压为220 V,频率为50 Hz,负载吸收有功功率为2 kW,负载电阻值为24.2 Ω,仿真中-cfcut取-0.001,仿真结果中Ug为公共点电压,Iinv为输出电流,频率阈值为49.5 Hz。

在不同品质因数的负载条件下,本文对传统的AFDPF检测技术和AFDLIA检测技术做了对比,RLC并联负载谐振频率为50 Hz,R=24.2 Ω。图3(a)为AFDPF检测技术,正反馈系数为0.1,初始截断系数cf0为-0.01,负载品质因数为2.5,电网故障89 ms后公共点电压频率超过阈值49.5 Hz,孤岛检测成功并实施孤岛保护。图3(b)为正反馈系数为0.1,初始截断系数cf0为-0.01的AFDPF检测技术,负载品质因数为6.0,公共点电压频率在到达49.8 Hz之后就进入稳态,孤岛检测失败。

AFDLIA检测技术中n=2,图3(c)为负载品质因数为2.5的仿真结果,图3(d)为负载品质因数为6.0的仿真结果。两种负载情况下,电网故障102 ms后公共点电压频率均超过阈值49.5 Hz,孤岛检测成功并实施孤岛保护。从仿真结果图3(a),(b)表明,AFDPF检测技术受到负载品质因数的影响较大,根据正反馈系数的不同其存在的盲区范围也不同,因此固定的正反馈系数使得检测技术总是存在盲区。仿真结果图3(c),(d)证明了本文提出AFDLIA孤岛检测算法中的截断系数随负载相位角的变化而变化,检测精度不受负载品质因数的影响,消除了孤岛检测的盲区。

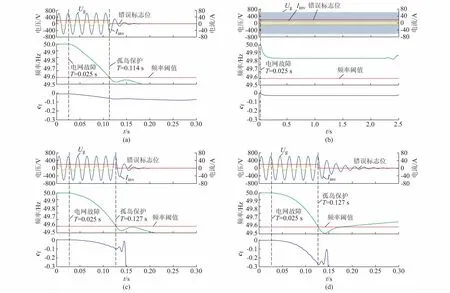
图3　单台逆变器孤岛检测仿真图Fig.3　Simulation results of a single inverter with AFDPF islanding detection technology

关于AFDLIA检测技术中n的设置,通过表1中不同负载品质因数的孤岛检测时间表分析可知,n值的大小一般只影响孤岛检测的时间,跟负载品质因数的大小无关。根据国标GB/T 19939—2005中所提出的在2 s内检测出孤岛的时间要求,为控制孤岛检测时间在100 ms以内,本文中提出的AFDLIA检测技术中n值可采用2.5。

表1　AFDLIA孤岛检测方法检测时间Table 1　Time of AFDLIA islanding detection technology

2)实验结果与分析

为进一步验证所提孤岛检测算法的有效性,在一台3 kW的并/离网双模式逆变器上进行了实验验证,实验平台见附录A图A2。实验参数为:电网电压有效值为220 V、频率为50 Hz,逆变器单位功率因数运行。RLC并联负载采用群菱公司ACLT-3803H防孤岛试验检测装置。附录A图A3为本文所提方法的实验验证,图中红色波形是孤岛检测装置断路器两端电压波形,正常并网时Upcc-Ug=0;模拟电网故障断路器断开,Upcc发生偏移直到孤岛检测成功,Upcc被负载钳位至地电位,Upcc-Ug=-Ug;蓝色波形是逆变器输出电流的波形。

采用本文所提AFDLIA检测技术,n值设为2.5,附录A图A3(a)中负载品质因数为2.5,孤岛检测时间为91 ms;附录A图A3(b)中负载品质因数为6.0,孤岛检测时间为95 ms。实验结果表明,AFDLIA检测技术注入电流的扰动随负载相位角的变化而变化,不受负载品质因数的影响,无检测盲区。该实验结果与仿真结果一致,验证了本文所提基于负载阻抗角的主动频移孤岛检测技术的有效性。

为了验证本文对AFDLIA检测技术的截断系数做分段式处理的有效性,在实验中对比了采用AFDPF和AFDLIA两种孤岛检测技术的逆变器在正常并网时输出电流的谐波畸变率。附录A图A4(a),(b)分别为采用AFDLIA和AFDPF孤岛检测技术并网时的实验波形,上半部分为TektronifxDPO3014数字示波器波形图,下半部分为HIOKI3390功率分析仪的并网电流总谐波畸变率(THD)分析。附录A图A4(a)中的电流的THD为2.74%,附录A图A4(b)中的电流的THD为5.45%,而实际工作中存在诸多非线性因素,在不注入孤岛扰动情况下的并网电流的THD为2.35%。从表2中可以看出在正常并网时,采用AFDPF检测技术的逆变器并网电流的THD随着正反馈系数的增加而递增。然而,采用AFDLIA检测技术的逆变器并网电流的THD却基本不变。说明在实际的逆变器系统当中将AFDLIA孤岛检测技术截断系数做分段式处理可以很好地保证并网模式的电能质量。

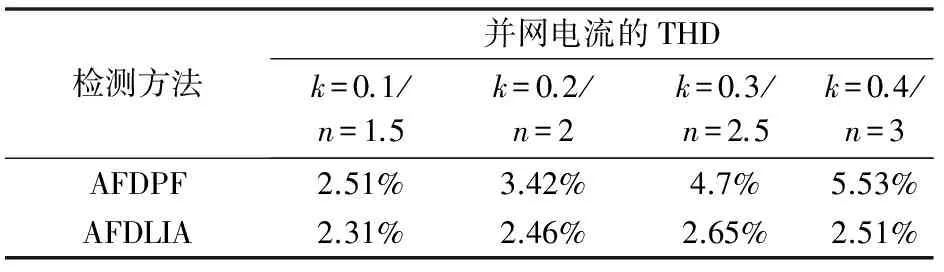
表2　AFDPF和AFDLIA检测方法并网电流THD比较Table 2　THD comparison between AFDPF and AFDLIA algorithm

3)多逆变器系统仿真结果与分析

两台逆变器的模型如附录A图A1(b)所示,电网参数与单台逆变器相同,输出电流有效值均为4.045 A,逆变器输出端滤波电感为1.5 mH;本地负载为RLC并联负载,品质因数Qf=2.5,R=24.2 Ω,L=0.308 mH,C=328.83 μF,负载吸收有功功率均为2 kW,负载电阻值为24.2 Ω。

仿真结果如图4所示,图中电网故障发生在0.05 s。图4(a)逆变器1采用AFD检测技术扰动向下,cf=-0.04,逆变器2采用AFD检测技术扰动下上cf=0.04,结果显示电网故障后多逆变器系统孤岛检测发生稀释现象,孤岛检测失败,单台逆变器cf0=0.04的AFD检测技术会在电网故障84 ms后检测成功。图4(b)中逆变器1采用AFDPF检测技术,初始扰动cf0=-0.01,正反馈系数k=0.15逆变器2采用AFDPF检测技术,其中初始扰动cf0=0.01,正反馈系数k=0.15,结果显示电网故障后多逆变器系统在129 ms之后检测出孤岛,与该负载条件下单台逆变器采用AFDPF检测技术相比,检测时间增加了46 ms,稀释现象较严重。图4(c)逆变器1和逆变器2均采用AFDLIA检测技术,cfmax为0.01,n值取2.5,结果显示电网故障后多逆变器系统在89 ms之后检测出孤岛,与该负载条件下单台逆变器采用AFDLIA检测技术的检测时间相同。综上所述,本文提出的AFDLIA检测技术在多逆变器情况下不存在稀释现象。

5　总结

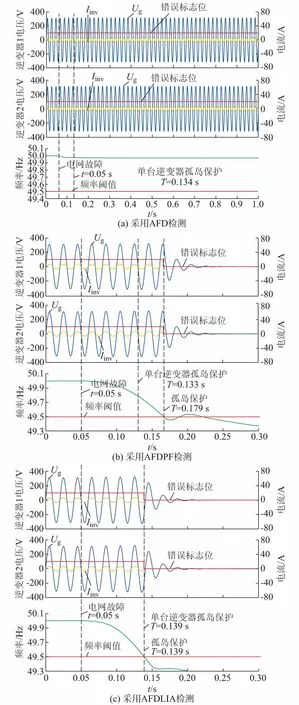
图4　多逆变器的孤岛检测仿真结果图Fig.4　Simulation result of islanding detection in multi-inverters

随着户用式光伏发电系统的发展与应用,用户负载要求光伏发电装置具有不间断供电的能力,本文基于传统主动式孤岛检测技术,以并/离网逆变器为研究对象,将负载阻抗角信息作为一个可知量,提出了一种AFDLIA孤岛检测方法。根据负载阻抗角的变化,实时地调整注入电流扰动的大小,提高了孤岛检测的准确性。为减小系统非线性因素的影响,对所提方法进行改进,提高了系统的并网电能质量。

本文所提AFDLIA孤岛检测方法解决了传统主动式孤岛检测技术准确性与系统并网电能质量之间的矛盾,完全消除了检测盲区,但没有彻底解决孤岛检测带来的电流畸变问题。这将成为分布式发电并网系统中本地孤岛检测技术的下一个研究方向。

本文研究获得中南大学2017年研究生自主探索创新项目(2017zzts489)资助,特此致谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] STEVENS J. Utility intertied photovoltaic system islanding experiments[C]// Proceedings of the 17th IEEE Photovoltaic Specialists Conference, May 4, 1987, New Orleans, LA, USA: 1134-1138.

[2] GUO X, LIU W, LU Z. Flexible power regulation and current-limited control of grid-connected inverter under unbalanced grid voltage faults[J]. IEEE Transactions on industrial Electronics, 2017, 64(9): 7425-7432.

[3] BOWER W, ROPP M. Evaluation of islanding detection methods for photovoltaic utility-interactive power systems[R]. Albuquerque, USA: Sandia National Labs, 2002.

[4] 程启明,王映菲,程尹曼,等.分布式发电并网系统中孤岛检测方法的综述研究[J].电力系统保护与控制,2011,39(6):147-154.

CHENG Qiming, WANG Yingfei, CHENG Yinman, et al. Overview study on islanding detecting methods for distributed generation grid-connected system [J]. Power System Protection and Control, 2011, 39(6): 147-154.

[5] 鹿婷.太阳能光伏系统并网及其孤岛检测[D].武汉:华中科技大学,2006.

[6] 蔡逢煌,王武,陈四雄,等.一种改进的主动移频式孤岛检测技术[J].电力系统保护与控制,2013,41(24):70-75.

CAI Fenghuang, WANG Wu, CHEN Sixiong, et al. An improved active frequency drift islanding detection[J]. Power System Protection and Control, 2013, 41(24): 70-75.

[7] 蒋翠,祁新梅,郑寿森.带电压频率正反馈的主动移频式孤岛检测方法[J].电力系统保护与控制,2014,42(8):95-100.

JIANG Cui, QI Xinmei, ZHENG Shousen. Active frequency drift islanding detection with positive feedback of voltage frequency[J]. Power System Protection and Control, 2014, 42(8): 95-100.

[8] 张学广,王瑞,刘新龙,等.改进的主动频率偏移孤岛检测算法[J].电力系统自动化,2012,36(14):200-209.

ZHANG Xueguang, WANG Rui, LIU Xinlong, et al. Improved active frequency drift anti-islanding algorithm[J]. Automation of Electric Power Systems, 2012, 36(14): 200-209.

[9] 刘新天,冯嘉骏,何耀,等.基于闭环锁频控制的并网逆变器孤岛检测方法[J].电力系统自动化,2017,41(22):116-123.DOI:10.7500/AEPS20170524002.

LIU Xintian, FENG Jiajun, HE Yao, et al. Islanding detection method based on closed-loop frequecy-locked control for grid-connected inverters[J]. Automation of Electric Power Systems, 2017, 41(22): 116-123. DOI: 10.7500/AEPS20170524002.

[10] GUPTA P, BHATIA R S, JAIN D K. Average absolute frequency deviation value based active islanding detection technique[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 26-35.

[11] 李瑞生,郭宝甫,曾正.低频电源注入式主动孤岛检测方案[J].电力系统自动化,2017,41(5):114-120.DOI:10.7500/AEPS20160413007.

LI Ruisheng, GUO Baofu, ZENG Zheng. Active islanding detection scheme based on low frequency power supply injection[J]. Automation of Electric Power Systems, 2014, 41(5): 114-120. DOI: 10.7500/AEPS20160413007.

[12] PANKAJ G, BHATIA R S. Active ROCOF relay for islanding detection[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 420-429.

[13] 丁浩,何宇,漆汉宏,等.基于抛物线型SMS算法的孤岛检测[J].电工技术学报,2013,28(10):233-240.

DING Hao, HE Yu, QI Hanhong, et al. Islanding detection based on parabolic SMS algorithm[J]. Transactions of China Electro technical Society, 2013, 28(10): 233-240.

[14] ROPP M E, BEGOVIC M, ROHATGI A. Analysis and performance assessment of the active frequency drift method of islanding prevention[J]. IEEE Transaction on Energy Conversion, 1999, 14(3): 810-816.

[15] IEEE recommended practice for utility interface of photovoltaic (PV) systems: IEEE Std 929—2000[S]. 2000.

[16] 中国国家标准化管理委员会.光伏系统并网技术要求:GB/T 19939—2005[S].北京:中国标准出版社,2005.

[17] 吴波,郭育华,文宇良.单相电力锁相环的改进和FPGA实现[J].电力电子技术,2008,42(4):80-82.

WU Bo, GUO Yuhua, WEN Yuliang. Improvement of single phase power phase locked loop and FPGA implementation[J]. Power Electronic Technology, 2008, 42(4): 80-82.

[18] 刘芙蓉.并网型户用光伏系统的孤岛检测技术研究[D].武汉:华中科技大学,2008.

[19] LOPES L, ZHANG Yongzheng. Islanding detection assessment of multi-inverter systems with active frequency drift methods[J]. IEEE Transactions on Power Delivery, 2008, 23(1): 480-486.

唐忠廷(1990—),女,博士研究生,主要研究方向:电力电子装置及太阳能发电技术。E-mail： tinatcsu@163.com

粟梅(1967—),女,教授,主要研究方向:新能源发电、现代电力电子系统建模与控制。E-mail: sumeicsu@mail.csu.edu.cn

刘尧(1988—),男,硕士研究生,主要研究方向:电力电子、微电网控制技术。E-mail: yaoliu@csu.edu.cn

王辉(1984—),男,通信作者,讲师,主要研究方向:电力电子装置及其建模与控制技术。E-mail: wanghuicp9@csu.edu.cn