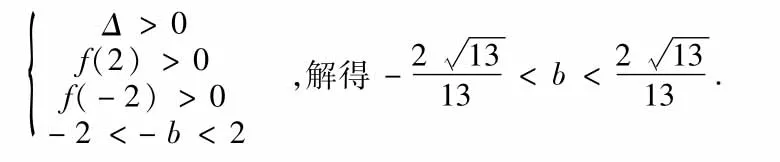熟知知识背景 揭示问题实质——多角度例说圆锥曲线中的一类对称问题

◎姚石

角度1 根据判别式及韦达定理来求解

假设两点A、B关于直线l对称，根据两点关于一条直线对称的知识背景，首先要明确对称中体现的两要点：垂直和两点连线中点在对称直线l上，因此使用这种方法求解时，必须同时确保：⑴垂直；⑵平分⑶存在，下面就说明三个确保的实施。解法如下：设椭圆上存在A、B两点关于直线对称，为了保证A、B两点所在的直线与直线l垂直，故设直线AB为：则直线 AB与椭圆有两个不同的交点，即，得：13x2－8nx＋16n2－48＝0⇒Δ＝－192（4b2－13）＞0，解得设点 A（x1，y1）、B（x2，y2），由韦达定理得：，所以A、B两点中点的横坐标为纵坐标为，因此点在直线直线l：4x－y＋b＝0上，即：，解出所以可得：

角度2 根据点差法的知识背景来求解

点差法是解决中点弦的一种常见解题方法，在已知弦中点坐标的前提下，能快速得到弦所在直线的斜率问题，而该题目完全符合点差法的应用条件，解题过程如下：设椭圆上关于直线 l对称的两点 A（x1，y1）、B（x2，y2），弦 AB的中点为 M（x0，y0），利用点差法得：在直线l：4x－y＋b＝0上，得：y0＝4x0＋b···② ，①②联立得到x0＝－b，y0＝－3b，因为点M（x0，y0）在椭圆内部，即

角度3 根据平行弦中点轨迹的背景来求解

根据有关弦中点轨迹的思路，可以通过轨迹曲线与圆锥曲线的位置关系，可利用数形结合寻找参数范围。解题思路如下：

设椭圆上关于直线l对称的两点 A（x1，y1）、B（x2，y2），弦 AB的中点为 M（x0，y0），利用点差法得：，得y0＝3x0，所以以为斜率的平行弦的中点轨迹是直线y＝3x在椭圆内部的一段（不包括端点）。将y＝3x与椭圆联立得两交点，所以问题即转化为直线l：4xy＋b＝0与线段有交点，易得

角度4 根据根的分布来求解

椭圆上存在不同两点关于直线l对称，等价于椭圆上存在被l垂直平分弦，即等价于椭圆的适合条件的弦所在的直线方程，与曲线的方程组成的方程组在某确定的区间上有两个不同的解，因此可以利用一元二次方程根的分布来解，解题过程如下：根据角度2得到中点M（x0，y0）的坐标为（－b，－3b），直线AB的方程为：