从错误剖析到概念清晰

◎林少云

概率是新教材的一个重要内容，在每年高考中都占有一席之地。但是由于这部分内容的概念比较多，相近概念容易混淆，在解题过程中，学生会经常出现一些表面看起来正确而实际上是错误的解法。笔者认为，在教学过程中如果能及时向学生剖析造成错解的原因，可以帮助学生更加透彻地理解这些概念，提高他们的辨别能力，减少错解的发生。下面就学生在解题中经常混淆的概念进行剖析。

一、“概率”和“频率”

例1：把一枚质地均匀的硬币连续掷1000次，其中有496次正面朝上，504次反面朝上，则可认为掷一次硬币正面朝上的概率为______。

所以掷一次硬币正面朝上的概率为0．496。

剖析：错误的原因是混淆了概率和频率的概念，事实上频率是随机的，做同样的试验得到的频率可能是不同的，如本题中的0．496是1000次试验中硬币正面朝上的频率；而概率是一个确定的常数，是客观存在的，与试验次数无关。

正解：通过做大量的试验可以发现，硬币正面朝上的频率都在0．5附近摆动并趋于稳定，故掷一次硬币，正面朝上的概率为0．5。

点评：学生在小学时对事件发生的可能性的大小已经有了初步的认识，可以从试验中归纳、总结得到一个事件发生的频率，进而可能就认为这个频率就是这个事件发生的概率，通过该错解，让学生区别两者的不同：频率是随机的，概率是确定的，随着实验次数的增加，频率在概率附近摆动。

二、“非等可能”和“等可能”［1］

例1（古典概型）：先后抛掷两枚质地均匀的硬币，求出现“一枚正面朝上，一枚反面朝上”的概率。

错解：先后抛掷两枚质地均匀的硬币，有（正，正）、（正，反）、（反，反）共3种结果，所以

剖析：错误的原因是以上3种结果不是等可能发生的，（正，反）包括（正，反）和

（反，正）两种不同的情况，从而得出错误的概率。

正解：先后抛掷两枚质地均匀的硬币，有（正，正）、（正，反）、（反，正）、

例2（几何概型）：在等腰RtΔABC中，过直角顶点C在∠ACB内部任作一条射线CM与线段AB交于点M，求AM ＜AC的概率。［1］［2］

错解：由于点M随机地落在线段AB上，故可以认为点M落在线段AB上任一点是等可能的，可以将长度作为测度。在线段

AB上截取AC＇＝AC＇。当点M位于线段AC＇上时，AM＜AC

剖析：该解法错误的原因也是不满足等可能性。证明如下：以C为圆心，AC为半径作四分之一圆，H为弧AB的中点，连结CH交AB于G，取弧AH的中点Q，连结CQ交AG于P，连结PH，则CH⊥AB，∠ACQ＝∠HCQ．又CA＝CH，CP＝CP，所以ΔHPC≅ΔAPC，所以AP＝HP．在RtΔGHP中，HP＞GP，所以AP＞GP．也就是说当射线CM在∠ACB内部均匀分布时，所对应的点M在线段AB上却不是均匀分布的。

正解：在∠ACB内的射线CM是均匀分布的，所以射线CM在任何位置都是等可能的，在AB上取AC／＝AC，则∠ACC／＝67．5°，故满足条件的概率为

三、“有序”和“无序”

例1、从5名乒乓球队员中选3人参加团体比赛，其中甲在乙前出场的概率为（ ）

剖析：题中“甲在乙前出场”已经暗示了此题应作为有序问题处理，所以此解法错误的原因是把有序当无序。

例2：从10件产品（其中次品3件）中，一件一件地不放回地任意取出4件，求4件中恰有1件次品的概率。错解：从10件取4件共有种取法，设A＝“取出的4件中恰有1件次品”，则A含有种结果，所以

剖析：在处理概率问题时，有些问题可以按“有序”处理，也可按“无序”处理，但处理时必须保证分子和分母的统一性。而该错解计算事件A所含基本事件的个数是用组合的方法，即没有考虑抽取的顺序；而计算基本事件的总数时是用排列的方法，即考虑了抽取的顺序。

ADAMS软件使用交互式图形环境和零件库、约束库以及力库创建完全参数化的机械系统几何模型，其求解器采用多刚体系统力学理论中的拉格朗日方程方法，建立系统动力学方程，对虚拟机械系统进行动力学分析，输出位移、位置等所需要的数据曲线[1]。

正解：（1）都用排列方法

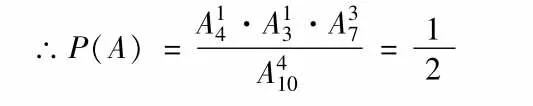
（2）都用组合方法

一件一件不放回地抽取4件，可以看成一次抽取4件，总共含有个基本事件，A包含有个基本事件。

点评：碰到抽取问题时，首先要认真审题，确定是“有序问题”还是“无序问题”，如果是可有可无的顺序问题，在实际处理时，必须保证分子和分母的统一性

四、“互斥”和“对立”

例：从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两事件是（ ）

A．至少有1个白球与都是白球 B．至少有1个白球与至少有1个红球

C．至少有1个白球与都是红球 D．恰有1个白球与恰有2个红球

错解：C

剖析：本题错误在于把“互斥”与“对立”混同，要准确解答这类问题，必须搞清对立事件与互斥事件的联系与区别：

（1）两事件对立，必定互斥，但互斥未必对立；

（2）互斥的概念适用于多个事件，但对立概念只适用于两个事件；

（3）两个事件互斥只表明这两个事件不能同时发生，即至多只能发生其中一个，但可以都不发生；而两事件对立则表示它们有且仅有一个发生。

正解：事件“甲分得红牌”与“乙分得红牌”是不能同时发生的两个事件，这两个事件可能恰有一个发生，也可能两个都不发生，所以应选C。

点评：该错解除了让学生搞清对立事件与互斥事件的联系与区别之外，也让他们知道判断两事件的关系，应先判断两者是否互斥，若不互斥，则肯定也不对立；若互斥，则进一步判断它们是否对立。

五、“互斥”和“相互独立”

例：甲投篮命中率为0．8，乙投篮命中率为0．7，每人投3次，两人恰好都命中2次的概率是多少？

错解：设“甲恰好投中两次”为事件A，“乙恰好投中两次”为事件B，

剖析：本题错误原因是把相互独立同时发生的事件当成了互斥事件。

正解：设“甲恰好投中两次”为事件A，“乙恰好投中两次”为事件B，且A，B相互独立，则两人都恰好投中两次为事件A×B，于是P（A×

点评：“互斥”和“相互独立”是不同的概念，互斥事件是指同一试验下的两个事件不可能同时发生；两事件相互独立是指一个事件的发生与否对另一个事件发生与否没有影响，这两个事件事件是两次或更多次不同试验下出现的，它们虽然都描绘了两个事件间的关系，但所描绘的关系是根本不同的。而且两者的概率公式也不同：若A、B为互斥事件，则P（A＋B）＝P（A）＋P（B）；若A、B相互独立，则P（AB）＝P（A）P（B）。

六、“条件概率”与“积事件的概率”［2］

例1、100件产品中有10件次品，随机不放回取两次，每次取一件，求在第一次取得正品的条件下，第二次取得正品的概率．

错解：设第一次取得正品为事件A，第二次取得正品为事件B，则在第一次取得正品的条件下，第二次取得正品为事件AB，所以所求的概率为

剖析：解题的错误是由于对条件概率的定义理解不深刻，“第一次取得正品后第二次又取得正品的概率”与“在第一次取得正品的条件下，第二次取得正品的概率”的意义是不相同的，前者是积事件的概率，而后者的意思是在第一次取得正品已经预先发生的条件下，再来进行第二次试验而取得正品的条件概率．

例2、袋中有6个黄色、4个白色的乒乓球，作不放回抽样，每次任取一球，取2次，求第二次才取到黄色球的概率．

错解：记“第一次取到白球”为事件A，“第二次取到黄球”为事件B，“第二次才取到黄球”为事件C，则

剖析：本题错误也是在于对积事件的概率与条件概率的含义没有弄清，对“第二次才取到黄球”这一事件，并不是“第一次取到白球”已经预先发生，而是与“第二次取到黄球”同时发生，所以它不是条件概率而是积事件的概率．

正解：第二次才取到黄球的概率为 P（C）＝P（AB）＝P（A）·

点评：条件概率与积事件概率本来是意义非常明确的两个不同概念，但是初学者在一些稍复杂一点的问题中却往往将这两种概率张冠李戴，导致错误的结果．对此，笔者在多年的教学中感到这是概率中解题差错率较高的部分，应予足够的重视。事实上，设是随机试验对应的样本空间Ω中的两个事件。必须注意：P（A1A2）是A1，A2同时发生的概率，而是在A已经发生的条件下，A2发生的概率。从样本空间的角度来看，这两种事件所对应的样本空间发生了改变，求P（A1A2）时，我们仍在原来的随机试验所对应的样本空间Ω进行讨论；求时，所考虑的样本空间就不是Ω了，这是因为前提条件中已经知道了一个条件（即A1已发生）。这样所考虑的样本空间的范围必然缩小了。因此。事件“A1A2”与事件“”是两种截然不同的事件，但它们也不是一点联系都没有，乘法公式就给出了这两种事件概率之间的联系。

通过对上述问题的错解剖析，可以看到概念在解题中有着不可忽视的作用，这就要求教师自身要加强概率中概念的学习和反思，真正的将抽象的概率知识转化为具体的概念知识。同时在教学中，要善于利用教材中的典型例题，让学生能看到一般概念的实际背景，弄清知识的来龙去脉，将不同概念区别开来。［3］［4］

参考文献：

［1］彭锦平．高中立体几何解题教学研究与实践．［J］湖南师范大学．2015－06－01

［2］星汉．高中概率题中的数学思想方法运用［J］科学大众（科学教育）．2017－02－20

［3］顾泽多．数学教学过程中解题思路初探研究［J］教育现代化．2017－12－11

［4］曾剑明．高中数学教学中培养学生主体参与意识的教学策略［J］教育现代化．2017－12－11